正弦波供电下永磁同步电动机径向电磁力波研究

韩雪岩， 李生祥， 米秀峰

(沈阳工业大学国家稀土永磁电机工程技术研究中心， 辽宁 沈阳 110870)

正弦波供电下永磁同步电动机径向电磁力波研究

韩雪岩， 李生祥， 米秀峰

(沈阳工业大学国家稀土永磁电机工程技术研究中心， 辽宁 沈阳 110870)

径向电磁力是影响永磁同步电动机电磁振动噪声的主要原因。抑制永磁电机电磁振动噪声的方法为：①提高电磁力波次数；②降低电磁力波幅值；③使电磁力波频率远离电机的固有频率。本文分析了永磁同步电动机的径向电磁力波次数和频率，对力波次数以及不同磁场产生的力波频率所满足的规律进行了总结；并使用有限元法计算了两台电机的气隙磁场谐波，对由气隙磁场产生的低次数径向力波幅值进行分析，找出了产生低次数大幅值径向力波的磁场谐波源规律。

振动噪声； 电磁力波； 永磁同步电机； 单边磁拉力

1 引言

永磁电机由于结构简单、运行可靠、功率密度高和损耗低等诸多优点被广泛应用[1]。但是，永磁电机谐波含量高，振动噪声偏大，其振动噪声特性已成为近年来的研究热点。国内外很多学者对永磁电机的振动噪声做了研究。2009年，诸自强教授使用解析法和有限元法对分数槽永磁无刷直流电机的径向电磁力进行了研究，并详细分析了空载和负载条件下的气隙磁场以及极槽配合、绕组单双层等对电磁力波的影响[2,3]，文中指出开槽对电枢反应磁场的影响较小。2009年，G. Dajaku等学者详细研究了10极12槽表贴式永磁电机的电磁力波，指出2次力波对该电机振动噪声的影响最大[4]。2009至2010年，山东大学张冉对表面式永磁电机的电磁力波做了研究，提出了通过磁极偏心、开辅助槽、合理选择极弧系数等方法来削弱空载条件下永磁电机的激振力[5-8]。2010年，H.C.M. Mai等学者对比分析了28极30槽、28极42槽、28极84槽等极槽配合对电机谐振的影响[9]。2010年，沈阳工业大学宋志环博士推导了正弦波供电和变频器供电条件下永磁电机径向电磁力的解析表达式[10]。2011年，浙江大学杨浩东等研究了6种常用极槽配合电机的电磁振动，指出整数槽电机定子内径上的电磁力谐波的主要分量为2倍的电频率，其模数等于电机的极数，而分数槽电机则会出现低模数的电磁振动[11]。

文献[4-11]将电磁力波做高、低次的区分，重点分析了不同极槽配合下可能出现的电磁力波次数。本文在此基础上，进一步对低次数电磁力波幅值和频率的规律性进行研究，选择合理的抑制电磁振动噪声的方法，有效抑制永磁同步电动机的电磁振动噪声。

2 力波次数和频率分析

本文所研究内容需做以下说明：

(1)电机为三相p对极60°相带永磁同步电机；

(2)把波长等于电枢周长2pτ(τ为极距)的2极波作为基准波，而传统分析电机的基波为p次波，本文仍称之为基波，其他各次谐波的次数相应增加p倍；

(3)规定转子基波旋转方向为正方向。

根据麦克斯韦应力张量法，电机中气隙磁场相互作用产生的单位面积径向电磁力的瞬时值可以表示如下[12]：

(1)

式中,b(θ,t)为电机气隙磁密；μ0为真空磁导率。

电机在负载情况下，气隙磁密为转子磁场与电枢反应磁场共同作用产生。负载情况下电机的电磁力波包含以下三部分内容：

(1)转子磁场自身(包括永磁体磁势与气隙磁导恒定分量作用产生的谐波磁场和永磁体磁势与气隙磁导谐波分量作用产生的转子齿谐波磁场)作用产生的电磁力，磁密次数记为μ，力波次数为γ=2μi或γ=μi±μj，其中μi和μj分别代表转子磁密第i次和第j次谐波；

(2)电枢反应磁场谐波自身作用产生的电磁力，磁场谐波次数记为ν，产生的力波次数为γ=2νi或γ=νi+νj；

(3)转子磁场与电枢反应磁场谐波相互作用产生的电磁力，力波次数记为γ=μi±νj。

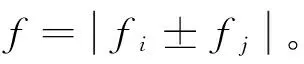
2.1 力波次数分析

令每极每相槽数：

(2)

式中，Z1为定子槽数；Ns为每槽导体数；Ns/d为最简分数[13,14]。

(1)d为偶数

当d为偶数时，单元电机数t=2p/d，则d=2p/t，Z1=(Ns/d)(6p)=3Nst，永磁体磁势与气隙磁导恒定分量作用产生的谐波磁场次数记为μ1，可以由式(3)确定：

(3)

式中，k2=0，1，2，…。

永磁体磁势与气隙磁导谐波分量作用产生的转子齿谐波次数记为μ2，可以由式(4)确定：

(4)

式中，l1=1，2，…。

电枢反应磁场谐波次数记为ν，可以表示如下：

当k1中存在某个数k1i，使得(3ki+1)t=p时，

ν=(3k1+1)t

(5)

当k1中存在某个数k1i，使得(3ki+1)t=-p时，

ν=-(3k1+1)t

(6)

式中，k1=0，±1，±2，…。

可知，当d为偶数时，转子磁场谐波次数μ1和μ2都为t的整数倍，电枢反应磁场谐波次数ν也均为t的整数倍。这样，磁场中任意两个谐波相互作用产生的电磁力次数必为t的整数倍。

(2)d为奇数

当d为奇数时，单元电机数t=p/d，则d=p/t，Z1=(Ns/d)(6p)=6Nst，永磁体磁势与气隙磁导恒定分量作用产生的谐波磁场次数为：

μ1=(2k2+1)p=(2k2+1)dt

(7)

式中，(2k2+1)d必为奇数。

永磁体磁势与气隙磁导谐波分量作用产生的转子齿谐波次数为：

(8)

式中，[±6l1Ns+(2k2+1)d]必为奇数。

电枢反应磁场谐波次数可以表示如下：

当k1中存在某个数k1i，使得(6k1i+1)t=p时，

ν=(6k1+1)t

(9)

当k1中存在某个数k1i，使得(6k1i+1)t=-p时，

ν=-(6k1+1)t

(10)

式中，k1=0，±1，±2，…。

可知，当d为奇数时，转子磁场谐波次数μ1和μ2都为t的奇数倍，电枢反应磁场谐波次数ν也均为t的奇数倍。这样，磁场中任意两个谐波相互作用产生的电磁力次数必为t的偶数倍，即2t的整数倍。

2.2 力波频率分析

(1)转子磁场

永磁体磁势与气隙磁导恒定分量作用产生的谐波磁场μ1自身作用产生的电磁力波频率为：

(11)

式中，f0为电机基波频率。

当只考虑一阶齿磁导时，永磁体磁势与气隙磁导谐波分量作用产生的转子齿谐波磁场次数为：μ2=±Z1+μ1，而μ1=m1p，Z1=xp+h，其中，m1=1，3，5，…,x为任意正整数，h为小于p的正整数。

齿谐波μ2自身作用产生的力波次数为：

γ=(±Z1+μ1i)±(±Z1+μ1j)

(12)

齿谐波μ2自身作用产生的力波分两种情况，第一种情况力波的次数为μ1i±μ1j，频率为(γ/p)f0。

令y=±2x+m1i±m1j，则m1i±m1j=y∓2x，第二种情况力波对应频率为：

(13)

式中，x、y为常数。

可以看出，由μ2自身作用产生的力波，同一次数的力波最多只有两个频率。一般来说，当力波次数较小时，y比较小，对应力波频率也低。

μ1和μ2相互作用产生的力波次数为：

γ=(±Z1+μ1i)±μ1j=[(±x+m1i)±m1j]p+h=sp+h

(14)

式中，s=(±x+m1i)±m1j。

对应频率为：

(15)

式中，x、s为常数。

可以看出，由μ1与μ2作用产生的力波，同一次数的力波最多只有两个频率。一般来说，当力波次数较小时，y比较小，对应力波频率也低。

以20极24槽电机为例，考虑转子侧磁场作用产生的4次力波时，对应x=2，h=4，μ1和μ2自身作用都不会产生4次力波，只有两者相互作用能够产生4次力波，对应s=0，这些4次力波频率全部为2f0。

(2)电枢反应磁场

当忽略定子齿谐波时，电枢反应磁场作用产生的力波频率为2f0。

(3)转子磁场与电枢反应磁场相互作用

转子永磁体磁场与电枢反应磁场相互作用时，产生的力波频率为(μ/p±1)f0；转子齿谐波磁场与电枢反应磁场相互作用时，产生的力波频率为(mj±1)f0。

可以看出，转子侧磁场和电枢磁场相互作用产生的力波，对应同一次数可以有很多频率。所以，频率高的低次力波最有可能出现在转子磁场与电枢反应磁场相互作用的情况，特别是转子齿谐波与电枢反应磁场谐波相互作用时的情况。

3 力波幅值分析

电磁力波的三要素包括力波次数、力波频率和力波幅值。一般来说，对电磁振动噪声影响较大的是低次力波。低次力波中，针对幅值较大的力波，需要从削弱力波幅值和使力波频率远离固有频率两个角度考虑降低其对振动噪声的影响；而对于幅值较小的力波，只需考虑使其频率远离电机的固有频率即可。

本节以两台电机为例，使用有限元软件计算其气隙磁密，其中电枢反应磁场磁密采用负载磁密减去空载磁密进行等效；通过傅里叶分析得出对应的谐波次数；将有限元计算得到的谐波次数与第2节解析式中的谐波次数进行对比，结果基本一致。

然后本文对这两台电机的低次力波幅值进行研究，分析出能够产生较大幅值力波的磁场谐波类型。

3.1 8极48槽电机

8极48槽电机的d=1，t=p=4。该电机磁力线分布如图1所示。由永磁体磁势产生的空载气隙磁密谐波次数如图2(a)所示，谐波次数符合(2k2+1)p，该电机齿谐波含量非常少，可以忽略。电枢反应磁场谐波次数如图2(b)所示，谐波次数与(6k1+1)p基本一致。

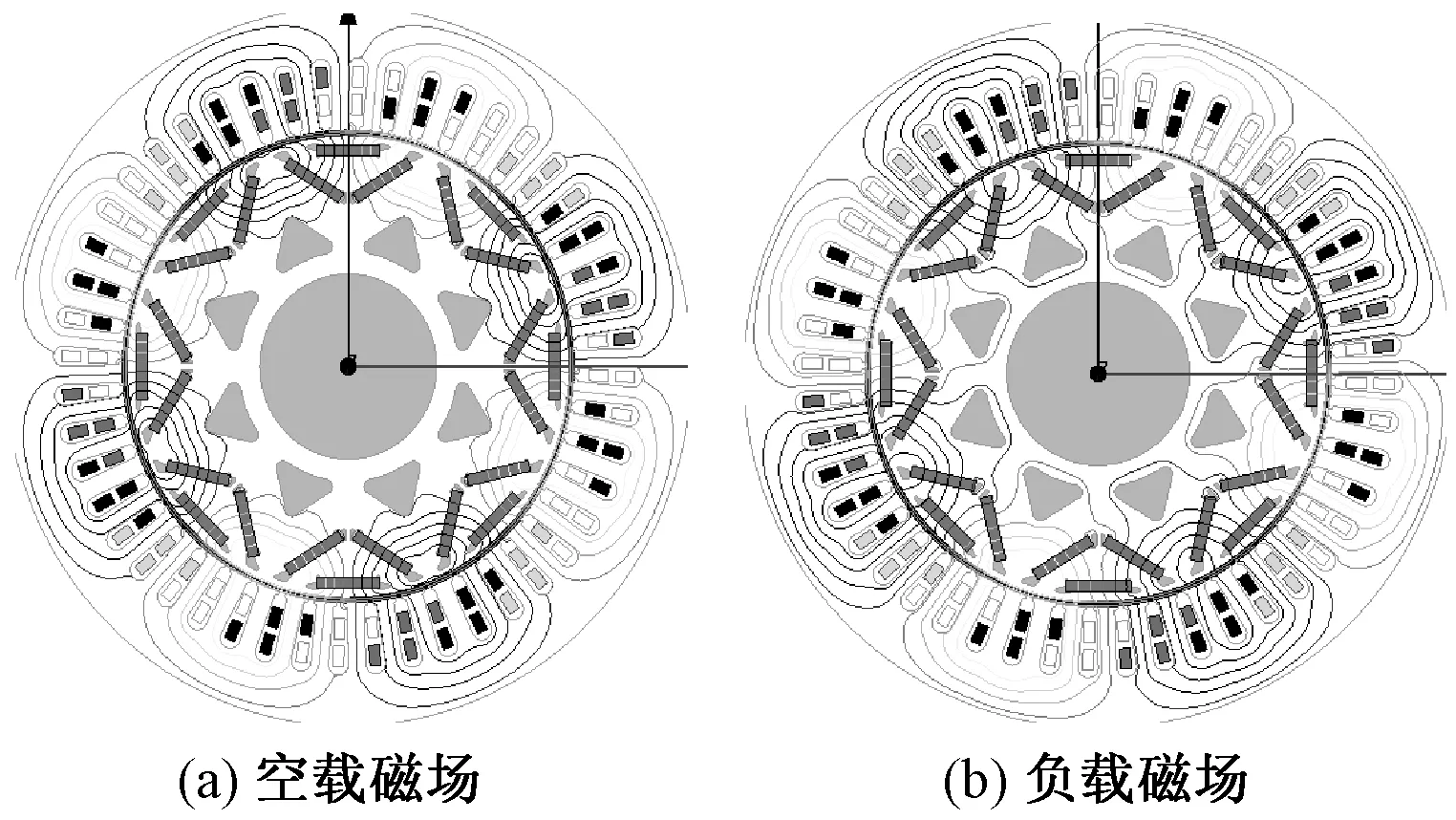
图1 8极48槽电机磁力线分布Fig.1 Field distributions for motor with 8 poles and 48 slots

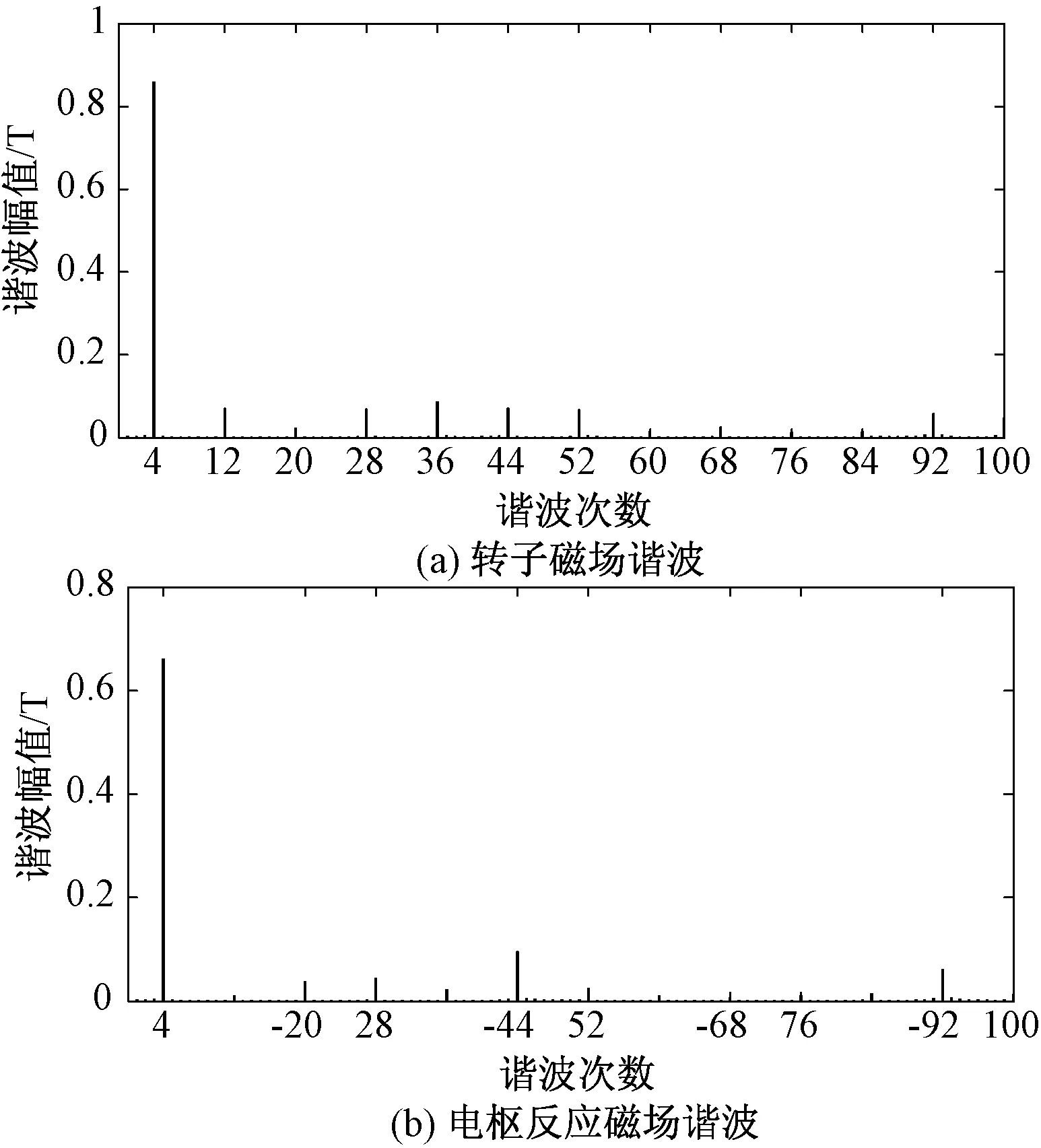
图2 8极48槽电机气隙磁场谐波Fig.2 Harmonics in air gap field for motor with 8 poles and 48 slots

转子磁场与电枢反应磁场相互作用时，能够产生0次力波，如图3(a)所示；转子磁场自身作用产生的最低次力波为8次力波，幅值如图3(b)所示；电枢反应磁场自身作用产生的最低次力波为8次力波，幅值如图3(c)所示；转子磁场与电枢反应磁场相互作用产生的次数最小的非0力波为8次力波，如图3(d)所示。

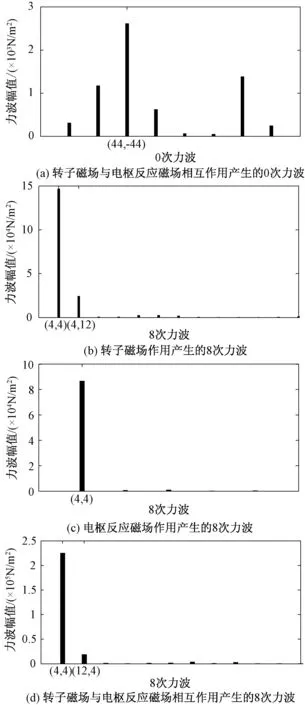
图3 8极48槽电机径向力波Fig.3 Harmonics in radial magnetic force for motor with 8 poles and 48 slots

从图3可以看出，8极48槽电机0次力波中，(44，-44)对应的0次力波幅值略大，总体来说，0次力波幅值均比较小。该电机所有8次力波中，转子磁场基波与电枢反应磁场基波自身作用或两者相互作用产生的8次力波幅值远大于其他8次力波幅值；基波附近转子12次谐波与两基波作用产生的力波幅值也较大；而其他磁场谐波产生的8次力波幅值都很小，在削弱这些小幅值力波引起的电磁振动噪声时仅考虑使其频率远离固有频率即可。

3.2 20极24槽电机

以20极24槽电机为例，d=5，t=2。该电机磁力线分布如图4所示。其转子磁场谐波次数如图5(a)所示，可以看出，该电机所包含的谐波次数可以认为是6、10、-14、26、30、34、46、50、54、66、70、74、90、94。其中10的倍数次波为永磁体磁势与气隙磁导恒定分量作用产生的谐波，对应次数为μ1=(2k2+1)p；其余的为转子齿谐波，对应次数为μ2=±Z1+μ1。电枢反应磁场谐波次数如图5(b)所示，与(6k1+1)t基本一致，其他次数的谐波幅值均很小，可以忽略。

图4 20极24槽电机磁力线分布Fig.4 Field distributions for motor with 20 poles and 24 slots

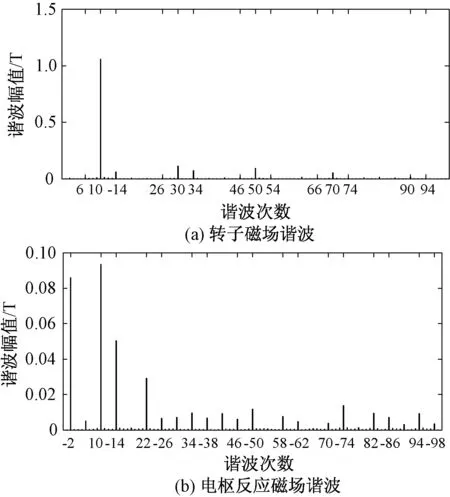
图5 20极24槽电机气隙磁场谐波Fig.5 Harmonics in air gap field for motor with 20 poles and 24 slots

20极24槽电机转子磁场与电枢反应磁场相互作用产生的0次力波如图6(a)所示；转子磁场自身作用产生的次数最低的力波为4次力波，如图6(b)所示；电枢反应磁场自身作用产生的最低次力波为4次力波，如图6(c)所示；转子磁场与电枢反应磁场作用产生的4次力波如图6(d)所示。

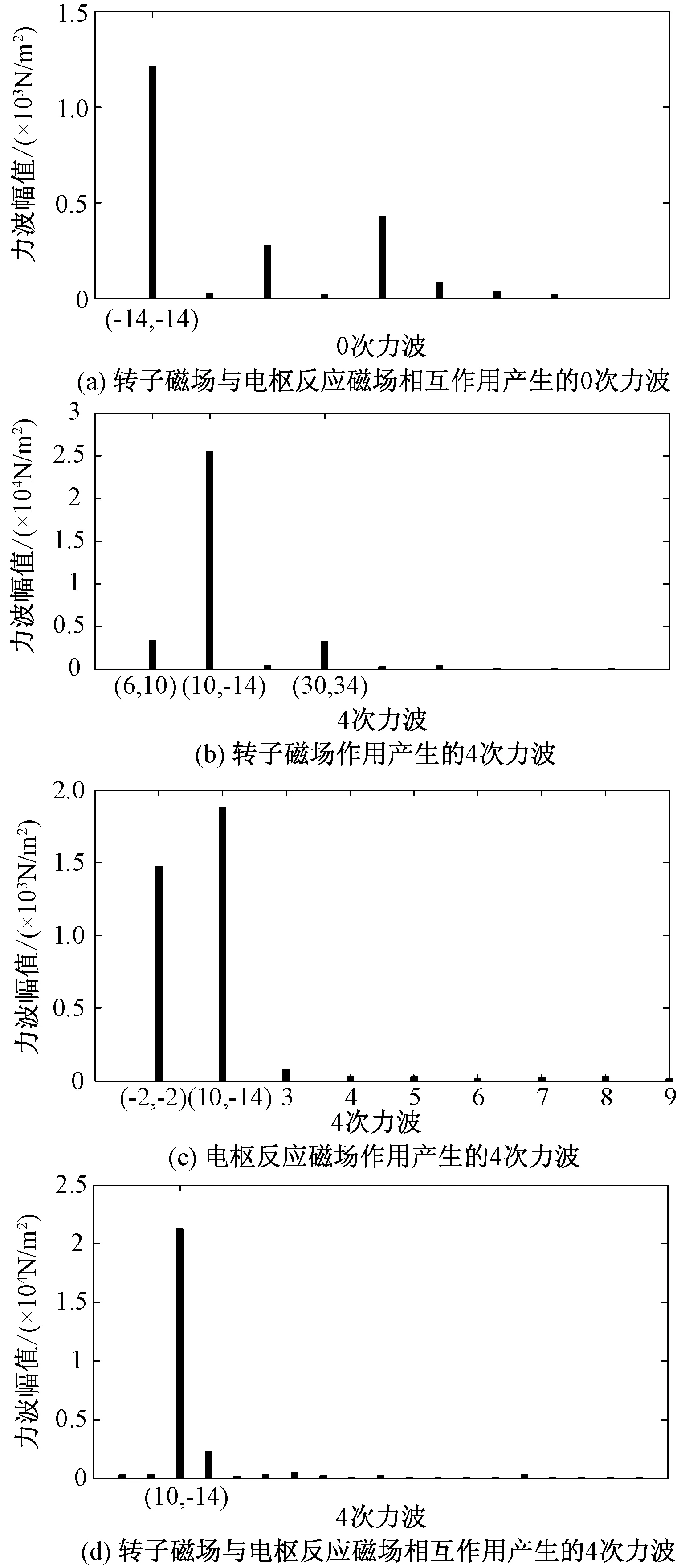
图6 20极24槽电机径向力波Fig.6 Harmonics in radial magnetic force for motor with 20 poles and 24 slots

从图6可以看出，0次力波幅值均很小。该电机所有4次力波中，与基波相关的4次力波幅值远大于其他4次力波幅值；与低于基波次数的次谐波相关的或转子磁场3p次谐波相关的4次力波幅值也较大；其他4次力波幅值均很小。

4 结论

(1)0次力波一般由两磁场的高次谐波相互作用产生，频率范围较广，幅值较小。

(2)当d为偶数时，非0力波次数为t的整数倍；当d为奇数时，非0力波次数为2t的整数倍；提高单元电机数可有效提高非0力波次数。

(3)由t≥1可知，只有d为偶数的分数槽电机可能出现单边磁拉力。

(4)永磁体磁势与气隙磁导恒定分量作用产生的谐波磁场μ1自身作用产生的电磁力波频率为f=(γ/p)f0；齿谐波μ2自身作用产生的力波频率为|y∓2x|f0；μ1和μ2相互作用产生的力波频率为|s∓x|f0；转子磁场μ和电枢反应磁场ν相互作用产生的力波频率为(μ/p±1)f0或(mj±1)f0；高频低次力波最有可能发生在两磁场相互作用时。

(5)与p次基波、转子3p次谐波、次谐波有关的低次力波幅值较大，其他低次力波幅值很小。

[1] 唐任远(Tang Renyuan). 现代永磁电机(Modern permanent magnet machines) [M]. 北京: 机械工业出版社 (Beijing: China Machine Press), 1997.

[2] Z Q Zhu, Z P Xia, L J Wu, et al. Analytical modeling and finite element computation of radial vibration force in fractional-slot permanent magnet brushless machines [A]. IEMDC [C]. 2009. 157-164.

[3] Z Q Zhu, Z P Xia, L J Wu, et al. Influence of slot and pole number combination on radial force and vibration modes in fractional slot PM brushless machines having single- and double-layer windings [A]. ECCE [C]. 2009. 3443-3450.

[4] G Dajaku, D Gerling. Magnetic radial force density of the PM machine with 12-teeth/10-poles winding topology [A]. IEMDC [C]. 2009. 2078-2083.

[5] 张冉, 王秀和, 杨玉波,等 (Zhang Ran, Wang Xiuhe, Yang Yubo, et al.). 基于等效剩磁法的永磁电动机转子偏心磁场解析计算(Analytical prediction of magnetic field in permanent magnet motors with rotor eccentricity based on the method of equivalent remanence) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2009, 24(5): 7-12.

(，cont.onp.22)(，cont.fromp.5)

[6] 张冉, 王秀和, 乔东伟, 等 (Zhang Ran, Wang Xiuhe, Qiao Dongwei, et al.). 磁极偏心削弱永磁电机激振力波方法 (Reduction of exciting force wave for permanent magnet motors by eccentric magnet pole) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2010, 30(27): 20-25.

[7] 张冉, 王秀和, 乔东伟, 等 (Zhang Ran, Wang Xiuhe, Qiao Dongwei, et al.). 基于辅助槽的永磁电机激振力波削弱方法 (Reduction of exciting force wave for permanent magnet motors by teeth notching) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2010, 30(18): 103-108.

[8] 张冉, 王秀和, 乔东伟 (Zhang Ran, Wang Xiuhe, Qiao Dongwei). 极弧系数选择对永磁无刷直流电机激振力波的影响 (Influence of pole-arc coefficient on exciting force waves of permanent magnet brushless DC motors) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2010, 30(21): 79-85.

[9] H C M Mai, R Bernard, P Bigot, et al. Consideration of radial magnetic forces in brushless DC motors [A]. ICEMS [C]. 2010. 1-6.

[10] 宋志环 (Song Zhihuan). 永磁同步电动机电磁振动噪声源识别技术的研究(Research on recognition of electromagnetic noise and vibration of permanent magnet synchronous machine) [D]. 沈阳: 沈阳工业大学 (Shenyang: Shenyang University of Technology), 2010.

[11] 杨浩东, 陈阳生, 邓志奇(Yang Haodong，Chen Yangsheng，Deng Zhiqi). 永磁同步电机常用齿槽配合的电磁振动(Electromagnetic vibration of PM synchronous motors with different combinations of slot and pole number) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2011, 26(9): 24-30.

[12] 陈世坤 (Chen Shikun). 电机设计 (Design of electrical motor) [M]. 北京: 机械工业出版社 (Beijing: China Machine Press), 2004.

[13] 许实章 (Xu Shizhang). 交流电机绕组理论 (AC machine winding theory) [M]. 北京: 机械工业出版社 (Beijing: China Machine Press), 1985.

[14] 陈世元, 黄士鹏 (Chen Shiyuan，Huang Shipeng). 交流电机的绕组理论 (Windings theory of A. C. machines) [M]. 北京: 中国电力出版社 (Beijing: China Electril Power Press), 2007.

Research on radial magnetic forces of permanent magnet synchronous motor supplied by sine wave

HAN Xue-yan， LI Sheng-xiang， MI Xiu-feng

(National Engineering Research Center for REPM Electrical Machines of Shenyang University of Technology， Shenyang 110870， China)

The radial magnetic force (RMF) is the main source of noise and vibration in permanent magnet synchronous motors (PMSMs). The methods to suppress it can be summarized as: (1) to increase the orders of radial force, (2) to reduce the amplitude of the radial force and (3) to make the frequency of the force away from the natural frequency. This paper analyzes the orders and frequencies of the radial force of PMSMs and summarizes the correlation between the radial force orders and the corresponding vibration frequencies. Based on the finite element analysis of the air gap magnetic harmonic fields of two motors, the amplitude of low order radial force generated by the air gap field is calculated to find out the harmonics which can cause radial forces with low orders and large amplitude.

vibration and noise; electromagnetic force waves; permanent magnet synchronous motor (PMSM); unbalanced magnetic force

2015-06-03

国家科技支撑计划资助项目(2015BAF06B00)

韩雪岩(1978-)， 女， 黑龙江籍， 副教授， 博士， 研究方向为特种电机及其控制; 李生祥(1990-)， 男， 辽宁籍， 硕士研究生， 研究方向为新型起重机用永磁电机设计。

TM351

A

1003-3076(2016)04-0001-05