计及风速与负荷相关性的配电网重构方法
2016-05-22李春燕罗洪飞
李春燕,杨 强,魏 蔚,罗洪飞,张 谦
(重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
0 引言
配电网通常具有闭环设计、开环运行的特点,其上配置了较多分段开关和联络开关等,通过改变这些开关的开、合状态可以改变配电网结构。因此,配电网重构就是在满足系统约束的条件下,通过改变开关的状态来改变网络拓扑结构,从而达到降低网络损耗、平衡负荷和提高供电可靠性等目的[1]。
近年来,风力发电作为分布式发电DG(Distributed Generation)的一种重要形式,技术发展迅猛,风电机组 WTG(Wind Turbine Generator)接入传统配电网是配电智能化的发展趋势。但WTG出力的随机性和间歇性,势必会对配电网系统产生较大影响[2]。
国内外已对含DG的配电网重构展开研究。文献[3]基于概率模型描述风电随机出力,根据风速与输出功率间的关系,将不同功率输出作为不同场景,通过选择不同场景建立计及风电出力随机影响的配电网重构场景模型。文献[4-6]提出在重构过程中将分布式电源的输出功率和负荷视为恒定,忽略了DG出力的随机性特点。这些文献均基于恒定负荷模型,且未计及风速与负荷相关性的影响。在含WTG的配电网中,风速和负荷受多种气候因素影响而随机变化,二者具有一定相关性,并非独立随机变量,且这种相关性对配电网潮流和重构的影响不能忽略。
国内外已有一些关于风速与负荷相关性的研究。文献[7]考虑与负荷相关的温度变化对风速的影响,对风速进行自回归滑动平均ARMA(Auto Regression Moving Average)预测,采用非参数估计的方法得到含温度参量的时序风速。文献[8]建立了时序风速-负荷模型,研究风电容量裕度时计及负荷变化的影响。文献[9]假设风速、负荷均服从正态分布,通过二者的线性相关系数,建立了基于二元正态分布的风速与负荷相关性模型,研究了风速与负荷相关性对配电网可靠性的影响。上述文献建立的模型精度较差,且鲜有文献研究风速与负荷相关性对配电网重构的影响。文献[10]应用Copula理论建立了风电场、光伏电站出力联合概率分布模型,没有分析风速与负荷间的相关性,但可以借鉴该文方法进行变量间相关性的研究。文献[11]将Copula理论与蒙特卡洛仿真法相结合,提出了一种处理输入随机变量相关性的概率潮流计算方法,但没有分析风速与负荷的相关性对配电网重构的影响。因此,如何在配电网重构中计及风速与负荷相关性的影响,用联合分布描述二者的相关性,建立更精确的数学模型具有重要研究意义。
综上,本文通过建立基于Copula理论的风速与负荷相关性模型,提出了一种计及二者相关性的配电网重构优化方法。
1 基于Copula理论的风速与负荷相关性模型
1.1 Copula理论
传统相关性模型在应用中存在一定不足:各随机变量边缘分布必须相同;只能解决一些特殊的多元分布;基于线性相关系数进行变换会改变原始样本的相关结构等[9,12-13]。 而 Copula 函数理论因其具有很多优良的特性,可以解决这一难题。Copula函数是一类将多元联合分布函数与变量各自的边缘分布连接在一起的函数,也称作连接函数,它描述了变量间的相关性[14]。
Sklar 定理[15]:令 F(x1,x2,…,xN)为具有边缘分布 F1(x1)、F2(x2)、…、FN(xN)的联合分布函数,那么存在一个 Copula函数 C(·,…,·),满足式(1):
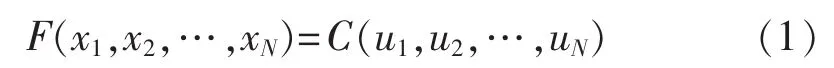
其中,u1=F1(x1),u2=F2(x2),…,uN=FN(xN)。 若边缘分布 F1(x1)、F2(x2)、…、FN(xN)连续,则 Copula 函数 C唯一确定。
Sklar定理是Copula理论的应用基础。Copula函数构造相关性模型的优点在于不必要求各变量具有相同的边缘分布,任意边缘分布经过Copula函数都可以构造成联合分布,而且几乎不会改变原始样本的相关结构,这与传统矩阵变换法和正态变换法构造相关性模型相比更为精确。
1.2 Copula函数的选取
常用的 Copula函数有正态 Copula函数、t-Copula函数以及阿基米德Copula函数等,由于阿基米德Copula函数具有构造简单、计算方便等特点,因此本文采用阿基米德Copula函数来构造风速与负荷的相关性模型。
N元阿基米德Copula函数的表达式如下[16]:

其中,φ(·)为阿基米德 Copula函数的生成元(generator),φ-1(·)为生成元的逆函数。
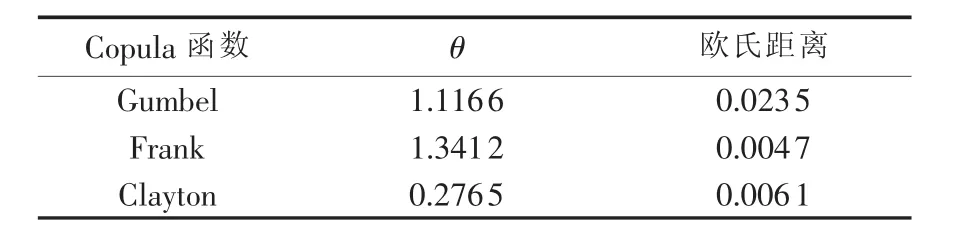
阿基米德Copula函数形式由其生成元决定,常用的阿基米德Copula函数及生成元见表1,表中θ为相应参数。θ可采用极大似然估计法[17]进行估计。

表1 阿基米德Copula函数生成元Table1 Generator for three Archimedean Copula functions
要从给定的Copula函数中选择出最优的一个,需要根据一定的准则进行最优选取,也即拟合优度评价。有多种方法可以选择最优Copula函数,应用较多的是采用基于经验Copula函数的最短距离法[14]。经验Copula函数可表示为:
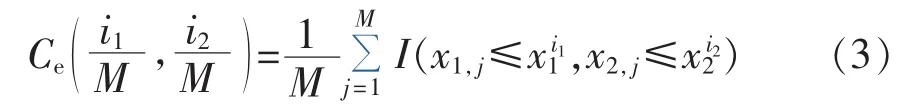
其中,I(·)为指示函数,若括号内条件满足,则I=1,反之 I=0;xki为顺序统计量且 1≤i1≤M、1≤i2≤M,M为样本容量。
经验与理论Copula函数之间的欧氏距离为:

依据上述公式的距离大小,选择具有最短距离的Copula函数作为最优Copula,用于描述风速与负荷随机变量间的相关结构。
1.3 风速与负荷的相关性建模
1.3.1 风速与负荷边缘分布
在以往的研究中,风速与负荷的边缘分布模型主要采用参数分布,如威布尔分布、瑞利分布和正态分布等[18]。但是,这些参数分布模型很难与实际样本分布精确拟合,因此本文采用经验分布[19]对样本数据进行概率变换,较之参数分布模型更加精确。
经验分布函数的表达式为:
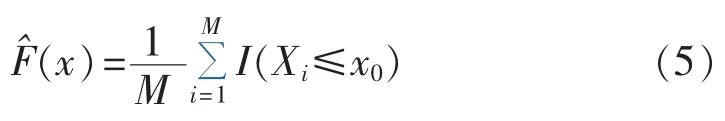
其中,M 为样本容量;Xi为样本点;I(Xi≤x0)表示样本中小于或者等于x0的样本点个数。
1.3.2 风力发电系统随机模型
风力发电机的输出有功功率随风速的变化而变化,其输出功率方程为:
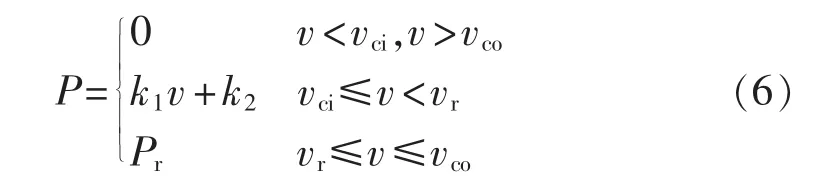
1.3.3 风速与负荷相关性模型的仿真
(1)基于Copula函数的样本产生。
对于N维相关随机变量,随机数的产生应该由多维随机变量的联合概率分布产生。基于Copula函数的样本产生算法有多种[14,20],本文采用一种基本的抽样方法,步骤如下。
a.产生N个服从(0,1)均匀分布的独立随机数,即 Z=(z1,z2,z3,…,zN)。
b.根据以下公式生成服从N维Copula函数的随机向量U=(u1,u2,u3,…,uN),即uk=C-1(u1,u2,…,uk-1)(zk)(k=1,2,…,N),其中:
其中,vci、vr和vco分别为风力发电机的切入风速、额定风速和切出风速;Pr为额定功率和k2=-k1vci为系数。
本文假设风力发电机能够按恒定功率因数运行,因此其无功出力为:

其中,δ为功率因数角,一般对于并网风力发电机而言功率因数角δ位于第四象限,即tan δ为负值,因此并网风力发电机吸收配电网的无功功率。
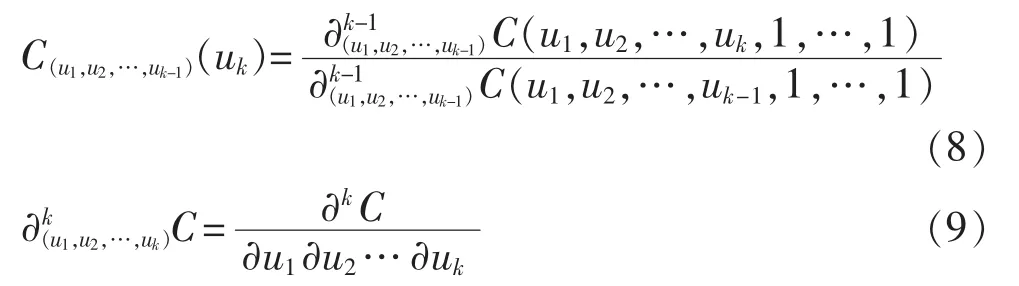
c.将生成的随机数向量U,根据各个随机变量各自的边缘分布Fk(xk)进行逆变换后,可得到满足式(1)的模拟样本数据。
(2)风速与负荷相关性模型的建立步骤如下:
a.由风速x1、负荷x2的历史统计数据,得到风速、负荷的边缘分布 F(x1)、F(x2),其中 ui=Fi(xi)(i=1,2)为各自对应的累积分布函数值;
b.选择合适的Copula函数,本文选取正态Copula以及3种阿基米德Copula函数作为风速与负荷相关性模型的备选函数;
c.利用极大似然估计法,估计各备选Copula函数中的参数θ;
d.计算各备选Copula函数经验与理论分布的欧氏距离,由最短距离法,从备选Copula中选择距离最小的Copula函数作为描述风速与负荷相关性的最优函数;
e.由Copula函数的抽样方法,对已经确定的最优Copula函数进行模拟抽样,生成一定规模的随机数向量 U=(u1,u2);
f.将生成的随机数向量U,根据风速与负荷各自的边缘分布Fk(xk)进行逆变换后,可得到计及相关性的风速与负荷的模拟样本数据。
2 计及风速与负荷相关性的配电网重构
2.1 配电网重构数学模型
配电网重构通常以降低网络损耗,提高供电可靠性、电压质量和平衡负荷等为目标,或是综合考虑上述多个指标为目标。本文以配电网的有功损耗期望值最小为目标函数,即:

其中,l为网络支路数;ki表示支路i开合状态,0表示打开,1表示闭合;ri为支路i电阻;Pi和Qi分别为流过支路i的有功和无功功率;Ui为支路i末端电压。
另外,配电网重构模型还需满足一定的约束条件,如潮流约束、辐射状运行约束、节点电压约束和支路容量约束等。
2.2 计及风速与负荷相关性的配电网随机潮流算法
风力发电机的输出功率主要由该时刻的风速决定,由于风速的不确定性,风力发电机的输出功率具有随机性,同时负荷大小在一定时间内也具有波动性。为研究风速、负荷随机性以及风速与负荷相关性对配电网潮流的影响,基于建立的风速与负荷相关性模型,在蒙特卡洛模拟[21]计算前随机潮流的基础上,提出了一种计及风速与负荷相关性的配电网随机潮流算法,具体算法步骤如下。
a.由最优的Copula函数,产生KN组具有相关性的模拟风速与负荷序列对,由风力发电出力随机模型得到风机有功和无功功率。
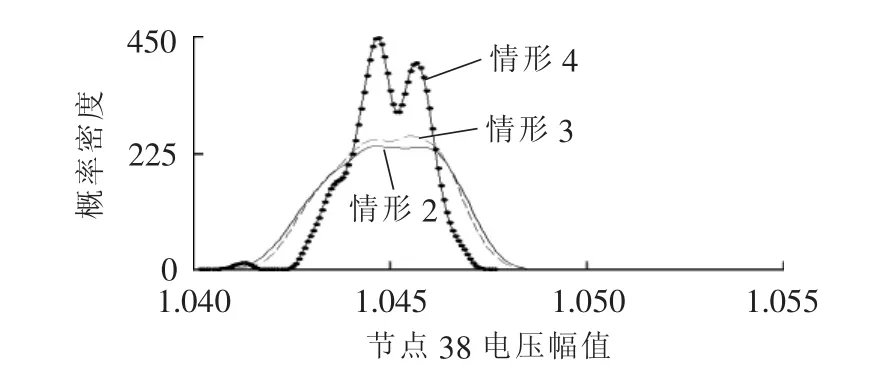
b.输入相关数据,根据蒙特卡洛模拟法计算K次确定性配电网潮流,K c.判断随机潮流计算结果的方差系数η是否满足蒙特卡洛模拟收敛条件。若满足,则停止增加潮流计算样本数,继续步骤d;若不满足,置K=K+1,返回步骤b。 d.由计及风速与负荷相关性的配电网潮流计算结果,得到有功损耗、节点电压等概率分布情况。 由于配电网具有闭环设计、开环运行的特点,传统的遗传算法在配电网重构的遗传操作过程中会产生大量非辐射状的不可行解。本文采用基于基本回路的遗传操作方案[22]对配电网进行重构。将配电网中的所有支路闭合,记为图G,并找出图G中的所有基本回路。配电网中的支路按图G中的基本回路按基因块编码,不在基本回路内的支路不用编码。这种编码方式既能缩短染色体长度,又可以在遗传操作中避免不可行解的产生。具体算法步骤如下: a.将配电网各基本回路按基因块编码,产生初始种群,使其满足各基因块内有且仅有一个0,即各基因块只有一条打开支路,置进化代数g=1; b.由计及风速与负荷相关性的蒙特卡洛配电网随机潮流算法,计算每个染色体所代表配电网的有功损耗期望值大小,并取其倒数为适应值函数,计算每个染色体的适应值; c.通过轮盘赌选择函数,对染色体进行选择操作; d.对染色体进行交叉操作,每次交叉操作只将对应基因块进行交换; e.对染色体进行变异操作,将某一基因块中为0的基因位取反变成1,同时将基因块中为1的某一基因位取反变成0; f.判断g是否达到最大进化代数gmax,若未达到,则置g=g+1,返回步骤b继续迭代,直到达到最大进化代数为止。 具体流程图如图1所示。 图1 计及风速与负荷相关性的配电网重构流程图Fig.1 Flowchart of DNR considering correlation between wind-speed and load 风速数据采用加拿大萨斯喀彻温地区一年统计风速[23],负荷数据采用IEEE-RTS系统时序负荷曲线,分别如图2和图3所示(图3中负荷为标幺值,后同)。设x、y分别表示风速与负荷样本,则其线性相关系数ρ计算公式如下: 其中,cov(x,y)为风速与负荷样本的协方差;D(x)与D(y)为其方差。 图2 加拿大萨斯喀彻温地区1997年时序风速曲线Fig.2 1997’s sequential wind-speed curve of Saskatchewan,Canada 图3 IEEE-RTS系统时序负荷曲线Fig.3 Sequential load curve of IEEE-RTS system 经计算风速与负荷样本的线性相关系数ρ=0.2007,说明样本风速与负荷存在弱的正相关性,为了定量刻画样本风速与负荷的相关变化情况,需要选择恰当的Copula函数,本文采用以上介绍的3种阿基米德Copula函数作为备选。 用极大似然估计法对3种阿基米德Copula函数进行参数估计,并采用最短距离法进行最优Copula函数的选取。理论分布和经验分布的欧氏距离见表2。由于Frank Copula的距离最小,因此Frank Copula是最优的Copula函数,本文选择Frank Copula来描述样本风速与负荷的相关结构。 表2 参数估计和欧氏距离Table 2 Parameter estimation and Euclidean distance 为定量和定性地评估采用Copula理论的风速与负荷相关性模型的准确性,分别采用Frank Copula函数理论与正态变换法[9]对该系统的风速和负荷进行数据模拟,模型对比结果如表3所示。可见,本文模型的相关系数为0.2006,其与原始样本的相关系数非常接近;风速、负荷均值和标准差比正态变换法更好,说明采用本文模型进行模拟采样后的数据分布特性与样本数据的分布特性保持一致。 表3 模型验证与对比Table 3 Model verification and comparison 图4和图5分别为Frank Copula函数方法和正态变换法的P-P图,可以看出Frank Copula函数所建立的风速-负荷相关性模型与样本风速-负荷具有相近的联合概率分布特性,拟合曲线更加接近直线。由上述结果说明,采用Copula理论进行风速与负荷的相关性建模具有很高的精度。 图4 Frank Copula函数理论的P-P图Fig.4 P-P plot of Frank Copula function theory 图5 正态变换理论的P-P图Fig.5 P-P plot of normal transformation 采用本文介绍的风速与负荷相关性模型,对美国PG&E69[22]配电网进行测试分析。 PG&E69节点配电网系统额定电压为12.66 kV,总的负荷大小为3802.19 kW+2694.60 kvar,共有73条支路,其中有5个联络开关。取平衡节点电压为1.05 p.u.,gmax=50,种群数为100,初始交叉率和变异率分别为0.9和0.1。假设在节点38和49处各并入额定功率为0.5 MW的风电机组,其切入风速、额定风速和切出风速分别为 3 m/s、13 m/s和 25 m/s,功率因数为 0.98。 表4所示为7种不同情形下的配电网结构和有功损耗期望值,其中,情形1为无风力发电,情形2为含风力发电、忽略风速-负荷相关性,情形3为含风力发电、风速-负荷部分相关(相关系数为0.2),情形4为含风力发电、风速-负荷完全相关(相关系数为1),情形5为含风力发电、忽略风速-负荷相关性的网络重构后,情形6为含风力发电、风速-负荷部分相关的网络重构后,情形7为含风力发电、风速-负荷完全相关的网络重构后。表5为重构前后的有功损耗期望值对比结果。首先,对比情形1知,风力发电接入配电网后会降低配电网的有功损耗,有效改善潮流分布,使系统能更经济地运行;其次,对比情形2—4知,随着风速与负荷相关性的增强,配电网的有功损耗期望值逐渐降低;情形3与情形2相比,有功损耗期望值降低了1.18 kW(1.11%);情形4与情形2相比,有功损耗期望值降低了5.60 kW(5.29%)。可见风速与负荷相关性的强弱对配电网有功损耗影响较大,特别是二者相关性较强时,对配电网随机潮流的影响不能忽略。图6为情形2—4的配电网有功损耗概率密度曲线,可见风速与负荷相关性的强弱对配电网有功损耗概率分布也有较大影响,当二者相关性增强时,概率分布波动范围变窄,更加密集。 表4 配电网结构和网络损耗Table 4 Distribution network structure and power loss 表5 重构前后有功损耗期望值对比Table 5 Comparison between expectation of active power loss before reconfiguration and that after reconfiguration 图6 情形2—4配电网有功损耗概率密度曲线Fig.6 Probability density curve of active power loss of distribution network in case 2-4 对比重构前的情形2—4与重构后的情形5—7,结果表明配电网重构后其有功损耗期望值较重构前初始网络有了明显的降低;由情形5—7可知,风速与负荷的相关性强弱不仅对配电网有功损耗期望值大小有影响,而且当二者相关性较强时也会使配电网重构方案发生一定变化,情形5、6的联络开关集合为{10-65,12-19,13-14,44-45,49-50},而当风速与负荷完全相关的情形7的联络开关集合为{10-65,12-19,11-12,44-45,49-50}。 因此,在对含风力发电的配电网进行配电网重构时,不能忽略风速-负荷相关性所带来的结果影响。 图7、8为风力发电机接入节点38的电压(幅值和相角)概率密度曲线(图中电压幅值和相角均为标幺值),表6为其电压均值和标准差(均为标幺值)。可见,风速与负荷相关性的强弱也会对配电网电压概率分布产生较大影响。情形3与情形2相比,节点38电压幅值与相角的均值相同而电压幅值与相角的标准差分别相差了7.14%与9.52%;情形4与情形2相比,节点38电压幅值与相角的均值分别相差了0.01%与33.33%,而其电压幅值与相角的标准差分别相差了35.71%与38.10%。因此,当风速与负荷相关性较强时,不能忽略对配电网随机潮流计算所带来的误差。 图7 情形2—4节点38电压幅值概率密度曲线Fig.7 Voltage amplitude probability density curve of node 38 in case 2-4 图8 情形2—4节点38电压相角概率密度曲线Fig.8 Voltage phase probability density curve of node 38 in case 2-4 Copula函数描述了随机变量间的相关结构,是构造多元相关随机变量联合分布的有力工具。本文通过建立基于Copula理论的风速与负荷相关性模型,并选择最优的Frank Copula来描述样本风速与负荷的相关结构,实验证明该函数能够较好地解决风速与负荷相关性问题。 采用基于基本回路的遗传操作方案对算例配电网进行重构优化,结果表明风速与负荷相关性强弱对配电网随机潮流和重构方案都有一定的影响。忽略二者相关性的影响,会对配电网随机潮流计算和重构优化方案带来一定误差,从而降低对配电网优化运行与规划的参考价值。 [1]孙惠娟,彭春华,袁义生.综合开关次数分析的配电网多目标动态重构[J].电力自动化设备,2014,34(9):41-46.SUN Huijuan,PENG Chunhua,YUAN Yisheng.Multi-objective dynamic distribution network reconfiguration considering switching frequency[J].Electric Power Automation Equipment,2014,34(9):41-46. [2]梁有伟,胡志坚,陈允平.分布式发电及其在电力系统中的应用研究综述[J].电网技术,2003,27(12):71-75.LIANG Youwei,HU Zhijian,CHEN Yunping.A survey of distributed generation and its application in power system[J].Power System Technology,2003,27(12):71-75. [3]何禹清,彭建春,文明,等.含风电的配电网重构场景模型及算法[J].中国电机工程学报,2010,30(28):12-18.HE Yuqing,PENG Jianchun,WEN Ming,et al.Scenario model and algorithm for the reconfiguration of distribution network with wind power generators[J].Proceedings of the CSEE,2010,30(28):12-18. [4]崔金兰,刘天琪,李兴源.含有分布式发电的配电网重构研究[J].电力系统保护与控制,2008,36(15):37-40.CUI Jinlan,LIU Tianqi,LI Xingyuan.Network reconfiguration at the distribution system with distributed generation[J].Power System Protection and Control,2008,36(15):37-40. [5]RAYAPUDI S R,SADHU V L N,MANYALA R R,et al.Optimal network reconfiguration of large-scale distribution system using harmony search algorithm[J].IEEE Transactions on Power Delivery,2011,26(3):1080-1088. [6]麻秀范,崔换君.改进遗传算法在含分布式电源的配电网规划中的应用[J].电工技术学报,2011,26(3):175-180.MA Xiufan,CUI Huanjun.An improved genetic algorithm for distribution network planning with distributed generation[J].Transactions of China Electrotechnical Society,2011,26(3):175-180. [7]CALLAWAY D S.Sequential reliability forecasting for wind energy:temperature dependence and probability distributions[J].IEEE Transactions on Energy Conversion,2010,25(2):577-585. [8]JAYAWEERA D,ISLAM S.Probabilistic assessment of distribution network capacity for wind power generation integration [C]//Power Engineering Conference.Adelaide,SA,USA:IEEE,2009:1-6. [9]孙若迪,谢开贵.计及风速-负荷相关性的配电网可靠性评估Monte Carlo 模拟法[J].电力系统保护与控制,2012,40(18):12-18.SUN Ruodi,XIE Kaigui.Reliability evaluation of distribution networksusing Monte Carlo method considering correlations between wind speed and load[J].Power System Protection and Control,2012,40(18):12-18. [10]赵继超,袁越,傅质馨,等.基于Copula理论的风光互补发电系统可靠性评估[J].电力自动化设备,2013,33(1):124-129.ZHAO Jichao,YUAN Yue,FU Zhixin,et al.Reliability assessment of wind-PV hybrid generation system based on Copula theory[J].Electric Power Automation Equipment,2013,33(1):124-129. [11]蔡德福,石东源,陈金富.基于Copula理论的计及输入随机变量相关性的概率潮流计算[J].电力系统保护与控制,2013,41(20):13-19.CAI Defu,SHI Dongyuan,CHEN Jinfu.Probabilistic load flow considering correlation between input random variables based on Copula theory correlation between Copula theory[J].Power System Protection and Control,2013,41(20):13-19. [12]张里,刘俊勇,刘友波,等.计及风速相关性的电网静态安全风险评估[J].电力自动化设备,2015,35(4):84-89.ZHANG Li,LIU Junyong,LIU Youbo,et al.Static security risk assessment of power system considering wind speed correlation[J].Electric Power Automation Equipment,2015,35(4):84-89. [13]QIN Zhilong,LI Wenyuan,XIONG Xiaofu.Generation system reliability evaluation incorporating correlation of wind speeds with different distributions[J].IEEE Transactions on Power Systems,2013,28(1):551-558. [14]NELSEN R B.An introduction to Copulas[M].New York,USA:Springer,2006:17-42. [15]TRIVEDI P K,ZIMMER D M.Copula modeling:an introduction for practitioners[M].Boston,USA:Now Publishers Inc,2007:9-12. [16]GENEST C,MACKAY J.The joy of Copulas:bivariate distributions with uniform marginals[J].The American Statistician,1986,40(4):280-283. [17]CHERUBINI U,LUCIANO E,VECCHIATO W.Copula methods in finance[M].Cornwall,England:John Wiley&Sons,2004:153-158. [18]CARTA J A,RAMIREZ P,VELÁZQUEZ S.A review of wind speeds probability distributions used in wind energy analysis:case studies in the Canary Islands[J].Renewable and Sustainable Energy Reviews,2009,13(5):933-955. [19]TURNBULL B W.The empirical distribution function with arbitrarily grouped,censored and truncated data[J].Journal of the Royal Statistical Society:Series B(Methodological),1976,38(3):290-295. [20]韦艳华,张世英.Copula理论及其在金融分析上的应用[M].北京:清华大学出版社,2008:1-5. [21]LI Wenyuan.Risk assessment of power systems:models,methods and applications[M].New York,USA:IEEE Press and John Wiley&Sons Inc,2005:79-87. [22]杨建军,战红.基于图论的改进遗传算法在配网重构中的应用[J].电力系统保护与控制,2010,38(21):122-125.YANG Jianjun,ZHAN Hong.Application ofthe improved genetic algorithm based on graph theory in distribution network reconfiguration[J].Power System Protection and Control,2010,38(21):122-125. [23]Climate.Historical climate data of Canada[EB/OL].[2015-03-02].http://climate.weather.gc.ca/.2.3 计及风速与负荷相关性的配电网重构算法

3 算例分析
3.1 风速与负荷相关性模拟

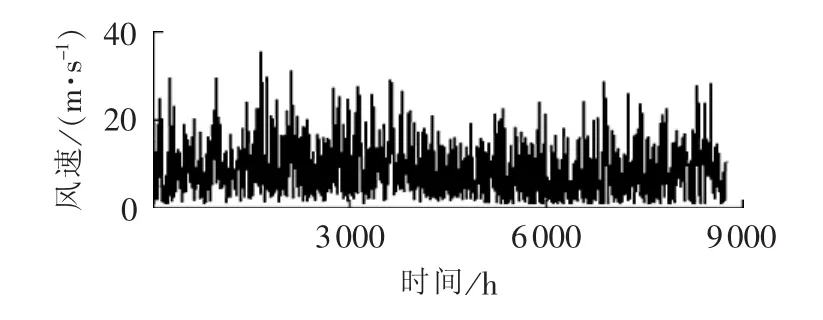
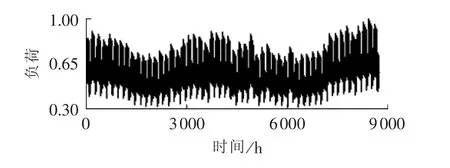
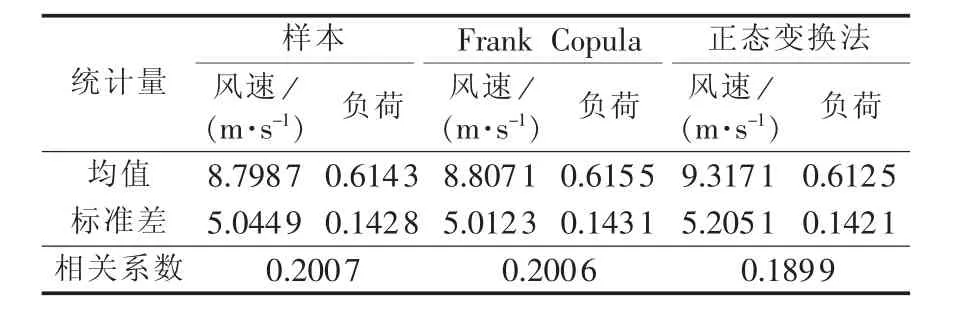
3.2 模拟的验证与对比


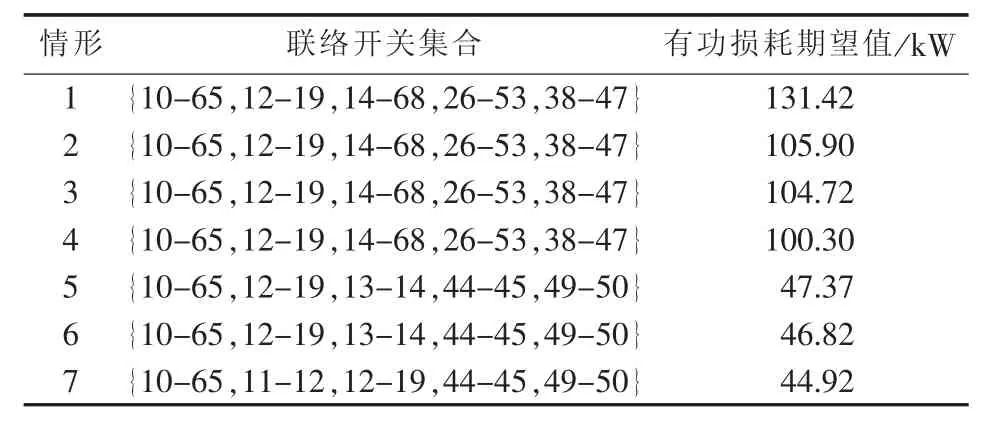
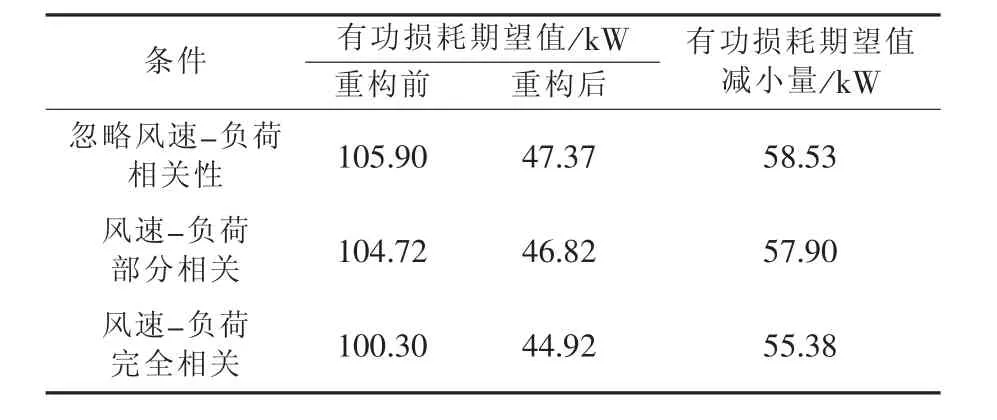
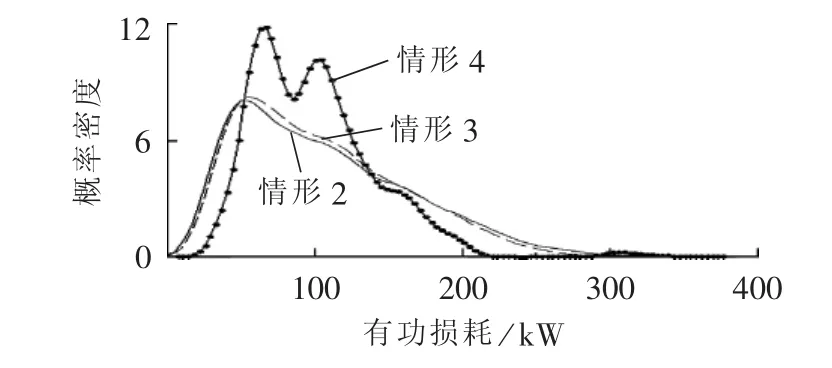
3.3 计及相关性的配电网随机潮流和重构结果

4 结论
