炭黑增强BR硫化胶的压缩Mullins效应的“放大器效应”研究*
2016-05-21张纪凯王兆波
张纪凯,刘 通,王兆波
(青岛科技大学 材料科学与工程学院,山东 青岛 266042)
顺丁橡胶(BR)是目前仅次于丁苯橡胶(SBR)的第二大通用合成橡胶[1]。BR因具有弹性和耐屈挠性能好、耐磨性优异、生热低、滞后损失小以及原料资源丰富、价格低等特点,被广泛用于轮胎和胶带、胶管等橡胶制品的生产[2]。
Mullins效应是橡胶首次变形后发生的软化现象,它伴随着残留变形和诱导产生的各向异性[3]。尽管人们对Mullins效应的研究已有数十年的历史,并建立了断键、分子滑移[4]、填料网络破坏和解缠绕[5]等模型,试图解释其形成机理[6],但Mullins效应仍被公认为是橡胶类材料力学行为研究的难点。
本研究以炭黑(CB)增强BR硫化胶为研究对象,对其力学性能以及压缩模式下的Mullins效应的“放大器效应”进行了系统研究。
1 实验部分
1.1 原料
BR:9000型,顺式1,4结构质量分数为96%,中国石油新疆独山子石化公司;CB:N220,天津市金秋实化工有限公司;硫黄、促进剂TMTD、促进剂CZ、ZnO、硬脂酸及防老剂4010等均为工业级配合剂。
1.2 仪器设备
X(S) K-160型双辊开炼机和50 T平板硫化机:上海群翼橡塑机械有限公司;GT-TCS-2000型伺服控制拉力试验机:台湾高铁科技股份有限公司;CH-10型厚度计:扬州市俊平试验机械有限公司;LX-A型硬度仪:上海险峰电影机械厂。
1.3 试样制备
BR硫化胶配方(质量份)为:BR 100,氧化锌 5,硬脂酸 2,防老剂D 1.5,防老剂4010 0.5,促进剂CZ 1.2,促进剂TMTD 0.35,硫黄 1,CB变量。
在室温开炼机上按配方制备BR混炼胶,下片;在160 ℃平板硫化机上,排气3~5次,按正硫化时间(t90)进行硫化,之后裁片制样。
1.4 性能测试
1.4.1 力学性能
拉伸强度和撕裂强度分别按GB/T 528—2009和GB/T 529—2008进行测试,拉伸速度为500 mm/min;硬度按GB/T 531—2008进行测试。
1.4.2 压缩Mullins效应
试样为圆柱状,高约10 mm,直径约10 mm。采用伺服控制拉力试验机进行单轴循环压缩测试(压缩Mullins效应),应变速率为0.008 3 s-1,其中一个试样进行单轴压缩实验,另一个进行循环单轴压缩实验,根据程序设定依次增加压缩应变,压缩应变定义参照GB/T 7757—1993,其值分别为10%、20%、30%、40%及50%。
特定压缩应变下每个循环中的应力峰值为最大压缩应力;每个循环结束时应力为零所对应的残留应变为瞬时残留压缩变形。
2 结果与讨论
2.1 CB增强BR硫化胶的力学性能
图1为CB增强BR硫化胶的应力-应变曲线。表1为CB增强BR硫化胶的力学性能。从图1可以看出,BR硫化胶均呈现出典型弹性体“软而韧”特征,随着CB用量的提高,初始模量略有提高,拉伸强度和断裂伸长率逐渐增加,且在CB用量为40 phr时断裂伸长率最大。
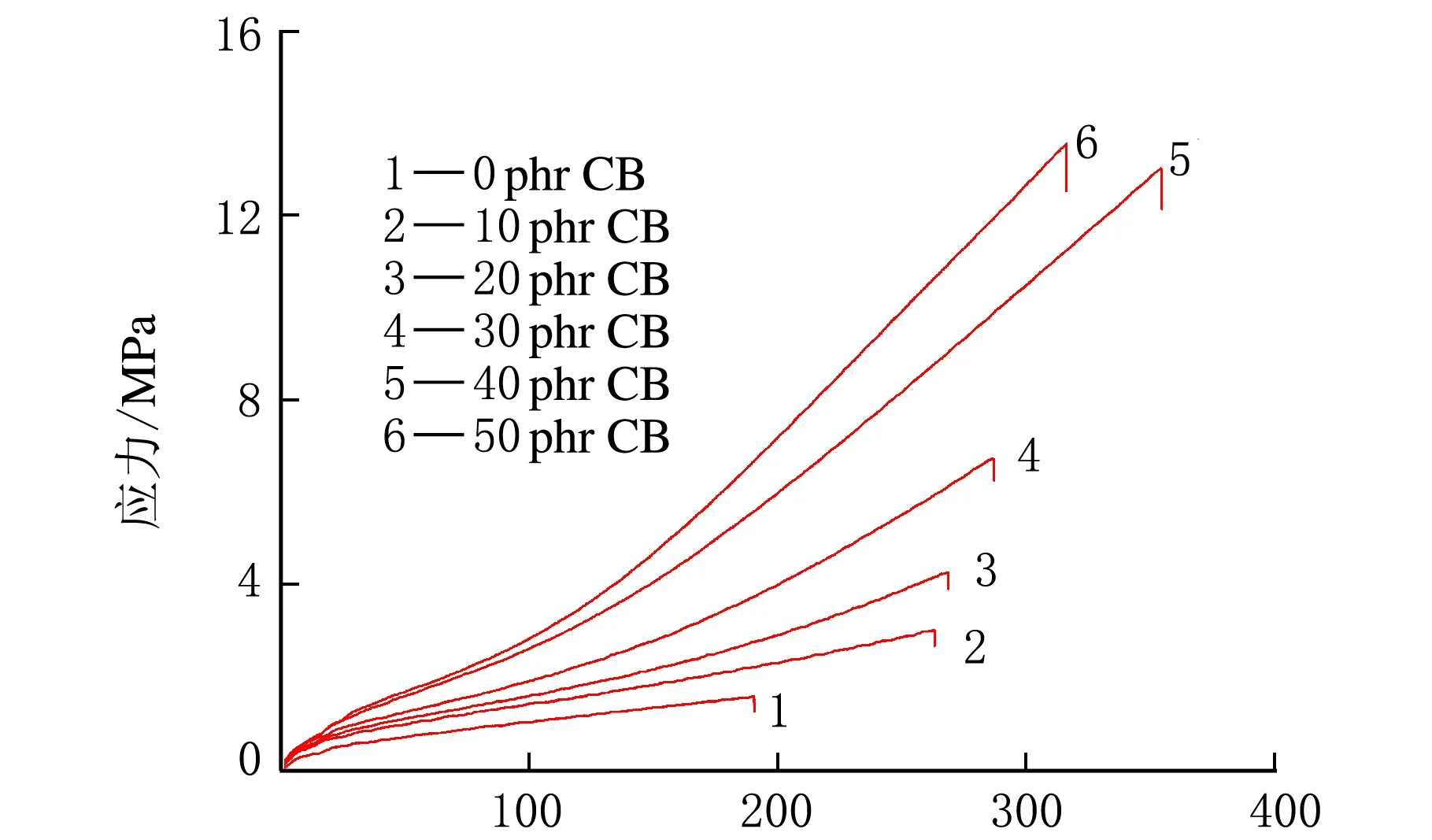
应变/%图1 CB增强BR硫化胶的应力-应变曲线

表1 CB增强BR硫化胶的力学性能
从表1可看出,未填充CB的BR硫化胶拉伸强度较弱,仅为1.4 MPa。填充CB后,其强度随CB用量的增加而呈现出大幅度的提升;永久变形和硬度均随CB用量的增加而增大。从表1还可看出,CB用量为40 phr时体系综合性能较好。
2.2 CB增强BR硫化胶的压缩Mullins效应
图2为不同用量CB增强BR硫化胶的单轴压缩及单轴循环压缩的应力-应变曲线。

压缩应变/%(a) 0 phr CB

压缩应变/%(b) 10 phr CB

压缩应变/%(c) 20 phr CB
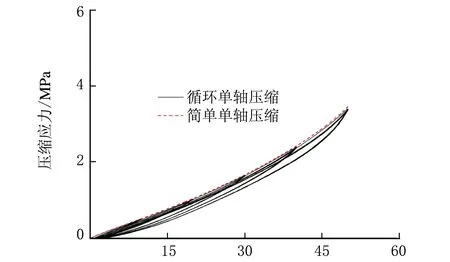
压缩应变/%(d) 30 phr CB
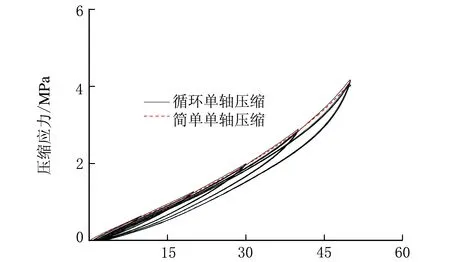
压缩应变/%(e) 40 phr CB

压缩应变/%(f) 50 phr CB图2 CB增强BR硫化胶的单轴压缩及单轴循环压缩应力-应变曲线
从图2可看出,纯BR硫化胶的压缩Mullins效应并不明显,加载-卸载循环的应力-应变曲线几乎重合;但CB的加入使BR硫化胶的Mullins效应增强,随着CB用量的增加,Mullins效应更加显著,具体表现在最大应力的明显下降。Rault等[7]认为,材料的异质性是导致Mullins效应产生的根本原因,异质性的增强将导致Mullins效应的强化,即异质性的程度是Mullins效应的“放大器”。
本研究中,相对于纯BR硫化胶,复合体系中的CB与BR硫化胶具有明显的异质性,且CB用量的增加使体系的异质性得以增强,从而使得Mullins效应得到强化。
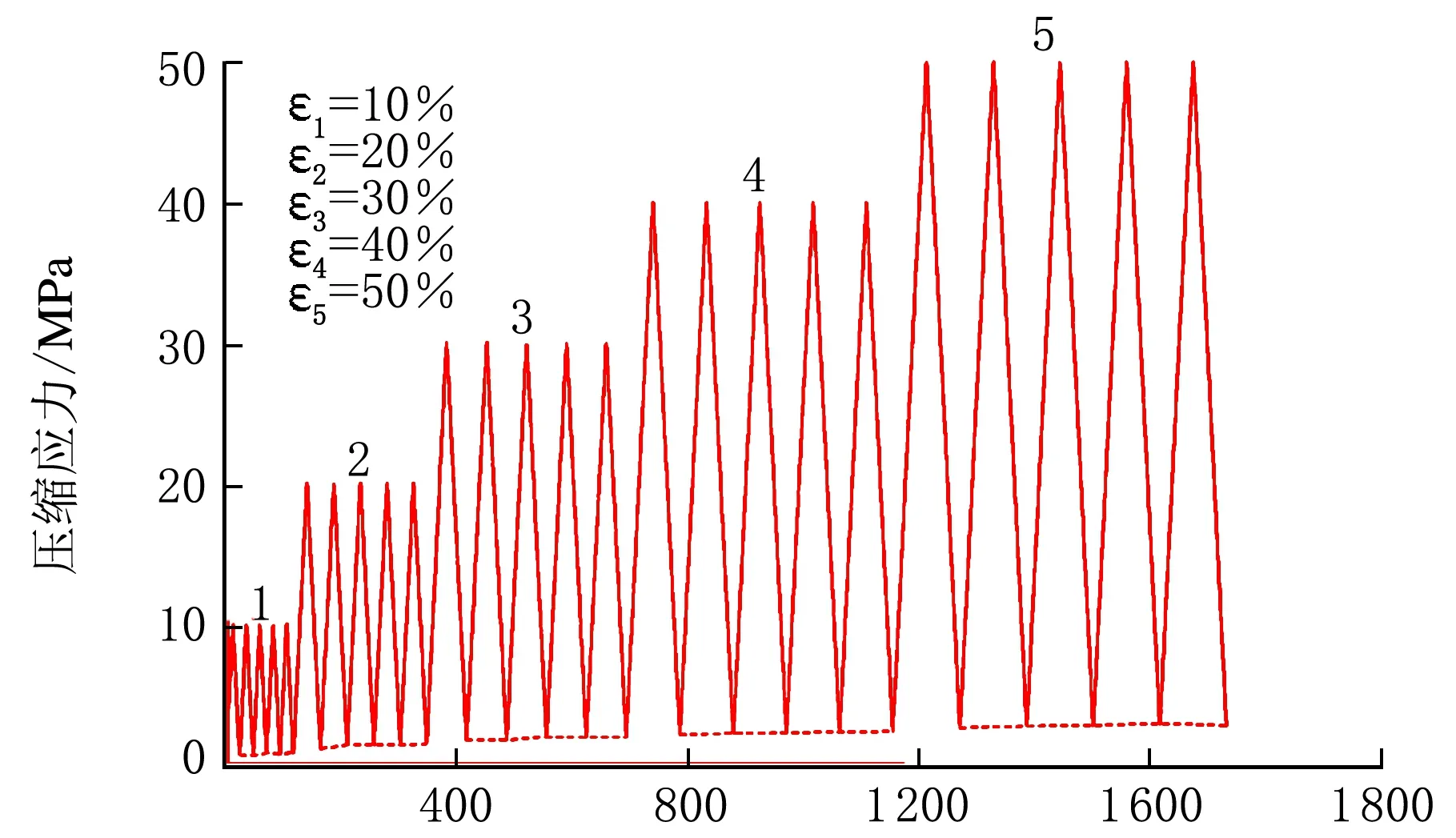
图3为不同用量CB增强BR硫化胶的单轴压缩及单轴循环压缩的应力-时间关系曲线。从图3可以看出,在特定的压缩应变下,第1次加载-卸载循环时,最大压缩应力达到最大值,随着压缩次数的增加,最大压缩应力缓慢下降;而且增大压缩应变,应力软化现象变得显著。对比图3可见,在特定压缩应变下,随着CB用量的增加,最大压缩应力下降幅度愈大,应力软化现象更为显著。为了更清楚地观察其Mullins效应引发的应力软化现象,将压缩应变为50 %时的应力-时间关系曲线放大并置于图3中左上角,通过局部放大图可清晰地发现,提高CB用量且提高应变,最大应力的降低更为明显,即CB的加入和大应变同时对BR硫化胶的Mullins效应起到了“放大器效应”。表2为图3中样品在50%压缩应变下的2次加载-卸载过程中的最大压缩应力,从表2可以看出CB增强BR体系的Mullins效应的“放大器效应”,表现在最大压缩应力的下降幅度上。

时间/s(a) 0 phr CB

时间/s(b) 10 phr CB

时间/s(c) 20 phr CB

时间/s(d) 30 phr CB
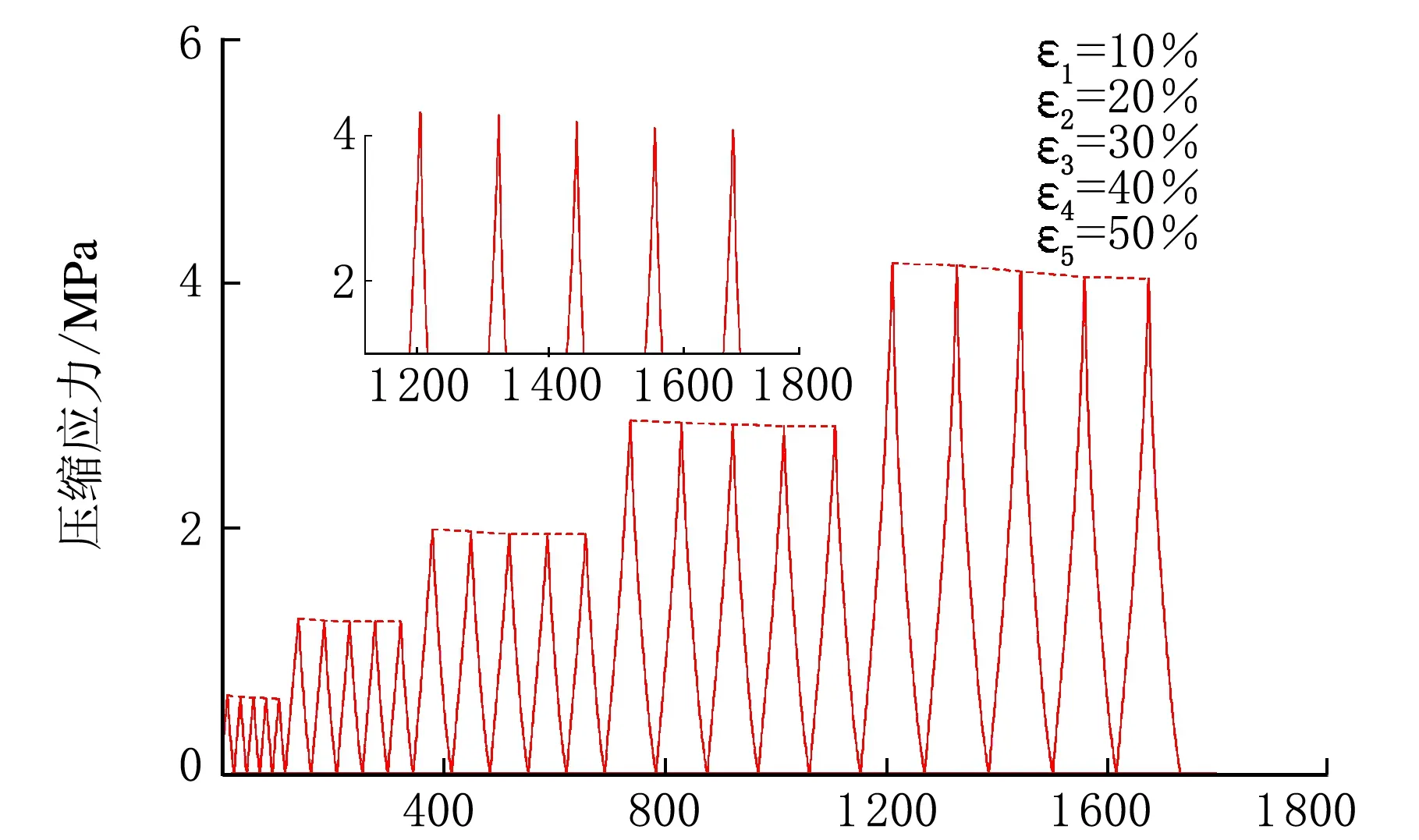
时间/s(e) 40 phr CB

时间/s(f) 50 phr CB图3 不同用量CB增强BR硫化胶的应力-时间曲线
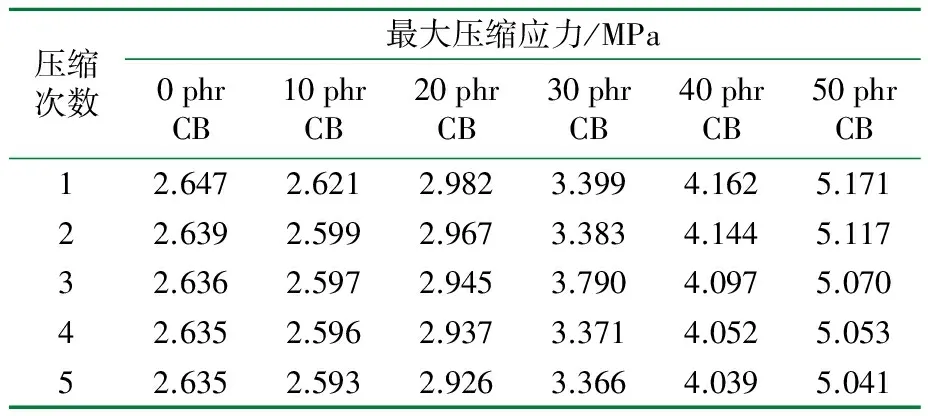
表2 样品在50%压缩应变下5次加载-卸载过程中的最大压缩应力
为了解释填充橡胶单轴压缩时的应力软化现象,Fukahori[8-9]提出双壳层模型来解释填充橡胶体系的增强和软化现象,在这一模型中,填料粒子表面有两层分别由不同运动状态的橡胶大分子构成的吸附层。紧邻填料粒子的内壳层的大分子处于玻璃态且分子运动受到了强烈的束缚;外壳层则为亚玻璃态,较未填充部分的硫化胶而言,外壳层分子也受到了高度的束缚。当填充粒子分散均匀时,外壳层是不连续的,与未填充的硫化胶形成“海-岛”结构[见图4(a)]。当试样初次压缩发生变形时,包裹填料粒子的吸附层橡胶相互靠近,外壳层结构发生取向和变形,最终与其它填料粒子的变形外壳层相互接触并形成了一个超级网络结构[见图4(b)]。结合Mullins与Tobin提出的物理模型[10],可以更好地解释填充橡胶的应力软化现象。对于发生应力软化的材料,其微观结构上可看作是由硬相与软相共同组成的复合体系,且材料的破坏程度取决于材料拉伸过程中的最大应变;一般说来,填充橡胶的强度是由硬相决定。本实验研究的CB增强硫化胶中,未填充的硫化胶为软相,填料粒子吸附层橡胶为硬相。在特定的压缩应变下初次压缩时,吸附层橡胶分子链受到严重束缚,在压缩过程中消耗了大部分能量;而当应力去除后,吸附层橡胶的变形仅部分恢复,残留变形较大,在相同压缩应变下的后续压缩循环中,吸附层橡胶对变形产生的应力较首次压缩减小,软相的变形贡献了大部分应力,因而压缩应力下降。在压缩应变增大时,吸附层橡胶产生了更大程度的变形,导致了最大压缩应力显著提高。
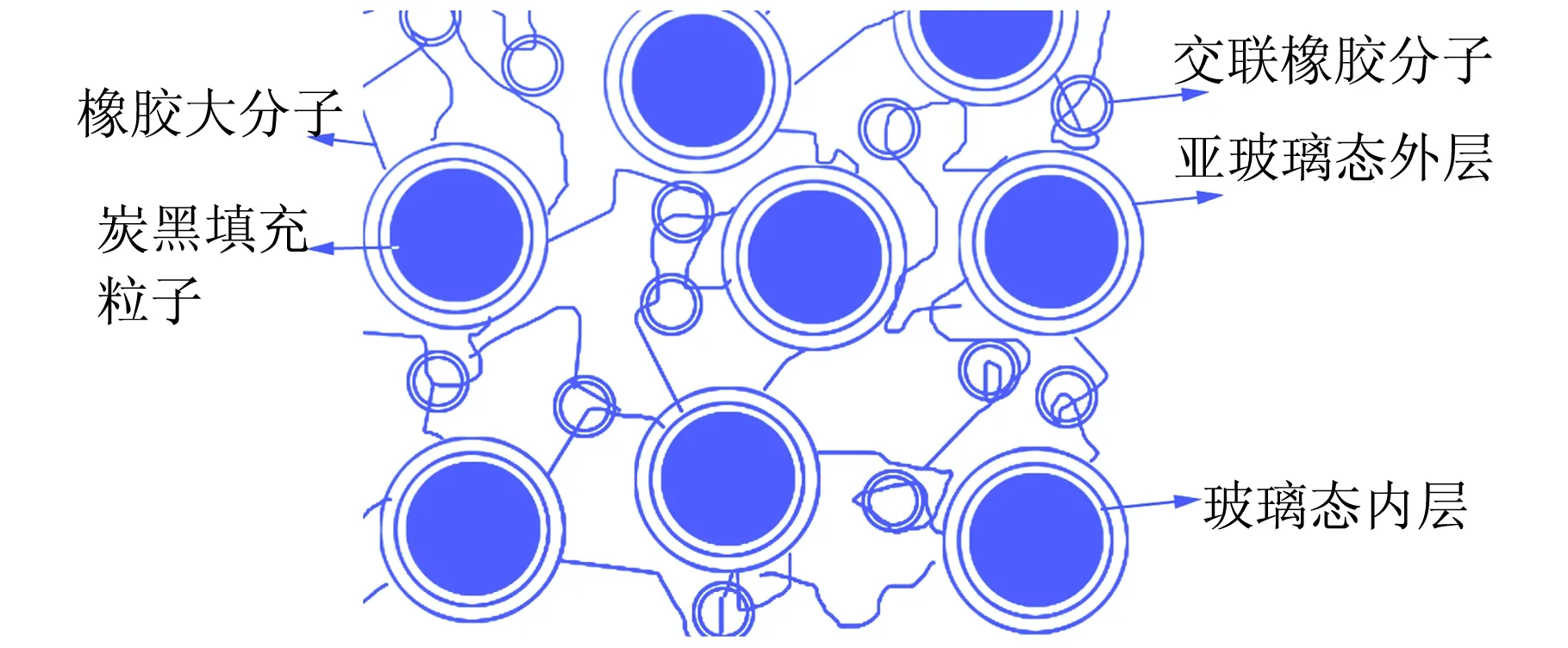
(a)

(b)图4 填充橡胶Mullins效应形成机制及恢复模型
图5为不同用量CB增强BR硫化胶的单轴循环压缩瞬时残留变形。

时间/s(a) 0 phr CB
时间/s(b) 10 phr CB

时间/s(c) 20 phr CB

时间/s(d) 30 phr CB
时间/s(e) 40 phr CB
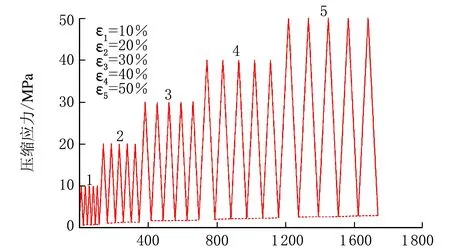
时间/s(f) 50 phr CB图5 不同用量CB增强BR硫化胶的应力-时间曲线
从图5可看出,在特定压缩应变下,随着压缩次数增加,瞬时压缩残留变形缓慢增加;但当压缩应变增大时,瞬时残留变形发生大幅增加。随着CB用量的提高,在特定应变下的瞬时压缩残留变形增加的幅度逐渐变大。
综上可见,CB的加入使BR硫化胶的力学性能得到了增强,强化了体系压缩模式下的Mullins效应,发挥了“放大器”作用,并表现在体系应力软化的加剧以及瞬时压缩残留变形的增大。
3 结 论
(1) CB增强BR硫化胶的强度较纯BR硫化胶显著提高,且CB用量为40 phr时,力学性能较好。
(2) CB增强BR体系在单轴循环压缩过程中存在显著的Mullins效应,提高CB用量及增大压缩应变,Mullins效应得到强化,CB用量和压缩应变的增大起到了Mullins效应的“放大器”作用。
(3) 对于CB增强BR硫化胶的压缩Mullins效应,在特定压缩应变下,最大压缩应力在第1次加载-卸载循环中达到最大值,在之后的压缩循环中有所下降;随着压缩应变及压缩次数的增加,瞬时残留压缩变形增大。
参 考 文 献:
[1] 张艺馨,于文娟,王兆波.BR/EVA/HIPS TPV的制备和性能研究[J].橡胶工业,2011,58(10):596-600.
[2] 史新妍,张萍,黄玉华,等.BR9002的性能研究[J].橡胶工业,2006,53(8):471-475.
[3] MULLINS L.Softening of rubber by deformation[J].Rubber Chemistry and Technology,1969,42(1):339-362.
[4] HOUWINK R.Slipping of molecules during the deformation of reinforced rubber [J].Rubber Chemistry Technology,1956,29(3):888-893.
[5] HANSON D E,HAWLEY M,HOULTON R,et al.Stress softening experiments in silica-filled polydimethylsiloxane provide insight into a mechanism for the Mullins effect [J].Polymer,2005,46(24):10989-10995.
[6] DIANI J,FAYOLLE B,GILORMINI P.A review on the Mullins effect[J].European Polymer Journal,2009,45(3):601-612.
[7] RAULT J,MARCHAL J,JUDEINSTEIN P,et al.Stress-induced crystallization and reinforcement in filled natural rubbers:2H NMR study[J].Macromolecules,2006,39(24):8356-8368.
[8] FUKAHORI Y.New progress in the theory and model of carbon black reinforcement of elastomers[J].Journal of Applied Polyer Science,2005,95(1):60-67.
[9] FUKAHORI Y.Generalized concept of the reinforcement of elastomers.Part 1:Carbon black reinforcement of rubbers[J].Rubber Chemistry and Technology,2007,80(4):701-725.
[10] MULLINS L,TOBIN N R.Theoretical model for the elastic behavior of filler-reinforced vulcanized rubbers[J].Rubber Chemistry and Technology,1957,30(2):555-571.
