一种新的基于四维忆阻超混沌系统的医学图像加密算法研究

柴秀丽+++程云龙

摘 要： 基于低维混沌系统的图像加密算法存在密钥空间小、安全性不高等问题。为此，在三维Cai混沌系统的基础上，构造出一个四维忆阻超混沌系统，同时，基于该系统提出一种新的医学图像加密算法。安全性分析结果表明，算法密钥空间大，对密钥非常敏感，能够抵抗蛮力攻击、已知（选择）明文攻击和差分攻击。

关键词： 四维忆阻超混沌系统； 混沌； 医学图像加密； Lyapunov指数

中图分类号：TP391 文献标志码：A 文章编号：1006-8228（2016）05-21-03

Abstract： The image encryption algorithm based on low dimensional chaotic system has the problems of the key space small and the security not high. Therefore， on the basis of three dimensional Cai system， a four-dimensional memristive hyperchaotic system was constructed， and further a new medical image encryption algorithm is proposed. The security analysis shows that the algorithm has a large key space， is very sensitive to keys， and can resist the brute force attack， known plaintext attack， chosen plaintext attack and differential cryptanalysis attack.

Key words： four dimensional memristive hyperchaotic systems； chaos； medical image encryption； Lyapunov exponents

0 引言

随着网络和多媒体技术的进步，图像信息的安全问题[1]成为现在密码学研究的重点之一，特别是医学图像[2-4]具有高分辨率、高精度、大数据量和同色像素连续性高等特点，其安全性隐患成为制约远程医疗和远程监护系统发展的重点问题。混沌系统[5]对参数和初始值的高度敏感性等特性很好地对应于密码学的要求，为图像加密提供了新思路。在混沌[6-8]密码学研究中，低维混沌系统可提供的密钥空间较小，抗攻击性能弱[9-10]；高维混沌系统具有的密钥空间更大，拓扑结构和非线性动力学行为更为复杂，轨迹更加难以预测和攻破[11-12]。由忆阻器构造出的系统具有更为复杂的拓扑结构[13-14]，相对于一般的混沌系统具有更为复杂的动力学行为，为设计高安全的混沌图像加密算法提供了支持[15]。

本文通过结合忆阻器和Cai混沌系统，构造出一个新的四维忆阻超混沌系统，并设计了一种保密性更强的医学图像加密算法。

1 四维忆阻超混沌系统

无量纲处理后的状态方程可表达为⑴：

⑴

其中x，y表示电容，z表示电流，w表示磁通量，w（Φ）=a+3bΦ2，表示忆阻器状态，a=1/7，b=2/7，系统参数α=10，β=9/7，γ=100/7，ξ=0.1。

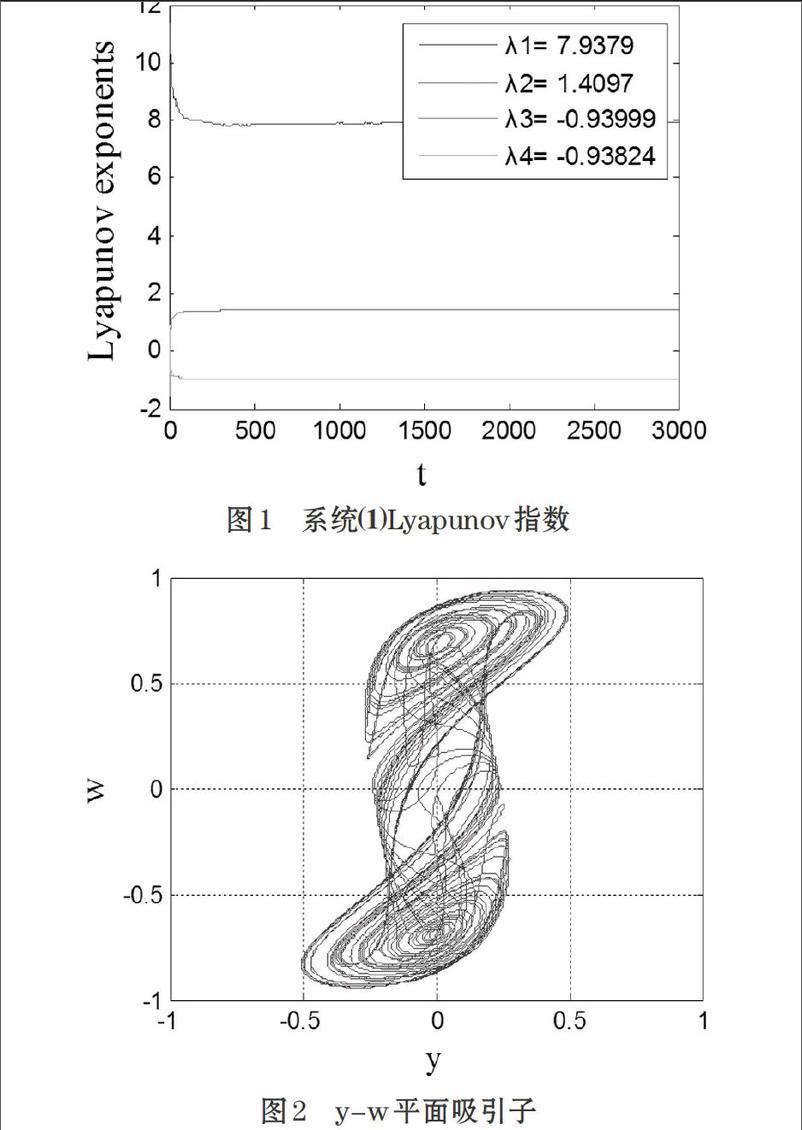
使用Wolf算法计算式⑴的Lyapunov指数，当α=10，β=9/7，γ=100/7，ξ=0.1时，式⑴的Lyapunov指数如图1所示。有2个大于0的Lyapunov指数λ1=7.9379，λ2=1.4097，此时式⑴产生了超混沌运动，称为四阶忆阻超混沌系统。图1所示为系统产生混沌序列的时间轨迹，图2为系统的吸引子曲线。

<2 医学图像加密算法

加密过程如图3所示。

[明文][密钥][忆阻超混沌系统] [扩散][扩散][扩散] [扰动] [密文] [n轮循环]

图3 加密过程

加密步骤如下：

Step1 设明文图像M，大小为m×n，将M转换成一维序列P（大小为1×mn），由公式⑵和⑶计算出扰动参数p和预迭代次数K，其中ceil表示向上取整。

⑵

⑶

Step2 设系统参数α=10，β=9/7，γ=100/7，ξ=0.1和初值x=10-10，y=0，z=0，w=p/10^8，迭代K次，生成x，y，z，w，4个序列。

Step3 分别取x，y序列中第{1001，1002，...，K}项，然后合并，取{1，2，...，m×n}项作为序列F，并对序列中元素按照式⑷进行处理，使其值在0-255内。

⑷

其中，F（i）代表序列中的第i个元素。

Step4 按式⑸对明文序列P进行第一次扩散操作，即P中第i个元素P（i）和序列F中第i个元素F（i）进行异或操作，得到扩散序列P1。

⑸

此处，p1（i）代表序列P1中的第i个元素。

Step5 对序列F行升序排序，同时记录元素位置，生成新的位置序列D，PP（Di）=P1（i）i。

以式⑹对明文进行置乱操作，即P1中第i个像素值放在向量PP中第Di的位置上，得到置乱后序列PP。

Step6 分别取z，w序列中第{1001，1002，...，K}项，合并，取{1，2，...，m×n}项作为二次扩散序列F1，按式⑷进行处理，使得F的元素值在0-255范围内，然后按式⑸对置乱后序列PP进行第二次扩散操作，得到密文序列C1，然后把序列重组为大小为m×n的图像。

Step7 为了达到更好的加密效果，重复Step1-Step6进行多轮加密，得到最终密文C，加密过程结束。

解密过程为加密的逆过程，在系统参数和初值一致时，可得与明文完全相同的解密图像。

3 实验结果及安全性分析

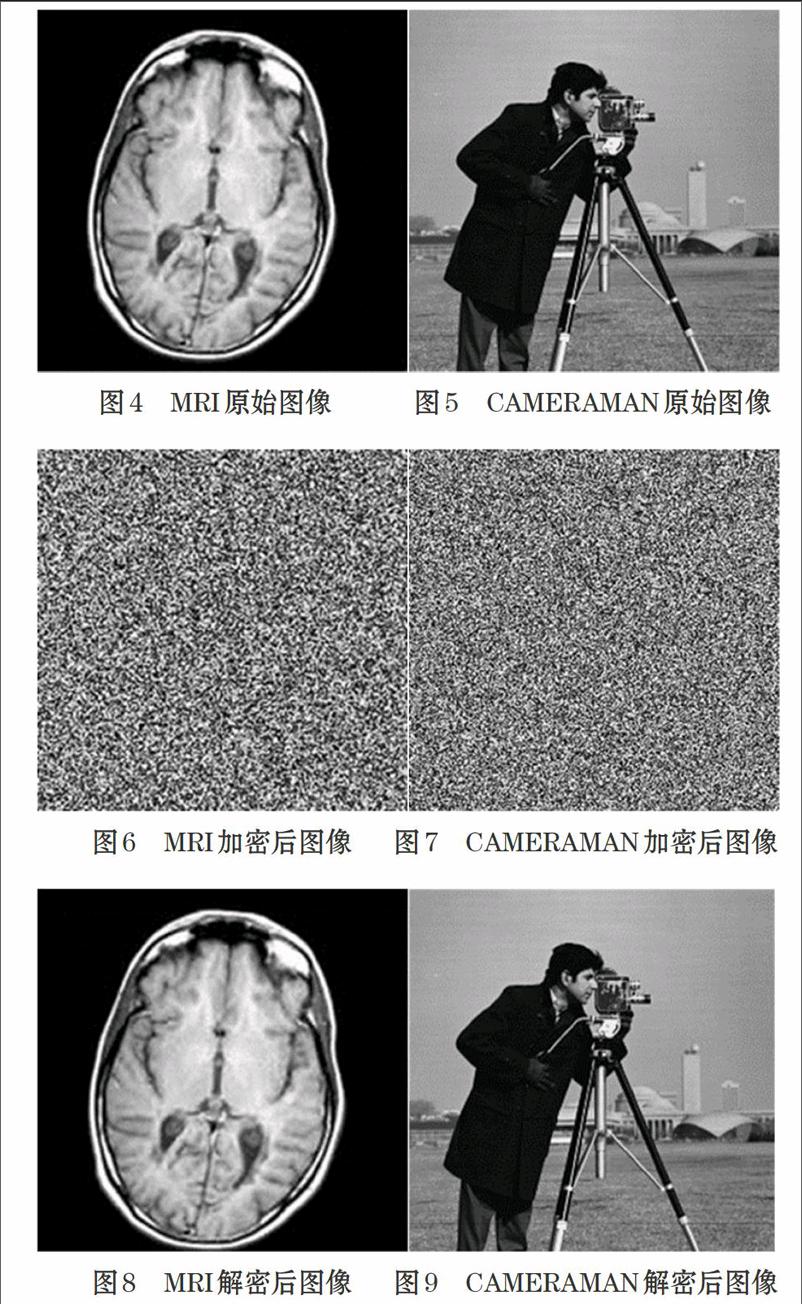
分析加密算法时，安全性是首要考虑的问题[6]，下面对本文加密算法的安全性进行验证分析。实验采用一副186×190像素的灰度级MRI脑部图像和一副256×256的CAMERAMAN图像，将其作为待加密图像，如图4和图5所示，系统参数α=10，β=9/7，γ=100/7，ξ=0.1和初值[x，y，z，w]=[10-10，0，0，0]，加密后密文如图6和图7所示，以相同的密钥解密后的图像如图8、图9所示。

优良的加密算法应该对密钥敏感，并且密钥空间应该足够大，以抵抗穷举攻击[9]。

本文密钥包括混沌系统4个初始值和4个系统参数，设计算机精度为1014，则本文算法的密钥空间为108×14≈2375。表1给出不同加密算法的密钥空间对比。

表1 不同算法的密钥空间对比

[算法＼&密钥空间＼&文献[16]＼&1.2×1024＼&文献[17]＼&1084＼&文献[18]＼&1056＼&文献[19]＼&9.8×1055＼&本文算法＼&10112＼&]

可以看出，本文所提出的加密算法密钥空间远大于2100，且较其他文献加密算法的密钥空间更有优势，因此能够更好的抵御蛮力攻击。

4 结束语

本文提出了一种基于忆阻混沌系统的医学图像加密算法，采用扩散-置乱-扩散的加密模式，实验和仿真分析表明，该算法具有如下特点：密钥空间大，足以抵抗蛮力攻击；密文图像像素均匀分布，抵抗统计攻击能力强；密钥敏感性高；可以有效抵抗差分攻击。

因此，本文提出的加密算法安全高效，在远程医学、卫星、遥感等图像信息安全通信领域具有很大的应用前景。

参考文献（References）：

[1] A.Kanso， M.Ghebleh.An efficient and robust imageencryption scheme for medical applications[J].Commun Nonlinear Sci Numer Simulat，2015.24（3）：98-116

[2] Chong Fu， Wei-hong Meng， Yong-feng Zhan.An efficientand secure medical image protection scheme based on chaotic maps[J]. Computers in Biology and Medicine，2013.43（11）：1000-1010

[3] J B.Lima， F.Madeiro， F.J.R.Sales. Encryption of medicalimages based on thecosine number transform[J].Image Communication，2015.35（5）：1-8

[4] Li-bo Zhang， Zhi-liang Zhu， Ben-qiang Yang. MedicalImage Encryption and Compression Scheme Using Compressive Sensing and Pixel Swapping Based Permutation Approach[J].Hindawi Publishing Corporation. Mathematical Problems in Engineering，2015.11（2）：1-9

[5] AlvarezG， LiShujun. Some Basic Cryptographic Require-ments for Chaos-based Cryptosystems[J].International Journal of Bifurcation and Chaos，2006.16（8）：1-12

[6] Ailong Wu， Shiping Wen， Zhigang Zeng. Synchronizationcontrol of a class of memristor-based recurrent neural network[J].Information Sciences，2012.183（11）：106-116

[7] 武花干，陈胜垚，包伯成.忆阻混沌系统的脉冲同步与初值影响研究[J].物理学报，2015.64（3）：1-8

[8] 章秀君，吴志强，方正.一种基于四维超混沌系统的数字图像加密算法[J].计算机工程，2013.39（8）：169-172

[9] 赵玉青.基于改进Chen混沌系统的图像加密算法[J].小型微型计算机系统，2014.35（9）：2162-2166

[10] 朱志良，卜超，刘洪娟等.一种结合混沌映射的Enigma加密方案[J].小型微型计算机系统，2012.33（11）：2503-2507

[11] 刘玉东，王连明.基于忆阻器的spiking神经网络在图像边缘提取中的应用[J].物理学报，2014.63（8）：1-7

[12] 蒋君莉，张雪锋.基于超混沌序列的Feistel 结构图像加密算法[J].计算机应用研究，2014.31（4）：1199-1204

[13] 肖烈虹，江贵平.基于高维混沌序列的医学图像加密[J].中国医学物理学杂志，2009.26（3）：1180-1182

[14] 王玲玲，武怀勤，丁三波等.具有脉冲的忆阻器神经网络周期解的稳定性[J].郑州大学学报，2014.46（6）：31-42

[15] 李志军，曾以成.基于文氏振荡器的忆阻混沌电路[J].电子与信息学报，2014.36（1）：88-93

[16] Pisarchik A， Zanin M （2008） Image encryption withchaotically coupled chaotic maps， Phys D 237（20）：2638-2648

[17] Zhang Q， Liu L， Wei X .Improved algorithm for imageencryption based on DNA encoding and multichaotic maps， Int J Electron Commun （AE?），2014.68：186-192

[18] Yang H， Wong K W， Liao X， Zhang W， et al.A fast imageencryption and authentication scheme based on chaotic maps， Commun Nonlinear Sci Numer Simul，2010.15：3507-3517

[19] Sun F， Liu S， Li Z， Lu Z .A novel image encryptionscheme based on spatial chaos map， Chaos Solit Fract，2008.38：631-640