两房室神经元模型的同步簇放电的动力学分析*

孟盼陆启韶赵勇董健卫

（1.广东药科大学基础学院，广州 510006）（2.北京航空航天大学航空科学与工程学院，北京 100191）（3.河南理工大学数学与信息科学学院，焦作 454000）

两房室神经元模型的同步簇放电的动力学分析*

孟盼1†陆启韶2赵勇3董健卫1

（1.广东药科大学基础学院，广州 510006）（2.北京航空航天大学航空科学与工程学院，北京 100191）（3.河南理工大学数学与信息科学学院，焦作 454000）

研究一个具有电流反馈的两房室锥体神经元的簇放电动力学问题.首先，利用数值模拟研究了该神经元的树突和胞体两个房室之间的峰相位同步行为.其次，基于快慢动力学分析方法，给出了快子系统的双参数分岔曲线图，结果表明快子系统产生了3个余维-2分岔点，它们分别为fold-Hopf分岔点ZH、Cusp分岔点CP和Bogdanov-Takens分岔点BT.最后，根据这些余维-2分岔点确定系统存在着丰富的簇放电模式，如“fold/fold”型，“Hopf/Hopf”型，“Hopf/homoclinic”型以“fold/homoclinic”型簇振荡等，并分析研究了簇放电模式的产生以及它们之间相互转迁的动力学机理.本文的研究结果进一步表明了神经元的几何形态特性对于神经元放电模式多样性的重要影响.

簇放电， 同步， 电流反馈， 快慢动力学分析， 分岔

引言

神经元作为神经系统的基本功能单位，通过放电活动感受外界刺激，从而实现神经信息的传递［1］.不同的放电模式是对不同外界刺激的不同反映［2-3］.研究表明，簇放电（bursting）是神经元最重要的放电模式之一，在生物信息编码中起着关键作用.簇振荡比单个峰放电（spiking）可以携带更多的信息并且更加可靠，因此理解簇振荡活动的产生和转迁机制具有重要意义［4］.簇振荡表现为慢变量引起的静息态（silent phase）与快变量引起的重复放电状态（active phase）之间的相互转迁.利用快慢动力学分析来考察簇放电的静息态和放电状态之间的分岔，并依此给出簇模式的拓扑类型，是理解簇振荡产生机理的主要方法［5］.

为了更好的探究神经元的各部分在信息传递中的作用，神经元的形态结构多利用房室模型来刻画，如锥体神经元［6］，蒲肯野神经元［7］和中间神经元［8］等.房室模型是将空间上连续的单个神经元分成离散的多个房室，各个房室相互连接后整体描述神经元的时空变化.和单房室神经元模型相比，多房室模型同样可以产生丰富的放电模式，并且能够更好的体现神经元的形态结构特征［6-8］.利用房室模型来研究神经元的电活动行为，一直是计算神经领域的热点.本文主要研究具有电流反馈的两房室锥体神经元模型，通过数值模拟和理论分析，讨论了神经元通过形态参数变化时展现的放电节律模式以及各种模式之间的相互转迁机理.

1 模型描述

考虑锥体神经元，它由树突和轴突两个房室构成.模型描述如下［9］：

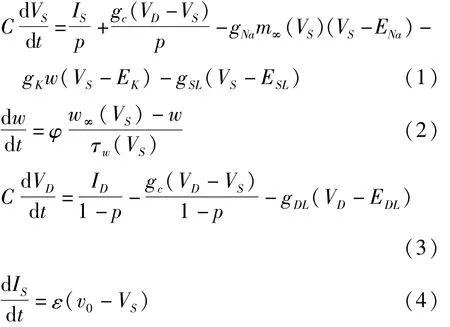
其中门控函数为：

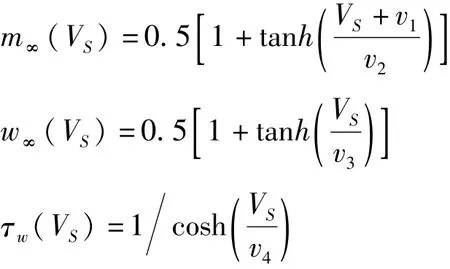
（1）式和（3）式分别为胞体膜电压VS和树突膜电压VD的动力学方程，其中胞体房室的电流包含了胞体的突触输入电流、树突流向胞体的内部电流、Na+离子电流、K+离子电流和泄漏电流；树突房室的电流包含了树突的突触输入电流、树突流向胞体的内部电流和泄漏电流.ENa和EK分别表示Na+离子通道和K+离子通道的平衡电位，ESL和EDL分别为胞体和树突膜上泄漏电流的平衡电位；gNa、gK、gSL和gDL分别代表各通道的最大电导；gc表示两房室连接电导；C表示膜电容；IS和ID分别为胞体和树突的突触输入电流；p和1-p分别表示胞体和树突所占的面积比例.p是锥体神经元的一个重要几何形态参数.（2）式描述了K+离子通道门开通概率w的变化规律.作为外界电流刺激的影响，（1）式中的胞体突触输入电流IS由一个线性反馈的动力学方程（4）支配，这里ε是时间尺度因子，取为很小的正数以保证IS的慢变性.方程（1）-（4）称为具有电流反馈的两房室神经元模型.由于ε≪1，因此方程（1）-（3）可视为快子系统，其中取IS作为慢变量，p作为控制参数.在这篇文章中，其它参数取值为：ε＝0.01，gNa＝50，gK＝15，gSL＝2，gDL＝2，gc＝2，ENa＝10，EK＝-90，ESL＝-70，EDL＝-70，Φ＝0.3，C＝2，v0＝-22，v1＝1.2，v2＝18，v3＝10，v4＝6.

为了便于以后的研究，先考虑在上述参数条件下两个房室的同步动力学行为.引入峰相位函数φS（t）［10］，定义为：

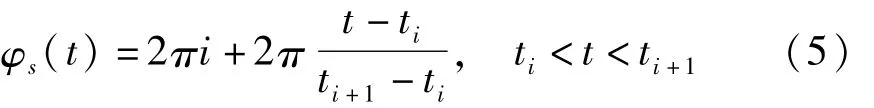
其中ti是第i次峰放电发放的时间.因此每经过一次峰放电，峰相位就增加2π.基于相位函数的定义，引入频率函数ω（t）＝˙φ（t）和平均峰频率函数Ω（t）＝＜˙φ（t）＞，这里＜·＞表示对时间取平均，因此有

如果两个房室的平均峰频率差ΔΩ＝ΩS-ΩD为0，那么两个房室的放电频率一致（在时间平均的意义上），从而实现放电相位的同步［11］.

2 神经元形态参数引起的两室间簇放电的同步

通过数值计算得到ΔΩ和形态参数p的关系图（见图1）.由图1可以看出在0.18＜p＜1.0的参数范围内有平均峰频率差ΔΩ＝0，即两个房室总是处于峰相位同步状态，下面的图3～6的数值结果也证实这一点.因此在下面的神经元簇放电模式研究中，我们可以着重考察其中一个房室（如胞体）的放电动力学行为，例如只依据VS的分岔图就可以进行快慢动力学分析.

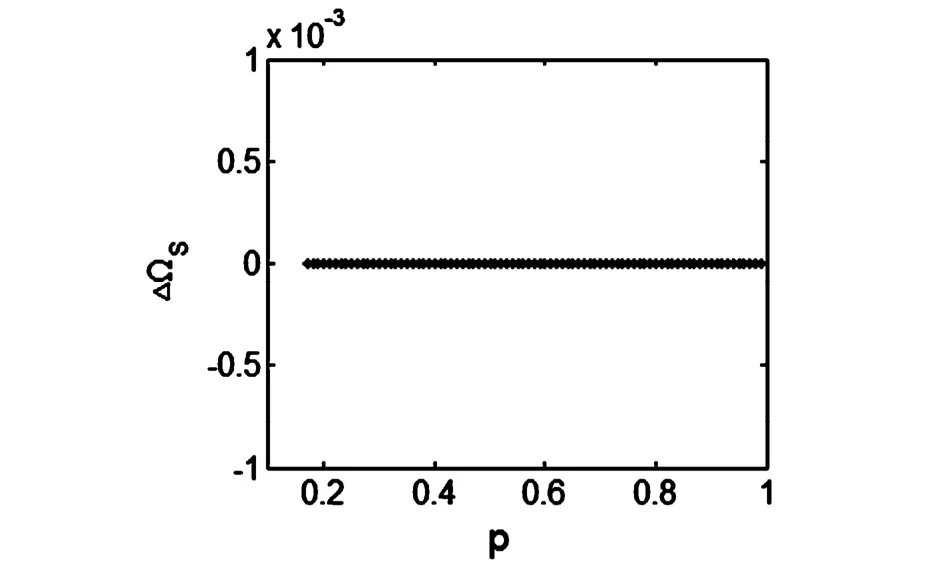
图1 平均峰频率差ΔΩ关于p的变化图Fig.1 Relationship of themean spike frequency differenceΔΩ and parameter p

3 簇放电模式及转迁

现在考虑前述的两房室锥体神经元模型的复杂放电模式，图2给出一些分岔结果（具体的分析过程从略）.图2（a）是全系统（1）-（4）关于形态参数p的分岔图.可以看出，平衡点的分岔曲线是一条直线，在HB处出现supHopf分岔，系统的静息态消失，使得稳定平衡点变为不稳定，同时产生稳定极限环，系统开始振荡.图2（b）是双参数（IS，p）-平面的分岔曲线图.其中余维-1分岔曲线包括Hopf分岔曲线（h），平衡点的鞍结分岔曲线（f1，f2），同宿轨分岔曲线（hc）.余维-2分岔点分别为fold-hopf分岔点ZH（Hopf分岔曲线h和鞍结分岔曲线f2的交点）、Bogdanov-Takens分岔点BT（fold分岔曲线f1和同宿轨分岔曲线hc相切的点）以及Cusp分岔点CP（两条鞍结分岔曲线f1和f2处的交点）.左下角是点BT附近的局部放大图.右上角是点ZH附近的局部放大图，右下角是点CP附近的放大图.

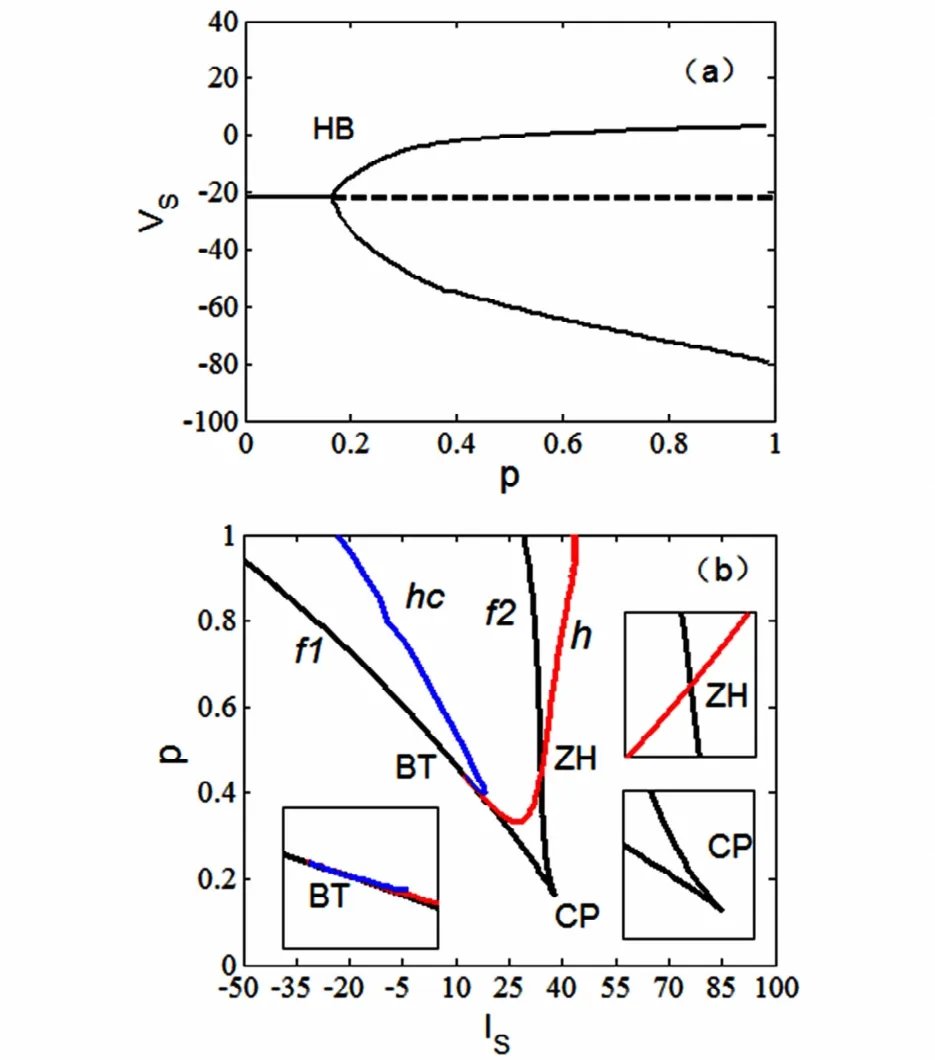
图2 （a）全系统（1）-（4）关于形态参数p的分岔图.（b）（IS，p）-参数平面上快子系统（1）-（3）的分岔曲线.Fig.2 （a）One-parameter bifurcation diagram of the whole system with the variation of parameter p.（b）Bifurcation curves in（IS，p）-parametric plane for the fast subsystem（1）-（3）

为了进一步说明问题，下面结合图2来考虑形态参数p的变化对系统（1）-（4）的影响.通过取参数p不同的值来给出整个系统的某些典型的放电模式.随着参数p的变化，系统呈现不同形式的簇放电模式，如图3～6所示，其中黑线和红线分别表示胞体和树突的放电时间序列图.可以看到这两个房室的簇放电行为一直处于峰相位同步状态.接下来利用快慢动力学分析，解释这些簇模式之间转迁的动力学机理.

首先，当形态参数p＝0.19时，系统产生簇放电模式，如图3（a）所示.快慢动力学分析如图3（a）所示.快子系统的分岔曲线是一条S形曲线，上支由稳定焦点（实线）和不稳定焦点（虚线）组成；中支是由鞍点（虚线）组成；下支是由稳定结点（实线）组成.由图2（b）可以看出，现在在慢变参数区域内的快子系统的分岔曲线从左到右仅有平衡点的鞍结分岔曲线f1和f2，相应的快子系统的分岔点分别记为F1和F2.全系统的轨线也叠加在快子系统的分岔图上.随着参数IS的增加，相应于快子系统分岔曲线下支稳定结点的簇放电的静息态，经鞍结分岔F2转迁到上支的放电状态.随着IS的减小，放电状态经由鞍结分岔F1转迁到下支的静息态.因此簇放电类型是“fold/fold”型簇放电［5］.

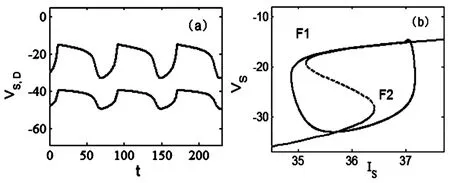
图3 当p＝0.19时，“fold/fold”型簇放电.（a）两个房室的膜电位VS（黑线），VD（红线）的时间历程图.（b）快慢动力学分岔分析.Fig.3 Bursting of“fold/fold”type when p＝0.19.（a）Time history ofmembrane potentials VSin the black line and VDin the red one.（b）Fast-slow dynamics of the fast subsystem.

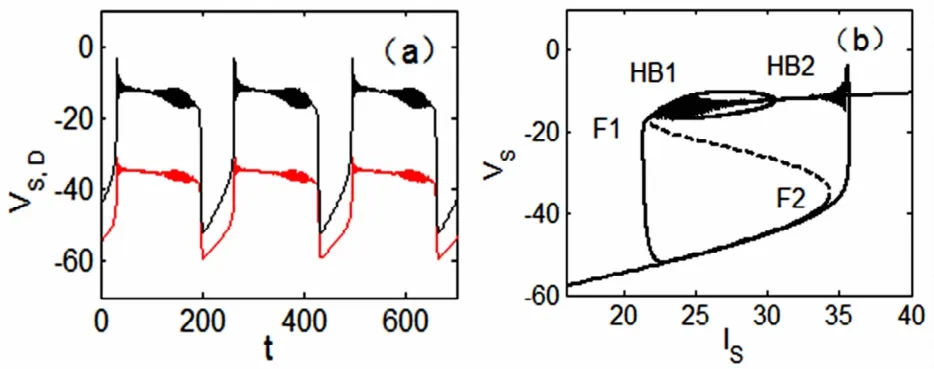
图4 当p＝0.35时，“Hopf/Hopf”型簇放电.（a）两个房室的膜电位VS（黑线），VD（红线）的时间历程图.（b）快慢动力学分岔分析.Fig.4 Bursting of“fold/fold”type when p＝0.35.（a）Time history ofmembrane potentials VSin the black line and VDin the red one.（b）Fast-slow dynamics of the fast subsystem

其次，当p＝0.35时，系统可产生如图4（a）的簇放电模式.运用图4（b）的快慢动力学分析，来研究此放电的动力学性质及其类型.通过双参数（IS，p）-平面分岔图2（b）可以看出，在两个鞍结分岔点F1和F2之间，产生了两个supHopf分岔点，在快子系统的分岔图上分别记为HB1和HB2.这样，S形分岔曲线的上支的稳定焦点（实线）经由点HB1处的Hopf分岔而失稳（虚线），同时产生稳定极限环.随着参数IS的增加，该稳定极限环经由点HB2处的Hopf分岔消失而转变为稳定焦点.现在结合全系统的轨线来讨论簇放电的产生过程.随着慢变量IS的增加，由于supHopf分岔点HB2处的慢变效应［11］，下支的静息状态转迁到上支的放电状态；随着慢变量IS的减小，放电状态收敛于经由supHopf分岔点HB1产生的稳定焦点，再经由鞍结分岔F1转迁到下支的静息状态.这种簇振荡模式称为“Hopf/Hopf”型簇放电［5］.综上所述，当参数p的取值小于余维-2分岔点BT的纵坐标pBT值时，系统会产生“fold/fold”型或“Hopf/Hopf”型簇放电.

接下来，当形态参数p的取值位于两个余维-2分岔点Bogdanov-Takens分岔点BT和fold-hopf分岔点ZH的纵坐标值之间，例如p＝0.42时，两个房室的簇放电模式如图5（a）所示，其相应的分岔分析见图5（b）.和图4（b）相比，现在快子系统仅有一个SupHopf分岔点HB.神经元的静息态经由SupHopf分岔而转迁到放电态，放电态又经极限环的同宿轨分岔HC转变为静息态，从而形成了一个“Hopf/Homoclinic”型簇放电［5］.

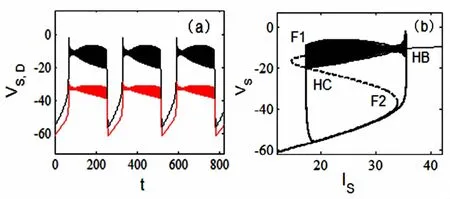
图5 当p＝0.42时，“Hopf/Homoclinic”型簇放电.（a）两个房室的膜电位VS（黑线）、VD（红线）的时间历程图.（b）快慢动力学分岔分析.Fig.5 Bursting of“Hopf/Homoclinic”type when p＝0.42.（a）Time history ofmembrane potentials VSin the black line and VDin the red one，（b）Fast-slow dynamics of the fast subsystem.

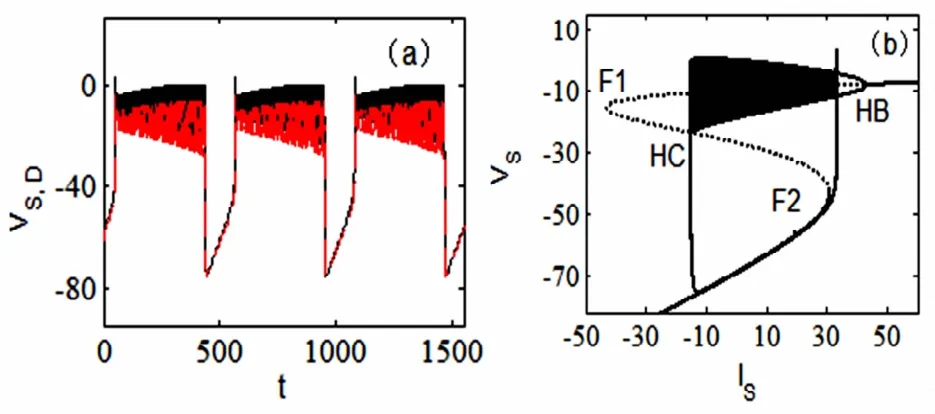
图6 当p＝0.9时，“fold/homoclinic”型簇放电.（a）两个房室的膜电位VS（黑线）、VD（红线）的时间历程图.（b）快慢动力学分岔分析.Fig.6 Bursting of“fold/Homoclinic”type when p＝0.9，（a）Time history ofmembrane potentials VSin the black line and VDin the red one.（b）Fast-slow dynamics of the fast subsystem.

最后，当形态参数p的取值大于余维-2分岔点fold-hopf分岔点ZH的纵坐标pZH值，例如p＝0.9时，系统可产生如图6（a）的簇放电模式，相应的快慢动力学分析如图6（b）所示.随着慢变量的增加，快子系统依次经过鞍结分岔F1、同宿轨分岔HC、鞍结分岔F2、supHopf分岔HB.值得注意的是，现在鞍结分岔点F2和supHopf分岔点HB的先后顺序和图5（b）有所不同.因此，系统轨线的静息态由平衡点的鞍结分岔（F2）转变为放电状态，然后放电状态沿着由HB产生的稳定极限环运动，最后消失于极限环的同宿轨分岔（HC）.这种簇振荡模式称为“fold/homoclinic”型簇放电［5］.

4 结论

通过数值模拟和快慢动力学分析，研究了具有电流反馈的两房室锥体神经元的簇放电模式.结果表明，胞体和树突这两个房室在一定条件下可以处于峰相位同步状态：神经元可以表现出丰富的放电模式，如“fold/fold”型、“Hopf/Hopf”型、“Hopf/Homoclinic”型和“fold/homoclinic”型簇放电模式；特别地，神经元的几何形态参数对神经元放电节律的产生和转迁有着重要的影响.还注意到，如果不考虑电流反馈的话，此两房室神经元模型并不存在这些丰富的簇放电模式，因此本文的研究对进一步揭示外界激励对神经元放电活动的重要作用也有一定意义.

1 汪云九.神经信息学-神经系统的理论和模型.北京，高等教育出版社，2006（Wang Y J.Neuro-informationtics：theories and models of neural systems.Beijing：Higher Education Press，2006（in Chinese））

2 Fan Y S，Chay T R.Generation of periodic and chaotic bursting in an excitable cellmodel.Biological Gybernetics，1994，71（5）：417～431

3 Gu H G，Pan B B.Identification of neural firing patterns，frequency and temporal coding mechanisms in individual aortic baroreceptors.Frontiers in Computational Neuroscience，2015，9：108

4 Lisman JE.Bursts as a unit of neural information：making unreliable synapses reliable.Trends in Neuroscience，1997，20（1）：38～43

5 Rinzel J.Bursting oscillations in an excitable membranemodel.In：Ordinary and Partial Differential Equations，Lecture Notes in Mathematics.edited by Sleeman B D，Jarvis R J，New York：Springer，1995：304～316

6 马丹，刘深泉，汪雷.两房室神经元模型的分岔现象.北京生物医学工程，2011，30（6）：567～573（Ma d，Liu S Q，Wang L.Bifurcation phenomenon in a two-compartment neuron model.Beijing Biomedical Engineering，2011，30（6）：567～573（in Chinese））

7 张煦晨，刘深泉，任会霞.浦肯野神经元回路中的同步性研究.动力学与控制学报，2015，13（5）：377～381（Zhang X C，Liu SQ，Ren H X.The research on synchronization in purinje neural circuit.Journal of Dynamics and Control，2015，13（5）：377～381（in Chinese））

8 江小芳，刘深泉，张煦晨.中等多棘神经元的多房室模型分析.生物物理学报，2013，29（7）：527～542（Jiang X F，Liu SQ，Zhang X C.Multi-compartmentmodelanalysis of the medium spiny neuron.Biphysics Reports，2013，29（7）：527～542（in Chinese））

9 伊国胜，王江，魏熙乐，邓斌.电场调制神经元放电动力学的生物物理机制.中国科学：物理学·力学·天文学，2013，42（2）：210～216.（Yin G S，Wang J，Wei X L，Deng B.The mechanism of electrical field modulates the neuron firing pattern dynamics.Science China Physics，Mechanics＆Astronomy，2013，42（2）：210～216（in Chinese））

10王海侠，陆启韶.对称电耦合连接方式下的多尺度同步行为和转迁过程.动力学与控制学报，2011，9（3）：214～218（Wang H X，Lu Q S.Multi-time-scale synchronization and transitions with symmetrical and electrical coupling schemes.Journal of Dynamics and Control，2011，9（3）：214～218（in Chinese））

11 Baer S M，Erneux T，Rinzel J.Slow passage through a Hopf bifurcation：Delay，memory effects，and resonance. SIAM Journal on Applied Mathematics，1989，49：55～71

DYNAM ICS ANALYSISOF SYNCHRONOUS BURSTING IN TWO-COMPARTMENT NEURON MODEL*

Meng Pan1†Lu Qishao2Zhao Yong3Dong Jianwei1
（1.School of Basic Courses，Guangdong Pharmaceutical University，Guangzhou 510006，China）（2.School ofAeronautical Science and Engineering，Beihang University，Beijing 100083，China）（3.School of Mathematics and Information Science，Henan Polytechnic University，Jiaozuo 454000，China）

A two-compartment neuronmodelwith outside current feedback is considered in order to study the dynamics of bursting patterns.Firstly，on the base of numerical simulation，the behavior of phase synchronization for the spikes in the soma and dendrite compartments is investigated.Secondly，by using fast-slow dynamics analysis，two-parameter bifurcation analysis of the fast subsystem is performed in the two-parameter plane.It is shown that three condimension-2 bifurcation points are generated in the fast subsystem，i.e.，fold-Hopf bifurcation ZH，cusp bifurcation CP and Bogdanov-Takens bifurcation BT.Finally，these condimension-2 bifurcation points determine that different bursting oscillations occurs in the system，such as“fold/fold”type，“Hopf/Hopf”type，“Hopf/homoclinic”type and“fold/homoclinic”type.Furthermore，the generation and transition mechanisms of different bursting patterns are discussed.The results offer significant data for understanding the important role of the geometric parameter in the variety of neuronal firing activities

bursting， synchronization， current-feedback， fast-slow analysis， bifurcation

10.6052/1672-6553-2016-023

2016-01-31收到第1稿，2016-03-26收到修改稿.

*国家自然科学基金资助项目（11402057，11502073，11272034，11371046）

†通讯作者E-mail：mengpan200e＠163.com

Received 31 January 2016，revised 26 March 2016.

*The project supported by the National Natural Science Foundation of China（11402057，11502073，11272024 and 11371046）

†Corresponding author E-mail：mengpan200e＠163.com