基于反距离权重法的长江流域参考作物蒸散量算法适用性评价

贾 悦，崔宁博，2※，魏新平，龚道枝，胡笑涛

（1.四川大学 水力学与山区河流开发保护国家重点实验室/水利水电学院，成都 610065；2.南方丘区节水农业研究四川省重点实验室，成都 610066；3.中国农业科学院农业环境与可持续发展研究所 作物高效用水与抗灾减损国家工程实验室，北京 100081；4.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

基于反距离权重法的长江流域参考作物蒸散量算法适用性评价

贾 悦1，崔宁博1，2※，魏新平1，龚道枝3，胡笑涛4

（1.四川大学 水力学与山区河流开发保护国家重点实验室/水利水电学院，成都 610065；2.南方丘区节水农业研究四川省重点实验室，成都 610066；3.中国农业科学院农业环境与可持续发展研究所 作物高效用水与抗灾减损国家工程实验室，北京 100081；4.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

为实现大区域尺度参考作物蒸散量（reference crop evapotranspiration，ET0）资料缺失情况下的准确计算，该文将长江流域划分为上、中、下游3个子区域，基于反距离权重法的新型空间展布方法得到3个虚拟站点分别代表每个子区域，利用长江流域102个站点1964-2013年近50a的逐日气象数据，根据FAO-56 Penman-Monteith（P-M）法、Hargreaves-Samani（HS）法、Irmark-Allen（I-A）法、Priestley-Taylor（P-T）法、Makkink（M-K）法、Penman-Van Bavel（PVB）法、1948年Penman（48-PM）法分别计算每个站点逐日ET0，并以P-M法为标准，利用Nash-Sutcliffe系数（CD）、逐日相对均方根误差（RMSE）、Kendall一致性系数（K）对其适用性进行评价，结果表明：在3个子区域6种ET0计算方法的日值与P-M法拟合方程确定系数R2均通过了极显著水平检验（α=0.01），长江上游P-T法ET0日值计算精度最高（ET0日值拟合方程斜率为1.030，RMSE=0.341 mm/d，CD=0.886，K=0.829），H-S法、I-A计算精度较低（ET0日值拟合方程斜率分别为1.427、1.308，RMSE=0.909、0.829 mm/d，CD= 0.581、0.523，K=0.792、0.742），长江中、下游PVB法计算精度最高，P-T法计算精度次之，H-S法与I-A法计算精度较低；长江上游6种算法ET0月值的计算精度由高到低依次为P-T法、PVB法、M-K法、48-PM法、H-S法、I-A法，与P-M法的平均误差分别为0.27、0.35、0.51、0.48、0.74、0.78 mm/d；长江中、下游6种算法计算精度由高到低为PVB法、P-T法、M-K法、48-PM法、H-S法、I-A法；整个长江流域P-T法、PVB法与P-M法ET0计算结果相对误差均在35%以下，H-S法、I-A法计算精度较低，其相对误差基本高于40%；因此，PVB法与P-T法在整个长江流域的计算精度较高，可作为长江流域ET0简化计算推荐方法。

气候变化；蒸散；模型；长江流域；参考作物蒸散量；反距离权重；空间展布；适用性评价

贾 悦，崔宁博，魏新平，龚道枝，胡笑涛.基于反距离权重法的长江流域参考作物蒸散量算法适用性评价[J].农业工程学报，2016，32（6）：130-138.doi：10.11975/j.issn.1002-6819.2016.06.018 http://www.tcsae.org

Jia Yue,Cui Ningbo,Wei Xinping,Gong Daozhi,Hu Xiaotao.Applicability evaluation of different algorithms for reference crop evapotranspiration in Yangtze River Basin based on inverse distance weighted method[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE）,2016,32(6):130－138.(in Chinese with English abstract) doi：10.11975/j. issn.1002-6819.2016.06.018 http://www.tcsae.org

0 引言

参考作物蒸散量（reference crop evapotranspiration，ET0）是一项重要的农业和水文变量，是确定作物需水量的重要因素之一，也是灌溉制度制定、流域规划、灌溉排水工程设计的重要依据[1]。目前，ET0计算方法有50多种，总体分为综合法、温度法、辐射法3大类[2]。1998年FAO-56分册推荐的FAO-56 Penman-Monteith（P-M）法因综合考虑各种气象因素的影响，具有严谨的理论依据、较高的计算精度[3-5]被广泛作为不同区域ET0计算的标准方法。但P-M法对气象资料的要求高，计算过程较复杂，在气象资料不完整区域难以使用，因此ET0简化算法研究成为国际气象学、水文学和农田水利学的研究热点，基于温度法的Hargreaves-Samani法[6]，基于辐射法的Priestley-Taylor法[7]，基于综合法中的Penman-Van Bavel法[8]等ET0简化算法相继被提出，但是这些方法易受自然地理、气候特点等因素影响，在不同区域其计算精度存在明显差异，因此，通过对已有简化算法的区域适应性评价找到适用于特定区域的ET0简化计算方法尤为重要。

针对不同地区ET0算法的适用性评价，国内外已有了部分研究。Azhar和Perera[9]分析了10种ET0算法在澳大利亚东南部的适用性，指出不同地区适用的方法不同，与实测数据相比，P-M法的误差在21%～29%之间，H-S法的误差在18%～31%之间；Tabari[10]分析了4种ET0算法在伊朗4种不同气候地区的适用性，指出Turc法在寒冷干旱地区、Hargreaves法在温暖潮湿与半干旱地区的计算精度均较好，总体上这2种算法计算精度高于Marrink法与Priestley-Taylor法；Xystrakis和Matzarakis[11]分析了13种ET0算法在希腊南部的克里特岛的适用性，指出Turc法和Hansen法计算精度最高；赵璐等[12]分析了Hargreaves法等4种ET0算法在川中丘陵区的适用性，指出Hargreaves校正法、Priestley-Taylor法与P-M法误差最小，可作为川中丘陵区ET0简化计算模型；李志[13]分析了6种ET0算法在黄土高原的适用性，指出Hargreaves法在黄土高原计算精度较高，Priestley-Taylor法则较低；袁小环等[14]分析了4种不同ET0算法在北京地区的适用性，以实测蒸散量值为标准，指出Penman-van Bavel法的精度最高，与实测蒸散量的一致性指数达到了0.9左右；胡庆芳等[15]在中国对Hargreaves法进行了校正，并对校正后公式的适用性进行了评价，指出校正后的Hargreaves法在西南、西北地区的计算精度明显提高。以上研究表明，受区域差异性影响，不同ET0简化算法的区域适用性存在明显差异。

反距离权重法是一种充分考虑各因素之间地域性联系的空间展布方法，因其原理简便，结果精确已被广泛应用在数据处理中，曾丽红等[16]在研究近60a东北地区ET0的变化时，采用反距离权重法对缺测或不合理数据进行插值填补，计算得到逐年ET0，指出其空间分布与相对湿度及温度的分布有关，其结论较为可靠；张山清和普宗朝[17]在研究新疆地区ET0时指出，反距离权重法的计算效果较好；高歌等[18]在研究日降水量的插值方法时指出，使用反距离权重法估算区域日降水量，其结果与实测值的相关系数达到了0.83，以上研究表明，使用反距离权重法解决空间展布问题具有一定的优越性。

目前，对较大区域尺度ET0简化算法适用性评价的研究较少，对长江流域的相关研究还未有报道，且现有研究在进行ET0计算时，多是直接选定代表站点或将各站点ET0简单平均，以代表整个流域的ET0，忽略了选择站点的代表性以及站点区位差异造成的影响。本文在已有研究的基础上，综合考虑站点海拔、经纬度的差异与联系，采用基于反距离权重法的新型空间展布方法，在长江流域对6种不同ET0简化算法的适用性进行评价，为长江流域ET0简化计算提供科学依据。

1 研究区域概况及数据来源

1.1 研究区域概况

长江是中国第一大河，全长约6 300 km，流域遍及贵州、甘肃、陕西、河南、广西、广东、浙江、福建8个省（自治区），面积达180万km2，约占中国陆地总面积20%。流域内地形地貌条件复杂，自西向东流域内有高原、山地、盆地、丘陵、平原和湖泊等差异显著的地貌特征，流域总落差达5 300 m[19]。长江流域降水量时空变异性较大，中下游降水大于上游，且年内分配极为不均，主要集中在4～10月。因长江流域面积较大，横跨范围较广，考虑地形条件对ET0计算结果影响，将长江流域按海拔、经度分区，海拔1 500 m以上地区分为长江上游，海拔200～1 500m地区分为长江中游，海拔低于200 m地区分为长江下游，结合资料系列的完整性本文选取流域代表性站点102个，流域分区及站点分布情况见图1。

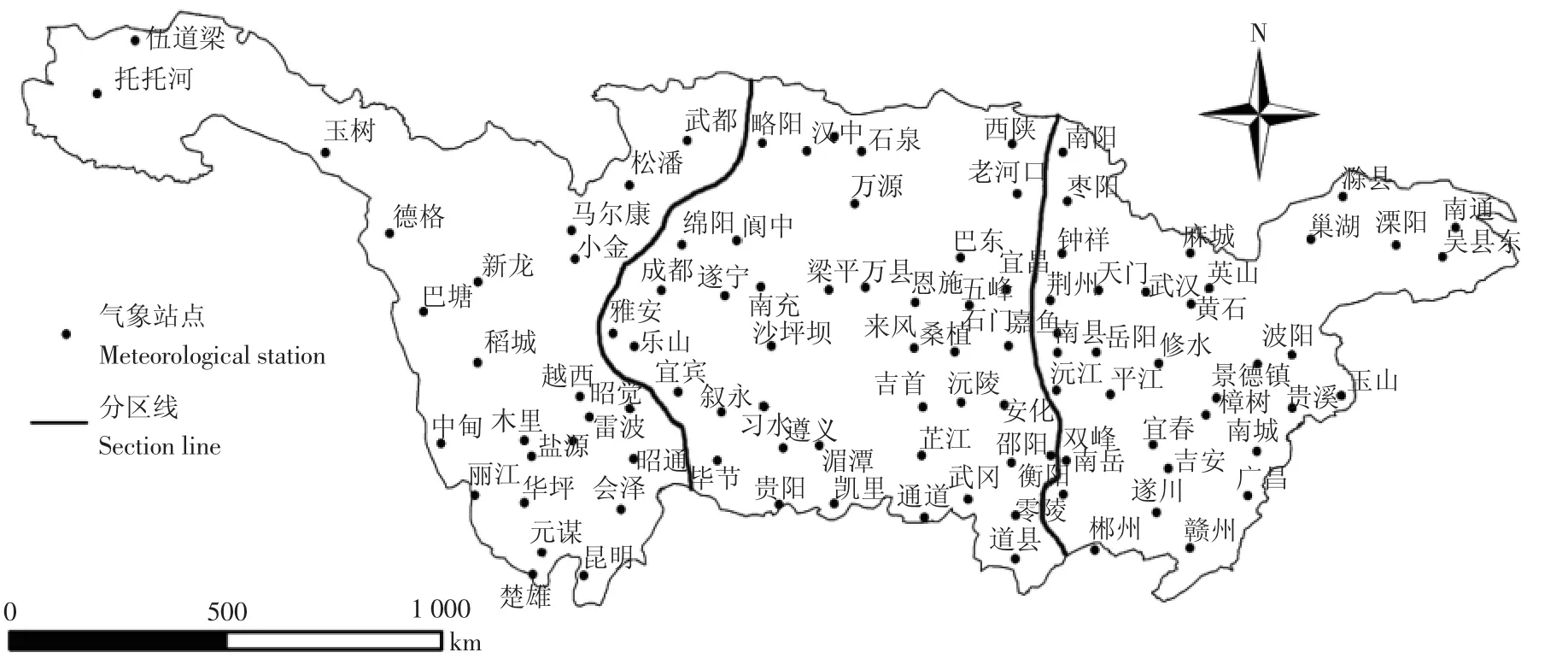
图1 长江流域分区及站点分布图Fig.1 Area division and stations distribution in Yangtze River Basin

1.2 数据来源

本文气象资料来自国家气象信息中心，数据经过严格控制，质量良好。本文选取长江流域102个气象站点（图1）1964～2013年逐日的气象资料，对部分站点缺测数据（占全部数据的0.48%），采用线性内插法补全，得到逐日最高气温（Tmax）、最低气温（Tmin）、平均气温（Tmean）、日照时数（n）、距地面2 m高处的风速（计算时采用FAO推荐方法[4]由10 m风速换算得出风速U2）和相对湿度（RH）。

2 研究方法

2.1 反距离权重法

反距离权重法IDW（inverse distance weighted）是根据地理学的第一定律，即距离越接近的2个事物具有越相近的属性，反之这种相似性随着距离的增大而减小[20-21]，认为与插值点距离最近的样本点对插值点值的贡献最大，其贡献与距离成反比，通过计算以插值点为圆心，以R为半径的圆内样本点的加权平均值来确定插值[22]。其公式表示如下：

式中Z为估计值；Zi为第i（i=1，…，n）个样本值di是距离，n为用于插值的气象站点的数量；p是距离的幂，它的选择标准是最小平均绝对误差，默认p=2。

2.2 空间展布方法

由于长江流域范围较大，流域内地形地貌条件复杂，不同站点海拔差异明显，所以，直接将流域内站点ET0数值做平均或选择代表站点来代表整区域ET0具有明显的局限性。因此，本文综合考虑各站点海拔、经度、纬度差异对ET0计算结果的影响，采用基于反距离权重法的新型空间展布方法，最大限度地消除地域差异，以增强选择站点的代表性。

为增强选择站点的代表性，本文将长江流域上、中、下游3个子流域各站点经度、纬度、海拔做平均，得到3个虚拟站点，根据反距离权重法计算各子流域对应虚拟站点的权重，将每个站点各气象因子乘以权重后相加，从而得到3个虚拟站点1964—2013年逐日气象资料，再计算3个虚拟站点ET0数值，以代表整个流域值。权重计算公式如下：

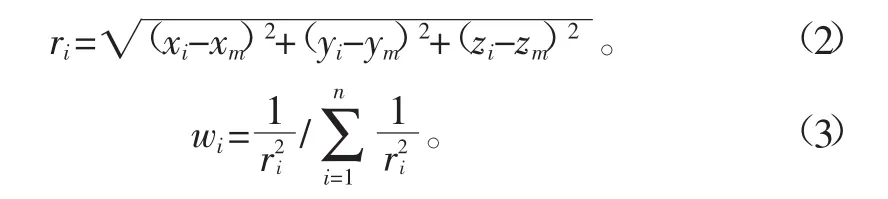
式中xi、yi和zi分别表示所求站点的经度（°）、纬度（°）和海拔（m）；xm、ym、zm分别表示所求虚拟站点的经度、纬度、海拔；ri为第i个站点到虚拟站点的距离；n为流域站点个数；wi为第i个站点的权重。

例如成都、乐山、南充3个站点，其经度、纬度、海拔分别为成都（104.01°E，30.40°N，506.10 m）、乐山（103.45°E，29.34°N，424.20 m）、南充（106.06°E，30.47°N，309.7 m），基于3个站点得到的虚拟站点坐标为（104.51°E，30.07°N，413.33 m），按公式（2）、（3），计算得3个站点的权重分别为0.318、0.339、0.343，将3个站点的气象因子乘以权重后相加，得到虚拟站点的气象因子值。

2.3 参考作物蒸散量计算方法

2.3.1 FAO56 Penman-Monteith法

1998年FAO-56分册推荐的FAO-56Penman-Monteith（P-M）方法以能量平衡和空气动力学原理为基础，具有较完备的理论依据和较高的计算精度，在世界范围内得到广泛使用。以P-M法计算结果作为标准值，公式如下[4]：

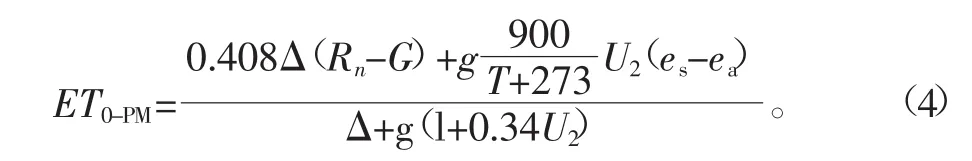
式中ET0-PM是由P-M法计算得到的ET0值，mm/d；Rn是净辐射量，MJ/m2.d；T是2 m高处的日均气温，℃；G是土壤热量通量密度，MJ/m2.d；U2是2 m高处的风速，m/s；es是饱和水汽压差，kPa；ea是实际水汽压差，kPa；Δ是蒸汽压曲线的斜率，kPa/℃；γ是干湿计常数，kPa/℃。

2.3.2 Hargreaves-Samani法

20世纪50年代Hargreaves和Samani共同提出基于温度和辐射计算ET0的方法Hargreaves-Samani（H-S）法，因对数据资料要求较低，计算精度较高，应用较广泛，公式如下[6]：

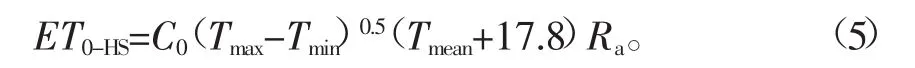
式中ET0-HS是H-S法计算得到的ET0，mm/d；Tmax、Tmin、Tmean分别代表日最高、最低和平均温度，℃；Ra为大气顶层辐射，MJ/m2.d；C0为转换系数，取0.000 936。

2.3.3 Irmark-Allen法

Irmark-Allen法（I-A法）是由Irmark等在2003年提出的基于温度与净辐射计算ET0的方法，其在湿润环境下计算精度较高，且计算结果要优于其他温度、辐射法，公式如下[23]：

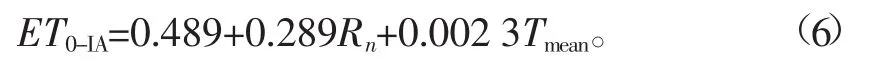
式中ET0-IA为由I-A法计算得到的ET0，mm/d；Tmean为平均温度，℃；Rn为作物表面的净辐射，MJ/m2.d。

2.3.4 Priestley-Taylor法

1972年Priestley-Taylor基于平衡蒸发，利用湿润路面的资料提出Priestley-Taylor（P-T）法，该方法在湿润地区的计算精度较高，公式如下[7]：

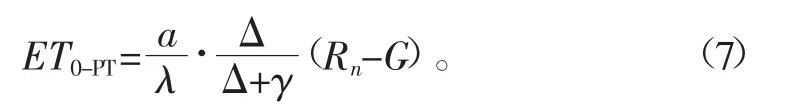
式中ET0-PT为由P-T法计算得到的ET0，mm/d；λ为水汽化潜热，取2.45 MJ/kg；其余参数与P-M公式各参数一致。

2.3.5 Marrink法

1957年Marrink基于太阳辐射提出Marrink（M-K）法，该方法计算简便，在寒冷地区的适用性已得到了验证，具体公式如下[24]：

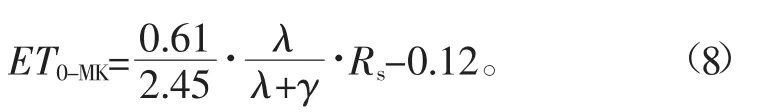
式中ET0-MK为由M-K法计算得到的ET0，mm/d；Rs为太阳辐射，MJ/m2.d；其余参数与P-M法各参数一致。

2.3.6 1948 Penman法

1948年，Penman提出了无水汽水平输送条件下计算ET0的方法（48-PM法），其具体公式如下[25]：

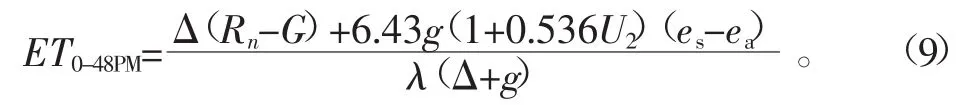
式中ET0-48PM是由48-PM法计算得到的ET0，mm/d；其余参数与P-M法参数一致。

2.3.7 Penman-Van bavel法

1966年Cornelius Van Bavel修正了Penman法中的经验参数，提出了Penman-Van bavel（PVB）法，该方法在计算日尺度的ET0是精度较高，其具体公式如下[8]：

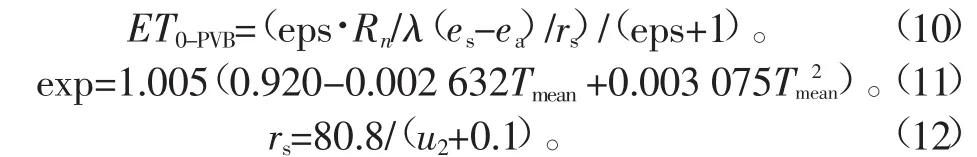
式中ET0-PVB是由PVB法计算得到的ET0，mm/d；Tmean为平均温度，℃；其余参数与P-M法一致。

2.4 评价方法

本文采用Nash-Sutcliffe系数（CD）、逐日相对均方根误差（RMSE）和Kendall一致性系数（K）来评价各计算方法与标准方法计算结果的精度及一致性，其中，CD与K的值越大、RMSE的值越小，该算法与P-M法的一致性越好、计算精度越高，具体公式如下：

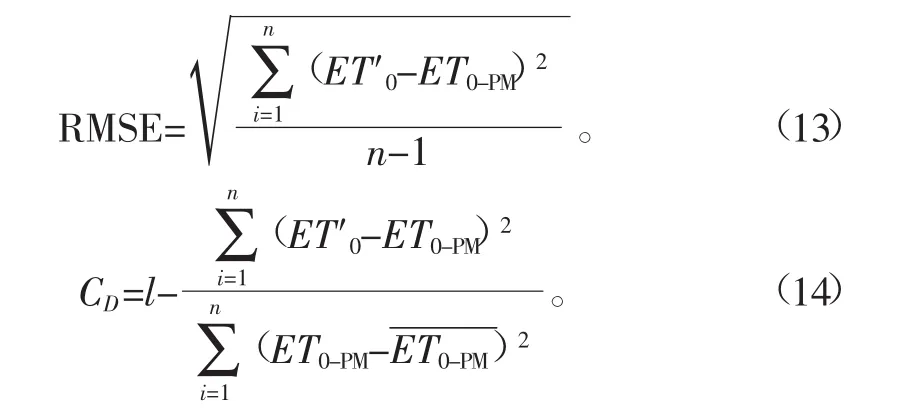
式中n为样本数量；ET0′为待检验方法计算的ET0值，mm/d； ET0-PM为标准P-M法计算的ET0值，mm/d；为标准PM法计算的ET0均值，mm/d；C为待检验方法与标准P-M法计算结果中拥有一致性元素的对数；D为待检验方法与标准P-M法计算结果中不具有一致性元素的对数（对于2个元素（Xi，Y）i、（Xj，Y）j，若出现Xi＞Xj且Yi＞Yj，或者是Xi＜Xj且Yi＜Yj2种情况，则称这2个元素是一致的）。

3 结果与分析

3.1 长江流域不同ET0简化算法日值适用性评价

长江流域不同ET0简化算法与P-M法日值（ET0-PM）的拟合方程及确定系数如表1显示。表1显示，与ET0-PM相比，在长江上游ET0-HS、ET0-IA、ET0-PT、ET0-48PM均有不同程度偏大，与ET0-PM拟合方程的斜率分别为1.427、1.308、1.030、1.143，ET0-MK与ET0-PVB则偏小，与ET0-PM拟合方程的斜率分别为0.857、0.946，即ET0-PT与ET0-PVB的斜率更接近1；在长江中游ET0-MK、ET0-PVB与ET0-PM拟合方程斜率更接近于1，分别达到了0.936、1.065；在长江下游ET0-PVB与ET0-PM拟合方程的斜率最接近于1，斜率为1.005；在整个长江流域，ET0-MK、ET0-PVB拟合方程斜率更接近于1，分别为0.891、1.054。不同方法在整个流域拟合方程的确定系数R2均在0.85以上，且均达到了极显著水平（α=0.01），P-T法、M-K法、48-PM法与PVB法在长江流域的计算精度明显高于H-S法与I-A法，且P-T法、M-K法、PVB法分别在长江上、中、下游的计算精度较高，且PVB法在整个流域计算精度均较高。

表1 长江流域不同ET0简化算法与P-M法日值拟合方程及确定系数Table 1 Imitative equation and determination coefficient between different daily ET0simplification calculation and P-M in Yangtze River Basin

3.2 长江流域不同ET0日值简化算法精度对比

表2为长江流域不同区域不同ET0简化算法精度对比，表2显示，长江流域上游ET0-PT精度最高，RMSE值最低（仅为0.341），CD与K的值最高，分别为0.886、0.829；ET0-MK、ET0-PVB精度次之，RMSE值分别为0.361、0.419，CD与K的值均在0.759以上，因此其计算结果与ET0-PM一致性较高；ET0-HS和ET0-IA精度较低，RMSE较高，分别达到了0.909与0.829，CD与K值较低，CD值仅为0.581、0.523，K值仅为0.792、0.742；长江流域中、下游ET0-PVB精度最高，RMSE值分别为0.201、0.306，CD值分别达到了0.973、0.954，K值分别达到了0.926、0.869，计算精度明显高于其他方法，ET0-PT、ET0-MK、ET0-48PM精度次之，ET0-HS与ET0-IA精度较低，RMSE的值均在 1.095以上，且CD的值均在0.587以下；整个长江流域ET0-PVB精度最高，RMSE、CD、K的值分别为 0.166、0.976、0.908，ET0-PT、ET0MK法、ET0-48PM精度次之，ET0-HS和 ET0-IA精度较低。综上所述，H-S法、I-A法在流域内不同区域的计算精度均较低，其RMSE值均在0.829以上，PVB与P-T法在整个流域的计算精度均较高，其RMSE值均在0.477以下，CD与K值均在0.821以上，因此，P-T法与PVB法在长江流域的计算精度最高，可作为长江流域ET0简化计算推荐方法。

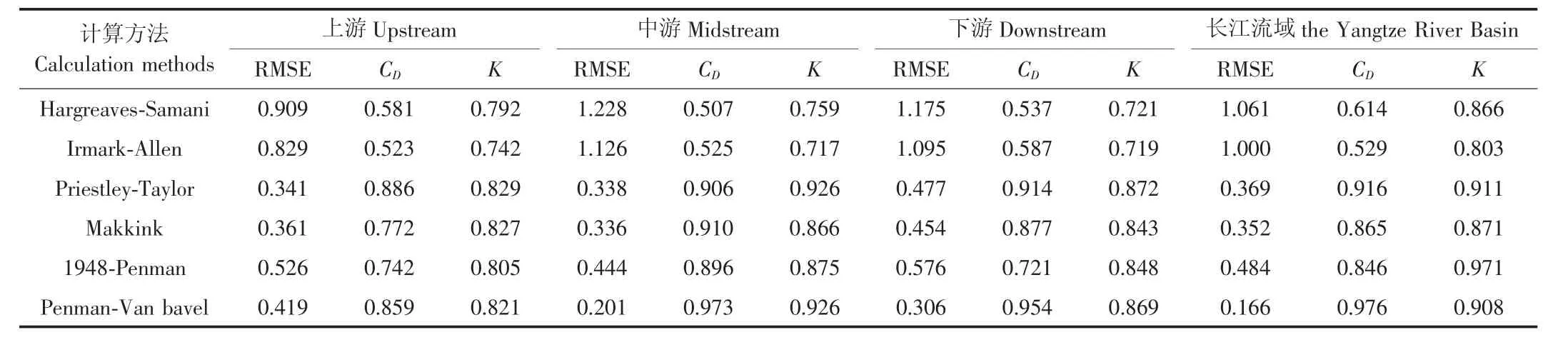
表2 长江流域不同区域ET0简化算法精度对比Fig.2 Comparison ET0accuracy among simplification calculation in different area in Yangtze River Basin

3.3 长江流域不同ET0简化算法月值适用性评价

长江流域不同区域各简化算法参考作物蒸散量月值如图2显示。图2显示，不同ET0简化计算方法得到的ET0月值在年内变化趋势基本一致，总体呈先增加后减少的二次抛物线形式，这与杜加强等[26]在黄河上游的研究成果一致。图2a显示，与ET0-PM相比，在长江上游ET0-PT、ET0-PVB精度较高，ET0-48PM与ET0-MK精度次之，ET0-HS和ET0-IA精度较低，平均绝对误差分别为0.27、0.35、0.51、0.48、0.74和0.78mm/d；图2b显示，与ET0-PM相比，在长江中游ET0-PVB与ET0-PT精度较高，ET0-48PM与ET0-MK的精度次之，ET0-HS和ET0-IA精度较低，平均绝对误差分别为0.13、0.34、0.40、0.46、1.07、1.11 mm/d；图2c显示，在长江下游，与ET0-PM相比，ET0-PVB、ET0-PT精度较高，ET0-48PM与ET0-MK精度次之，ET0-HS和ET0-IA精度较低，平均绝对误差分别为0.12、0.30、0.47、0.48、0.98、1.04 mm/d；图4d显示，在整个长江流域ET0-PVB、ET0-PT精度较高，ET0-HS和ET0-IA精度较低。因此，对于长江流域PVB法与P-T法在计算ET0月值的精度较高，且计算过程较简便，可作为长江流域ET0月值计算的简化模型。

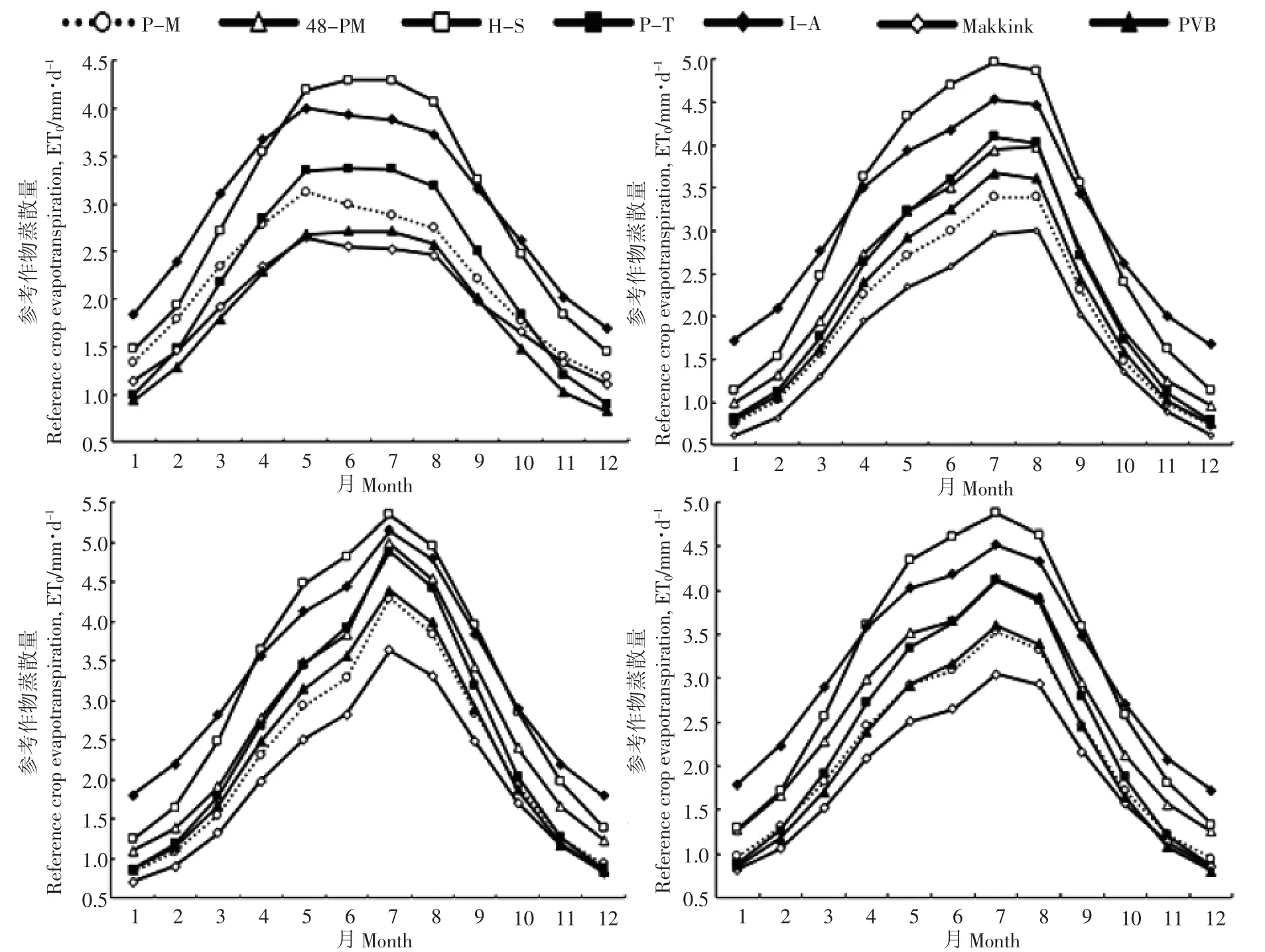
图2 长江流域不同区域不同简化算法参考作物蒸散量月值对比Fig.2 Monthily ET0comparison among different simplification calculation in different area in Yangtze River Basin

3.4 长江流域ET0计算方法适用性的空间差异

长江流域不同ET0简化算法与P-M法相对误差的空间分布如图3所示。图3a显示，与ET0-PM相比，ET0-HS在长江流域上游、下游的相对误差分布在25%～40%，在长江中游ET0-HS的相对误差较大，基本在40%以上，即ET0-HS在长江流域上、下游的精度要高于中游；图3b显示，与ET0-PM相比，ET0-IA在长江流域上游的精度较高，相对误差在25%～55%，中下游精度较低，相对误差在55%～85%，即ET0-IA在长江流域的精度较低；图3c显示，ET0-PT精度明显高于ET0-HS与ET0-IA，整个流域ET0-PM相对误差均在10%～40%；图3d显示，与ET0-PM相比，ET0-MK在长江流域的相对误差总体较小，最大仅为36%，绝大多数区域相对误差在10%～30%；图3e显示，与ET0-PM相比，ET0-48PM在中游的精度较高，相对误差多集中在10%～25%之间，其余区域相对误差也在40%以下；图3f显示，与ET0-PM相比，ET0-PVB精度最高，相对误差基本在30%以下。综上所述，P-T法、PVB法在长江流域计算的相对误差要低于H-S法与I-A法，48-PM法则仅在长江中游的计算精度较高，因此，P-T法和PVB法可作为长江流域ET0简化计算的推荐模型，同时所有方法均在南岳站出现异常，这可能与南岳站海拔远高于周围其他站点有关。

对于致密型腺体良恶性的判断，DBT准确性（85.2%）较FFDM（72.9%）高，比较差异显著（P＜0.05）。见表2。

4 讨论

目前，对大区域ET0计算方法适用性评价的研究较少，且针对大区域尺度ET0计算的空间展布问题，仍未找到合适的方法以得到最具有代表性的站点表征整个流域的ET0。胡庆芳等[13]在全国范围内对Hargreaves法进行了校正，将全国分为7个流域，对每个站点的Hargreaves法均进行了校正，然后在不同流域进行简单平均，并在7个流域选择7个站点对得到的Hargreaves校正公式适用性进行了评价，但站点代表性无法得到验证。刘战东等[27]在黄淮海地区研究ET0计算方法的适用性时，选择了7个站点以代表整个流域，指出Hargreaves法在该地区计算精度最高，但也未论证选择站点是否具有代表性。本文提出基于反距离权重法的新型空间展布方法，计算每个站点的权重，将每个站点的气象资料乘以权重后相加，得到虚拟站点，以代表整个流域的气象因子用以表征ET0。由于反距离权重法考虑了地理学第一规律，距离越近，两个事物属性越相似，曾丽红等[16]在研究近60a东北地区ET0的变化时，采用反距离权重法对缺测或不合理数据进行插值填补，计算得到逐年ET0，指出其空间分布与相对湿度及温度的分布有关，其结论较为可靠；张山清和普宗朝[17]在研究新疆地区ET0时指出，反距离权重法的计算效果较好，因此，本文采用基于反距离权重法的新型空间展布方法，充分考虑流域内各站点经度、纬度以及海拔差异对计算结果的影响，得到的站点较直接选择代表站或简单平均，其代表性将会显著提高。

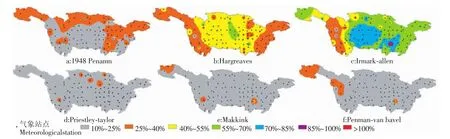
图3 长江流域不同ET0算法与P-M法相对误差的空间分布Fig.3 Space distribution of relative error between different ET0calculation and P-M in Yangtze River Basin

本研究表明，长江流域P-T法与PVB法的计算精度较高，H-S法与I-A法计算精度较低，丁斌等[28]在研究长江流域温度的时空变化时，发现1960-1980年长江流域气温呈波动下降，1980年后出现回升，与其它流域气温变化趋势不同，曾小凡等[29]也同样发现了长江流域气温变化的特异性，同时由于流域面积较大，流域内地形地貌条件复杂，流域海拔总落差达到5 300 m[30]，气温垂直分布明显，昼夜温差大，对温度法（尤其是H-S法中的Tmax-Tmin项）计算结果影响较大，且H-S模型易受温度、风速和云层厚度等气候变化的影响，在日尺度上浮动、变化较大，适用于5 d及更大时间尺度的ET0计算[19]，以上可能是导致温度法在长江流域计算精度偏低的原因；PVB法考虑了风速、温度、湿度以及太阳辐射的影响，综合考虑了辐射项和空气动力学项的影响，计算精度较高，但对气象资料要求严格，对资料缺乏地区的适用性受到限制。Caporusso和Rolim[31]在巴西的圣保罗地区对P-T法的适用性研究时指出，P-T法在气候潮湿炎热时的计算精度最高，长江流域为亚热带季风气候，其气候条件潮湿炎热，因此P-T法虽只考虑了太阳辐射的影响，但在整个流域的计算精度较高，且对数据资料的要求较低，因此可作为长江流域ET0简化计算的推荐模型。

本研究发现，6种方法在南岳站附近的ET0计算精度均出现了显著降低，P-T法、PVB法在除南岳站之外的整个流域，其计算精度均较高，南岳站海拔为1 266 m，而周围其他站点的海拔仅为100 m左右，南岳站海拔远高于周围其他站点，陈涛等[32]在研究南岳高海拔地区与周围低海拔地区气温变化特征对比时指出，由于南岳站海拔较高，受人为因素对环境的影响较小，因此与周围地区气候环境存在的较大差异可能是导致南岳站气象条件出现异常，影响ET0计算的重要原因。

5 结论

本文基于长江流域102个代表站点1964-2013年逐日气象资料，采用基于反距离权重法的新型空间展布方法，得到虚拟站点以代表长江流域上、中、下游3个子流域的气象因子，分别通过6种不同算法计算了每个站点的ET0，并以P-M法计算结果为标准，对其适用性进行了评价，结果表明：

1）ET0日值计算精度PVB法、P-T法计算精度较高，M-K法、48-PM法次之，H-S法、I-A法计算精度较低。6种不同方法计算的ET0与P-M法结果拟合方程的相关性均达到了极显著水平（α=0.01），长江上游P-T法计算精度最高（拟合方程斜率为1.030，RMSE=0.341，CD=0.886，K= 0.829），PVB法计算精度次之（拟合方程斜率为0.946，RMSE=0.419，CD=0.859，K=0.821），H-S法与I-A法计算精度较低（拟合方程斜率分别为1.427、1.308，RMSE=0.909、0.829，CD=0.581、0.523，K=0.792、0.742）；长江中、下游PVB法计算精度最高，P-T法计算精度次之，H-S法与I-A法计算精度较低。

2）长江上游6种算法ET0月值的计算精度由高到低依次为P-T法、PVB法、M-K法、48-PM法、H-S法、I-A法，与P-M法的平均误差分别为0.27、0.35、0.51、0.48、0.74、0.78 mm/d；长江中（下）游6种算法计算精度由高到低为PVB法、P-T法、M-K法、48-PM法、H-S法、I-A法，与P-M法的平均误差分别为0.13 mm/d（0.12 mm/d）、0.34（0.30）、0.40（0.47）、0.46（0.48）、1.07（0.98）、1.11（1.04）。

3）整个流域内，辐射法与综合法的计算精度较高于温度法，其中PVB法在整个流域内的相对误差基本在30%以下，P-T法相对误差基本集中在14%～35%之间，H-S法与I-A法的相对误差基本在40%以上，因此，P-T法与PVB法在长江流域的计算精度较高，可作为长江流域ET0计算的推荐模型。

4）本文通过基于反距离权重法的新型空间展布方法，综合考虑站点之间经度、纬度和海拔之间的关系，得到新的站点以代表整个流域，这种方法的正确性有待进一步在其他流域进行验证；由于不同计算方法在南岳站的计算精度均较低，因此，针对南岳站气候变化差异性的影响，来确定适合南岳站ET0计算的标准模型还有待进一步研究。

[1]康绍忠.农业水土工程概论[M].北京：中国农业出版社，2005.

[2]徐俊增，彭世彰，丁加丽，等.基于蒸渗仪实测数据的日参考作物蒸发腾发量计算方法评价 [J].水利学报，2010，41(12)：1497-1505. Xu Junzeng,Peng Shizhang,Ding Jiali,et al.Evaluation of methods for estimating daily reference crop evapotranspiration based on lysimeter grass experiments[J].Journal of Hydraulic Engineering,2010,41(12):1497-1505.(in Chinese with English abstract)

[3]Allen R G,Pereira L S,Raes D,et al.Crop evapotranspirationguidelines for computing crop water requirements[M].Rome: Food and Agriculture Organization of United Nation,1998.

[4]王声锋，汪顺生，段爱旺，等.豫西北几种ET0计算方法的比较及Hargeaves公式的修正[J].灌溉排水学报，2010，29（6）：29-33. Wang Shengfeng,Wang Shunsheng,Duan Aiwang,et al. Evaluation on several methods for estimating ET0 and modified hargeaves formulas[J].Journal of Irrigation and Drainage,2010, 29(6):29-33.(in Chinese with English abstract)

[5]孙庆宇，佟玲，张宝忠，等.参考作物蒸发蒸腾量计算方法在海河流域的适用性[J].农业工程学报，2010，6(11)：68-72. Sun Qingyu,Tong Ling,Zhang Baozhong,et al.Comparison of methods for calculating reference crop evapotranspiration in Haihe River basin of China[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2010,26(11):68－72.(in Chinese with English abstract)

[6]Hargreaves G H,Allen R G.History and evaluation of Hargreaves evapotranspiration equation[J].Jounal of Irrigation and Drainage Engineering,2003,129(1):53-63.

[7]Priestley C H B,Taylor R J.On the assessment of surface heat flux and evapotranspiration using large-scale parameters[J]. Monthly Weather Review,1972,100(2):81-92.

[8]Van Bavel C H M.Potential evapotranspiration:the combination concept and its experimental verification[J].Water Resources Research,1966,2(3):23-34.

[9]AzharA H,Perera B JC.Evaluation ofreference evapotranspiration estimation methods under Southeast Australian conditions[J].Journal of Irrigation and Drainage Engineering,2010,137(5):268-279.

[10]Tabari H.Evaluation of reference crop evapotranspiration equations in various climates[J].Water resources management, 2010,24(10):2311-2337.

[11]Xystrakis F,Matzarakis A.Evaluation of 13 empirical reference potential evapotranspiration equations on the island of Crete in southern Greece[J].Journal of Irrigation and Drainage Engineering, 2010,137(4):211-222.

[12]赵璐，梁川，崔宁博，等.不同ET0计算方法在川中丘陵区的比较及改进[J].农业工程学报，2012，28(24)：92-98. Zhao Lu,Liang Chuan,Cui Ningbo,et al.Comparison and improvement of different calculation methods for ET0 in hillyarea of central Sichuan Basin[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2012,28(24):92－98.(in Chinese with English abstract)

[13]李志.参考作物蒸散简易估算方法在黄土高原的适用性[J].农业工程学报，2012，28（6）：106-111. Li Zhi.Applicability of simple estimating method for reference crop evapotranspiration in Loess Plateau[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2012,28(6):106-111.(in Chinese with English abstract)

[14]袁小环，杨学军，陈超，等.基于蒸渗仪实测的参考作物蒸散发模型北京地区适用性评价[J].农业工程学报，2014，30(13)：104-110. Yuan Xiaohuan,Yang Xuejun,Chen Chao,et al.Application assessment of reference evapotranspiration models in Beijing based on lysimeter measurement[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2014,30(13):104-110.(in Chinese with English abstract)

[15]胡庆芳，杨大文，王银堂，等.Hargreaves公式的全局校正及适用性评价[J].水科学进展，2011，22(2)：160-167. Hu Qingfang,Yang Dawen,Wang Yintang,et al.Global calibration of Hargreaves equation and its applicability in China [J].Advances In Water Science,2011,22(2):160-167.(in Chinese with English abstract)

[16]曾丽红，宋开山，张柏，等.近60年东北地区参考作物蒸散量时空变化[J].水科学进展，2010，21（2）：194-200. Zeng Lihong,Song Kaishan,Zhang Bai,et al.Spatiotemporal variability of reference evapotranspiration over the Northeast region of China in the last 60 Years[J].Advances In Water Science,2010,21(2):194-200.(in Chinese with English abstract)

[17]张山清，普宗朝.新疆参考作物蒸散量时空变化分析[J].农业工程学报，2011，27（5）：73-79. Zhang Shanqing,Pu Zongchao.Temporal and spatial variation characteristics of reference evapotranspiration in Xinjiang[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2011,27(5):73－79.(in Chinese with English abstract)

[18]高歌，龚乐冰，赵珊珊，等.日降水量空间插值方法研究[J].应用气象学报，2007，18(5)：732-736. Gao Ge,Gong Lebing,Zhao Shanshan,et al.Spatial interpolation methods of daily precipitation[J].Journal of Applied Meteorological Science,2007,18(5):732-736.(in Chinese with English abstract)

[19]许继军.分布式水文模型在长江流域的应用研究[D].北京：清华大学,2007. Xu Jijun.Application of a Distributed Hydrological Model to theYangtze River Basin[D].Beijing:Tsinghua University,2007.(in Chinese with English abstract)

[20]陈冬花，邹陈，王苏颖，等.基于DEM的伊犁河谷气温空间插值研究[J].光谱学与光谱分析，2011，31（7）：1925-1929. Chen Donghua,Zou Chen,Wang Suying,et al.Study on spatial interpolation of the average temperature in the Yili River Valley Based on DEM [J].Spectroscopy and Spectral Analysis, 2011,31(7):1925-1929.(in Chinese with English abstract)

[21]林忠辉，莫兴国，李宏轩，等.中国陆地区域气象要素的空间插值[J].地理学报，57（1）：47-56. Lin Zhonghui,Mo Xingguo,Li Hongxuan,et al.Comparison of three spatial interpolation methods for climate variables in China [J].Acta Geographica Sinica,2002,57(1):47-56.

[22]汤博，佟玲，康绍忠，等.站点密度及插值方法对ET0空间插值精度的影响[J].农业工程学报，29(13)：60-66. Tang Bo,Tong Ling,Kang Shaozhong.Effects of spatial station density and interpolation methods on accuracy ofreference crop evapotranspiration[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of theCSAE),2013,29 (13):60－66.(in Chinese with English abstract)

[23]Irmak S,Irmak A,Allen R G,et al.Solar and net radiation-based equations to estimate reference evapotranspiration in humid climate[J].Journal of Irrigation and Drainage Engineering,Asce, 2003,129(5):336-347.

[24]Makkink G F.Testing the Penman Formula by means of lysimeters[J].Instit.Water Engineers,1957,11:277-288.

[25]Penman H L.Natural evaporation from open water,bare soil and grass[C]//Proceedings of the Royal Society of London A: Mathematical,Physical and Engineering Sciences.The Royal Society,1948,193(1032):120-145.

[26]杜加强，舒俭民，刘成程，等.黄河上游参考作物蒸散量变化特征及其对气候变化的响应 [J].农业工程学报，2012，28（12）：92-100. Du Jiaqiang,Shu Jianmin,Liu Chengcheng,et al.Variation characteristics of reference crop evapotranspiration and its responses to climate change in upstream areas of Yellow River basin [J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2012,28 (12):92－100.(in Chinese with English abstract)

[27]刘战东，刘祖贵，秦安振，等.黄淮海地区基于温度的ET0计算方法比较及改进[J].节水灌溉，2014，4：1-7. Liu Zhandong,Liu Zugui,Qin Anzhen,et al.Comparison and Revision of ET0 Temperature-based Calculation Methods for Huanghuaihai Areas[J].Water Saving Irrigation,2014(4):1-6. (in Chinese with English abstract)

[28]丁斌，顾显跃，缪启龙.长江流域近50年来的气温变化特征[J].长江流域资源与环境，2006，15（4）：531-536. Ding Bin,Gu Xianyue,Miao Qilong.Characeristics in the variation of temperature over the Yangtze river valley over last 50 years[J].Resources and Environment in the Yangtze Basin, 2006,15(4):531-536.(in Chinese with English abstract)

[29]曾小凡，翟建青，苏布达，等.长江流域年平均气温的时空变化特征[J].长江流域资源与环境，2009，18（5）：427-431. Zeng Xiaofan,Zhai Jianqing,Su Buda,et al.Analysis of spatial and temporal characteristics of annual temperature in the Yangtzeriverbasin[J].Resources and Environment in the Yangtze Basin,2009,18(5):427-431.(in Chinese with English abstract)

[30]Peter D,Richard G A.Estmating reference evapotranspiration under inaccuratedataconditions[J].IrrigationandDrainageSystems,2002, 2(16):33-45.

[31]Caporusso N B,Rolim G S.Reference evapotranspiration models using different time scales in the Jaboticabal region of Sao Paulo, Brazil[J].Acta Scientiarum,2015,37(1):1-9.

[32]陈涛，叶成志，陈德桥，等.近58年南岳高山气温变化特征及与低海拔地区对比[J].气象科技，2013，41（4）：713-717. Chen Tao,Ye Chengzhi,Chen Deqiao,et al.Temperature variation contrast between Nanyue Mountain and low-elevation areas in past 58 years[J].Meteorologocal Science and Technology, 2013,41(4):713-717.(in Chinese with English abstract)

Applicability evaluation of different algorithms for reference crop evapotranspiration in Yangtze River Basin based on inverse distance weighted method

Jia Yue1,Cui Ningbo1，2※,Wei Xinping1,Gong Daozhi3,Hu Xiaotao4
(1.State Key Laboratory of Hydraulics and Mountain River Engineering&College of Water Resource and Hydropower,Sichuan University, Chengdu 610065,China;2.Provincial Key Laboratory of Water-Saving Agriculture in Hill Areas of Southern China,Chengdu 610066,China; 3.State Engineering Laboratory for Efficient Water Use and Disaster Loss Reduction of Crops,Institute of Environment and Sustainable Development in Agriculture,Chinese Academy of Agriculture Science,Beijing 100081,China;4.Key Laboratory of Agricultural Soil and Water Engineering in Arid and Semiarid Areas,Ministry of Education,Northwest A&F University/Institute of Water-saving Agriculture in Arid Areas of China,Yangling 712100,China)

In order to making true the exact calculation of reference crop evapotranspiration(ET0)and increase the accuracy with the lack of meteorological data in the large area,the Yangtze River Basin is divided into upstream,midstream anddownstream according to the altitude of the stations.A new method of space distribution based on Inverse Distance Weighted Interpolation method is raised which can present every substream,including upstream,midstream and downstream.This method can include the connection of different stations.There are 102 meteorological stations which can provide 50 years of daily meteorological data from 1963 to 2013.In this research,we used the methods of Penman-Monteith (P-M),Hargreaves-Samani(H-S),Irmark-ALLEN(I-A),Pristley-Taylor(P-T),Makkink(M-K),Penman-Van Bavel(PVB),1948 Penman(48-PM)to calculate daily ET0of every stations of the Yangtze River Basin.The method of Penman-Monteith can be used to be the standard method to calculate standard daily ET0to evaluate other methods because of its accuracy.The coefficient of Nash-Sutcliffe,the daily relative root mean square error,the consistency coefficient of Kendall can be used to evaluate the precision index of the method.The result showed that the best method of daily ET0imitative effect compared with P-M is PVB in the three substreams,because the slope of the imitative equation of PVB in upstream is 0.946,the slope in midstream is 1.065,and the slope in downstream is 1.005.The method of Pristley-Taylor has a better effect in the midstream and downstream,and the slopes of the imitative equation are 1.030 and 1.201.The method of Makkink also has a good effect in the midstream and downstream,and the slopes are 0.857 and 0.936.The determination coefficient of daily ET0imitative equation of these six methods all achieved very significant levels(α=0.01)in three substreams.The methods of Pristley-Taylor and Penman-Van Bavel have high calculation accuracy in all area of the Yangtze River Basin,and the highest absolute error of monthly ET0is 0.55 mm/d using the method of Pristley-Taylor,at the same time the highest absolute error of monthly ET0is 0.48 mm/d using the method of Penman-Van Bavel.The effect of the methods of Hargreaves-Samani and Irmark-ALLEN are worse than other methods to calculate monthly ET0in the whole Yangtze River Basin.The method of Pristley-Taylor is the best method to calculate ET0in the upstream of the Yangtze River Basin, because the daily relative root mean square error is 0.341 mm/d,the coefficient of Nash-Sutcliffe is 0.886,and the consistency coefficient of Kendall is 0.829.The method of Penman-Van Bavel is the best method to calculate ET0in the midstream and downstream of the Yangtze River Basin.In the midstream,the daily relative root mean square error is 0.201 mm/d,the coefficient of Nash-Sutcliffe is 0.973,and the coefficient of Nash-Sutcliffe is 0.926.In the downstream,the daily relative root mean square error is 0.306 mm/d,the coefficient of Nash-Sutcliffe is 0.954,and the consistency coefficient of Kendall is 0.869.In the Yangtze River Basin,the relative error of Pristley-Taylor and Penman-Van Bavel are the lowest among these methods which are less than 35%,the relative error of is the highest among these methods which is more than 40%.In conclusion,the method of Pristley-Taylor and Penman-Van Bavel are the best methods to calculate ET0in the Yangtze River Basin,the calculation process are simple at the same time.The method of Pristley-Taylor and Penman-Van Bavel can be a simplified recommendation of calculating ET0in the Yangtze River Basin.

climate change;evapotranspiration;models;the Yangtze River Basin;reference crop evapotranspiration; inverse distance weighted interpolation method;space distribution;applicability evaluation

10.11975/j.issn.1002-6819.2016.06.018

S161.4

A

1002-6819（2016）-06-0130-09

2015-09-21

2016-01-25

国家科技支撑计划项目（2015BAD24B01）；农业部旱作节水农业重点实验室基金（HZJSNY201502）；国家自然科学基金项目（51009101）；南方丘区节水农业研究四川省重点实验室开放基金项目（JSSYS2014-C）；四川省软科学研究计划项目（2015ZR0157）

贾 悦（1992-），男，研究方向为节水灌溉理论与新技术，成都四川大学水利水电学院，610065。Email:jiayuescu@163.com

※通信作者：崔宁博（1981-），男，副教授，研究方向为节水灌溉理论与新技术，成都 四川大学水利水电学院，610065。Email：cuiningbo@126.com