基于排队理论的灌区渠系地表水及地下水优化配置模型

杨改强，郭 萍，李睿环，李 茉

（1.中国农业大学水利与土木工程学院，北京 10008；2.太原科技大学环境与安全学院，太原 030024）

基于排队理论的灌区渠系地表水及地下水优化配置模型

杨改强1，2，郭 萍1※，李睿环1，李 茉1

（1.中国农业大学水利与土木工程学院，北京 10008；2.太原科技大学环境与安全学院，太原 030024）

地表水和地下水联合运用于农业灌溉是中国大部分灌区主要采用的灌溉形式，但目前的优化模型对地下水的运用情况过于简化，常采用定值作为优化模型的参数，所以不能真实反映地下水随时间对灌溉面积的影响。该文基于排队理论，研究分析了地下水灌溉的农田面积随等待地表水灌溉的历时的影响，并建立灌区渠系优化配水模型，以灌水历时最短为目标，根据渠首引水、渠系供水、作物用水等方面的用水关系建立约束条件。通过河北石津灌区的实际应用，说明模型方法的可行性，并提出该灌区5条主要干渠的合理优化配水方案。结果显示最优的灌溉历时为25.6 d；干渠B1的灌水周期贯穿了大部分灌水周期，是影响整个系统灌溉效率的关键渠道；子区C5分配的地下水资源较多，该子区的地下水灌溉面积占到了43%。该模型可更加真实地反映用于灌溉的地下水水量随时间变化的不确定性，能够为中国大部分地区建立地表水和地下水联合灌溉优化模型提供方法上的借鉴。

灌区；模型；水资源；排队理论；优化模型；水资源优化配置

杨改强，郭 萍，李睿环，李 茉.基于排队理论的灌区渠系地表水及地下水优化配置模型[J].农业工程学报，2016，32（6）：115-120. doi：10.11975/j.issn.1002-6819.2016.06.016 http://www.tcsae.org

Yang Gaiqiang,Guo Ping,Li Ruihuan,Li Mo.Optimal allocation model of surface water and groundwater based on queuing theory in irrigation district[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE）,2016,32(6): 115－120.(in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2016.06.016 http://www.tcsae.org

0 引言

随着社会经济的快速发展，人们对水资源的需求越来越大。水资源短缺已成为影响水资源可持续发展的主要障碍[1]，尤其是农业水的可用量的持续减少。为缓解农业用水的压力，许多水资源优化技术已经被提出，并取得了可观的研究成果[2]。比如灌区地表水与地下水联合运用模型于上世纪50年代初开始被提出就不断深入研究，在模型结构及耦合技术方面都有着很大的进展[3]。但是地表水和地下水联合运用模型仍存在很多问题，主要表现在对于非线性的模型结构，建立和求解都比较困难，因此在建立模型时往往进行了很多简化[4]。比如对于地下水灌溉量来说，通常在建模时直接给出定值或者通过总灌溉量的比例确定。而实际上，农户是离散分布在灌溉范围内的，相应的用于地下水灌溉的水井也离散于整个灌区。对于大多数中国的灌区，灌溉管理部门可以统一规划地表水的灌溉方案，却无法详细制定地下水的实际使用方案。因为水井离散分布的特点，很多地方不受灌溉管理部门直接管理，农户在地下水的使用上具有很大的随意性[5]。因此也就表现出地下水应用的不确定性[6-7]，在灌溉时期内，地下水的实际应用量会随时间呈逐渐增加的趋势。如何更真实地反映地下水灌溉的实际情况，使优化模型的构架更接近实际，优化结果更具有说服力，将是本文研究的主要问题。

本文采用排队理论来描述地下水用水情况，并根据渠首引水、渠系供水、作物用水等方面的用水关系，建立基于排队理论的优化供水模型。然后通过河北省石津灌区的实际应用，证明模型方法的可行性，提出合理的优化方案。本模型旨在将排队理论应用于灌区的优化供水模型中，达到更真实地反映中国大部分灌区农户离散运用地下水灌溉与统一规划地表水灌溉的情况，并使模型与优化结果更加合理的目的。

1 地下水农业灌溉的排队现象

地下水作为农业灌溉的一种主要水源，不可避免地会纳入水管理中。而近年来，农业、环境和城市等多种用途的水资源需求量不断提高，加剧了地下水的开采量，同时也会由于地下水位下降增加未来的抽水成本[8]。一般而言农户对于地下水的利用，只集中于作物的某几个生长阶段，用水时间较为集中。在表下水可用的情况下，可近似认为地下水灌溉的面积随时间服从泊松分布。因此可以用排队理论来描述地下水用水的变化情况。目前，将排队理论应用于地下水的研究非常少见。仅Batabyal在1995年应用了排队理论研究了系统收益最大化时的地下水供给量及供给速度的问题，其排队模型采用的是仅有一个服务机构的（M/M/1）模型[9]。但是如何将排队理论用于与农业灌溉系统相结合并研究地下水的应用问题，还没有相关的研究成果。

排队现象在现实生活中非常普遍，且排队理论被广泛应用于电子商务、工业制造、企业管理等各类排队模型研究中[10]。排队理论是通过对服务对象到来和服务时间进行科学统计，并研究出包括等待时间、排队长度、忙期长短等在内的数量指标的统计规律。排队系统也称为服务系统，由服务机构和服务对象构成。

在灌溉范围内，从便利性及成本上来说，农户会优先选择地表水。在农作物灌溉时期内，供水渠道不可能对所有子区同时进行灌溉，而作为供水的地下水取水井数量有限，农户作为离散的个体，采用地下水灌溉时必然存在着排队现象。农户即服务对象，地下水取水井即服务机构。一个取水井相当于一个服务机构，灌溉子区内存在多个水井，也就是多个服务机构。假定单位灌溉面积为一个服务对象，相比于整个灌溉面积来说，单位面积显然过小，为计算方便，近似将其假定为无穷个服务对象。农户决定了接受地下水取水井灌溉的时间（进入服务系统的时间），而地下水取水井决定了农户灌溉所花费的时间（占用服务系统的时间）。农户接受地下水取水井灌溉的时间可以认为是随机分布的；地下水灌溉的时间和水井的出水量及农田灌溉的大小等存在一定的比例关系；就单位灌溉面积而言，大范围内地下水灌溉所花费的时间也可以视为随机分布。在灌溉开始时，绝大多数农户仍希望采用地表水灌溉，但如果地表水灌溉的不及时，农户会逐渐加入地下水灌溉的队列。因此，近似假定地下水灌溉满足（M/M/C）：（∞/∞/FCFS）排队模型[11]，表示农户相继进入地下水灌溉队列和灌溉所花费的时间为负指数分布，地下水取水井为多个，系统能够容纳无限个农户，排队服务的规则为先到先服务。因此，农户相继进入地下水灌溉队列的间隔时间t的分布为：

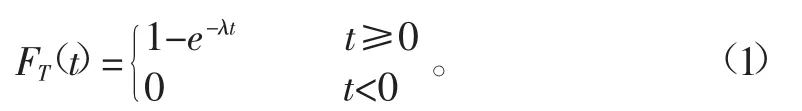
式中λ为单位时间内进入地下水灌溉队列的农户数量，个；t为时间，d。

排队系统中存在某农户数量的概率为：

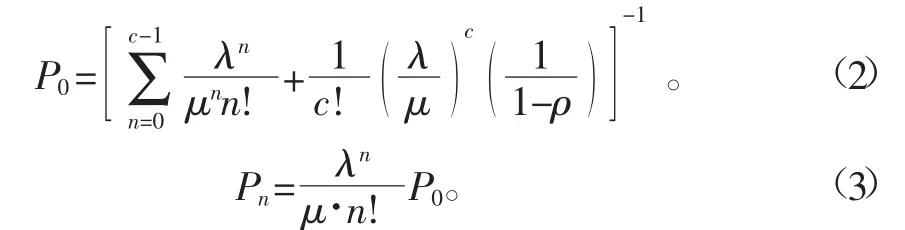
式中c为可用的地下水取水井的数量；μ为单位时间内地下水灌溉完的农户数量；ρ为每个地下水取水井的服务强度；P0为系统中平均有0个农户的概率；Pn为系统中平均有n个农户的概率。

2 配水优化模型

灌区的渠系一般为枝状，包含总干渠、干渠、分干渠、支渠、斗渠、农渠、毛渠等级别。为简化计算，模型仅考虑总干渠和干渠2级渠系，如图1所示。

灌溉水经A1、A2流向AImax，其间分配给各干渠，再分配给相对应的灌溉子区。由于退水渠未参与水量分配，故模型中不考虑该渠段。

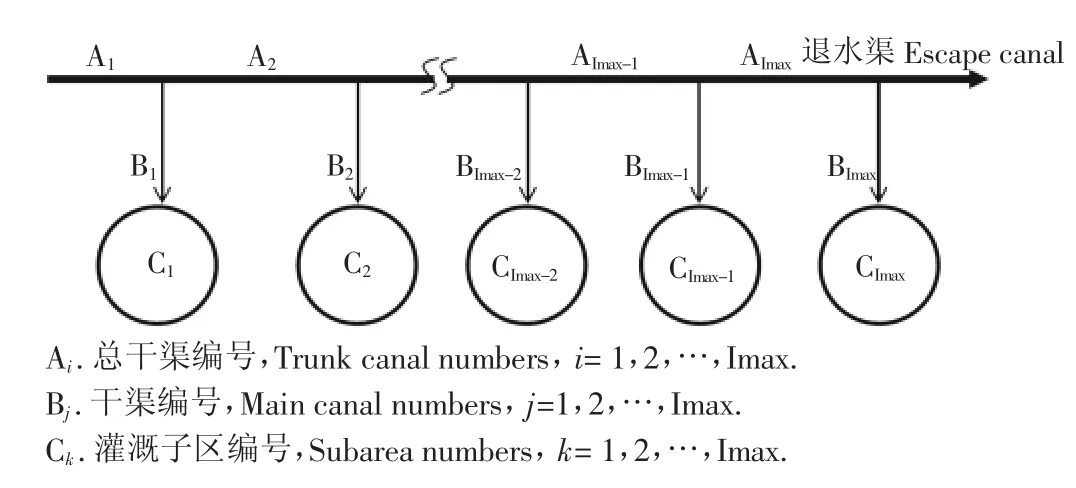
图1 枝状渠系示意图Fig.1 Sketch map of branch canal system

2.1 模型目标

当配水渠道输水能力保持稳定时，配水渠道的输水渗漏损失与输水的持续时间呈单调增的关系，即输水的时间越长，渠道的渗漏损失越大[12]。同时，输水的时间长短也直接影响到渠道的管理成本和电费成本。因此，将在可用水量充足的条件下，按输水时间最短作为流量优化调度的最终目标，从而生成最优配水方案。

模型中定义了2个下标变量，i代表总干渠或干渠的编号，t代表时间。并设Tsi、Tei分别代表干渠Bi开始灌水的时间和结束灌水的时间。则在可用水量充足的条件下，要保证输水时间最短，只需保证所有灌溉子区中最大的Tei最小。即模型目标为

2.2 模型约束条件

模型约束条件包括灌水量、流速、时间等多方面的约束。

1）可用水量约束

研究时段内的总用水量不应超过总渠首允许的引水量。因为所有子区的灌溉水量均需通过总干渠的第一段A1，因此只需考虑段A1在研究内段内的总通过水量即可。

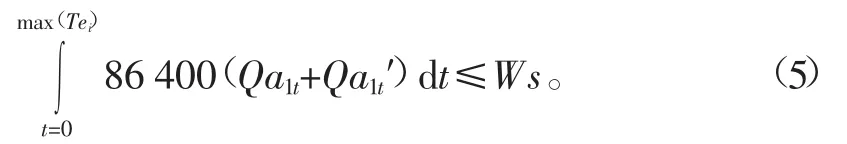
式中Qa1t为t时刻时总干渠A1末端的流量，m3/s；Qa1t′为t时刻时流经总干渠A1的渠道输水损失流量，m3/s；Ws为地表水中可用于灌溉的最大引水量，m3。

假设渠道的总干渠和干渠的衬砌条件相同，根据文献[13]，总干渠的渠道输水损失流量为：

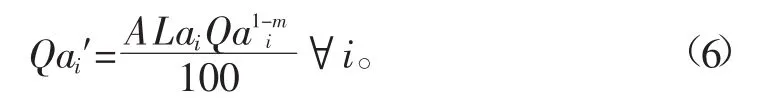
式中A为渠道的渠床透水系数；m为渠床土壤的透水指数；Lai为总干渠Ai的渠道长度，km。

2）总干渠末端流量平衡约束

除去最后一段退水渠，其余总干渠末端的流量均等于该末端所连的干渠渠首流量与下一段总干渠渠首流量之和。

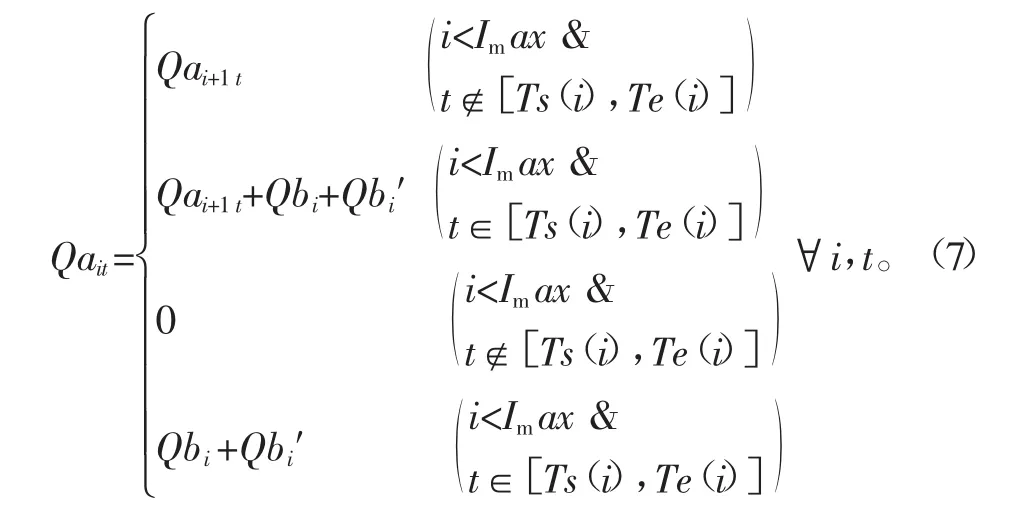
式中Qait为t时刻时总干渠Ai末端的流量，m3/s；Qbi为干渠Bi末端灌溉时的流量，m3/s；Qbi′为灌溉时流经干渠Bi的渠道输水损失流量，m3/s。

干渠的渠道输水损失流量为：

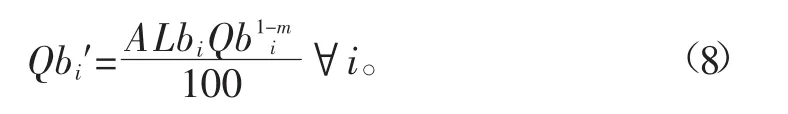
式中Lbi为干渠Bi的渠道长度，km。

3）总干渠流量约束

每一段总干渠的渠首流量应满足该段的设计流量。

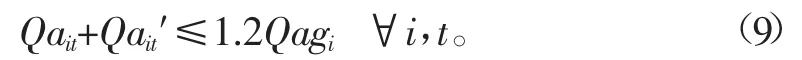
式中Qagi为总干渠Ai的渠道设计流量，m3/s，其值不超过1.2倍的设计流量。因为石津灌区的主干渠除向周边农田提供灌溉用水处，还承担着南水北调等输水任务，所以本文为简化模型，仅考虑该渠道的供水上限限制，即1.2倍的设计流量。

4）干渠流量约束

每一段干渠的渠首流量也应满足该段的设计流量。

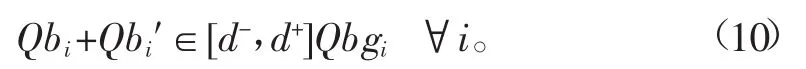
式中Qbgi为干渠Bi的渠道设计流量，m3/s；[d-，d+]为设计流量的比值范围，一般d-取0.8，d+取1.2。

5）渠道的灌水时间约束

对于任意渠道，灌水结束的时间必定大于开始灌水的时间。

6）子区的灌溉面积约束

根据假定的地下水灌溉的（M/M/C）：（∞/∞/FCFS）排队模型，则某子区在某时刻完成或即将采用地下水灌溉的农田数量为表示某子区在某时刻t加入地下水灌溉队列的农田数量，影响参数为λi和时间t。如果灌溉区域仅采用地下水或地表水分别灌溉，不存在未灌溉面积，则地表水灌溉的面积比例相当于并且地表水灌溉的面积应满足地表水灌溉的设计保证率。式中Argi为子区Ci中地下水灌溉的面积，hm2；λi为子区Ci的平均到达率，即单位时间内加入地下水灌溉队列的面积；Pr为地表水灌溉的设计保证率，%。

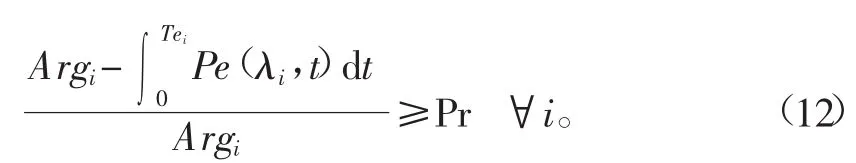
上式可变形为

式中F表示地下水灌溉队列的概率分布函数，影响参数为Argi、λi和Tei。

7）子区的灌溉水量约束

子区的灌溉水量包括地表水和地下水两部分，总水量应满足该子区的设计灌溉水量。

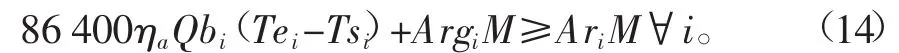
式中ηa为干渠出水的灌溉效率；Ari为研究作物在子区Ci的灌溉面积，hm2；M为研究作物的灌溉定额，m3/hm2。

8）地下水可水量约束

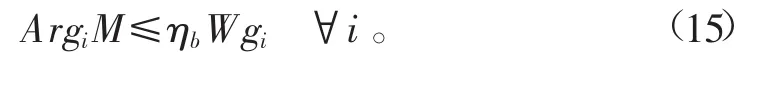
地下水的灌溉量不应大于当地可允许的地下水开采量。式中ηb为地下水的灌溉效率；Wgi为子区Ci可允许的地下水用水量，m3。

9）非负约束

各决策变量的技术性约束。

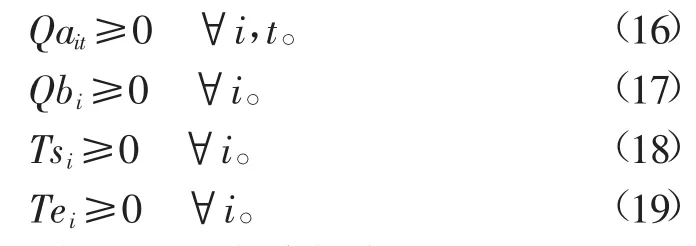
式中Qait为t时刻时总干渠Ai末端的流量，m3/s；Qbi为干渠Bi末端灌溉时的流量，m3/s；Tsi为干渠Bi开始灌水的时间，d；Tei为干渠Bi结束灌水的时间，d。

2.3 模型的求解

由于上述模型中变量多，约束多，模型的结构复杂，且具有非线性的特点，不易直接求解得到优化方案。对于这类模型的求解，国内外的学者也进行过大量的研究，并提出很多可行的算法，如遗传算法[14]、蚁群算法[15]、粒子群算法[16]、人工蜂群算法[17]、人工鱼群算法[18]等。这些算法都可以有效地求解上述模型。其中粒子群算法出现较早，它比遗传算法规则更加简单，无需进行交叉和变异操作。另外其它很多算法也是基于粒子群算法衍化或与其它优化算法理念相结合而产生的。粒子群算法容易实现、精度高、技术也比较成熟，已成功应用于解决多种不确定问题[19-20]。因此本文选择粒子群算法对模型进行求解[21]，其程序流程图如图2所示。

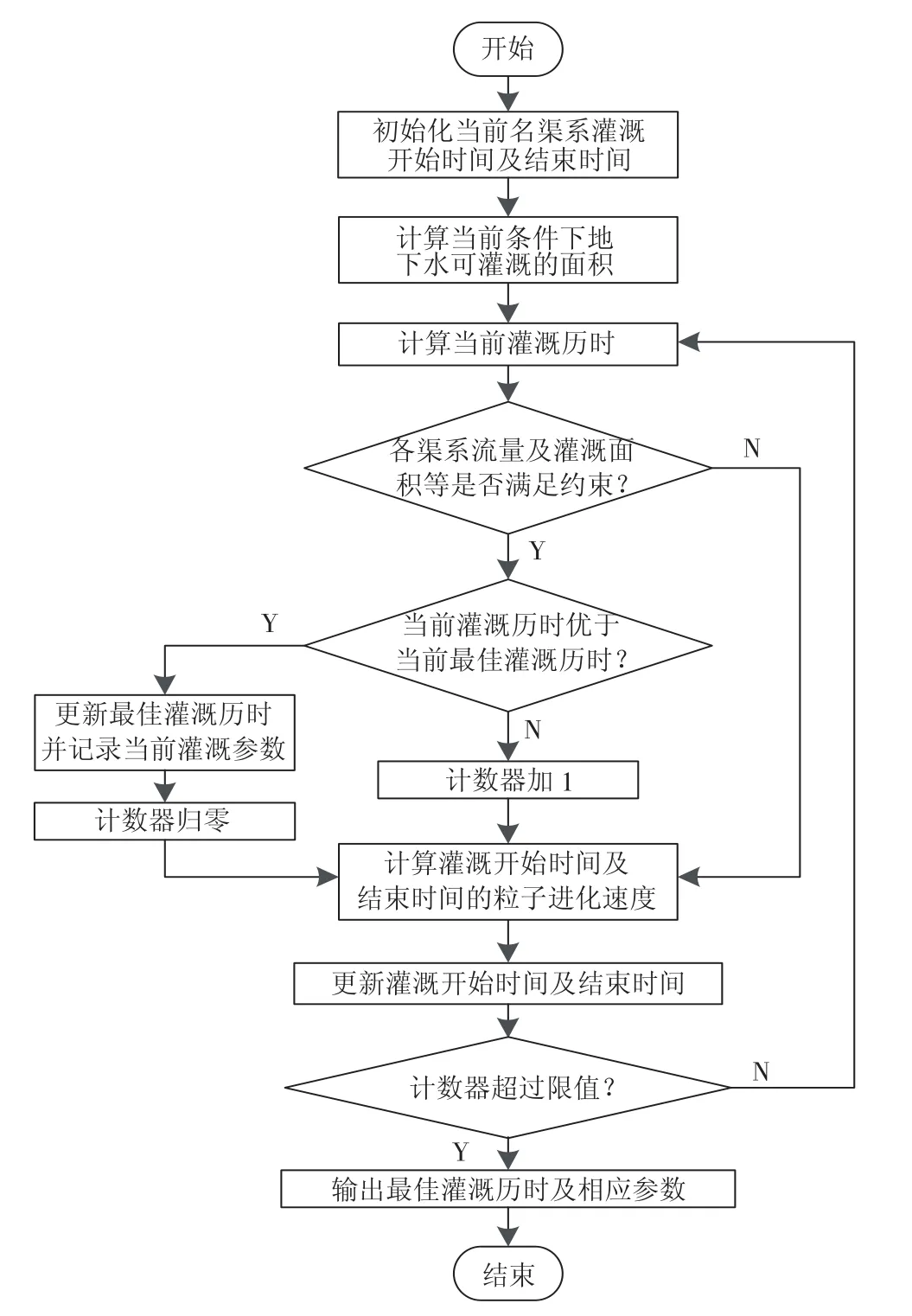
图2 程序流程图Fig.2 Program flow chart

3 实例应用

为证明上述模型的实用性，本文选择河北省石津灌区的其中5个主要干渠控制范围作为研究区域。石津灌区位于中国河北省中南部，其灌溉渠系的分布如图3所示。设计灌溉面积1.67×104hm2，总干渠为自西向东流向，农业灌溉主要集中总干渠以南的区域[22]。

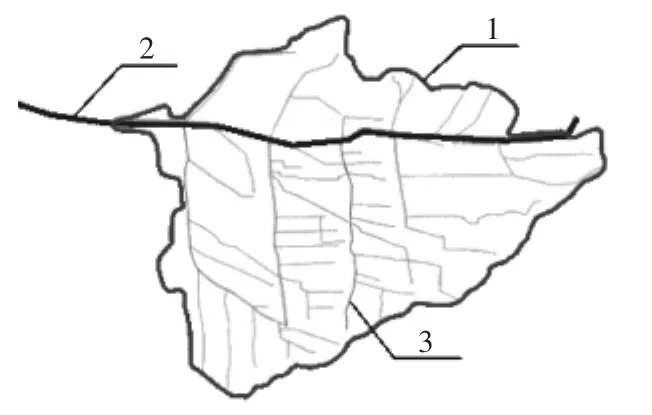
图3 渠系分布简图Fig.3 Schematic diagram of canal distribution

渠系等基础数据选自该灌区《续建配套与节水改造规划报告》中对2015年的规划数据。渠道的主要设计技术参数如表1所示。总干渠（A1-A5）主要承担输配水任务，为简化模型，忽略主干渠直接浇灌的农田面积，并将各渠系控制灌溉面积集中到干渠一级（B1-B5）。

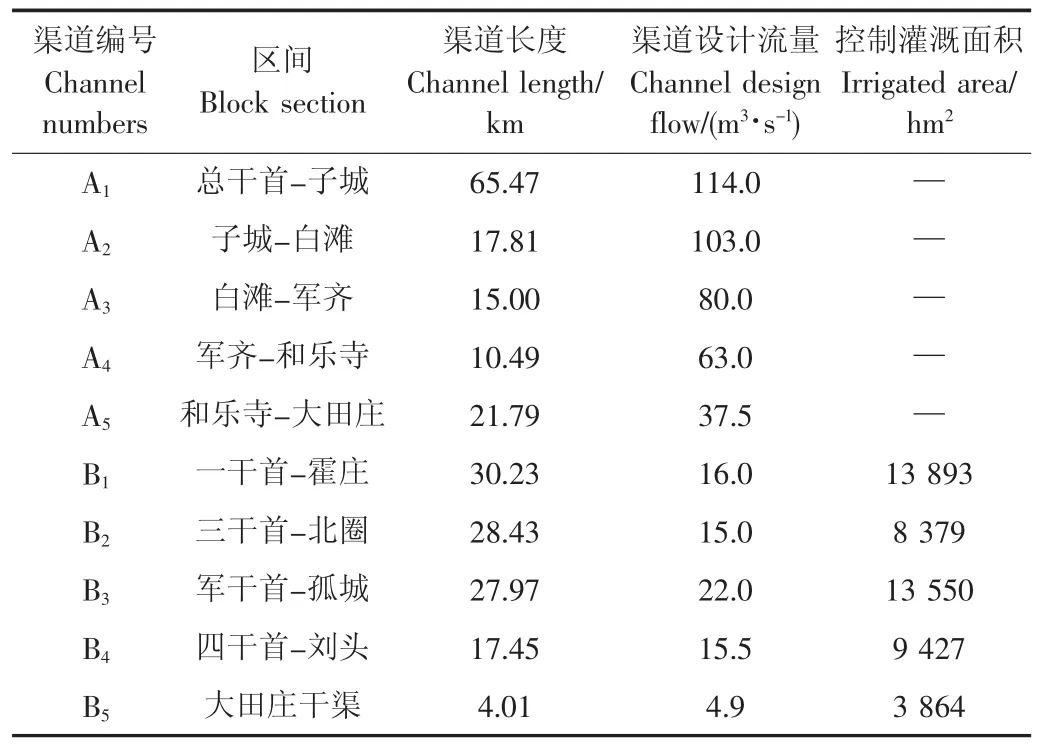
表1 渠道主要设计参数Table 1 Main design parameters of canals

模型的作物仅考虑冬小麦，设计灌溉定额为2155.5m3/hm2，设计保证率75%。干渠以下的地表水利用系数为0.783，井水的利用系数为0.85。渠床透水系数取0.7，土壤的透水指数取0.3。经优化求解后，得到干渠的配水方案与图4所示。

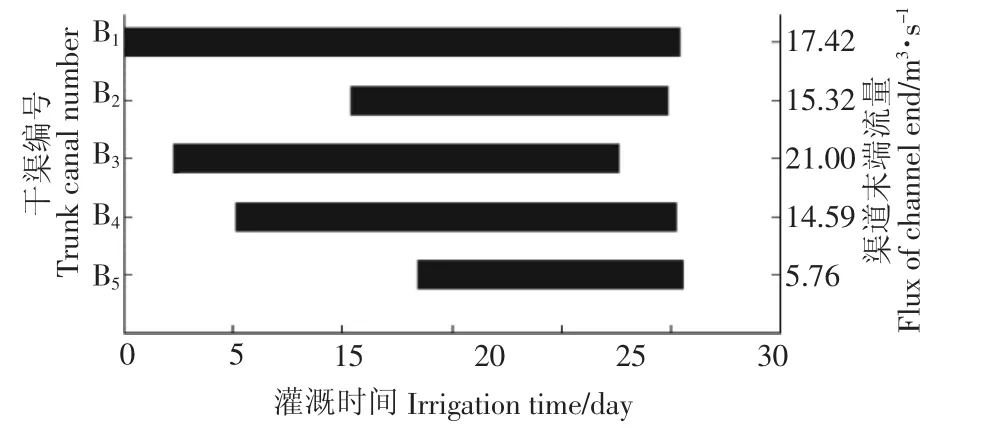
图4 干渠配水方案Fig.4 Water allocation scheme of main channel

经过优化后的整个灌水周期为25.6 d，而历史的灌水周期约在30～50 d，平均40 d左右。实际情况下，灌溉期间可能会突发暴雨、停电等偶然事件，这些都可能导致灌水周期的延长。而模型是在理想条件下得到的，并未考虑到其它的意外情况，所以优化的结果要明显好于实际的操作。

从图4中也可以看到，干渠B1的灌水周期贯穿了大部分灌水周期。由于干渠B1的设计流量过小，只有16 m3/ s，而其控制灌溉面积在整个研究区域内最大，为13 983 hm2，因此造成该干渠的灌历时稍长。若进一步优化渠系，可以考虑改善干渠B1的输水条件，提高它的设计流量。另外4条干渠在渠水周期内的灌溉时间调整相对自由，可适当推迟灌水时间。其中B2和B5的灌溉开始的时间较晚，分别为10.4和13.4 d。按照排队理论的观点，推迟灌溉的时间越久，因等不及地表水灌溉而转向采用地下水灌溉的农户也就越多，也就是采用地下水灌溉的灌溉面积越大。只要在地下水允许的范围内，推迟灌溉是可取的。这样可以适当减少灌区管理部门的输水成本和地表水的消耗，对南水北调其周边城镇及工业用水也都有着积极的作用。在5条干渠中，干渠B5的灌溉历时最短，只需12.2 d，这说明干渠B5的供水能力在这几条干渠中是最强的，这也和干渠B5的控制灌溉面积与最初渠系设计时的灌溉面积相比变得更小有关系。B5的控制灌溉面积最小，并且有减少的趋势，该段的供水能力也就表现的比较越强。在13.4～22.7 d，所有干渠均处于工作状态，这段期间是灌溉集中的时间，整个系统处于满负荷运行，因此在这段时间内，维护整个灌溉系统的正常运行尤为重要，一旦发生停电供水、化学危险品进入水体等偶然事件，其影响将是大范围的。

从优化结果不难看出，所有干渠的优化流量均接近设计时的流量，其中B1和B5的优化流量要高于设计流量，但在1.2倍的设计流量限值之内。如需提高整个系统的灌溉能力，应从这2条干渠着手，但由于干渠B5所控制的灌溉面积最小，因此改造干渠B5的供水能力带来的效果可能并不如改造干渠B1的效果好。

由于该渠系的主干渠是南水北调的配套工程之一，还负责周边城市及地区的生活、工业等用水，所以主干渠的设计流量足够大，远超系统在满负荷运行时的灌溉流量。即使在集中供水的期间内，也不会对整个农业供水系统造成太大的压力。

在各子区内，不同类型的水源控制面积比例如图5所示。子区C1离总干渠渠首最近，分配的水量也比较多，从灌溉开始到结束期间全部采用地表水进行灌溉。而子区C5离总干渠渠首最远，将充分利用地下水灌溉，该子区地下水灌溉面积可达到该子区的43%。整体上看，所有子区都是以地表水灌溉为主，地表水控制的灌溉面积占到了93%。在该研究区域内，地表水仍是灌溉的主要来源。

对于该灌区，本研究通过合理调节各渠系的流量和供水时间，充分利用了地下水资源，降低了系统的供水成本，实现了更大的经济效益。

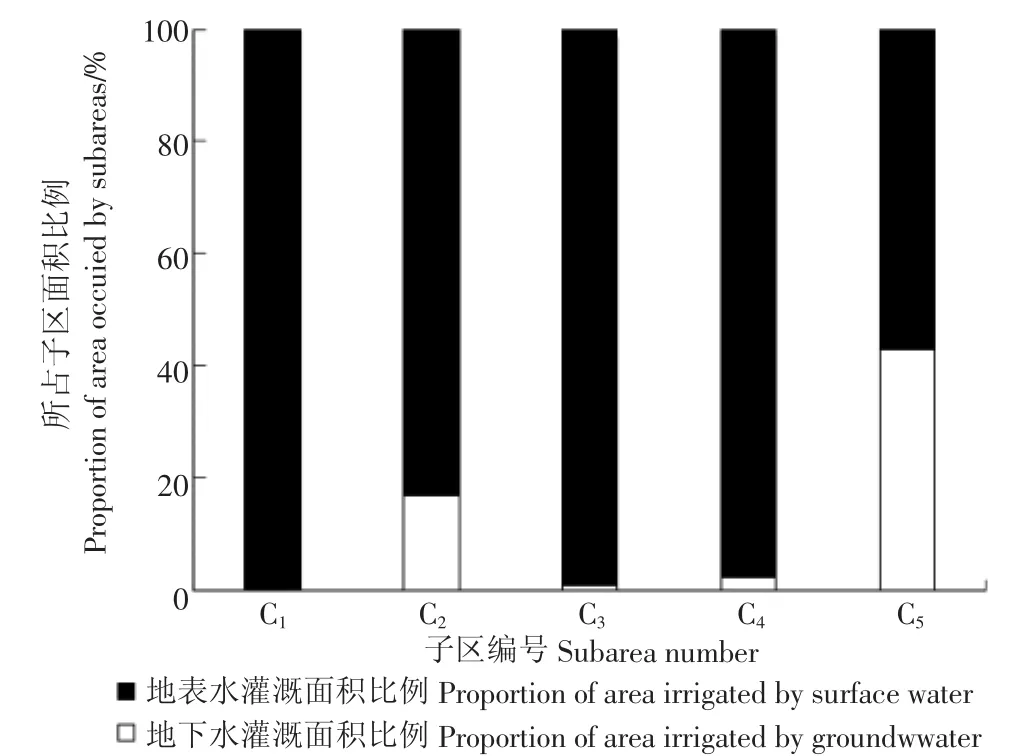
图5 不同类型水源灌溉面积所占比例Fig.5 Proportion of irrigation area for different water source

4 结论

1）优化结果显示最优的灌溉历时为25.6 d，而实际的灌水周期为30～50 d，优化结果优于目前的实际情况。

2）干渠B1的灌水周期贯穿了大部分灌水周期，且灌溉时的干渠流量高于该渠的设计流量，是影响整个系统灌溉效率的关键渠道。如后期进一步优化灌溉渠系，则干渠B1的流量是优化的关键。

3）子区C5离总干渠渠首最远，地下水资源利用的较多，地下水灌溉的面积可达该区的43%。但该区所控制的灌溉面积最小，因此对整个灌溉系统的影响也较小。

本文应用排队理论对采用地下水灌溉的农户数量作分布描述，并结合渠首引水、渠系供水、作物用水等方面的用水关系建立了基于排队理论的优化模型。该模型能够反映灌区中运用地下水灌溉随时间变化的不确定性，适用于地下水抽水井随机分布，地下水的抽取无需统一安排的灌区，且灌区为地下水地表水联合灌溉，而不是单纯的渠灌或井灌区。本文为证明其实用性，模型考虑了主干渠和干渠2级渠系。如需更加精确的优化结果，需要对多级渠系（毛渠、支渠、斗渠等）详细划分控制灌溉面积并统计其用水数据。

[1]Lu H W,Huang G H,He L.Development of an interval-valued fuzzy linear-programming method based on infinite α-cuts for water resources management[J].Environmental Modelling& Software,2010,25(3):354-361.

[2]Guo Ping,Chen Xiaohong,Tong Ling,et al.An optimization model for a crop deficit irrigation system under uncertainty[J]. Engineering Optimization,2014,46(1):1-14.

[3]Banks H O.Utilization of underground storage reservoirs[J]. Transactions of the American Society of Civil Engineers,1953, 118(1):220-234.

[4]岳卫峰，杨金忠，占车生．引黄灌区水资源联合利用耦合模型[J]．农业工程学报，2011，27(4):35-40．Yue Weifeng,Yang Jinzhong,Zhan Chesheng.Coupled model for conjunctive use of water resources in the Yellow River irrigation district[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）,2011,27 (4):35-40.(in Chinese with English abstract)

[5]胡怀亮，秦克丽，张国岑．河南省水井工程布局合理性研究[J]．灌溉排水学报，2014，33(3):78－82．Hu Huailiang,Qin Keli,Zhang Guocen.Study on the layout rationality of wells in henan province[J].Journal of Irrigation and Drainage,2014,33(3):78-82.(in Chinese with English abstract)

[6]Li Mo,Guo Ping.A multi-objective optimal allocation model for irrigation water resources under multiple uncertainties[J]. Applied Mathematical Modelling,2014,38(19－20):4897-4911.

[7]Zhang Liudong,Guo Ping,Fang Shiqi,et al.Monthly optimal reservoirs operation for multicrop deficit irrigation under fuzzy stochastic uncertainties[J].Journal of Applied Mathematics, 2014,2014:1-11.

[8]Medellin A J,MacEwan D,Howitt R E,et al.Hydro-economic analysis of groundwater pumping for irrigated agriculture in California′s Central Valley,USA[J].Hydrogeology Journal, 2015,23(6):1205-1216.

[9]Batabyal A A.The queuing theoretic approach to groundwater management[J].Ecological modelling,1996,85(2):219-227.

[10]Tan Wenan,Xu Wei,Yang Fujun,et al.A framework for service enterprise workflow simulation with multi-agents cooperation[J]. Enterprise Information Systems,2013,7(4):523-542.

[11]Ma M J,Yue D Q,Zhao B.Reliability analysis of machine interference problem with vacations and impatience behavior[C]// Zhang D.Industrial,Mechanical and Manufacturing Science．Boca Raton:CRC Press,2015：53-58.

[12]高伟增，余周，汪志农．基于复合基因编码的渠系水资源智能优化研究[J].灌溉排水学报,2011(5)：111-115. Gao Weizeng,Yu Zhou,Wang Zhinong.Solving optimal water distribution by inlelligence with comblex gene.Journal of Irrigation and Drainage[J].2011(5):111-115.(in Chinese with English abstract)

[13]汪志农．灌溉排水工程学[M].北京:中国农业出版社,2000.

[14]Venkatraman S,Yen G G.A generic framework for constrained optimization using genetic algorithms[J].Evolutionary Computation, IEEE Transactions on,2005,9(4):424-435.

[15]Colorni A,Dorigo M,Maniezzo V,et al.Ant system for job-shop scheduling[J].Belgian Journal of Operations Research,Statistics and Computer Science,1994,34(1):39-53.

[16]Eberhart R C,Kennedy J.A new optimizer using particle swarm theory[C]//CrossRef.Proceedings of the sixth international symposium on micro machine and human science.Piscataway: IEEE Press,1995,1:39-43.

[17]Karaboga D,Akay B.A comparative study of artificial bee colony algorithm[J].Applied Mathematics and Computation,2009,214 (1):108-132.

[18]Li Xiaolei,Shao Zhijiang,Qian Jixin.An optimizing method based on autonomous animats:fish-swarm algorithm[J].System Engineering Theory and Practice,2002,22(11):32-38.

[19]Moghaddam B F,Ruiz R,Sadjadi S J.Vehicle routing problem with uncertain demands:An advanced particle swarm algorithm [J].Computers&Industrial Engineering,2012,62(1):306-317.

[20]Shirazi M J,Vatankhah R,Boroushaki M,et al.Application ofparticle swarm optimization in chaos synchronization in noisy environment in presence of unknown parameter uncertainty[J]. Communications in Nonlinear Science and Numerical Simulation,2012,17(2):742-753.

[21]陈晓楠，段春青，邱林，等．基于粒子群的大系统优化模型在灌区水资源优化配置中的应用[J].农业工程学报，2008，24 (3)：103-106. Chen Xiaonan,Duan Chunqing,Qiu Lin,et al.Application of large scale system model based on particle swarm optimization to optimal allocation of water resources in irrigation areas[J]. Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）,2008,24(3):103-106.(in Chinese with English abstract)

[22]Yang Gaiqiang,Guo Ping,Huo Lijuan,et al.Optimization of the irrigation water resources for Shijin irrigation district in north China[J].Agricultural Water Management,2015,158:82-98.

Optimal allocation model of surface water and groundwater based on queuing theory in irrigation district

Yang Gaiqiang1,2,Guo Ping1※,Li Ruihuan1,Li Mo1
(1.College of Water Resources and Civil Engineering,China Agricultural University,Beijing 100083,China;2.Institute of Environmental Science,Taiyuan University of Science and Technology,Taiyuan 030024,China)

The conjunctive use of groundwater and surface water for agricultural irrigation is one of the main irrigation patterns of most irrigation districts in China.The input parameters of current optimization models of groundwater are usually crisp numbers,which are too simple to truly reflect the impacts of the groundwater utilization variance on irrigation areas over time.In order to obtain more reasonable results,this study aims to develop a model for the conjunctive use of groundwater and surface water model considering the uncertainties of the application of groundwater.In general,there are only a few growth stages during which crops are irrigated by groundwater,and the relationship between crop areas irrigated by groundwater and the duration of surface water irrigation can be described as Poisson distribution.The queuing theory was used to express the uncertainty of the groundwater exploitation,and the(M/M/C):(∞/∞/FCFS)model was adopted.Based on the analyses of the queuing behavior,an optimal irrigation water allocation model was established.The model takes into account two levels of canal system including main canals and trunk canals.The objective of the model is to minimize irrigation duration,subjected to a series of constrains including surface water availability,groundwater availability, permitted flux of main canals,permitted flux of trunk canals,irrigation duration of channels,irrigation area of subareas,etc. It is difficult to solve the model using conventional solution method because of the complexity and the nonlinearity of the structure of the model.Therefore,the particle swarm optimization algorithm which can solve above problems was adopted to obtain the optimal water allocation schemes for the five main channels.Results from applying the model to a case study in the Shijin Irrigation District in Hebei demonstrate the feasibility and the applicability of the developed model.The results showed that the optimal irrigation duration is 25.6 days which is better than the previous irrigation durations(40 days on average).Channel B1is the key channel for the efficiency improvement of the whole irrigation system since its irrigation period occupies most of the optimal irrigation duration.The reason is that the design flux of channel B1(16 m3/s)is small, while its controlled irrigation area(13 983 ha)is the largest among all subareas.The other channels are free in the adjustment of irrigation time.Channel B2and B5can be irrigated over a few days,which are 10.4 and 13.4 days.Channel B5has the shortest irrigation duration(12.2 days),which illustrates that water supply capacity of channel B5is the strongest compared with other irrigation areas in all channels.All channels are under full load working conditions during 13.4～22.7 days,thus it is particularly important to maintain the operation of the whole irrigation system.Subdistrict C1can be irrigated by surface water during the whole period because it is the nearest to the canal head of the main canal.Subdistrict C5is allocated with relatively more amounts of groundwater and its irrigated area by groundwater accounts for 43%of the whole irrigation area.This is because subdistrict C5is farthest to the canal head of the main canal and has the minimum surface water use efficiency.The flux of all the canals are approximately equal to the corresponding design values,among which, the flux of B1and B5are higher than their design values but within the scope of 1.2 times of the design values.Accordingly, the water supply capacity of these two canals should be first adjusted in terms of improving the irrigation capacity of the whole system.However,as the area of B5is the smallest,leading to the adjusting effect of B5may not be as obvious as that of B1.Overall,most of the subareas are irrigated by surface water,occupying 93%of whole irrigation area.The study can reflect the variance of groundwater for irrigation over time and provide modelling reference for the establishment of the conjunctive use of surface water and groundwater in most irrigation districts of China.

irrigation district;models;water resources;queuing theory;optimization model;water resources optimal allocation

10.11975/j.issn.1002-6819.2016.06.016

TV213.9

A

1002-6819（2016）-06-0115-06

2015-09-21

2016-01-28

农业部公益项目（201203077）；国际科技合作项目（2013DFG70990）；国家自然科学基金（51321001）

杨改强，男（汉族），山西忻州人，博士生，主要从事水资源规划与管理方面的研究。北京 中国农业大学水利与土木工程学院，100083。Email：ygq99＠163．com

※通信作者：郭 萍，女（汉族），北京人，博士生导师，加拿大里贾纳大学博士，主要从事水资源规划与管理、模型与优化以及决策支持系统的研究。北京 中国农业大学水利与土木工程学院，100083。

Email：guop@cau.edu.cn