基于人工鱼群算法的车辆平顺性优化分析
2016-05-17范政武
范政武,王 铁,陈 峙
(太原理工大学车辆工程系,太原 030024)
基于人工鱼群算法的车辆平顺性优化分析
范政武,王 铁,陈 峙
(太原理工大学车辆工程系,太原 030024)
平顺性是汽车重要特性之一,平顺性优化分析属于组合优化问题,同时其非线性特性导致优化实质上是一个非线性多峰的优化问题,为了有效解决此类复杂优化的求解问题,近年来基于随机搜索优化算法建立了一种新型的人工鱼群算法。该文将人工鱼群算法应用到汽车平顺性优化分析研究中,以某8×4载货车为研究对象,建立9自由度汽车平顺性模型,对影响汽车平顺性的重要参数进行优化分析。优化结果表明,加速度均方根平均下降16.82%,在60 km/h时下降最大,加速度均方根下降21.24%,有效提高了重型车的平顺性能。因此,利用该模型可对汽车平顺性进行预测或评估。
农业机械;模型;优化;平顺性;优化分析;鱼群算法;应用
范政武,王 铁,陈 峙.基于人工鱼群算法的车辆平顺性优化分析[J].农业工程学报,2016,32(6):107-114.doi:10.11975/j.issn.1002-6819.2016.06.015 http://www.tcsae.org
Fan Zhengwu,Wang Tie,Chen Zhi.Vehicle ride comfort analysis and optimization based on artificial fish swarm algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2016,32(6):107-114.(in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2016.06.015 http://www.tcsae.org
0 引言
重载车辆的行驶平顺性不仅决定了驾驶的舒适性而且影响货物安全可靠的运输。国内外学者对平顺性的仿真优化做了大量的研究。文献[1]通过ADAMS建立相关仿真模型,应用响应面法对基本参数进行了优化。文献[2]利用具有紧支撑正交特性的Daubechies小波和最小二乘法原理辨识油气悬架物理参数,借助遗传算法优化油气悬架的物理参数,达到了改善平顺性的目的。文献[3]以1/2汽车8自由度振动系统模型为研究对象,基于悬架参数建立数学模型,采用微粒群算法,优化相关参数,改进了车辆的行驶平顺性。文献[4]运用多种群遗传算法和模糊理论,以轮胎的刚度和阻尼、簧上质量为模糊变量,进行了双层嵌套的不确定性优化。文献[5]针对车辆主动悬架系统的控制,提出一种非线性控方法,应用粒子群算法对控制器的增益进行优化,寻求主动悬架系统核心参数的平衡。文献[6]建立了车辆半主动悬架的模型,提出了模糊逻辑控制,应用粒子群算法优化模糊逻辑控制的比例因子。文献[7]研究了汽车平顺性分析中时域法和频域法的对比,结果表明各种算法计算结果差别不大但各有特点。
本文在建立汽车平顺性模型,应用人工鱼群智能优化算法,以驾驶员座椅处垂向加速度为优化目标,把前后悬架刚度和阻尼作为控制设计变量,对车辆平顺性进行分析和优化。人工鱼群算法(artificial fish school algorithm,AFSA)是2002年由李晓磊博士提出的一种基于动物群体行为的智能优化算法[8],近几年来得到了广泛的应用。
1 模型建立
若要准确地分析汽车的振动响应,首先应建立合理的动力学模型,模型建立时所考虑因素的多少与计算精度有很大关系,由于汽车各部件振动情况十分复杂,欲通过一个完整的模型全面反映汽车的振动特性是比较困难的。因此,在研究问题时,需根据问题的主次因素,对振动系统进行适当的简化。通过对汽车在行驶过程中能量分布的分析,将汽车振动系统简化为具有四轮输入的1/2汽车9自由度动力学模型,其整车参数表见表1,某8×4自卸车9自由度振动力学模型如图1所示。
针对本文9自由度振动力学微分方程,系统的动能T、势能U和耗散能D分别如下公式所示[9]:
其中M,C,K分别是9行9列的质量矩阵、阻尼矩阵、刚度矩阵;KF是9行9列的轮胎刚度矩阵,Z,,分别为位移、速度、加速度列向量;Q为路面激励向量。其中位移向量为Z=[Z1,Z2,Z3,Z4,Z5,θ1,θ2,θ3],路面激励向量为Q=[q1,q2,q3,q4]T。
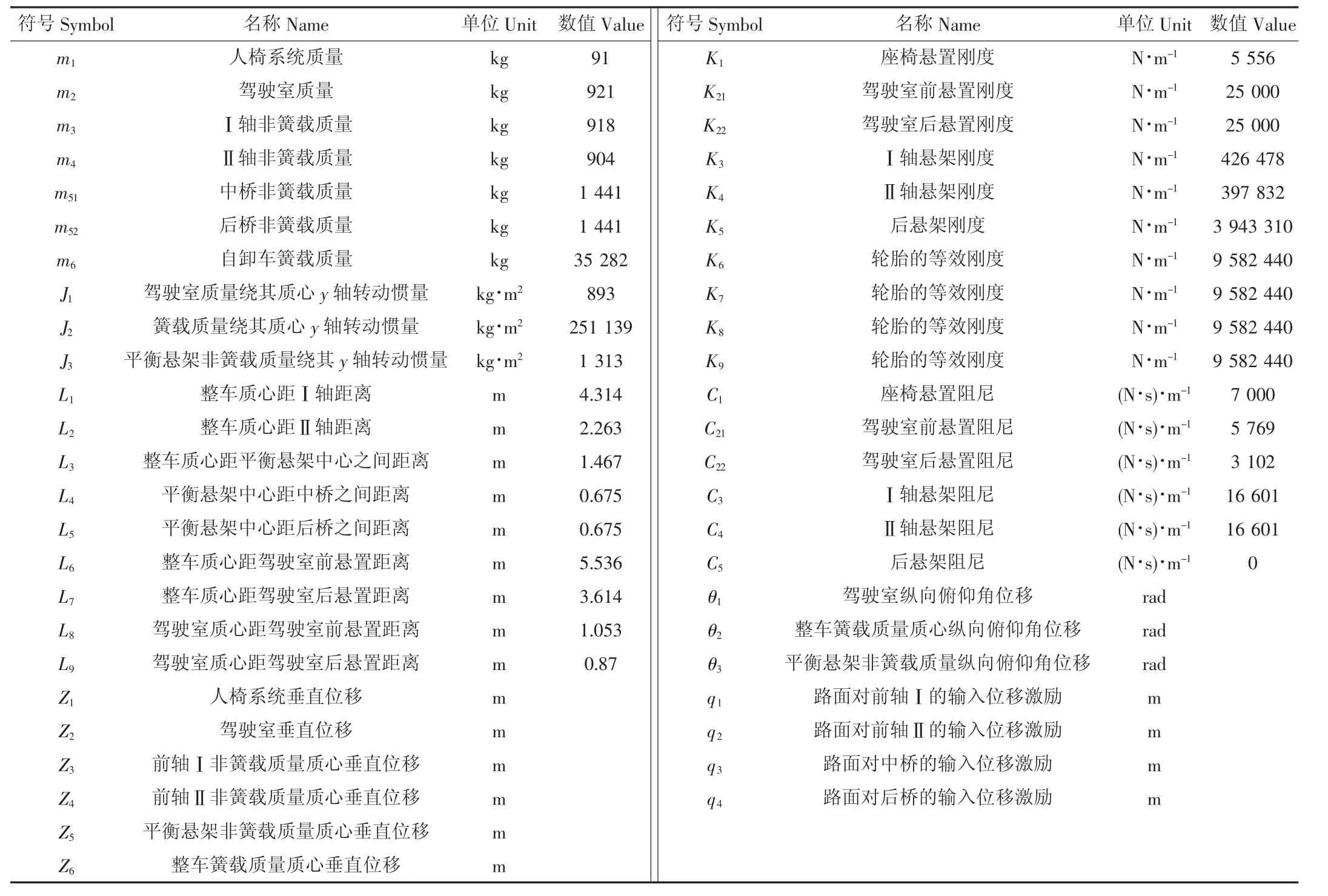
表1 车辆参数表Table 1 Vehicle parameter table
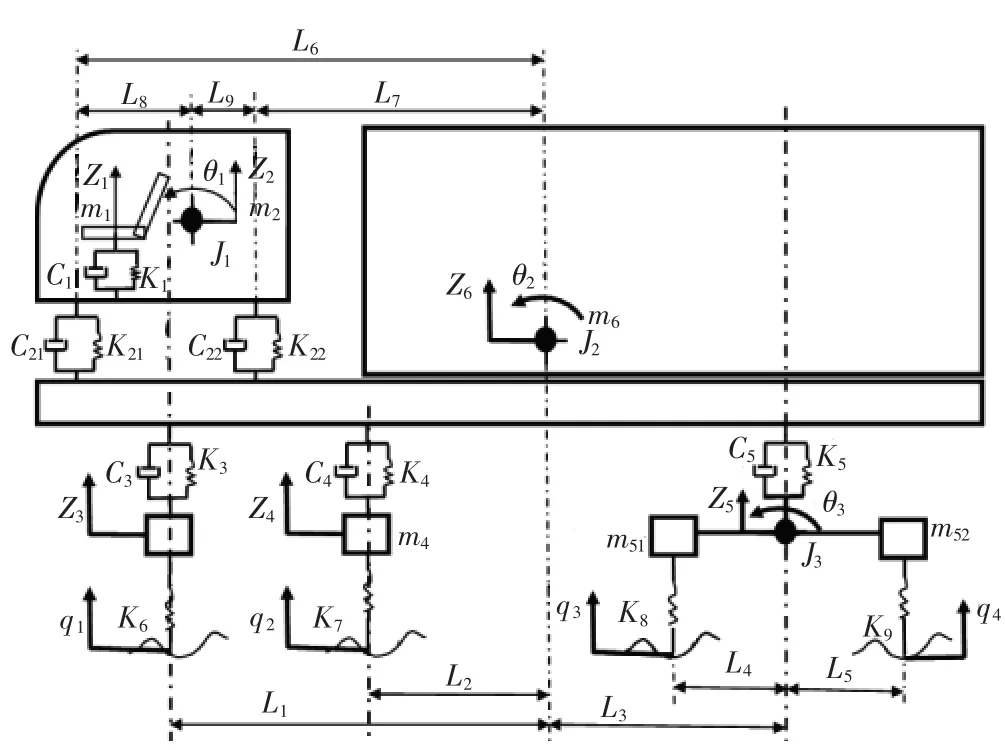
图1 某8×4自卸车9自由度振动力学模型Fig.1 8×4 dump truck 9 degrees of freedom vibration mechanics model
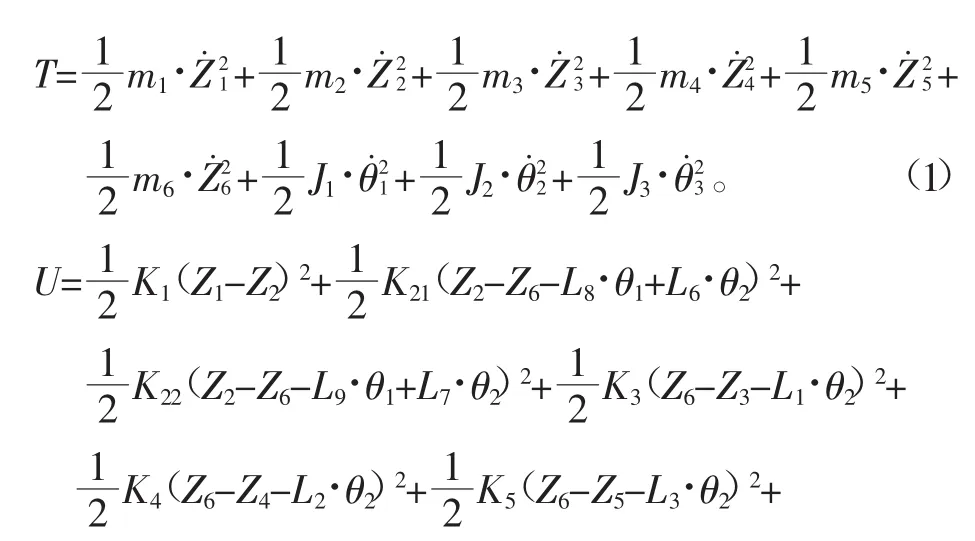

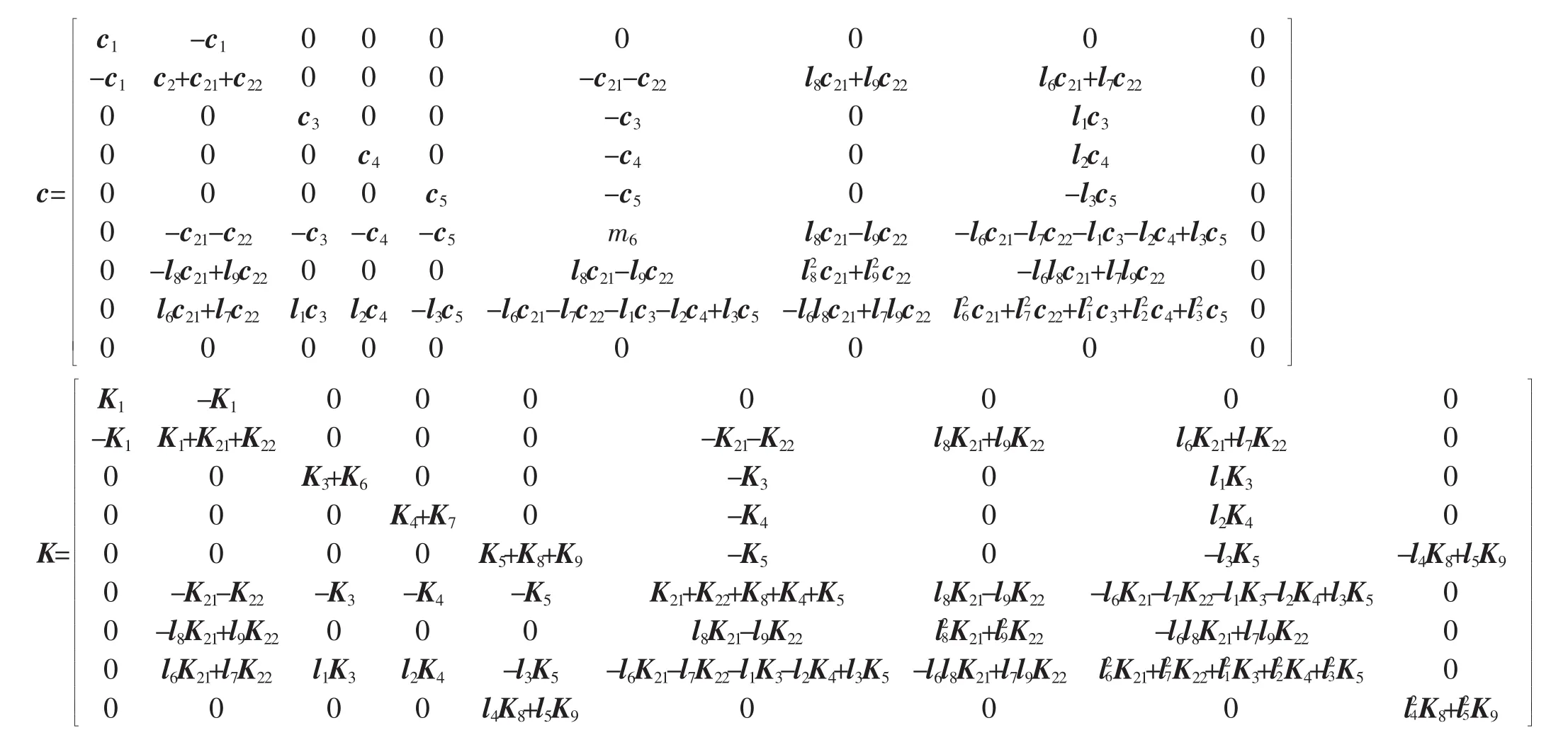
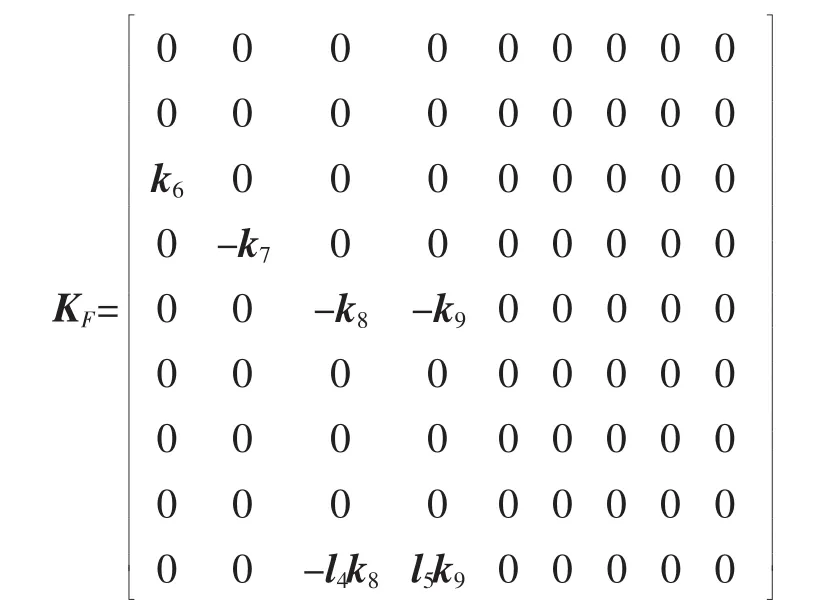
左右轮辙的不平度相同,汽车对称于其纵轴线,则汽车运行时,车身仅考虑垂直振动及俯仰振动。又设后面的车轮行驶在前轮的轮辙上,车轮轮辙激励模型为[10]:
式中α为路面等级相关的常数,本文选取路面等级为C(α=0.121(m-1));u为车速,Δi为延迟时间,Δi=L1i/u,L1(ii= 2,3,4)为二、三、四轴与一轴的距离。
图2是在C路面等级,车速u=70 km/h的条件下4个车轮的路面激励时域仿真。从图中可以看出,q1,q2,q3,q4的变化波形基本相同,只是在时间上有滞后。路面随机激励的位移变化范围为:|Q|<0.02 m。
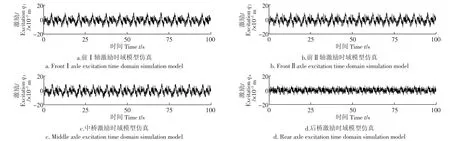
图2 路面激励时域模型仿真Fig.2 Road surface excitation time domain simulation model
2 仿真分析
为进行汽车平顺性仿真,在Matlab中开发了相应的仿真程序。选取C级公路,仿真不同速度下车身座椅处垂直加速度,时域和频域的仿真结果如图3。
图3分别是是以20、40、60、80、100和120 km/h的车速,在C级路面上进行的频域和时域仿真结果,可以看出不同车速下仿真曲线的变化趋势是一致的,但不同车速其车身座椅处的垂直加速度是不同的。图中显示随着车速的增加,车身座椅处的加速度在增加,如20 km/h时,加速度(峰值)最大可达到4.75 m/s2,120 km/h是加速度(峰值)最大可达到5.43 m/s2。通常载货汽车的整车平顺性评价指标采用车身座椅处加速度均方根值,不同车速下的车身座椅处加速度均方根值仿真结果如图4。
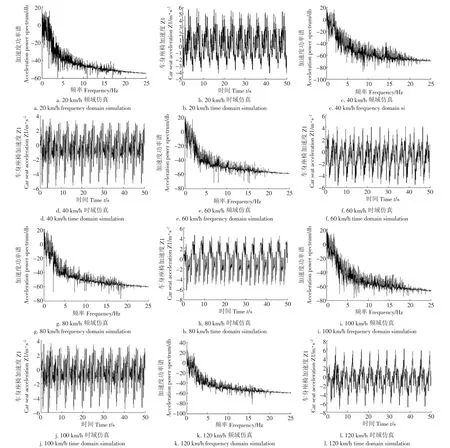
图3 车身座椅垂直加速度频域和时域仿真Fig.3 Body seat vertical acceleration frequency domain and time domain simulation
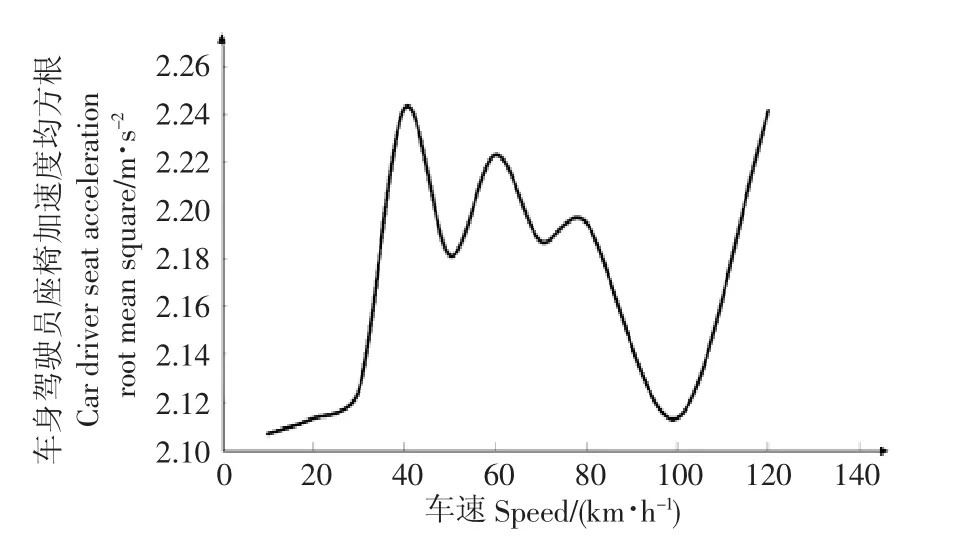
图4 车身座椅垂直加速度均方根Fig.4 Vertical acceleration root mean square of body seat
从图4可以看出,整体上驾驶员座椅处垂直振动加速度随车速增加而变大,整车平顺性也将变差。尤其是低速段和高速段加速度变化更加明显,而在40~80 km/h这一速度段,加速度变换比较平缓。这说明要保持较好的经济性和平顺性,车速应保持在中速段,这与重型汽车实际运行速度相吻合。
为了验证模型的有效性,此处采用了仿真与试验对比进行验证。以某8×4自卸车为试验对象,在C级公路上以70 km/h的速度行驶,测试车身座椅处垂直加速度,并将其测试结果与仿真结果对比如图5。可以看出其曲线变化趋势相似,验证了9自由度动力学模型是和实际吻合的。
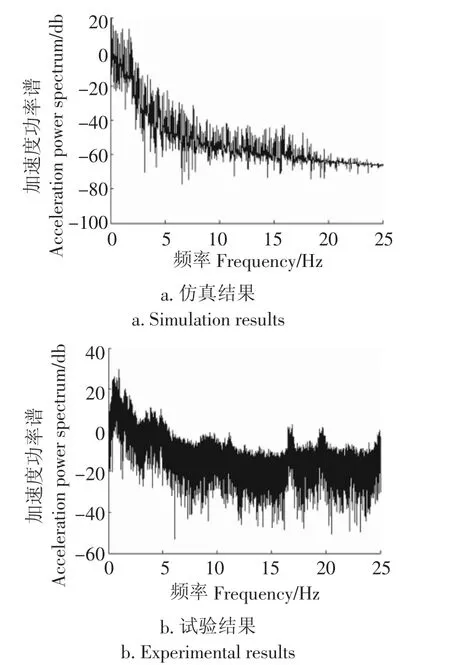
图5 70 km/h车身座椅加速度试验与仿真结果对比Fig.5 70 km/h body seat acceleration experiment compared with simulation results
3 基于人工鱼群算法的悬架参数优化
3.1 优化变量
双前桥的悬架参数对平顺性影响较大,选取前悬架刚度K3,K4阻尼C3,C4作为优化的设计变量,可表示为:

3.2 目标函数
驾驶舒适性指标中,主要以座椅垂向加速度值为主要参数,以减小其均方根值为优化目标,采用二次回归正交组合设计来建立目标函数。
依据二次回归正交组合设计原理,因素数P=4,二次回归模型的回归方程为[11]:
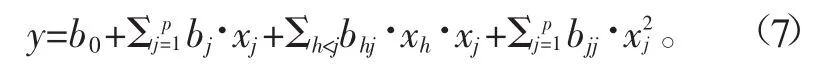
其中xh和xj是设计变量,bj是回归系数。通过逐步回归的方法可获得回归方程的回归系数,见表2。
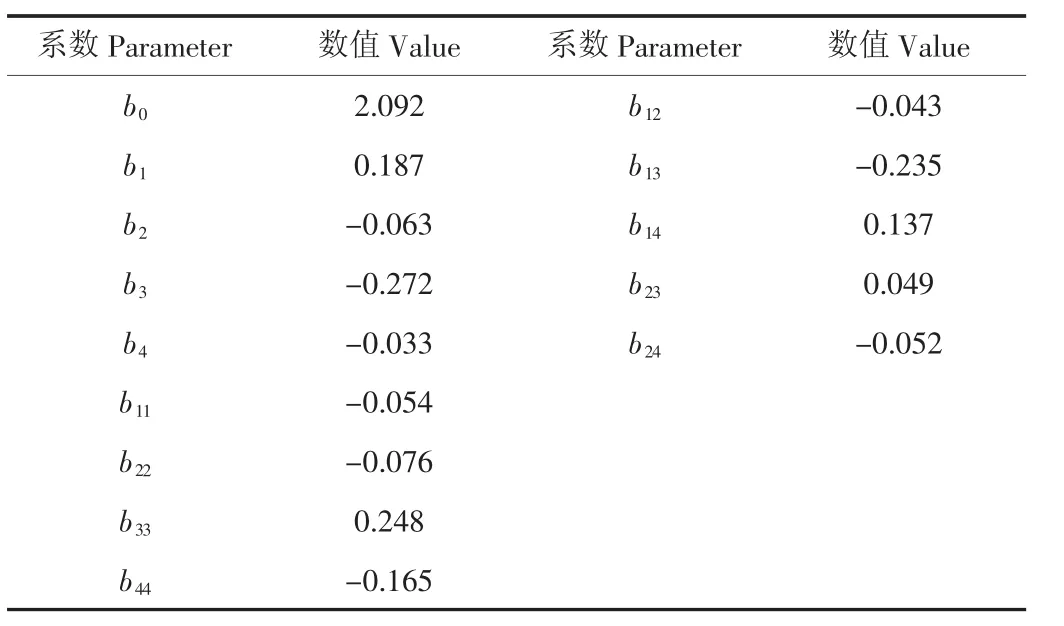
表2 回归系数表Tab.2 Regression coefficient table
3.3 人工鱼群智能优化算法
群(体)智能(swarm intelligence,SI)是指由简单的独立个体所组成的群体,能够协同工作自动搜索并找到最佳位置,体现出非常复杂的行为特征。由其延伸发展的优化算法是一类基于概率统计的随机搜索算法,目前有蚁群算法,粒子群算法(particle swarm optimization,PSO),蛙跳算法shuffled frog leaping algorithm,SFLA),人工鱼群算法(artificial fish swarm algorithm,AFSA)等[12]。近几年有的文献中提出了混合算法和多目标的优化,有混合蛙跳算法[13],Relief F和粒子群算法(particle swarm optimization,PSO)相结合的混合特征选择方法[14]。运用NSGA-Ⅱ遗传算法进行多目标优化分析[15],蜂群算法[16],粒子群和蜂群混合算法[17]。
人工鱼群算法是基于鱼群行为开发的行为主义人工智能算法。
通过模拟鱼的觅食、聚群、追尾等行为,设计了自下而上的寻优算法,其算法流程如图6所示。在食物浓度等引导下,通过觅食、聚群、追尾行为使得人工鱼最终聚集在几个局部极值点附近。
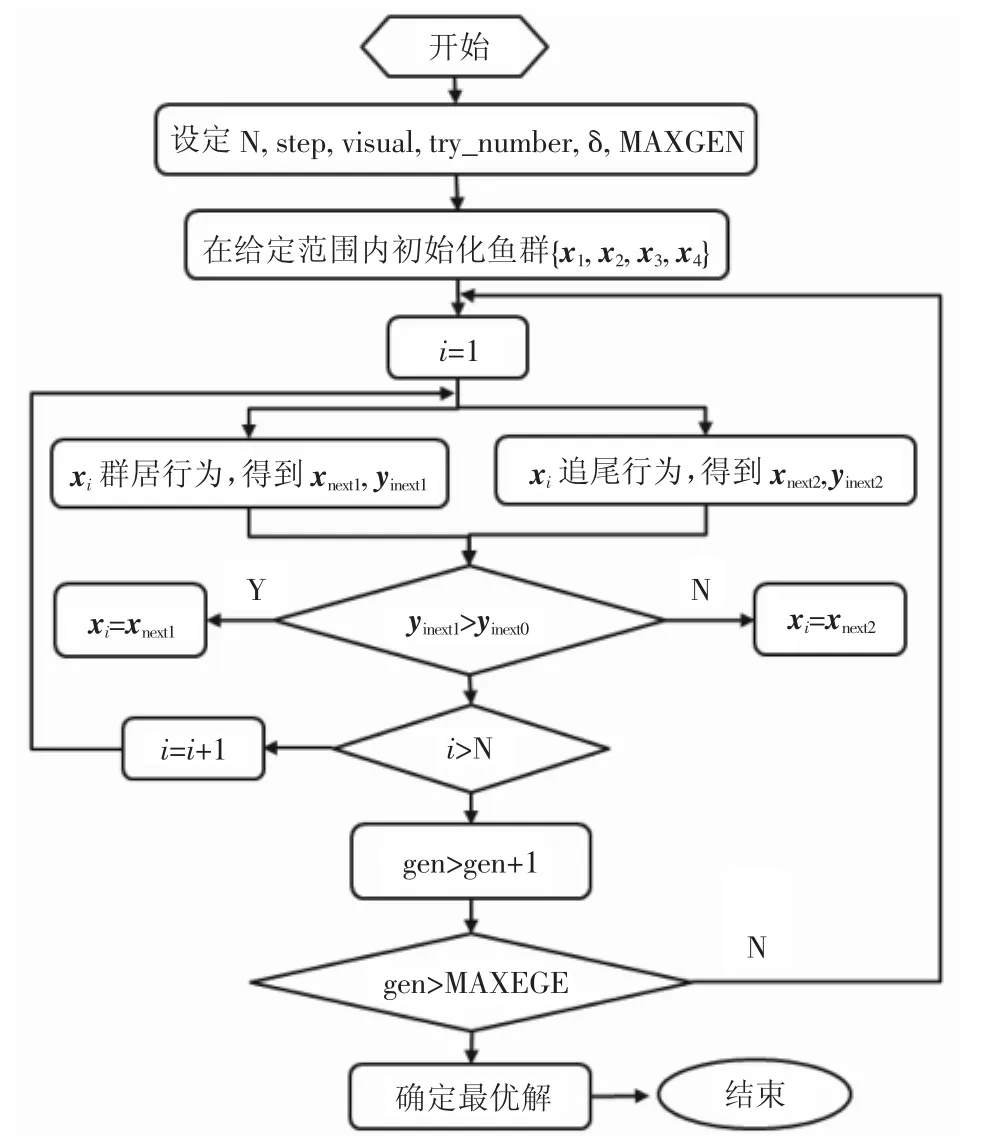
图6 人工鱼群算法流程图Fig.6 Artificial fish swarm algorithm flow chart
单个人工鱼个体当前的位置可以用向量X来表示,该向量中元素表示人工鱼寻求最优的控制变量;人工鱼当前所处位置则由食物浓度Yi表示,其表示最优目标函数值;dij=‖Xj-Xi‖则表示人工鱼个体之间的距离,就是向量的范数;拥挤度因子用δ表示;人工鱼自动的最大步长值用Step来表示;人工鱼个体可感知的距离用Visual来表示。人工鱼群算法在开始时对鱼群进行初始化,人工鱼个体通过觅食、聚群、追尾行为进行迭代更新目标函数值寻优,达到全局优化的目的。
1)鱼群初始化
在给定范围内产生随机数组,以任一组实数作为鱼群中的一条人工鱼。
2)觅食行为
假设人工鱼所在状态为Xi,在感知范围内选择任一状态Xj,对两种状态的食物浓度进行判断,若yi 式中,Xinext表示人工鱼个体下一步状态向量;rand()表示一随机数(0至Step)。 3)群居行为 群居行为通过领域内伙伴数目和食物浓度两个参数进行判断,人工鱼前进方向为食物较多和伙伴数目不多的方向。人工鱼当前状态为Xi,假设领域内伙伴数目为nf,且其中心位置Xc,如果Ycnf<δYi成立,则朝伙伴的中心位置方向前进,否则执行觅食行为。 4)追尾行为 人工鱼当前状态为Xi,假设领域内伙伴数目为nf,伙伴中Yj为最小的伙伴Xj,如果Yjnf<δYi成立,则伙伴Xj的有较高的食物浓度且周围不太拥挤,则朝伙伴Xj的位置方向前进,否则执行觅食行为。 5)随机行为 在执行这种行为时,是在其可以看见的视野范围内,随机选择一个位置,并向其游去,这种行为实际上是觅食行为的一种缺省值。 综上所述,人工鱼群算法通过食物浓度和中心位置处的伙伴数目来确定优化搜索方向,通过迭代搜索使人工鱼聚集在食物浓度密集处,达到全局优化的目的。 人工鱼群算法采用启发式的搜索策略,是一种广义领域的搜索算法,可采取串行或并行模式实现并且算法具备全局收敛能力,对初值选取和寻优函数无特殊要求,因此算法的参数设置范围较广,增强了算法的适应性和通用性。算法面向对象的实现方式能有效的结合实际问题,获得良好的应用效果。文献[18]应用实数编码遗传算法和人工鱼群算法的混合算法对短期电力系统优化调度,实现全局和局部搜索最优解。组合拍卖的赢家的决心问题是电子商务的热点问题,文献[19]应用混合鱼群算法来解决这一问题,试验结果显示这是一快速有效的优化算法。股票指数的预测在金融领域是一个热点问题,文献[20]建立了径向基函数神经网络来收集数据和预测股票指数,应用人工鱼群算法优化径向基函数。 经过多次试验,优化时鱼群算法采用的操作参数如下:种群数N为100,步长Step为100,感知距离Visual为20000,最大试探次数Try_number为100,拥挤度因子δ为9,最大迭代次数MAXGEN为50。 3.4 平顺性优化结果 平顺性优化分析属于组合优化问题,组合优化的对象则是解空间的中的离散状态。组合最优化的特点是可行解集合为有限点集,由直观可知,只要将定义域中有限个点逐一判别是否满足约束条件并比较目标值的大小,该问题的最优解一定存在并且可以得到。同时汽车平顺性的非线性导致悬架参数优化实质上是一个非线性多峰的优化问题,为了避免局部最优的现象和问题,采用带有随机性的进化算法是一个不错的选择,为此,使用人工鱼群智能算法来求解汽车平顺性优化问题。 本文在建立整车模型的基础上,将双前悬架刚度阻尼作为优化变量,以式(7)作为目标函数,借助人工鱼群智能算法,对双前桥悬架参数进行优化设计。 单个人工鱼个体当前的位置向量X={x1,x2,x3,…xn}对应需要优化的悬架参数设计变量X=[K3,K4,C3,C4]T,食物浓度Y表示优化目标车身座椅处垂直加速度值,种群数量N表示悬架参数X在取值范围内可能取值的数量,步长Step表示悬架参数每一次增加或减小的量,感知距离Visual表示每次寻优的变量范围。 优化后的悬架特性参数见表3。 表3 优化后悬架力学特性参数Tab.3 Optimized suspension mechanical characteristic parameters 优化前后不同速度时座椅垂直方向加速度均方根的对比见图7。可以看出,从10~120 km/h范围内,加速度均方根平均下降16.82%,在60 km/h时下降最大,加速度均方根下降21.24%,通过优化有效的提升了整车的平顺性。 图7 驾驶员座椅加速度优化前后对比Fig.7 Driver′s seat acceleration compared before and after optimization 1)本文建立9自由度的整车振动数学模型,运用Matlab平台编制了仿真程序,通过与试验结果对比,可知模型是有效可信的。 2)把人工鱼群智能优化算法应用到重型车平顺性分析中。鱼群算法是目前交叉学科中一个非常活跃的前沿性研究问题,通过优化,座椅垂直方向加速度方均根值在不同车速下均有所降低,从10~120 km/h范围内,加速度均方根平均下降16.82%,在60 km/h时下降最大,加速度均方根下降21.24%,有效提高了重型车的平顺性能。 [1]朱位宇.某重型卡车平顺性研究及悬架阻尼优化设计[D].长沙:湖南大学,2012. Zhu Weiyu.Ride Performance of Heavy Vehicle and the Suspension Damper Optimal Design[D].Changsha:Hunan University,2012.(in Chinese with English abstract.) [2]米承继,谷正气,伍文广,等.基于参数辨识的矿用自卸车平顺性优化[J].机械工程学报,2012,48(6):109-115. Mi Chengji,Gu Zhengqi,Wu Wenguang,et al.Mining dump truck ride optimization based on parameter identification[J]. Journal of Mechanical Engineering,2012,48(6):109-115.(in Chinese with English abstract.) [3] 催航.基于微粒群算法的汽车行驶平顺性参数优化[D].长春:吉林大学,2007. Cui Hang.Parameters Optimization of Car Ride Comfort Based on Particle Swarm Optimization[D].Changchun:Jilin University, 2007.(in Chinese with English abstract.) [4]李伟平,王磊,张宝珍,等.基于不确定性和模糊理论的汽车平顺性优化[J].机械科学与技术,2013,32(5):636-640. Li Weiping,Wang Lei,Zhang Baozhen,et al.Optimizing vehicle ride comfort based on uncertainty theory and fuzzy theory[J]. Mechanical Science and Technology for Aerospace Engineering, 2013,32(5):636-640.(in Chinese with English abstract) [5]Pedro J O,Dangor M,Dahunsi O A,et al.Intelligent feedback linearization control of nonlinear electro hydraulic suspension systems using particles warm optimization[J].Applied Soft Computing,2014,24:50-62. [6]Qazi A J,Farooqui U A,Khan A,et al.Optimization of semi-Active suspension system using particle swarm optimization algorithm[J].AASRI Procedia,2013,4:160-166. [7]徐中明,周小林,余烽,等.汽车平顺性分析中时域法和频域法的对比[J].汽车工程,2012,4(34):307-310. Xu Zhongming,Zhou Xiaolin,Yu Feng,et al.Comparison between time and frequency domain method in vehicle ride comfort analysis[J].Automotive Engineering,2012,4(34):307-310.(in Chinese with English abstract) [8]李晓磊.一种新型的智能优化方法一人工鱼群算法[D].杭州:浙江大学,2002. Li Xiaolei.A New Intelligent Optimization Method-Artificial Fish School Algorithm[D].Hangzhou:Zhejiang University,2002. (in Chinese with English abstract) [9]闻邦椿.机械振动理论及应用[M].刘树英,陈照波,等.北京:高等教育出版社,2009. [10]檀润华.路面对汽车激励的时域模型建立及计算机仿真[J].中国公路学报,1998,11(3):96-102. Tan Runhua.The mathematical models in time domain for the road disturbances and the simulation[J].China Journal of Highway and Transport,1998,11(3):96-102.(in Chinese with English abstract) [11]陈新志.基于稳健性的半挂汽车列车平顺性优化设计技术研究[D].太原:太原理工大学,2014. Chen Xinzhi.Robust Optimization Design for Ride Comfort of Articulated Vehicle[D].Taiyuan:Taiyuan University of Technology, 2014.(in Chinese with English abstract) [12]王联国.人工鱼群算法及其应用研究[D].兰州:兰州理工大学,2009. Wang Lianguo.The Research of Artificial Fish Swarm Algorithm anditsApplication[D].Lanzhou:LanzhouUniversityofTechnology, 2009.(in Chinese with English abstract) [13]郭小燕,刘学录,王联国,等.基于混合蛙跳算法的土地利用格局优化[J].农业工程学报,2015,31(24),281-288. Guo Xiaoyan,Liu Xuelu,Wang Lianguo,et al.Land use pattern optimization based on shuffled frog leaping algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2015,31(24),281-288.(in Chinese with English abstract) [14]肖艳,姜琦刚,王斌,等.基于Relief F和PSO混合特征选择的面向对象土地利用分类[J].农业工程学报,2016,32(4):211-216. Xiao Yan,Jiang Qigang,Wang Bin,et al.Object based land-use classification based on hybrid feature selection method of combining Relief F and PSO[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2016,32(4):211-216.(in Chinese with English abstract.) [15]王春林,叶剑,曾成,等.基于NSGA-Ⅱ遗传算法高比转速混流泵多目标优化设计[J].农业工程学报,2015,31(18),100-106. Wang Chunlin,Ye Jian,Zeng Cheng,et al.Multi-objective optimum design of high specific speed mixed-flow pump based on NSGA-Ⅱgenetic algorithm[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015,31(18),100-106.(in Chinese with English abstract) [16]徐龙琴,李乾川,刘双印,等.基于集合经验模态分解和人工蜂群算法的工厂化养殖pH值预测[J].农业工程学报,2016,32(3):202-209. Xu Longqin,Li Qianchuan,Liu Shuangyin,et al.Prediction of pH value in industrialized aquaculture based on ensemble empirical mode decomposition and improved artificial bee colony algorithm[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2016,32 (3):202-209.(in Chinese with English abstract) [17]陈述,邵东国,李浩鑫,等.基于粒子群人工蜂群算法的灌区渠-塘-田优化调配耦合模型[J].农业工程学报,2014,30 (20):90-97. Chen Shu,Shao Dongguo,Li Haoxin,et al.Coupled allocation model for optimizing water in canal-pond-field based on artificial bee colony and particle swarm algorithm[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2014,30(20):90-97.(in Chinese with English abstract) [18]Na Fang,Jianzhong Zhou,Rui Zhang,et al.A hybrid of real coded genetic algorithm and artificial fish swarm algorithm forshort-term optimal hydrothermal scheduling[J].Electrical Power and Energy Systems,2014,62:617-629. [19]Genrang Zhenga,Zheng Chun Linb.A winner determination algorithm for combinatorial auctions based on hybrid artificial fish swarm algorithm[J].Physics Procedia,2012,25:1666-1670. [20]Wei Shen,Xiaopen Guo,Chao Wu,et al.Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm[J].Knowledge-Based Systems, 2011,24:378-385. Vehicle ride comfort analysis and optimization based on artificial fish swarm algorithm Fan Zhengwu,Wang Tie,Chen Zhi Ride comfort is of great importance feature for the heavy truck,its optimization can improve the driver's driving conditions to reduce fatigue,and make the goods safer.Primary factors that can influence ride comfort are form and parameters of suspension,which are suspension stiffness,suspension damp and their combination.When the form of suspension is confirmed,more reasonable parameters can be selected by optimization method to improve ride comfort.Ride comfort optimization analysis belongs to the combinatorial optimization problem,at the same time,the nonlinear characteristics in optimization is essentially a nonlinear multimodal optimization problem.In this paper,at first,a ninedegree of freedom vehicle vibration model was established;Vehicle driver seat acceleration simulation tests were conducted with different vehicle speed.Also,both time and frequency domain analysis was implemented with MATLAB software development platform.On the whole,with the increase of the speed of the vehicle,the acceleration root-mean-square of vehicle driver seat became larger,so the vehicle ride comfort performance reduced.Especially at low speed and high acceleration change is more obvious.But in 40~80 km/h,the acceleration change quite gentle.That means to achieve the better economy and the vehicle ride comfort performance,the vehicle speed keeping in a medium speed is better.Based on C level road and the speed of 70 km/h,with an eight by four dump truck as experimental object,the ride comfort tests were conducted,moreover the test results compared with the results of simulation.The compared results showed that the simulation and the test were very close.And then,today technology was coming to a stage of intersection,infiltration,and interaction with multi-subjects.More and more issues on complexity,non-linearity,and system have come to us.To deal with such complexity of system,conventional techniques have become incapable,and to seek an optimization algorithm, which adapt to large-scale parallel with intelligent characteristics,has been a primary research target of related subjects. The artificial fish algorithm was proposed to optimize ride comfort.The artificial fish swarm algorithm (AFSA),a new method based on animal behaviors and the typical application of behaviorism artificial intelligence,was proposed by an internal scholar in recent years.It used the operators such as prey,swarm,follow and random behavior.The algorithm parameters,such as population,step size,sense of distance,the largest try-number,crowded degree coefficient and the largest number of iterations,has a great impact on the performance of the convergence.At the end,the artificial fish algorithm was used to optimize ride comfort by reasonable selection of the suspension parameters.The objective function was the acceleration root-mean-square of vehicle driver seat to be minimized.The decision variables were front suspension stiffness and damp.Moreover AFSA need to set up the appropriate algorithm parameters.For example,population scale, step size,sense of distance,the largest try-number,crowded degree coefficient and the largest number of iterations was 100, 100,20 000,100,9 and 50.Where the population scale N was called the number of possible values of suspension parameters within the value range,step size was suspension parameters increasing or decreasing the amount of each iteration,and sense of distance visual was variables scope of each iteration.Optimization results show that the acceleration root-mean-square average fell by 16.82%,the biggest fell by 21.24%in 60 km/h,so it effectively improves the ride comfort h performance of heavy vehicles. ariculturel machinery;models;optimization;comfort;optimization analysis;artificial fish algorithm;application 10.11975/j.issn.1002-6819.2016.06.015 U461.4 A 1002-6819(2016)-06-0107-08 2015-09-12 2016-01-25 山西省高新技术产业化项目(2011-2368);太原理工大学校基金团队项目(2014TD033) 范政武(1976-),男(汉),博士生,主要研究方向是车辆现代设计理论与方法。太原市迎泽西大街79号太原理工大学齿轮研究所030024。Email:fanzhengwu2008@126.com ※通信作者:王 铁(1957-),男(汉),博士、教授。中国机械工程学会高级会员/失效分析专家、全国齿轮标准化技术委员会委员、山西省机械工程学会常务理事兼副秘书长。博士研究生导师,主要研究方向是汽车现代设计与汽车动力学。太原市迎泽西大街79号太原理工大学齿轮研究所030024。Email:wangtie57@163.com
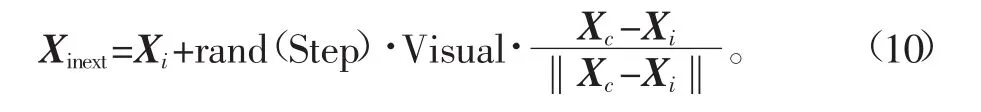
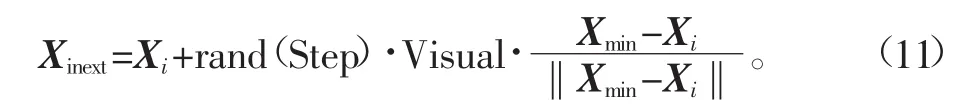
4 结论
(Department of Vehicle Engineering,Taiyuan University of Technology,Taiyuan 030024,China)
