傅氏算法在电力系统继电保护中的应用研究

2016-05-17广东电网有限责任公司湛江供电局

电子世界 2016年8期

关键词：应用

广东电网有限责任公司湛江供电局陈婷

傅氏算法在电力系统继电保护中的应用研究

广东电网有限责任公司湛江供电局陈婷

【摘要】随着经济的快速发展和人们生活水平的不断提升，人们生产生活对电力系统稳定性和可靠性的依赖性逐渐增强，所以电力系统继电保护越来越受到关注，本文为对电力系统继电保护产生更加全面的认识，推动其整体水平的提升，将傅氏算法应用于电力系统继电保护中，通过对傅氏算法基本原理、电力系统继电保护中的傅氏算法进行系统研究，结合实例对傅氏算法在电力系统继电保护中应用的作用展开探讨。

【关键词】傅氏算法；电力系统继电保护；应用

1　前言

电力系统在发生故障后，受故障电压、电流中的暂态噪声影响，通过对故障电压、电流基波相量或二者的组合进行故障判断的难度较大，而傅氏算法凭借其算法的简便性和性能的优越性，成为利用滤波算法滤除干扰噪声的主要手段，所以对傅氏算法在电力系统继电保护中的应用展开研究具有重要的现实意义。

2　傅氏算法基本原理

傅氏算法属于以周期函数为对象的算法，将周期信号分为成不同的傅氏级数，换言之将周期信号分为成正弦函数与余弦函数的和，通常情况下周期为T的信号f(t)傅里叶级数可以表示为：

由此可见f(t)的n次谐波分量及可以表示为：

所以在电力系统中如果故障信号属于周期信号x(t)，那么整个周期信号中就会涵盖基波、衰减的直流分量以及各次谐波分量，所以如果用xi表示其在第i此谐波分量的幅值；φi表示其在第i此谐波分量的初相角；xsi表示其在第i此谐波分解后得到的正弦分量幅值；xci表示其在第i此谐波分解后得到的余弦分量幅值；A表示衰减分量的初始值；a表示衰减分量的衰减常数，其整体就可以表示为：

也可以表示为：

3　电力系统继电保护中的傅氏算法分析

现阶段傅氏算法在电力系统继电保护中非常常见，其可以对高次谐波进行有效的消除，直接将工频分量从采样数据中提取，为继电保护装置运行状态的调整提供依据，现阶段应用于电力系统继电保护中的傅氏算法包括全波傅氏算法、半波傅氏算法和诸多两者改进算法[3]。

3.1全波傅氏算法

如果电力系统中的输入信号x(t)可以表示为：

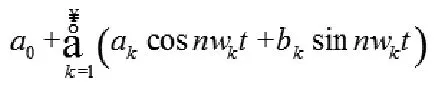
将其第i次谐波分量的实体部分Xci表示为：

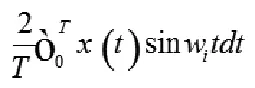
此时结合三角函数自身含有的正交性，可以确定i=k，所以第i次谐波分量的实体部分Xci就可以直接表示为，而此时第i此谐波分解后得到的正弦分量幅值Xsi就可以直接表示为，其也可以视为第i次谐波分量的虚体部分，如果将信号中第i次谐波分量的幅值ai表示为，那么信号的全波傅氏算法就可以表示为：

通过以上三个公式可以实现对信号中所有整次谐波分量、直流分量和n次谐波分量的过滤消除，而且实践证明整个消除过程稳定持续，但其以周期作为计算的划分，而且以采样信号不含衰减直流分量推导为基础，所以此算法针对直流分量的滤出效果相对较不明显，在应用的过程中应结合实际情况选择[4]。

3.2半波傅氏算法

半波傅氏算法建立在全波傅氏算法的基础上，是半个周波作为其积分区间，换言之在半波傅氏算法中，其：

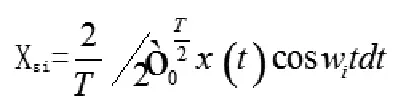
可见半波傅氏算法可以对电力系统中的直流分量和次谐波分量直接消除，仅留下基波分量，通过半波傅氏算法与全波傅氏算法在电力系统继电保护中的应用对比分析可以发现，半波傅氏算法仅通过半个周期的采样数据即可以达到对故障的判断目的，效率得到明显的提升，但其消除滤波的能力相比全波傅氏算法也呈现出明显的缩减趋势，对偶次谐波的消除功能明显被淡化，看见两者相互存在各自的优缺点，在电力系统中的应用要结合实际情况在两者中择优应用。

3.3诸多两者改进算法

所谓傅氏级数即以输入信号作为理想周期信号的基础，但在实际电力系统中信号并不能均为理想信号，所以在实际的傅氏算法中与理论上的傅氏算法存在较大的区别，而对两种算法进行改进的离散傅氏变换避免了信号的干扰，在计算的过程中并不需要处理信号对其产生直接作用，所以在电力系统继电保护的实际计算的过程中，通常将半波傅氏算法与全波傅氏算法都用离散形式表示，如果将每个周波内等间隔的采样点数设定为N，则可以将全波傅氏算法表示为：

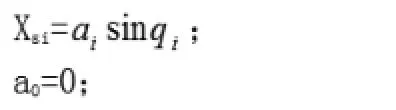
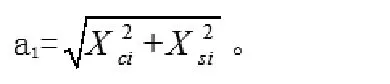
半波傅氏算法表示为：由于这种离散形式与电力系统中故障判断实际情况更为接近，所以次计算方式在电力系统继电保护计算中的应用更为常见，除此种形式的优化外，现阶段大量专家学者对其进行进一步的优化设计，其优化空间仍相对广泛，此方面我国研究相对西方发达国家存在滞后现象，所以在加大探索力度的同时，应积极借鉴西方发达国家的成功经验。

4　结合实例分析傅氏算法在电力系统继电保护中应用的作用

如果某输入信号的衰减分量的衰减常数为10，整体可以表示为10+45.76sin(100∏t+66.520)+3.65cos(300∏-24.120)，那么利用半波傅氏算法与全波傅氏算法的离散形式对其进行计算，进行三次采样，第一次采样为12点，第二次采样为16点，第三次采样为20点，通过半波傅氏算法与全波傅氏算法的离散形式计算结果可以发现，当采集的点数逐渐上升的同时，傅氏算法提取的基波和三次谐波的幅值、相位角等数据与电力系统的真实值的相符程度越高，其中基波和三次谐波的幅值最为明显，再次计算的过程中仍存在直流分量对判断故障的过程产生干扰，但判断结果的准确率已经可以满足实际要求，如果在此基础上将采点的数量进一步提升，使之达到几百甚至更大，判断的准确性将更加有保证，可见此计算方法在电力系统继电保护中应用对提升继电保护的安全性和可靠性具有重要的意义，但在采样的过程中需要注意，虽然采集点数的提升对判断准确性更加有保证，但其对判断的效率会产生影响，进而增加判断的成本要对两者进行综合分析，从此角度分析可以发现半波傅氏算法实质上是全波傅氏算法在速度上的一种改进。另外，通过案例中半波傅氏算法与全波傅氏算法计算过程和结果的纵向对比分析可以发现，全波傅氏算法的滤波效果更加理想，其几乎可以对所有整次谐波进行有效的过滤，而且在计算的过程中多获取的基波和三次谐波幅值和相位角等与实际情况的相符程度更高，但其在速度方面相半波傅氏算法存在一个数据窗的时延，使其应用的范围和效果受到较严重的制约，这是全波傅氏算法现阶段在推广应用方面受到限制的主要原因，通过实践计算，对两种傅氏算法在电力系统继电保护中应用的不同效果进行了进一步的证明，在实践应用的过程中要结合实际情况选择。