个人信用评估组合模型选择方案研究

任　潇, 姜明辉 , 车　凯, 王　尚

(1.哈尔滨工业大学 经济与管理学院，150001 哈尔滨； 2.哈尔滨工业大学 计算机科学与技术学院，150001 哈尔滨；3.哈尔滨工业大学 材料科学与工程学院，150001 哈尔滨)



个人信用评估组合模型选择方案研究

任潇1, 姜明辉1, 车凯2, 王尚3

(1.哈尔滨工业大学 经济与管理学院，150001 哈尔滨； 2.哈尔滨工业大学 计算机科学与技术学院，150001 哈尔滨；3.哈尔滨工业大学 材料科学与工程学院，150001 哈尔滨)

摘要:为准确评估借款人的信用和合理控制商业银行风险,首先对个人信用评分模型的常用模型进行了总结和归纳，然后通过分析比较说明了不同模型的准确性. 在“坏样本”的区分与结果判断上采用加权方式，提出修正算法来确定信用评分模型中的指标权重，满足不同银行数据多样化的需要，提高评分模型精度.

关键词:风险控制；个人信用；信用评分模型；修正算法

目前，我国的个人信用评估体系还处于发展阶段，信用制度不够健全，各大银行在信用评估过程中更多采用基于经验主义的判断方法，国内学者的研究大多数都是偏向于评分指标体系的理论性研究[1].

Logistic回归方法以其强大的稳健性和泛化能力被较多地应用到评估方法中[2]；神经网络对不完全信息具有很强的处理能力，能够解决现实生活中的非线性问题，而且分类精度非常高，也是优先选择的信用评估方法[3-4]；支持向量机能处理小样本、高维度的数据，并且获得较高的分类精度，对处于发展阶段的信用评估系统也是一个不错的选择[5-6].

总的来说评价指标体系被分为两大类[7]:体现还款能力的指标和体现还款意愿的指标. 这些指标相对较容易获得，并且能在一定程度上反映个人的真实还款能力和还款意愿,但是这些指标比较片面，容易出现误判，而且门槛非常高. 现阶段的专家投标法，模型主要的作用是对数据样本进行客观评估，但在评估模型中总是存在一些“坏样本”，如重点评估指标与总体一致，但一些次要的指标偏离了总体；有的样本本身信誉度没有问题，但重点指标又与评价结果不符；还有的样本自身的指标相互间存在矛盾. 为此，本文基于4种常用的统计学模型，设计了一种修正算法，同时考虑样本多样性以及影响因素之间的相关性问题，对信用评分的指标体系进行重新组合与打分加权，在保留统计学方法优点的基础上，进一步提高统计学模型的解释性及精确度，从而减少“坏样本”对模型评分结果的影响.

1评分模型

近年来随着信用评分研究的不断深入，神经网络以其较高的精确度得到了广泛的运用[4，8]. 但是，神经网络就像一个黑箱子，其解释性不强，不能体现不同变量的重要性. 而且，神经网络稳定性也不如其他统计学模型，在信用评分领域的应用也存在着严重的局限. 因此本文以回归模型、支持向量机模型和贝叶斯分类器模型为基础，使用加权法找出显著因子，确定影响评分结果的重点指标，并对数据结果进行交叉验证，从而得到一个修正的评价模型.

1.1回归分析模型

回归分析法是指在大量已知数据的基础上，探究一种变量(自变量)对另外一种变量(因变量)的影响，并建立能描述二者间相关关系的回归方程，在这一方程的基础上，根据已知自变量的值对因变量的值进行预测[9]. 在回归分析法中，应用最为广泛的是Logistic回归分析、Probit回归分析及多元线性回归. 在此，以Logistic回归分析为例进行说明.

设x1,x2,…,xn为与客户信用相关的n个特征值，y是客户的信用情况，是取值为0或1的随机变量. 假设样本集中有m个客户，即(xi1,xi2,…,xin; yi)(i=1,2,…，n)，则认为yi与xi1,xi2,…,xin满足以下的关系：

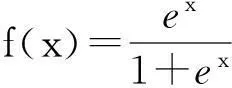
则Logisitc回归方程为

对以上方程做线性变化，即可得

尽管在个人信用评分的实践中，回归分析的鲁棒性低于判别分析，但回归分析对数据分布的要求相对宽松，而且能够提供客户的违约概率，因此获得了大多数学者和银行业的青睐. 目前为止，Logistic回归已经成为所有回归方法中最成功、最常用的统计方法之一.

1.2支持向量机模型

支持向量机的基本思想是将输入空间的样本通过非线性变换映射到高维特征空间，然后在特征空间中求取把样本线性分开的最优分类面[10]. 这一模型针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能.

设训练样本集D={(xi, yi}(i =1 , 2 , …, m) , xi∈ Rn, yi∈(+1 , -1)}, yi为输出. 把这m 个样本点看作是n维空间中的点, 如果存在一个分类超平面

这个超平面能将m个样本分为两类，而且能使分类间隔(2/‖w‖2)最大，这样的超平面称为最优分类面. 要使分类间隔最大就等价于使‖w‖2/2 最小，寻求最优分类面的问题就转化为求解下面的最优化问题：

(1)

根据优化理论, 可得线性可分条件下的分类决策树为

式中：b*是分类阈值；αi是每个样本对应的Lagrange乘子，αi不为零时所对应的样本就是支持向量. 对于线性不可分情况，通常要引进核函数来解决. 只要采用的内积核函数适当，就可以将低维输入空间中的非线性可分问题转化为高维特征空间中的线性可分问题. 应注意的一点是，引入的核函数k应满Mercer′s条件. 此时需要在目标函数式中增加松弛变量ξi和惩罚函数C，式(1)转化为

所得分类决策函数为

1.3贝叶斯分类器

贝叶斯分类器的分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类. 也就是说，贝叶斯分类器是最小错误率意义上的优化. 用于分类的贝叶斯网络中应包含类结点C，其中C的取值来自于类集合(c1,c2,…,cm)，还包含一组结点X=(X1,X2,…,Xn)，表示用于分类的特征. 对于贝叶斯网络分类器，若某一待分类的样本D，其分类特征值为x= (x1,x2,…,xn) ，则样本D属于类别ci的概率P(C=ci|X1=x1,X2=x2,…,Xn=xn) (i=1, 2,…,m) 应满足下式：

P(C=ci|X=x)=Max{P(C=c1|X=x) ,

P(C=c2|X=x),…,P(C=cm|X=x)}.

而由贝叶斯公式

其中，P(C=ci) 可由领域专家的经验得到,而P(X=x|C=ci) 和P(X=x) 的计算则较困难. 对此贝叶斯估计一般采用两阶段选择方法：

第一阶段是贝叶斯网络分类器的学习，即从样本数据中构造分类器，包括结构学习和CPT学习；

第二阶段是贝叶斯网络分类器的推理，即计算类结点的条件概率，对分类数据进行分类.

这两个阶段的时间复杂性均取决于特征值间的依赖程度，甚至可以是NP完全问题，因而在实际应用中往往需要对贝叶斯网络分类器进行简化. 根据对特征值间不同关联程度的假设，可以得出各种贝叶斯分类器，NaiveBayes、TAN、BAN、GBN就是其中较典型、研究较深入的贝叶斯分类器.

2样本数据

为了保证预测模型的准确性，本文在建模时使用了银行的真实数据，但为了保护用户隐私，没有列出姓名，只是提取了打分所需的项目. 评估所用数据如表1所示，数据共4 500组，所有数据采用随机挑选方式分成训练组与验证组. 为保证建模准确性，每组数据中最终评分通过与不通过的比例均与原始数据一致，为3.5∶1.0.

3实验过程

在使用样本数据进行建模之前，先要对数据进行预处理. 对收集的数据采用Z-SCORE方法进行标准化处理，用公式可以表示为

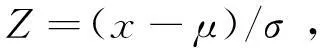
其中x为原数据，μ为平均数，σ为标准差.Z值反映出了原始数据与数据整体平均值之间的距离(以标准差为单位衡量)，适合样本中有离群数据的情况，标准化后的数据也可用来识别异常值.

由此可见，对意义的正确理解，是口译的核心，译员的知识储备、心理素质等多方面原因会影响其对意义的理解。按释意理论重意义的模式，从各方面研究对意义的理解，以辅助译员正确理解意义，确实是口译研究的一个重要方向。

3.1Logistic回归分析

采用SPS软件进行Logistic回归分析，分析结果如表2中所示.

由B 与显著性可以看出,职业和贷款期限是有显著影响的，这也符合信用风险评价的一般规律. 对于Logistic回归分析影响因素是否有效除了与其绝对数值大小，还与显著性上限Zmax有关. 一般而言，z<0.05时影响因素才有意义. 从表2中可以发现，符合这一条件的变量分别为有无配偶、贷款金额、受教育程度、担保方式以及月收入.

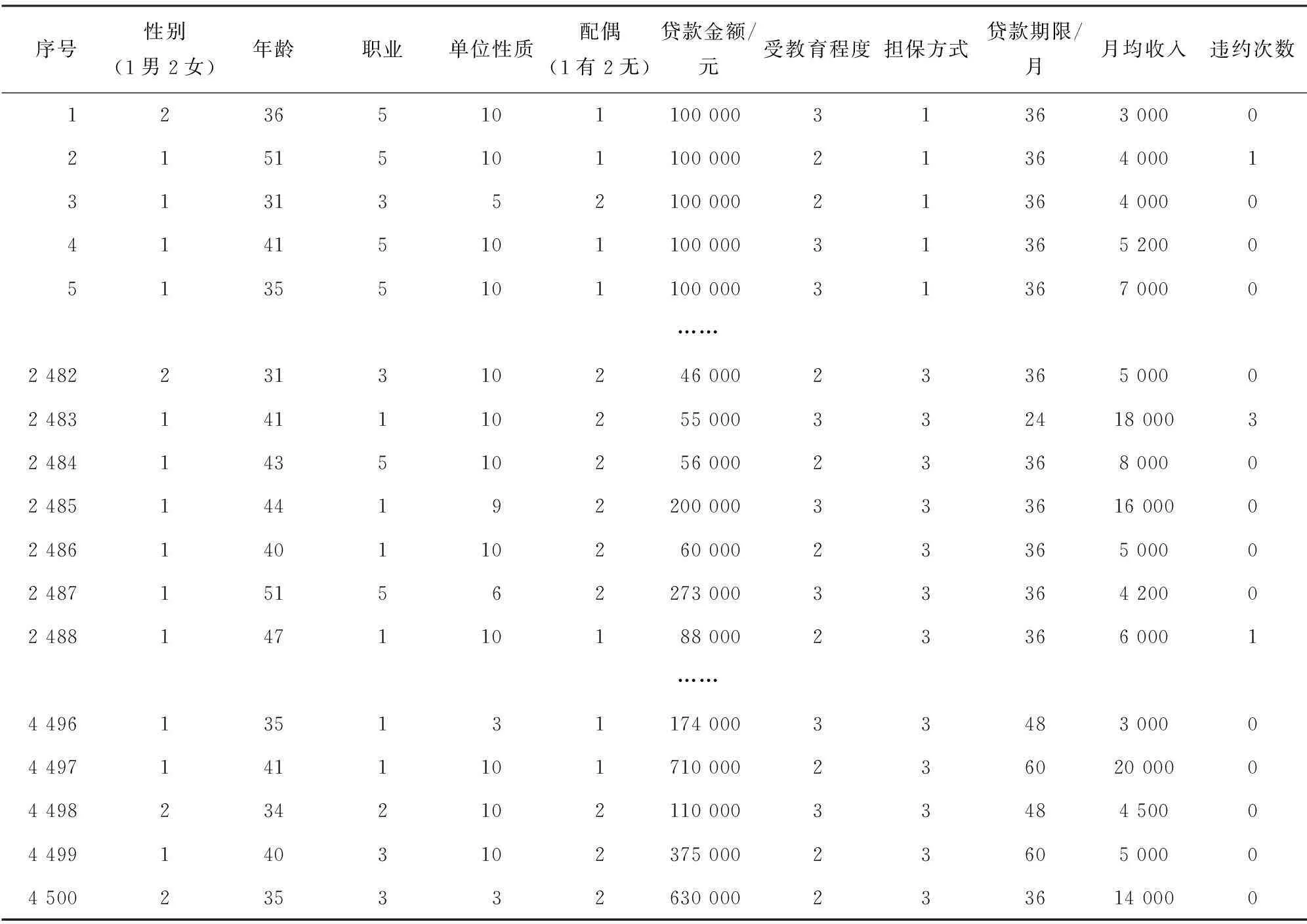
表1　来自银行的部分数据

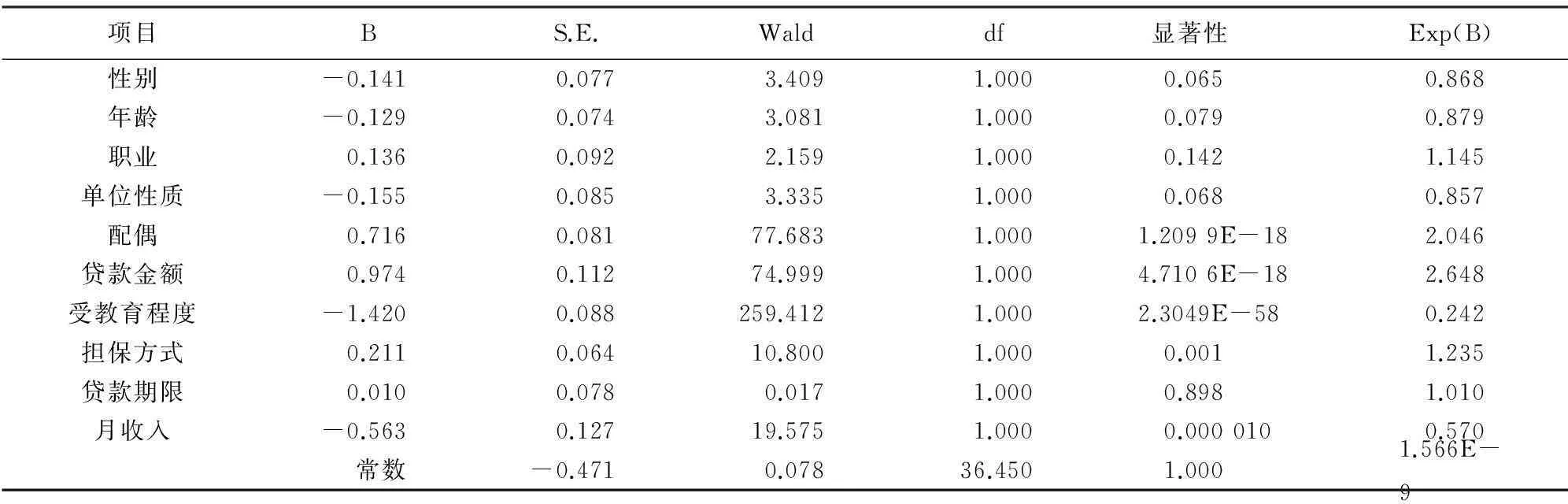
表2　Logistic回归分析结果

数据结果准确性分析如表3所示. 通过表3可以看出，相比于训练集较高的准确率，测试集的准确率偏低一些. 这一点可能是因为模型数据是依据训练集给出的，同时测试集的数据更多，也会影响精度，说明这一模型对数据的依赖程度较大.

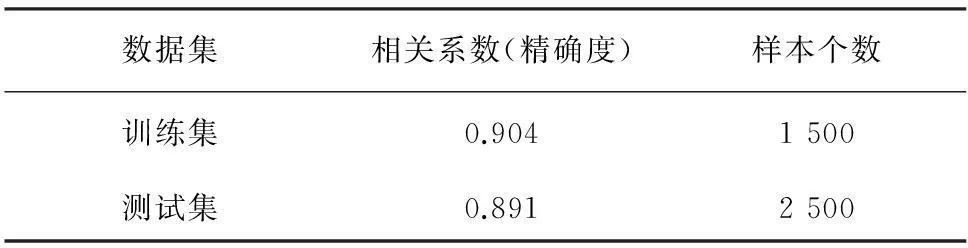
表3　数据结果准确性分析

3.2Probit回归分析

采用stata对数据进行Probit分析，其结果如表4所示. 其中在P>|z|一列中，0.000的数值表示远小于0.05的值，这一部分数据均为关键因素.

通过结果分析，发现数据的显著性排序基本与Logistic回归分析结果相同，但是也有一些不同. 除了有无配偶、贷款金额、受教育程度、担保方式以及月收入是关键因素以外，性别和年龄也会影响分析结果，这些差异也导致了这一模型误差较大. 数据结果准确性分析如表5所示.

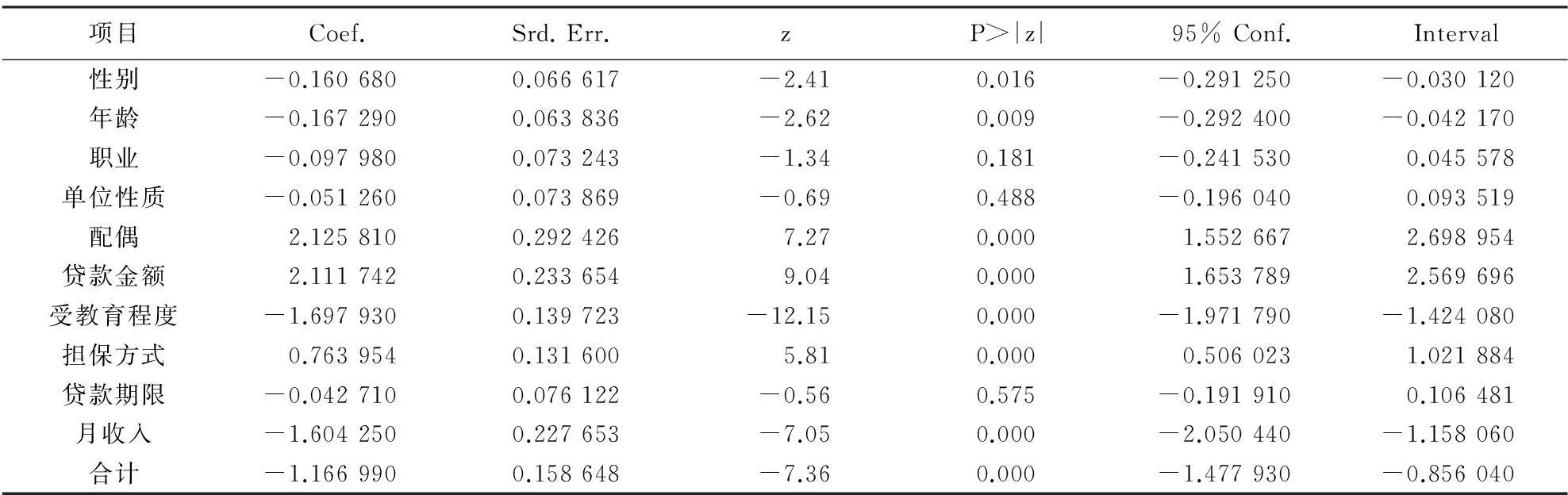
表4　Probit回归分析结果

表5　数据结果准确性分析

采用matlab对数据进行SVM分析，分析过程如图1所示. 在初次粗略计算后，SVM所得结果准确性较差，因此利用libsvm 工具包建立支持向量机模型之前，需对模型主要参数(惩罚系数c 和核函数中g)进行人为赋值，而这些参数是由训练样本的数值特性和模型所建立的规律来确定的，每个模型的c,g值都可能不同. 为了保证选取合适的参数值，具体优化方法为：选取一个足够宽的寻优范围，让c,g 按照一定的步长来迭代，利用每次迭代的参数值训练模型，通过交叉验证(K-CV 法)得到训练后的误差值，最终选取使得训练误差最小的c,g值作为最佳参数组合，并以此训练模型.

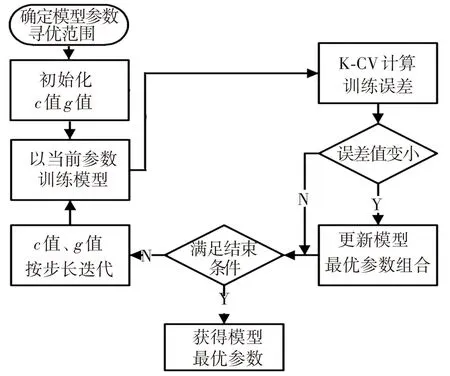
图1　SVM参数寻优基本流程

SVM参数寻优基本流程如图2所示. 由图2可知，随着等高线依次降低，MSE 值逐渐降低，经过c, g 的参数寻优，当模型训练MSE值为最小等高线在空间上为最低点时，c,g的组合值为最优取值. 本次参数寻优后，最佳c值为32，g值为0.062 5.

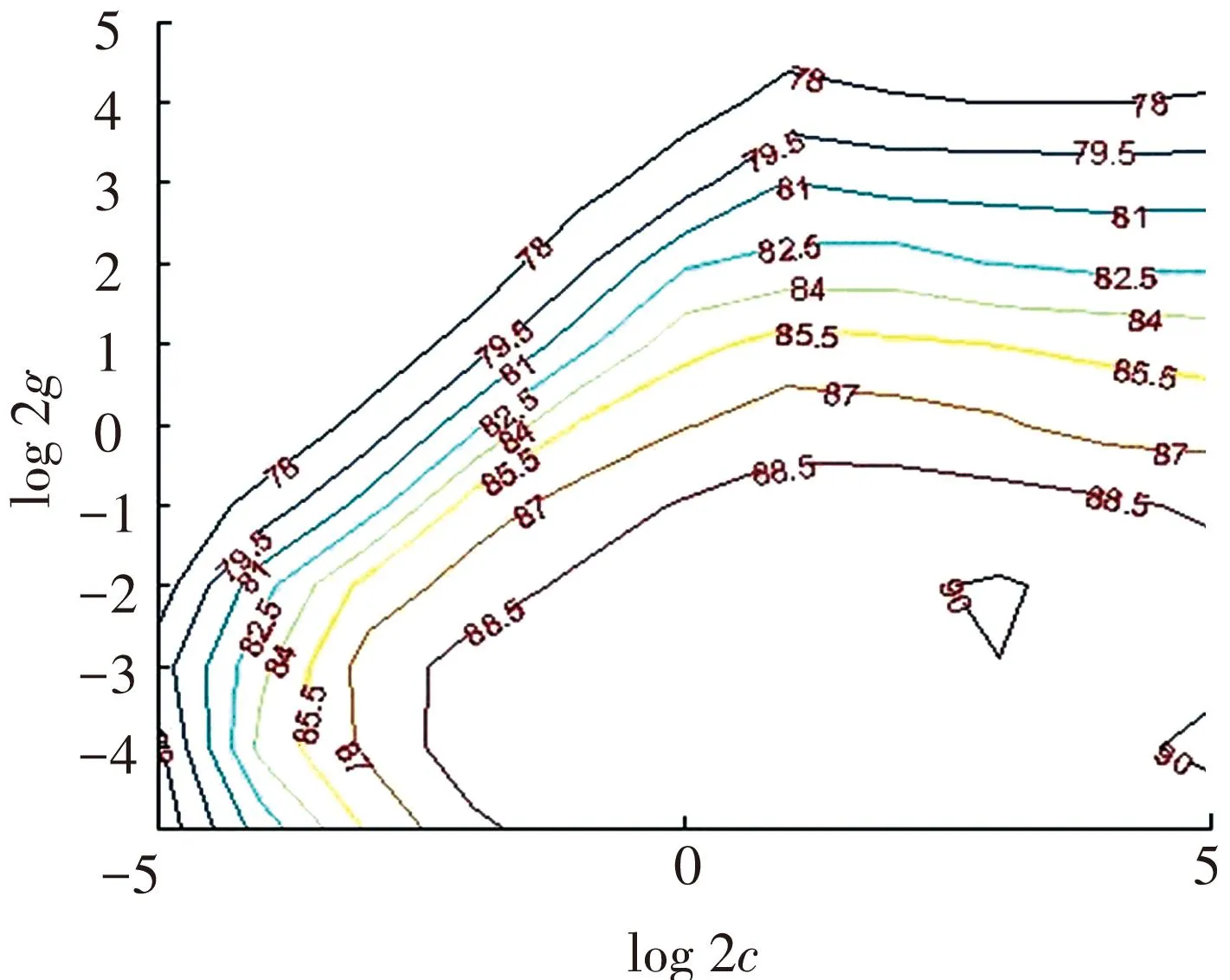
图2　SVM参数优化等高线

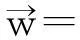
其中b=-2.100 1.

数据结果准确性分析如表6所示. 通过表6可以看出，相比于训练集较高的准确率，测试集的准确率偏低一些. 同之前分析一样，大样本下一些“坏样本”对结果造成了一定影响，所占权重较大的因素由大到小分别为：贷款额业、担保方式、配偶和职业. 这一结果也符合之前其他模型分析结果的规律，但即便如此，SVM方法的精确度依然高于其他分析方法.

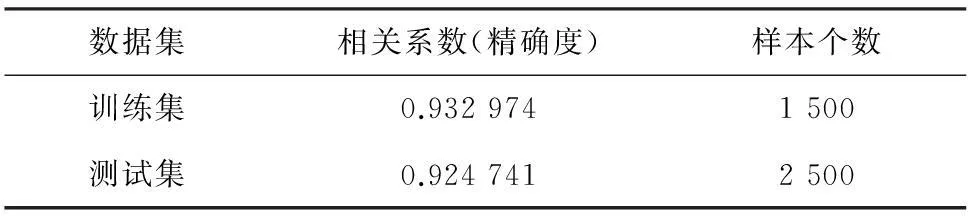
表6　数据结果准确性分析

3.4贝叶斯分类器

作为对比模型，朴素贝叶斯模型的构造采用matlab中内建的数据包对样本进行贝叶斯分析，默认数据服从高斯分布，且先验概率等于经验概率，得出的分类矩阵为

从分类矩阵可以得出，预测的准确率为0.867 3. 这一方法最为简单，求解速度最快，但相比于其他方法其准确度较低(如表7所示). 而且不能给出相关因素的显著性，如同神经网络一样，只能在“黑箱”中进行.

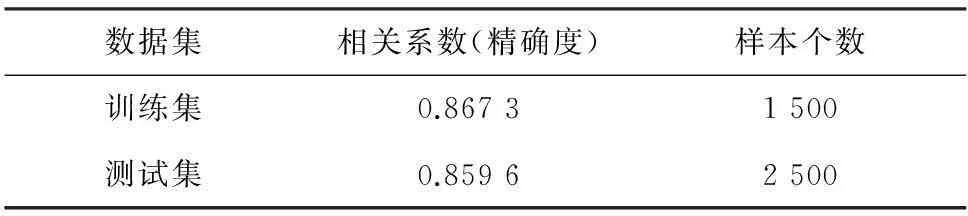
表7　数据结果准确性分析

通过比较训练组和验证组的数据，发现SVM的结果准确率最高，接下来是Logistic回归分析和Probit回归分析，最后是贝叶斯分析. 因此进一步对SVM方法进行优化，加入模型修正系数后，模型准确率有所提升，并且得到的向量平面能都直接反映出不同影响因素的权重. 因此，对于该银行数据的拟合结果说明，SVM模型能够进行快速分析并保证一定的准确性，并确定贷款额业、担保方式、配偶和职业为主要因素.

4结语

本文例举了4种常用的个人信用单一评分模型及组合评分模型，指出了模型的优缺点，并针对个人信用评分模型在我国的应用中出现的问题进行了分析探讨，发现SVM方法效果最好. 在此基础上，结合模型的应用实际，针对不同地区银行不同的业务样本数据，形成相应的指标体系，并对参数显著性进行了初步的排序，确定了几个对评估有重要意义的参数.在接下来的工作中将进一步对影响因素进一步筛选，并对SVM预测模型进行优化，达到更好的预测效果.

参考文献

[1] 朱晓明，刘治国.信用评分模型综述[J]. 统计与决策, 2007(2)：103-105.

[2] 姜明辉,姜磊,王雅林. 线性判别式分析在个人信用评估中的应用[J]. 管理科学,2003,16(1):53-55.

[3] 蓝润荣, 程希俊. 基于改进 RBF 神经网络的银行个人信用评级[J]. 中国科学院研究生院学报, 2013,30(3): 298-303.

[4] 朱兴德,冯铁军. 基于GA神经网络的个人信用评估[J]. 系统工程理论与实践,2003,23(12):70-75.

[5] 丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述 [J]. 电子科技大学学报, 2011, 40(1): 2-10.

[6] 肖智, 李文娟. 基于主成分分析和支持向量机的个人信用评估[J]. 技术经济, 2010, 29(3): 69-72.

[7] 张丽娜, 赵敏. 我国商业银行个人信用评分指标体系分析[J]. 市场周刊 (理论研究), 2007(8): 115-117.

[8] 蓝润荣, 程希俊. 基于改进 RBF 神经网络的银行个人信用评级 [J]. 中国科学院研究生院学报, 2013, 30(3): 298-303.

[9] 梁琪. 企业经营管理预警: 主成分分析在 logistic 回归方法中的应用[J]. 管理工程学报, 2005, 19(1): 100-103.[10]聂铭, 周冀衡. 基于 MIV-SVM 的烤烟评吸质量预测模型[J]. 中国烟草学报, 2015, 20(6): 56-62.

(编辑王小唯)

The research on methods of personal credit scoring combined model selection based on optimized index system

REN Xiao1, JIANG Minghui1, CHE Kai2, WANG Shang3

(1.School of Management, Harbin Institute of Technology, 150001 Harbin, China;2.School of Computer Science and Technology, Harbin Institute of Technology, 150001 Harbin, China;3.School of Materials Science and Engineering, Harbin Institute of Technology, 150001 Harbin, China)

Abstract:For precise estimation of borrowers’ personal credit and reasonable risk management of commercial bank, main models as well as problems are pointed out first. Next, to solve these problems, a modified algorithm is designed to compute a series of weights for indexes to satisfy different needs in different banks with various data and finally improve the accuracy of the model.

Keywords:risk management; personal credit; model for credit scoring; modified algorithm

中图分类号:F830.589

文献标志码:A

文章编号:0367-6234(2016)05-0067-05

通信作者:任潇, renxiao@hit.edu.cn.

作者简介:任潇(1983—)，女，博士后；姜明辉(1967—)，男，教授，博士生导师.

收稿日期:2015-10-22.

doi：10.11918/j.issn.0367-6234.2016.05.010