应用积分图的织物瑕疵检测快速算法

董 蓉, 李 勃, 徐 晨

(1. 南通大学 电子信息学院, 江苏 南通 226019; 2. 南京大学 电子科学与工程学院， 江苏 南京 210093)

应用积分图的织物瑕疵检测快速算法

董 蓉1, 李 勃2, 徐 晨1

(1. 南通大学 电子信息学院, 江苏 南通 226019; 2. 南京大学 电子科学与工程学院， 江苏 南京 210093)

为解决现有基于图像处理的织物瑕疵检测算法实时性较差、正确率偏低等问题，提出一种包含学习和检测2个阶段的瑕疵检测算法。通过对无瑕疵模板图像的梯度能量特征及其分布特性的学习，自适应获得检测阶段所需的参数。一方面利用积分图原理将任意大小的图像块内的求和运算化简为三次加法运算，快速提取织物图像的梯度能量特征，实现织物瑕疵的实时检测，另一方面利用核函数拟合特征参数分布，结合均值漂移法求解分布峰值获得自适应的瑕疵判定阈值参数，实现织物瑕疵的准确分割。通过实验将本文算法与现有基于局部二值模式特征、小波特征、规则带特征等算法进行对比，针对包含3种纹理6类瑕疵的织物图像数据集的测试结果显示，本文算法平均处理时间为56 ms，正确率为97%。

织物瑕疵检测； 积分图； 特征提取； 核函数； 均值漂移

传统纺织行业的瑕疵检测多以人工肉眼检测为主，由于人眼视觉易疲劳导致漏检，人工观察效率低，人力成本代价大，与大规模工业化生产极不协调。近年来，许多学者研究利用计算机视觉和图像处理算法自动进行织物瑕疵检测。对织物图像直接阈值化分割瑕疵的方法虽然操作简单[1]，但是仅对平纹、斜纹等灰度均匀、无纹理图案的织物有效。基于图像滤波的方法在频域提取织物纹理特征，如Gabor滤波[2]、小波变换[3]，由于瑕疵尺度方向未定，滤波时往往需要提取多个尺度多个方向的结果作为特征向量，即便采用PCA降维方法，单帧图像检测时间仍需数十秒[2]，若直接选择某个滤波分量通过阈值分割来提取瑕疵，可降低运行时间[3]，但瑕疵存在于哪一阶分量具有不确定性。基于图像分解的方法利用二维经验模态分解[4]、奇异值分解[5-6]等手段将织物本身纹理结构分量与瑕疵分量分离，但是彻底消除织物本身纹理结构分量会导致漏检较小瑕疵。基于信号统计的方法在空间域统计织物灰度分布特征，如局部二值模式(local binary pattern，LBP)特征[7]、灰度共生矩阵特征[8]、规则带(regular band，RB)特征[9]等，统计特征具有较好地鲁棒性，但统计特征提取时一般需要利用邻域多个像素数据，如不采用合适的加速策略将导致整体运算量骤增，其中RB算法因为仅利用均值、方差等便于计算的灰度分布特征，实时性相对较强。基于纹理建模的方法如利用高斯马尔科夫随机场建立特定织物纹理模型，通过度量待检测图像的模型统计量与标准统计量的相似性来识别瑕疵，但受模型精度限制，不易识别小疵点和分散疵点[10]。基于聚类的方法[11]将织物背景和瑕疵视为2个类别进行区分，但需先行采用适宜的算法抑制背景纹理，一般的滤波算法对平纹斜纹等简单纹理能够抑制，但对复杂图案纹理背景难以有效。

为实现自动瑕疵检测算法的工业化应用，实时性和正确率都需满足，而据统计，仅有少部分算法能够满足实时性，而其中检测正确率高于90%的算法更是寥寥[12]。有学者考虑采用硬件加速以保证算法实时性，如基于DSP平台的自动验布系统[13]，可实现100 ms/帧的在线检测，该算法直接对小波高频系数阈值化来检测瑕疵，仅对断经瑕疵有效。另有采用GPU硬件加速实现在线检测[14]的算法，以纱线交点识别和纱线轨迹跟踪为基础，以经线在上时的经纬交叉点为特征点，专门针对平纹、斜纹、缎纹等简单纹理织物。为保证检测地正确性，一方面所采用的特征应当能够有效区分瑕疵和非瑕疵像素，另一方面，应当设计合适的计算策略获得用于瑕疵判定的阈值参数并使其具有自适应性。

本文提出一种基于积分图的快速织物瑕疵检测算法。利用积分图将任意大小的图像块内的求和运算化简为三次加法运算，快速提取梯度能量统计特征，极大减小运行时间，并利用核函数拟合非对称特征分布获得自适应的瑕疵判定阈值，实现瑕疵区域的准确分割。

1 算法架构

图1示出本文的算法框图，主要分为学习和检测2个阶段。在学习阶段，对无瑕疵模板图像处理，统计其梯度能量的核密度分布函数，采用均值漂移方法获得分布峰值以及方差参数作为检测阶段的自适应阈值；在检测阶段，对待检测图像，首先通过积分图算法求取每个像素点所在窗口的梯度能量，结合学习阶段的阈值参数，判定当前像素点是否是疵点，最后统计整幅图像的疵点总数来判定当前图像是否为瑕疵织物。

2 基于积分图的快速瑕疵检测

积分图是为了快速计算图像上任意矩形区域内像素积分而提出的一种算法[15]。对图像G(x，y)，其对应的积分图I(x，y)定义为

(1)

即积分图I中任一点(x，y)的数值为图像G中左上角至当前点(x，y)所构成的矩形框内所有点的像素值之和。为了加速运算，积分图可以用式(2)所示的快捷算法获得。

I(x,y)=I(x-1,y)+I(x,y-1)-I(x-1,y-1)+G(x,y)

(2)

已有积分图I(x，y)，图像G(x，y)上任意矩形区域的像素积分可由I(x，y)快速计算，如图2所示。令I(x1，y1)=R(A)，I(x2，y2)=R(A)+R(B)，I(x3，y3)=R(A)+R(C)，I(x4，y4)=R(A)+R(B)+R(C)+R(D)，R(·)函数表示区域积分，因此，D区域的积分R(D)可用式(3)计算。

(3)

根据式(3)，不管矩形区域D面积有多大，都仅需3次运算即可求取其中像素值之和，极大地降低了计算量。

一般而言，无瑕疵的织物图像纹理呈周期均匀分布，对其任意点(x，y)，以该点为中心计算固定大小w*h窗口下的能量，w、h分别为窗口的长、宽，理想状态下，该能量特征应当不随(x，y)的变化而变化，而瑕疵的出现将打破其周期性、均匀性，也使得能量分布发生变化。据此，采用窗口能量值作为特征描述来检测瑕疵，但考虑到能量值易受光照影响，本文采用梯度能量，先求取原始图像F(x，y)的梯度图G(x，y)，再对G(x，y)提取能量特征E(x，y)用于瑕疵检测。

基于以上原理，利用积分图进行瑕疵检测，具体步骤如下。

1) 求取待检测图像F(x，y)的梯度图G(x，y)；

2) 根据式(2)求取G(x，y)的积分图I(x，y)；

3) 对任意点(x，y)求取其梯度能量E(x，y)，即以点(x，y)为中心的大小为w*h的窗口区域内的像素积分

(4)

4) 如果E(x，y)满足下式，则点(x，y)为疵点。

或

(5)

式中：μ、σ1、σ2为通过对无瑕疵模板图像训练而获得的阈值参数，α为控制系数。

5) 统计待检图像F(x，y)中总疵点数，若大于阈值Td则判定该图有瑕疵。

3 基于核函数的阈值参数学习

理想状态下，对无瑕疵图像，梯度能量E(x，y)应当不随(x，y)的变化而变化，而实际上织物在不同区域的纹理不可能完全一致，图像采集过程中也可能引入噪声，因此，梯度能量E(x，y)往往呈一定分布形态，如图3所示。为获得式(5)中的阈值参数μ、σ1、σ2，一种最直接的方法是利用高斯模型来拟合E(x，y)的分布，并将μ、σ1、σ2设置为该高斯分布的均值和方差。然而，E(x，y)的分布并不总是具有对称性，在密度峰值的两侧可能呈现不同的衰减特性，因此，如果用具有对称性的高斯模型拟合很容易产生偏差，高斯拟合结果明显偏离真实分布如图3所示。

为此，本文提出采用核函数来拟合梯度能量分布，获得它的核密度概率分布P(e)[16]为

(6)

式中：N为该类织物无瑕疵图像的像素数，{en|n=1、2、3、…、N}，为无瑕疵图像中每个点的梯度能量数据；b为核函数带宽；c0为归一化系数；k(e)为核轮廓函数，本文选择高斯核轮廓函数，即k(e)=exp(-e/2)，e≥0。为获得梯度能量分布的峰值所在位置，利用均值漂移法[16]求取核密度概率分布P(e)的极值，根据密度峰值将能量分布分为左右两部分，分别计算各部方差用于瑕疵检测阈值的计算，具体步骤如下。

1) 设定初始值μ0为当前无瑕疵模板图像的梯度能量均值。

2) 令μ1=m(μ0)+μ0，其中m(μ0)为μ0处的均值漂移量[16]。

(7)

式中g(e)=-k′(e)。

4) 根据式(8)计算阈值参数。

(8)

5) 根据式(9)计算阈值参数。

(9)

为提高算法鲁棒性，对训练集中的无瑕疵图像依据式(7)～(9)求取阈值参数μ、σ1、σ2，再取其平均值作为最终瑕疵检测过程中的阈值参数。

4 实验及分析

为验证所提算法，利用香港大学电子电气工程系工业自动化研究实验室提供的织物图像数据集[9]进行测试。该数据集共有166幅图像，灰度均为256像素×256像素，包含方格(box)、点状(dot)、星状(star)3种织物纹理，囊括断线(broken end)、破洞(hole)、打结(knot)、重网(netting multiple)、粗条(thick bar)、细条(thin bar)6类织物瑕疵，并提供了可用于参数学习的无瑕疵模板图像以及真值图像(Ground Truth)。实验平台配置为：Intel i5-2410M处理器，主频2.3 GHz，内存4 GB。程序用MatLab 7下开发，窗口宽度和高度均设置为25，控制系数α设置为4。检测到的疵点显示为白点，否则为黑点。

图4～6示出数据集中的3种不同纹理的待测瑕疵图像、待测图像的梯度能量图、本文算法检测结果及真值图。由第2列梯度能量图可见，瑕疵区域的梯度能量特征与正常纹理区域有显著差别，说明所构建的梯度能量特征能够较好地区分瑕疵区域与正常纹理区域。与第4列真值图相比，第3列所提算法检测结果图能够较好地定位瑕疵，但是比真值图空洞少，这是因为真值图是利用人工对每个像素点独立判定是否瑕疵点，而所提算法提取特征时统计的是局部w*h大小的窗口内的特征，具有膨胀填充的效果。

表1示出不同纹理、不同类型瑕疵情况下，利用本文算法检测到的疵点数均值。由表可见，有瑕疵图像和无瑕疵图像的疵点数差异可观，当用于判定织物是否存在瑕疵的疵点数阈值Td为50时，错检图像仅5幅，正确率达97%。

表1 3类织物图像的疵点数均值
Tab.1 Average defective points among three kinds of fabric images

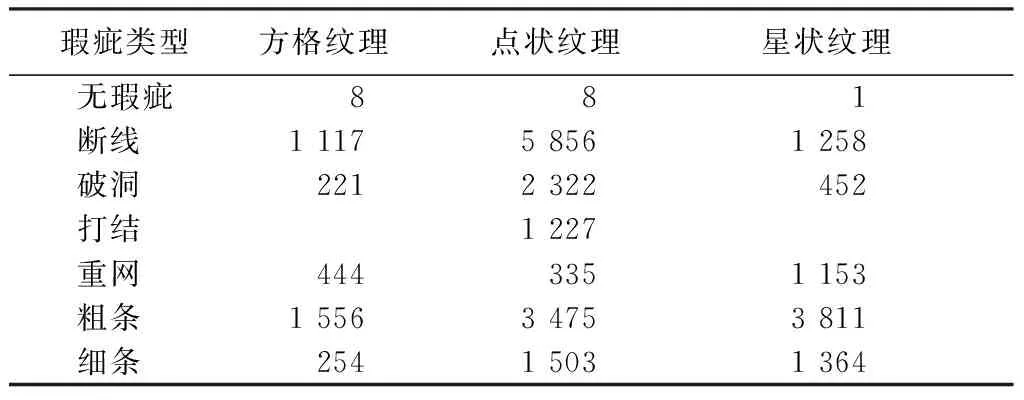
瑕疵类型方格纹理 点状纹理 星状纹理 无瑕疵881断线 111758561258破洞 2212322452打结 1227重网 4443351153粗条 155634753811细条 25415031364

图7～11示出本文算法与基于小波特征、基于LBP特征以及基于RB特征的检测结果对比。其中，小波特征向量由2层小波分解的水平、垂直、对角分量的方差组成，LBP特征向量采用8邻域均匀LBP(uniform LBP)直方图，提取特征的窗口大小均为25像素×25像素，判断是否疵点的阈值均调整为最优，RB算法采用原文中给出的结果。

另外，对各算法处理每幅图像平均需消耗的时间进行统计，在MatLab平台下，基于小波特征和基于LBP特征的方法分别耗时81 s和30 s，而本文算法仅需56 ms，RB算法是利用效率较高的C语言执行，但平均处理每幅图像仍需140 ms。由图7～11以及上述的消耗时间可见，基于小波特征、LBP特征的方法对像素是否疵点的区分能力不如本文算法以及RB算法。与RB算法相比，本文算法得益于积分图的加速功能，不仅能够准确定位瑕疵，且实时性更强。本文算法若转为C语言执行效率将更高。

5 结 论

织物图像瑕疵区域的梯度能量特征与正常纹理区域有显著差别，利用积分图算法可快速提取织物图像的梯度能量特征用于瑕疵判别，经统计平均运行时间仅需56 ms；采用普通高斯函数拟合梯度能量分布会导致误差，采用核函数拟合非对称的特征分布，结合均值漂移法提取分布峰值，可自适应求取阈值参数以准确分割瑕疵，正确率高达97%。本文方法既可满足实时性又具有较高正确率，并且能够适应不同纹理的织物，较为符合实际工业生产应用的需求。在以后的研究中，将进一步扩充现有织物图像数据库，以测试本文算法在各种不同类型织物下的适应能力。

FZXB

[1] 杜磊，李立轻，汪军，等. 几种基于图像自适应阈值分割的织物疵点检测方法比较[J]. 纺织学报, 2014, 35(6):56-61. DU lei, LI Liqing, WANG Jun, et al. Comparison of several fabric defect detection methods based on image self-adaptive threshold segmentation [J]. Journal of Textile Research, 2014, 35(6):56-61.

[2] BISSI L, BARUFFA G, PLACIDI P, et al. Automated defect detection in uniform and structured fabrics using Gabor filters and PCA [J]. Journal of Vision Communication and Image Representation, 2013, 24(7):838-845.

[3] 杨晓波. 基于自适应离散小波变换的混合特征畸变织物疵点识别 [J]. 纺织学报, 2013, 34(1):133-137. YANG Xiaobo. Research of mixture feature aberrance fabric defect recognition based on self-adaptive discrete wavelet transform [J]. Journal of Textile Research, 2013, 34(1):133-137.

[4] LI Z X, LIU J L, LIU J H, et al. Fabric defect segmentation by bidimensional empirical mode decomposition [J]. Textile Research Journal, 2014, 84(7):704-713.

[5] JAYANTA K C, ASIT K D. Detection of defects in fabrics using subimage-based singular value decomposition[J]. The Journal of The Textile Institute, 2013, 104(3):295-304.

[6] 王钢, 周建, 汪军， 等. 采用奇异值分解的机织物瑕疵检测算法[J]. 纺织学报, 2014, 35(7):61-66.

WANG Gang, ZHOU Jian, WANG Jun, et al. Woven fabric defect detection using singular value decomposition [J]. Journal of Textile Research, 2014, 35(7):61-66.

[7] 付蓉,石美红. 基于自适应LBP和SVM的织物疵点检测算法[J].计算机应用,2010, 30(6):1597-1601. FU Rong, SHI Meihong. Fabric defect detection based on adaptive LBP and SVM [J]. Journal of Computer Applications, 2010, 30(6):1597-1601.

[8] 邹超, 朱德森, 肖力. 基于模糊类别共生矩阵的纹理疵点检测方法[J]. 中国图象图形学报, 2007, 12(1):92-97. ZOU Chao, ZHU Desen, XIAO Li. Textural defect detection based on fuzzy label cooccurrence matrix [J]. Journal of Image and Graphics, 2007, 12(1):92-96.

[9] NGAN H Y T, PANG G K H. Regularity analysis for patterned texture inspection [J]. IEEE Transactions on Automatic Science and Engineering, 2009, 6(1):131-144.

[10] 杨晓波. 基于GMRF模型的统计特征畸变织物疵点识别[J]. 纺织学报, 2013, 34(4):137-142. YANG Xiaobo. Fabric defect detection of statistic aberration feature based on GMRF model [J]. Journal of Textile Research, 2013, 34(4):137-141.

[11] 张缓缓，李仁忠，景军锋，等. Frangi滤波器和模糊C均值算法相结合的织物瑕疵检测[J]. 纺织学报, 2015, 36(9):120-124. ZHANG Huanhuan, LI Renzhong, JING Junfeng, et al. Fabric defect detection based on Frangi filter and fuzzy C-means algorithm in combination[J]. Journal of Textile Research, 2015, 36(9):120-124.

[12] NGAN H Y T, PANG G K H, YUNG N H C. Automated fabric defect detection： a review[J]. Image and Vision Computing, 2011, 29(7):442-458.

[13] LI Y D, AI J X, SUN C Q. Online fabric defect inspection using smart visual sensors [J]. Sensors, 2013, 13(4):4659-4673.

[14] SCHNEIDER D, HOLTERMANN T, MERHOF D. A traverse inspection system for high precision visual on-loom fabric defect detection [J]. Machine Vision and Applications, 2014, 25(6): 1585-1599.

[15] BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF) [J]. Computer Vision and Image Understanding, 2008, 110(3):346-359.

[16] COMANICIU D, MEER P. Mean Shift: a robust approach toward feature space analysis [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5):603-619.

Fast fabric defect detection algorithm based on integral image

DONG Rong1, LI Bo2, XU Chen1

(1. School of Electronics and Information, Nantong University, Nantong, Jiangsu 226019, China; 2. School of Electronic Science and Engineering, Nanjing University, Nanjing, Jiangsu 210093, China)

The existing fabric defect detection methods based on image processing is poor in real-time performance and low in accuracy. In order to solve this problem, an algorithm consisting of two stages of learning and detection was proposed. By means of learning the gradient energy features and their distribution properties of non-defect model images, parameters in the detection stage were obtained automatically. On the one hand, by using integral image theory, summation operation in the image patch with arbitrary size was simplified to three addition operations, and gradient energy features in fabric images were extracted very quickly, so that fabric defects can be detected in real time. On the other hand, kernel functions were used to fit the distribution of feature parameters, mean shift method was used to solve the peak value in the distribution, and an adaptive threshold was obtained, so that fabric defect can be segmented precisely. In the experiments, the proposed algorithm was compared with the other three methods, respectively, based on local binary pattern features, wavelet features and regular band features. Tests on fabric image datasets including three kinds of textures and six kinds of defects show that the proposed method has an average running time of 56 ms and the accuracy rate is 97%.

fabric defect detection； integral image； feature extraction； kernel function； mean shift

10.13475/j.fzxb.20150704607

2015-07-21

2016-07-10

国家自然科学基金资助项目(61401239)；南通市应用研究计划项目(BK2014066)

董蓉(1984—)，女，讲师，博士。主要研究方向为计算机视觉、视频图像处理与模式识别。E-mail：drwistaria@163.com。

TN 911.73

A