服装工序相似性标准工时预测

王 玲， 杨以雄， 陈 炜

(1. 东华大学 服装·艺术设计学院， 上海 200051； 2. 东华大学 旭日工商管理学院， 上海 200051)

服装工序相似性标准工时预测

王 玲1， 杨以雄1， 陈 炜2

(1. 东华大学 服装·艺术设计学院， 上海 200051； 2. 东华大学 旭日工商管理学院， 上海 200051)

针对多品种、小批量的服装生产特征，在有效利用企业数据信息的基础上，为实现快速准确的工时预测、工时定额，提出基于服装工序相似性的预测工时新方法。将产品按照款式、部件、工序、工时进行划分编码，建立标准工时数据库，实现工时的快速查询。建立影响工序相似性的评价指标模型，借助主成分分析，获取各指标的权重，构建模糊隶属函数计算基准工序与样本工序的相似系数。借助MatLab软件进行曲线拟合，确立标准工时和工序相似系数的函数关系，以此预测工序工时。研究结果发现，13个工序相似性指标中，工艺内容指标权重最高为0.108，尺寸规格指标权重最低为0.011。通过案例企业实践应用，预测装拉链时间为201 s，与秒表测量时间208 s较接近，证实本文方法具有一定的准确性和可行性。

标准工时； 隶属函数； 服装工序； 主成分分析

服装制造业竞争激烈，面临着盈利空间受挤压、产品生产周期缩短，交货期不准确，生产计划编制复杂以及有效数据失真等问题。作为生产管理的数据基础和重要手段，服装标准工时的制定是服装企业进行科学化、标准化管理的重要依据，也是实现精益生产，提高企业竞争力和经济效益的有效途径[1]。

传统的工时制定方法多采用秒表法和预定时间标准法(PTS，predetermined time standards system)，通过对作业人员细致的观测，获取工时数据[2]。然而多品种、小批量、快交货的现代生产环境中，制造过程高度柔性化，生产工艺复杂的特点决定了传统的工时制定方法已不能满足企业和顾客对工时制定高效率和高精度的要求，因此，如何高效率、低成本地完成标准工时的制定成为重要的研究课题。Xia[3]与Sharafeev[4]提出工时计算可分为准确计算和模糊计算两部分，基于新的科学技术，利用程序软件实现计算，可较为准确地计算工时定额。Hur等[5]基于生产过程不同时间段产生的有效数据，建立了一种工时预测系统，并验证该方法在制造过程中的实用性。蒋麒麟等[6]基于案例推理和事物特征表，建立案例库，通过检索、匹配、修正，即可对工时进行估算。以上文献在工时数据库和数学模型的建立方面进行了积极探索，但是尚未细分到工序层面，均没有综合考虑加工工序对标准工时的影响。

服装生产订单多样化，但产品工艺和工序不尽相同，Chen等[7]提出零件加工的某些工序属于重复性工序，且同一工艺类型的工序间存在一定的相似性；阎树田等[8]根据相似学的基本原理，提出基于相似元的工序相似分析与评判方法；王共冬等[9]基于粗糙集理论，提出相似工序分类方法，通过工艺数据挖掘，获取工序的相似性特征对工时的影响。基于此，本文将相似性概念引入服装标准工时的预测，通过问卷获取工序影响指标权重，计算工序间相似系数，确定工时与相似系数的函数关系，为生产企业提供了快速预测产品工时的新方法，从而实现生产订单的快速反应和准时交货。

1 服装标准工时预测流程

根据企业实际情况和加工服装类型，本文设定的标准工时预测流程如图1所示。主要步骤如下。

1)建立服装标准资料库。根据服装款式特征，基于标准资料法，按照款式、部件、工序、工时进行细分，建立服装标准资料数据库，并对工序进行编码，对工时进行编码匹配，确定若干工序的时间以及未知工时的工序。

2)构建服装工序相似性评价模型。通过对未知工时的工序分析，确定工序所属工艺类型，探究服装工序的影响因素，通过专家问卷和主成分分析获取评价指标权重。在工艺类型中选择某道工序简单、工时已知且标准化的工序作为基准工序，选择若干工时已知的工序作为样本工序，分别计算样本工序、未知工时工序与基准工序的相似系数，依据MatLab软件绘制散点图，选择合适的曲线进行拟合，确定工时和工序相似系数之间的函数关系，最终获得未知工时工序的标准工时定额。

3)确定服装加工总工时。通过确定各工序的工时，从而获得服装加工总工时，提供生产计划编排、工序平衡的数据基础。

2 服装标准工时预测模型的建立

2.1 工序相似性影响因素分析

通常服装生产工艺比较复杂，一般影响服装加工工序的主要因素是面辅料种类、缝边长度、缝型、缝边形状、生产设备以及每道工序的质量标准[10]。本文从服装部件、工艺、设备、人员和环境等方面综合考虑，拟定的服装工序影响指标如表1所示。该指标体系包括部件特征、生产配置、作业标准、员工水平等5个一级指标和13个二级指标。对生产经验丰富的专业人员(以下称专家)进行问卷调查，获取各指标的权重信息。

2.2 基于主成分分析求解指标权重

计算权重主要有层次分析法、德尔菲法、主成份分析法等[11]，本文通过专家评分，运用主成份分析[12]求得权重。根据表1的工序指标评价体系制作问卷进行调查，在2015年3—6月，由20名专家采取五段量表对n(n=13)个影响指标进行重要性评分。当评分为5分时，即该项指标很重要，4分为较为重要，3分为一般，2分为不太重要，1分为很不重要。基于SPSS17.0软件对调查数据进行信度分析，得到克朗巴赫α系数值0.882，问卷信度良好，效度KMO值为0.747，基本适合进行主成分分析[13]，将13个二级指标提取出m(m=4)个主成分及各成分的初始因子载荷fij(i=1,2,…,n，j=1,2,…,m)和初始特征值λj(j=1,2,…,m)，如表2、3所示。

表1 服装工序的影响因素Tab.1 Influence factors of garment process

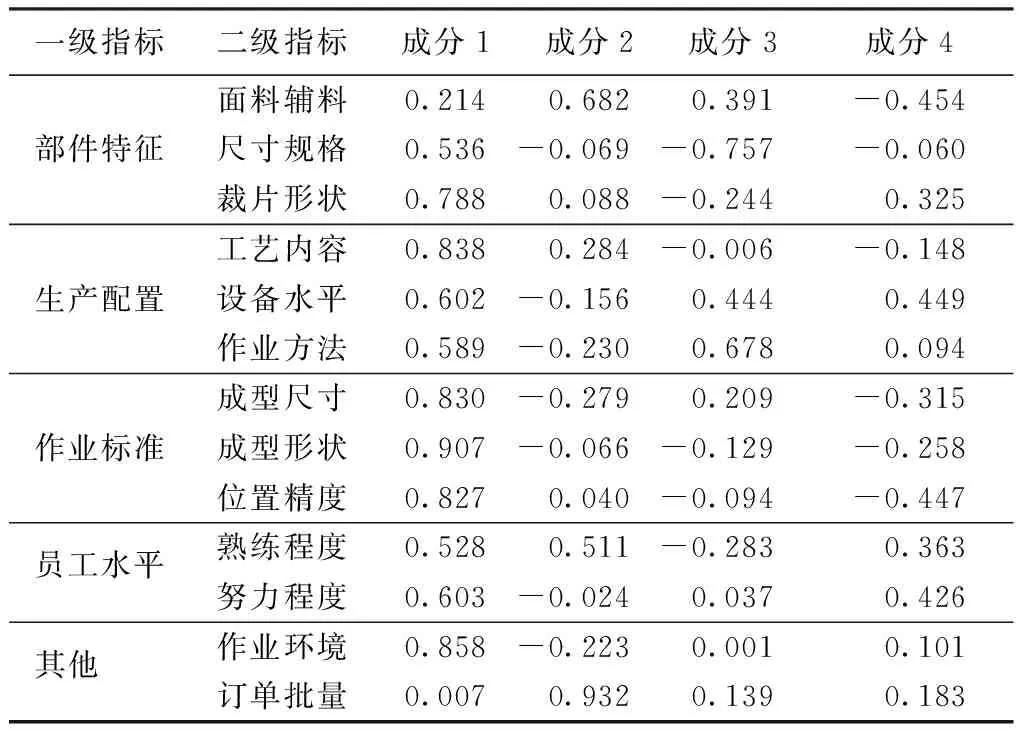
表2 成分初始因子载荷矩阵Tab.2 Component matrix

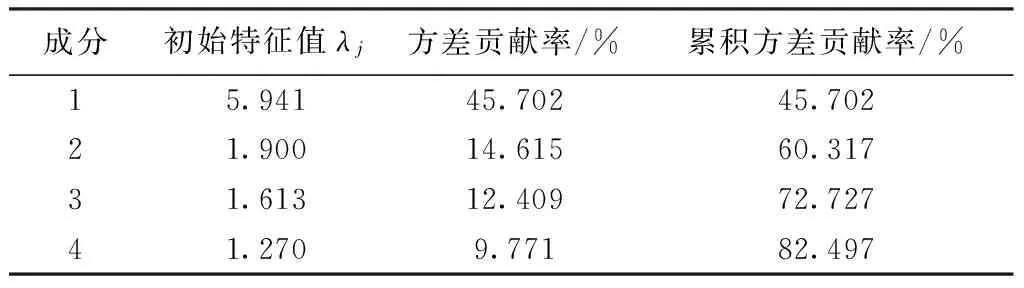
表3 主成分分析解释总方差Tab.3 Total variance of principal component analysis

将表2、3数据代入下式进行运算可得各成分系数tij。

将λj和tij代入下式求出指标在主成分中的综合重要度a1,a2,…,an。

通过下式对ai进行归一化处理，确定指标权重ωi(i=1,2,…,n)，如表4所示。

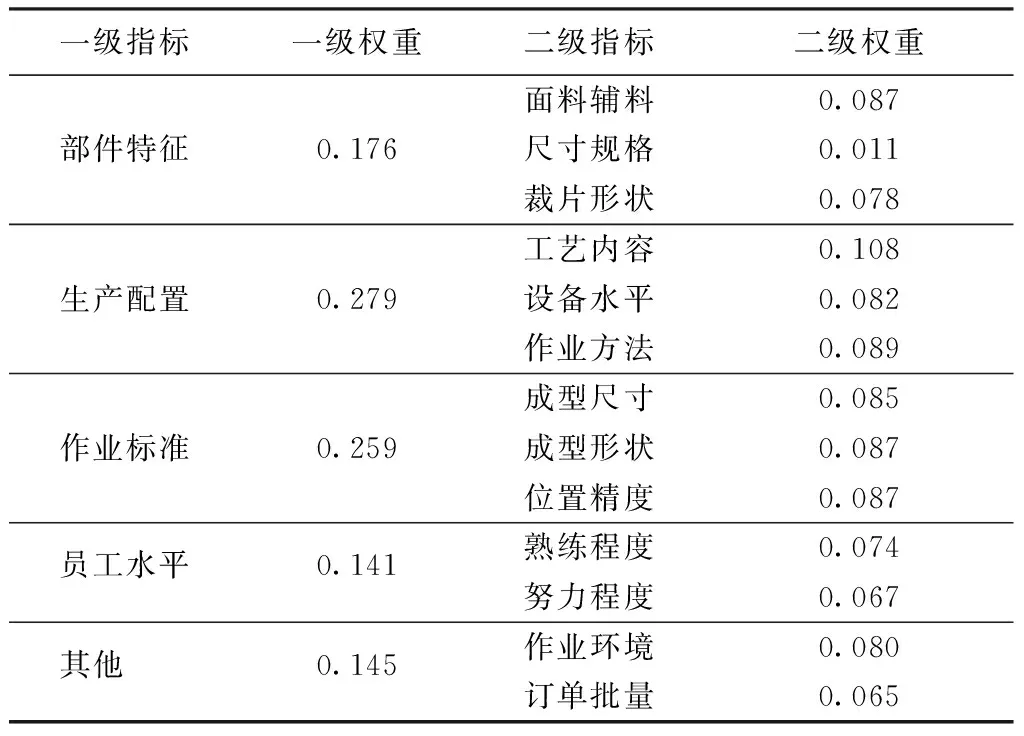
表4 各指标权重Tab.4 Index weight

2.3 服装工序相似系数计算

参与实践研究的Z企业以生产女装为主，该企业在多年生产实践中积累了一定的工时数据。为了合理安排生产，缩短交货期，需要预先确定款式的标准工时，以往单纯依靠样衣制作进行人工测定的工时制定方法，在准确性和应用性上存在一定的局限。为改善这种状态，以加工产品的特征和工时数据建立标准资料库，进而为基于工序相似性的标准工时制定提供基础，并探究该方法的可行性。以Z企业生产的亚麻连衣裙为例，流水线共20人，订单批量为820件。生产该款连衣裙共28道工序，通过工时匹配，其中装拉链的工序工时未知，各工序信息如表5所示。

装拉链(工时未知工序C)为平缝作业，由该款连衣裙平缝作业类型中选取k(k=11)个工序组成样本工序集B。其中，收省工序属于平缝，工艺简单，本文选择收省作为基准工序A，以此为例探究基于工序相似性的服装标准工时预测方法。

表5 亚麻连衣裙工序信息Tab.5 Process information of linen dress

基准工序A的n个评价指标构成矩阵X(x1,x2,…,xn)，xi(i=1,2,…,n)代表基准工序A的第i个评价指标标准值。同理，样本工序集B的n个评价指标构成矩阵Y。

式中：yij(i=1,2,…,n，j=1,2,…,k)为第j个样本工序的第i个评价指标标准值。

本文根据模糊统计法[14]，获取样本工序与基准工序的隶属度uij。

计算矩阵Y中元素的隶属度，得到隶属函数矩阵U。

经过模糊线性加权变换，即可得样本工序集B与基准工序A的相似系数矩阵：

(z1,z2,…,zk)

式中：ω1,ω2，…，ωn为各指标权重；uij为样本工序与基准工序的隶属度；z1,z2,…，zk为样本工序集B与基准工序A的相似系数。

在2015年4—6月期间，由15名专家采取五段量表对基准工序、样本工序及未知工时工序的13个指标对工时的影响程度进行评分，将获取的各工序指标标准值代入样本工序与基础工序的隶属度uij中，获得基准工序与样本工序的隶属函数U为

通过Z分别计算样本工序与基准工序的相似系数，同理可得到装拉链与基准工序的相似系数，具体数据如表6所示。由表可知，卷下摆工序相似系数最低为0.33，原因在于作业方法及作业标准等方面与收省存在较大差异和一定难度，且对员工技能水平要求较高。装约克工序在工艺内容、设备水平等生产配置及成形缝边尺寸与形状等作业标准方面与收省有一定相似，对员工技能要求相对较低，因此相似系数最高为0.91。

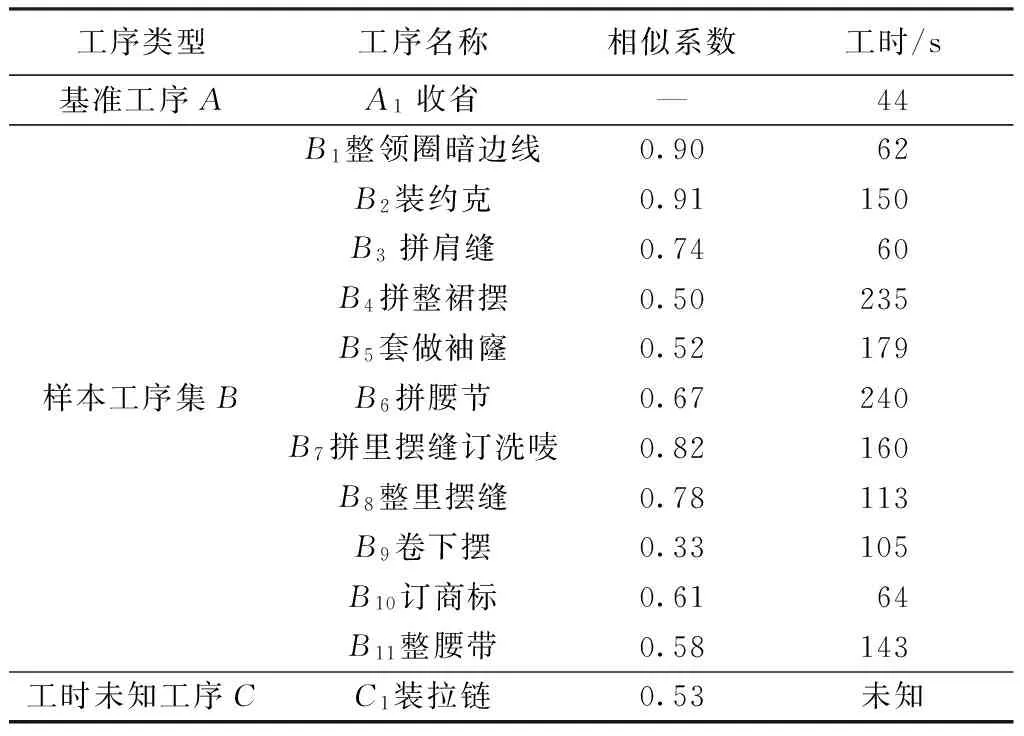
表6 工序相似系数Tab.6 Cofficient of process similarity

2.4 工序相似系数与工时曲线拟合

在实际应用中，通常需要探究2个变量之间的函数关系，然而一般只能获取或观测到部分数据点，针对离散的数据点，通过某种方法进行曲线拟合便可得到变量间的函数关系。MatLab软件具备强大的符号计算、数值计算和数据处理能力，可以快速实现参数拟合。

基于MatLab曲线拟合工具箱及表6数据，绘制样本工序工时与工序相似系数的散点图，依据散点图选择多项式、高斯函数及傅里叶级数等函数进行回归分析。运用五次多项式、二阶高斯函数、二阶傅里叶级数进行曲线拟合，拟合度分别为0.308 2、0.349 3、0.801 4，如图2～4所示。

由此可知，使用二阶傅里叶函数对平缝类工序工时和相似系数的拟合效果最佳，工时t和工序相似系数z满足以下函数关系

t=a0+a1cos(wz)+b1sin(wz)+a2cos(2wz)+b2(2wz)

式中：a0=149.3；a1=-50.11；b1=-40.89；a2=25.08；b2=-8.95；w=43.52。装拉链的相似系数为0.53，代入上式，得该工序工时为201 s。

3 预测工时与实际工时的对比分析

设n′为工序数量，则总工时为

式中ti(i=1,2,…,n′)为第i道工序的标准工时。结合表5，根据上式计算总工时为4 117 s。根据实地调研获得该订单1～6 d的实际日产量依次为0、78、134、142、150、152件。由于熟练率等原因，日产量从第3天开始趋于平稳，此时选择技能水平中等员工，利用秒表法对装拉链工序测时5次取算术平均值得到实际工时为208 s。根据第3天以后的产量数据可得平均日产量为144.5件/d。

式中：T′为实际标准总工时；T″为每天的工作时间；N为人数；Q为平均日产量；R为浮余率。

浮余率为浮余时间占工作时间的百分比[15]。实际观测获得Z企业浮余率为20.3%，每天工作时间为10 h，则实际标准总工时T′为4 142 s。根据秒表法和产量估算获取的工时对比结果如表7所示。

表7 工时对比Tab.7 Comparison of time quotas

从表1可以看出：本文提出模型预测的工时与实际工时比较接近，具有一定的准确性和应用价值，且节省大量观测时间；在确定各个作业种类工时与相似系数的函数关系的前提下，只需计算未知工序工时和基准工序工时的相似系数，代入函数即可，使工时预测方法更加便捷、准确。

4 结 论

考虑生产数据的浪费，服装标准工时的复杂性和重要性，本文通过实地调研案例企业并进行专家问卷，提出基于工序评价指标的工时预测模型，并与实际工时进行比较分析，得出以下结论。

1)从工序影响因素的角度建立5个一级指标，13个二级指标，一级指标中生产配置项权重最高，相应的生产配置下的工艺内容在二级指标中权重最高。

2)通过MatLab获取的工时与相似系数拟合度最佳的函数关系，得到的预测工时相对准确性较高。

在建立标准资料库的基础上，通过编码匹配，有效利用以往大量的工时数据，针对未知工时工序，以隶属函数表征工序与基准工序的相似性，曲线拟合确定工时与相似系数的函数关系，进而确定总工时的预测方法具有一定地便捷性和实用性。本文针对平缝作业种类，以收省基准工序为例，分析该预测方法的应用，后续将针对其他工艺种类进行研究，探索整件服装加工工时的预测问题，本文数据均来源于案例企业，在推广应用上有待进一步考证。

FZXB

[1] CHANG S K, CHA M S, RHO J J. A case study for determining standard time in a multi-pattern and short life-cycle production system[J]. Computers & Industrial Engineering, 2007, 53(2): 321-325.

[2] 叶宁, 阎玉秀. 多品种小批量服装生产的工时定额制定方法[J]. 纺织学报, 2012, 33(6): 101-106. YE Ning, YAN Yuxiu. Man-hour quota determination method for garment production of multi-variety in small batch[J]. Journal of Textile Research, 2012, 33(6): 101-106.

[3] XIA S, WANG Y. Development of man-hour quota management system of slewing bearings[J]. Journal of Anhui University of Technology, 2015, 32(1): 60-66.

[4] SHARAFEEV I S. Structure of technological-purpose automation models by the example of a computer-aided design system of labor standards[J]. Russian Aeronautics, 2008, 51(1): 105-108.

[5] HUR M, LEE S K, KIM B, et al. A study on the man-hour prediction system for shipbuilding[J]. Journal of Intelligent Manufacturing, 2015, 26(6): 1267-1279.

[6] 蒋麒麟, 薛小强, 李翔英. 基于实例推理的钣金件数控切割工时估算[J]. 制造技术与机床, 2014(4): 156-159. JIANG Qilin, XUE Xiaoqiang, LI Xiangying. Machine hour evaluation of sheet metal CNC cutting based on case-based reasoning[J]. Manufacturing Technology & Machine Tool, 2014(4): 156-159.

[7] CHEN Youling, REN Xiaojie. Time-quota computing method based on similarity coefficient of process[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 866-872.

[8] 阎树田, 赫川伟, 郭课. 基于物元理论的工序相似性识别方法[J]. 兰州理工大学学报, 2008, 34(6): 37-39. YAN Shutian, HE Chuanwei, GUO Ke. Similarity recognition operations on matter-element theory[J]. Journal of Lanzhou University of Technology, 2008, 34(6): 37-39.

[9] 王共冬, 赵新坤, 陈浩, 等. 粗糙集技术在回转体零件工时定额制定中应用[J]. 科学技术与工程, 2015, 15(15): 189-194.

WANG Gongdong, ZHAO Xinkun, CHEN Hao, et al. Rough set technology in calculation man-hour quota of rotary part[J]. Science Technology and Engineering, 2015, 15(15): 189-194.

[10] 许同洪. 面料的物理力学性能研究综述[J]. 国外丝绸, 2008(1): 30-31. XU Tonghong. Research on physical and mechanical properties of fabrics[J]. Silk Textile Technology Overseas, 2008(1): 30-31.

[11] MEO M, ZARZOSO V, MESTE O, et al. Catheter ablation outcome prediction in persistent atrial fibrillation using weighted principal component analysis[J]. Biomedical Signal Processing & Control, 2013, 8(6):958-968.

[12] 吴天福, 邓华强, 伍人涛. 基于主成分分析的力量结构指标权重计算[J]. 微计算机信息, 2009, 25(16):264-265. WU Tianfu, DENG Huaqiang, WU Rentao. Calculation of the fore structure′s weight based on PCA[J]. Micro-computer Information, 2009, 25(16): 264-265.

[13] 罗应婷, 杨钰娟. SPSS统计分析从基础到实践[M]. 北京: 电子工业出版社, 2010: 281-303． LUO Yingting, YANG Yujuan. SPSS Statistical Analysis from Basic to Practice[M]. Beijing: Electronics Industry Press, 2010: 281-303.

[14] 刘俊娟, 王炜, 程琳. 基于梯形隶属函数的区间数模糊评价方法[J]. 系统工程与电子技术, 2009, 31(2):390-392. LIU Junjuan, WANG Wei, CHENG Lin. Inter number fuzzy evaluation based on trapezoid subordinate func-tion[J]. Systems Engineering and Electronics, 2009, 31(2): 390-392.

[15] 杨以雄. 服装生产管理[M]. 上海:东华大学出版社, 2005: 250-256. YANG Yixiong. Garment Production and Manage-ment[M]. Shanghai: Donghua University Press, 2005: 250-256.

Prediction of garment standard time based on processes similarity

WANG Ling1， YANG Yixiong1， CHEN Wei2

(1. Fashion·Art Design Institute, Donghua University, Shanghai 200051, China； 2. The Glorious Sun School of Business and Management, Donghua University, Shanghai 200051, China)

With the multi-specification and small batch manufacturing, in order to achieve fast and accurate time-quota prediction, this study effectively uses enterprise data and proposes a new method based on similarity of processes. The products were encoded depending on styles, components and procedures, and standard time quota database was established to realize the work time quick inquiry. This paper established the model of the evaluation indicators for processes similarity, analyzed with principal component, obtained the weight of each index, and made fuzzy membership functions to calculate the similar coefficients of the benchmark process and sample process. The function relationship between the standard time quotas and the similar coefficients was determined to predict the unknown time by curve fitting with MatLab. The research results show that the highest index weight is the process(0.108), and the lowest index weight is the specification(0.011). In the case study the predicted time of ″zipper″ (201 s) is close to the actual time by stopwatch (208 s) which proves the high accuracy and feasibility of the method.

standard time quota; membership function; garment process; principal component analysis

10.13475/j.fzxb.20151003507

2015-10-20

2016-07-01

中央高校基本科研业务费专项资金资助项目(CUSF-DH-D-2014068)；上海市教委海派时尚设计及价值创造知识服务中心资助项目(13S1070241)；东华大学非线性科学研究所交叉项目(INS-1401)

王玲(1992—)，女，硕士生。研究方向为服装产业经济。杨以雄，通信作者，E-mail：yyx@dhu.edu.cn。

TS 941.63

A