模糊全概率公式及模糊贝叶斯公式的研究
2016-05-16吕振伟
吕振伟
(太原学院,山西 太原 030032)
1 引言
由传统的贝叶斯公式导出的贝叶斯网络(Bayesian Network)是 Pearl 提出的一种基于概率论和图论的不确定知识表示模型,它以其坚实的理论基础,知识结构的自然表达方式,灵活的推理能力,方便的决策机制而成为近年来人工智能、专家系统、模式识别等领域的研究热点。在医疗诊断系统、软件测试、网站的智能导航、电力系统的故障诊断等方面都有着广泛的应用[1]。普通贝叶斯公式参数的数目随着结点的扇入的增加成指数增长,对于许多规模很大的问题很不实用,而本文提出的模糊贝叶斯公式可以较好地解决这个问题。
2 模糊条件概率的定义
下面把定义2.1 模糊集合上的加法推广到二维模糊集合上:
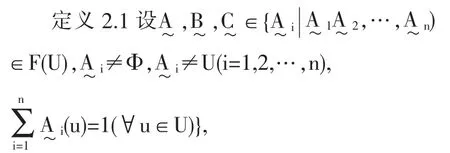
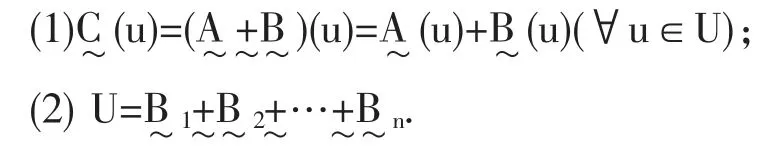
这个定义就是模糊集合上的加法,下面把这个加法推广到二维模糊集合上。

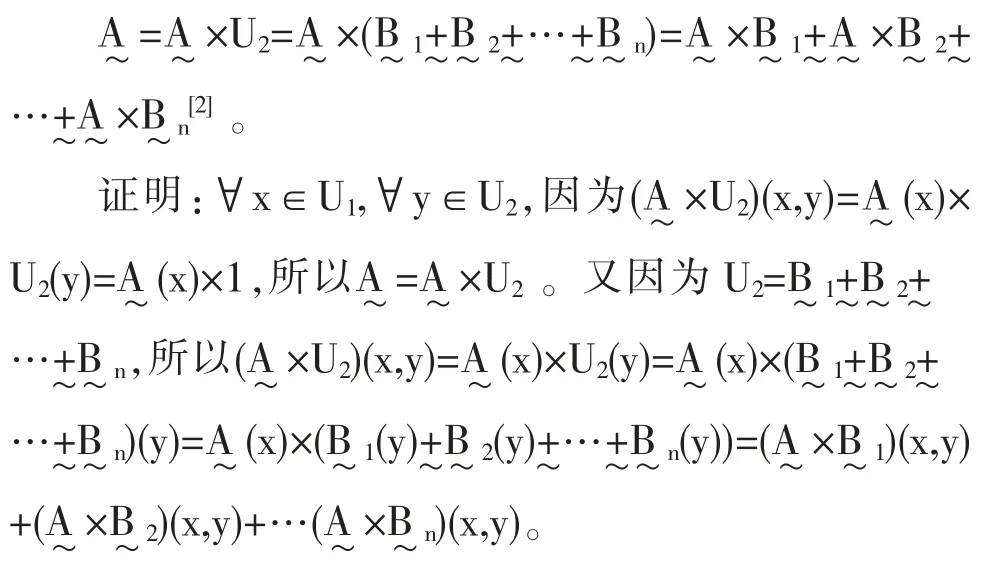
有了上述这些定义的基础,来定义在模糊数学里的条件概率公式的具体形式。知道在经典集合里概率中的条件概率公式为
定义2.3 设U1与U2为两个论域,则有二维论域为U1×U2上的二维模糊集,其隶属函数为
而在模糊概率中,集合已经由原来的经典的集合变为模糊数学中的模糊集合。也就是说那么知道,一般来说,与是属于两个论域的,则由上述定义2.3 推出如下定义:
上式称为模糊条件概率公式。
有了上述关于模糊条件概率公式的定义做为基础,通过一系列的推导可以得到如下定理:
定理2.1 模糊条件概率的性质如下:
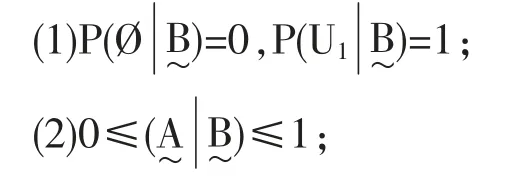
(3)对于属于一个U1的模糊划分的任意模糊集合和,



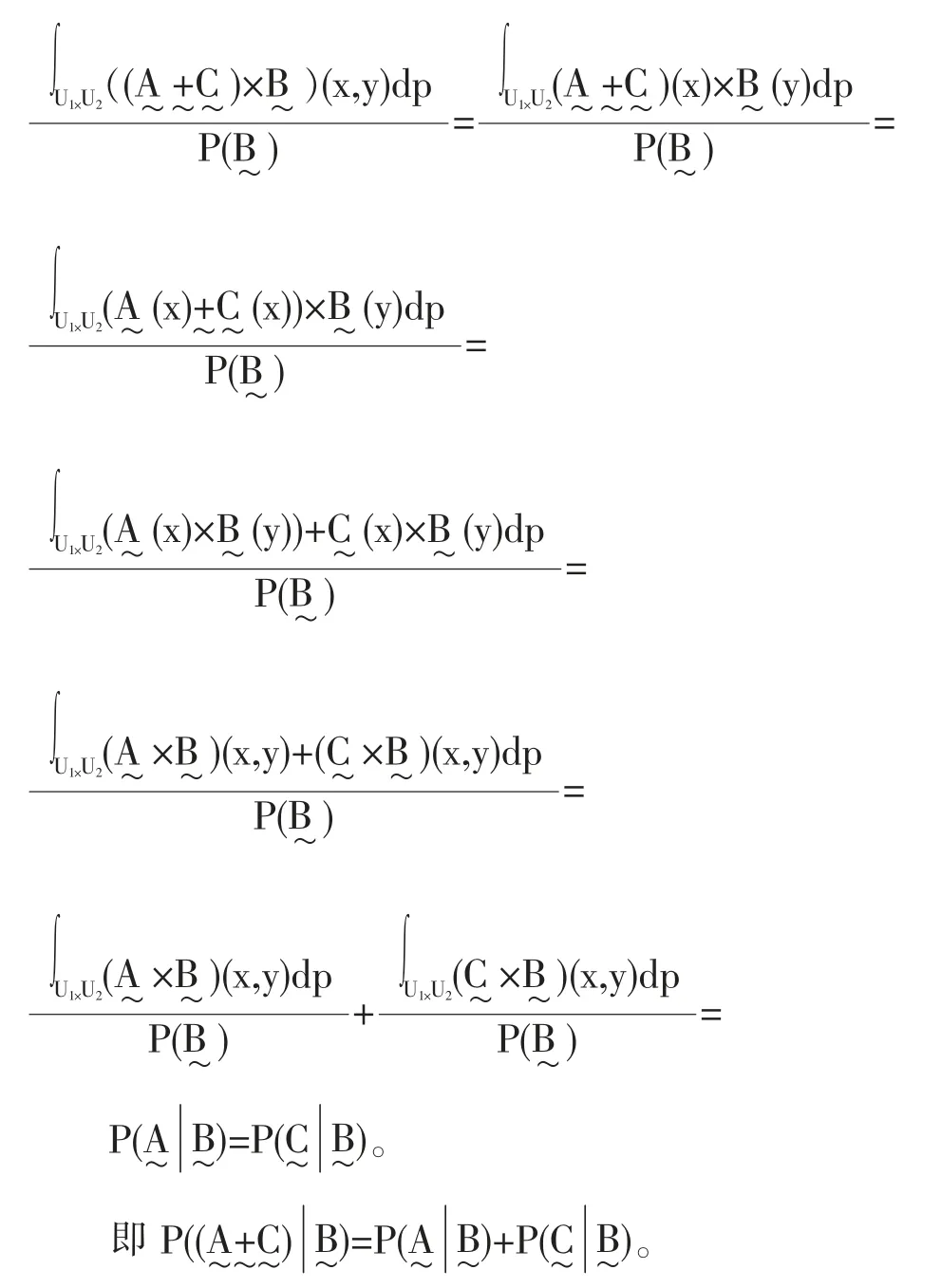


由上面所述,可以从下列的观点来考虑条件概率:
这种观点是可测空间(Ω,F)没有变,其概率变了,即P 换为,它对任意∈F 都有定义,并且概率空间由(Ω,F,P)变为
定理2.2[3]设为概率空间(Ω,F,P)上的正概率事件,又设则对条件概率空间而言,对任意∈F 有
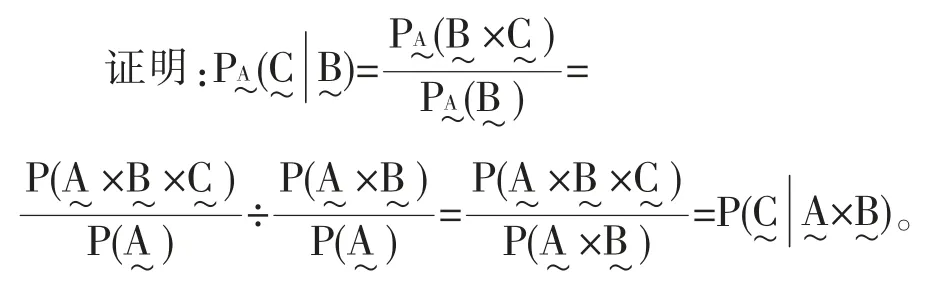
这个定理说明计算条件概率空间中任一事件的条件概率,可以转化为在原来的概率空间中求该事件的条件概率[6]。
3 模糊条件概率乘法公式
由条件概率定义,可得,
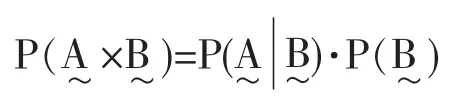
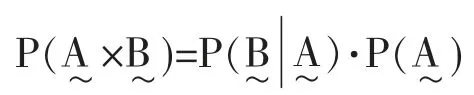
上面两个式子[7]均称为模糊事件概率的乘法公式。
上述乘法公式可以推广到任意有穷多个模糊事件时的情形。
对于上面得到的乘法公式,还可以得到如下的定理:
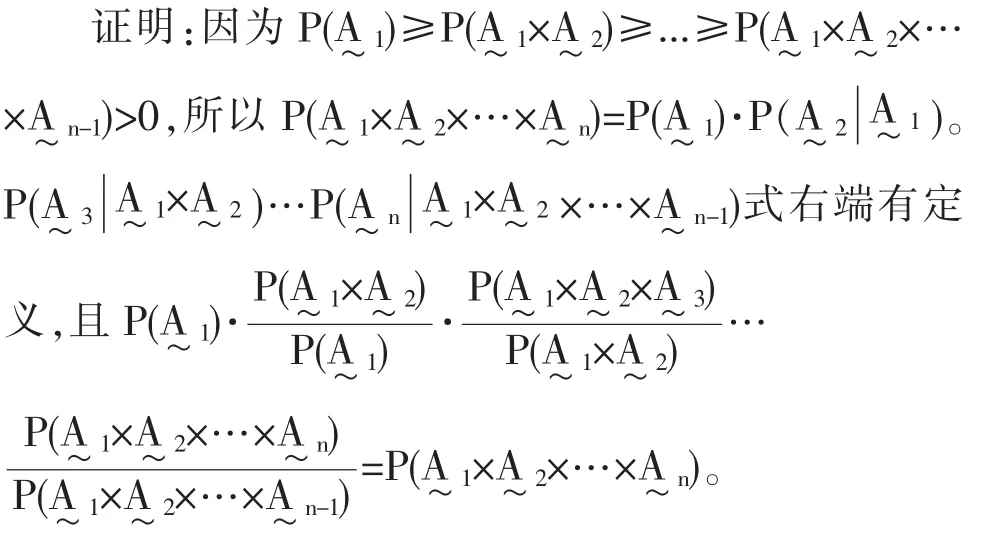
4 模糊全概率公式
下面继续讨论经典数学集合里的全概率公式在上述定义的基础上的具体形式。

我们还可以得出如下定理:

5 模糊贝叶斯公式
通过以上的推导,得到了乘法公式、全概率公式,那么进而可以得到在上述定义基础上的模糊贝叶斯概率公式:
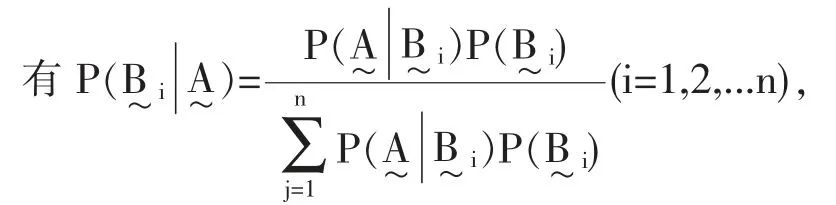
上式称为模糊贝叶斯公式。
证明:由模糊条件概率公式及全概率公式得
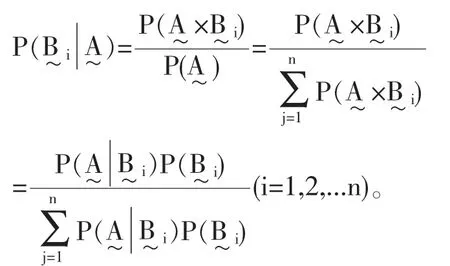
如果论域是连续的,那么模糊贝叶斯公式的具体形式是:
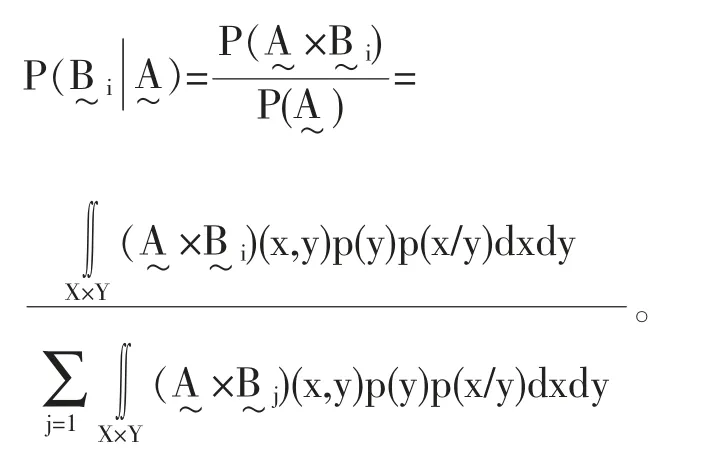
如果论域是离散的,那么模糊贝叶斯公式的具体形式是:
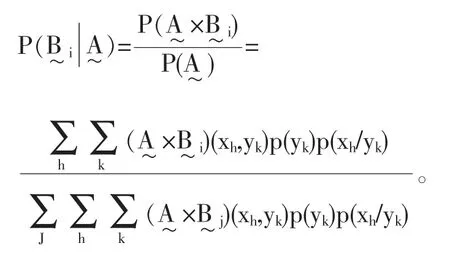
值得注意的是这个模糊贝叶斯公式是基于论域的模糊划分来得到的,所以尽管模糊集合之间会有交叉重叠的,但是我们得到的结果还是可以像经典集合上的贝叶斯公式有着相同的性质:在经典集合上的有穷剖分满足的条件,则通过贝叶斯公式所得到的各个结果之和满足如下公式:
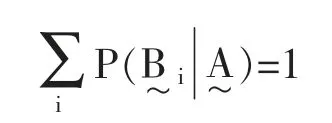
至此,我们证明了模糊贝叶斯公式。
6 举例验证
下面举一个离散情况下的例子。
假设身高 1.80,1.75,1.70,1.65 对模糊事件“高个子”的隶属度分别为 1、0.6、0.3、0,则模糊事件“高个子”的隶属函数表示为
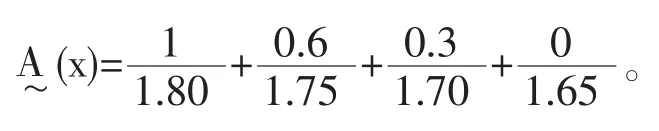
类似地,模糊事件成绩“优良”的隶属函数为
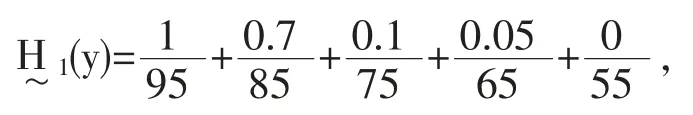
模糊事件成绩“中等”的隶属函数为
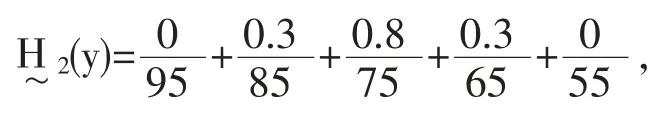
模糊事件成绩“较差”的隶属函数为

模糊事件“成绩优良的高个子”的隶属函数

从而,模糊事件“成绩中等的高个子”的隶属函数

模糊事件“成绩较差的高个子”的隶属函数
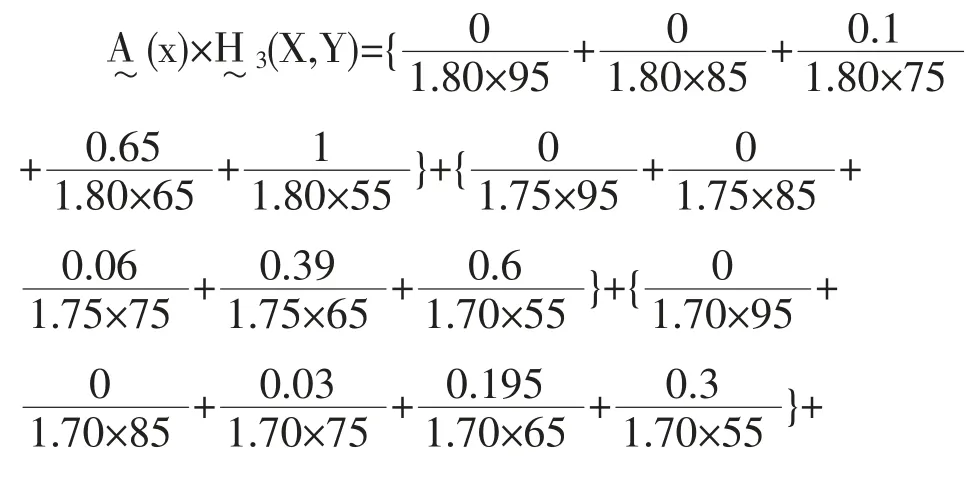
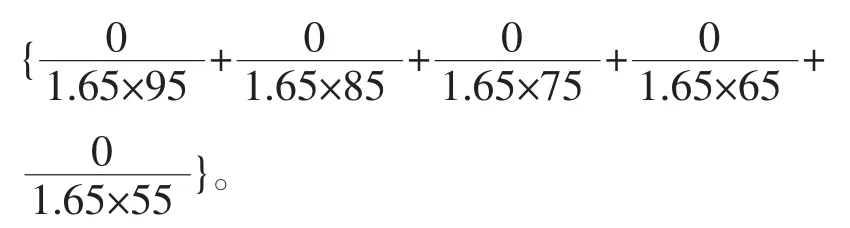

表6.1 假设该班男生考分的分布函数表
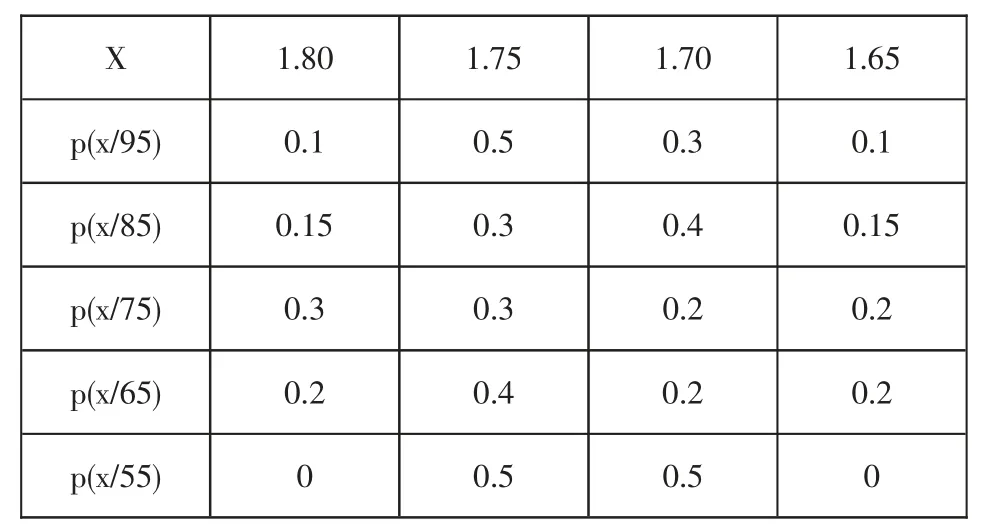
表6.2 假定身高对成绩的条件概率分布表
由以上已知条件,可得二维模糊事件的概率,
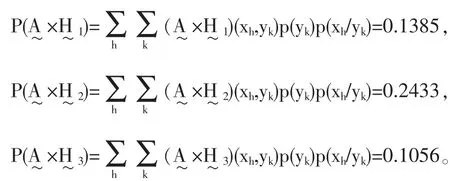
至此应用模糊事件贝叶斯公式就有

显然P(成绩优良|高个子)+P(成绩中等|高个子)+P(成绩较差|高个子)=1。
这也达到了预期的目的,即在模糊集合边界不明确的情况下还能保证贝叶斯公式最终求和值为1。
7 结论
在经典概率里,全概率公式得出的前提是要求有一组有穷剖分或者可列无穷剖分,然后通过这组剖分得出全概率公式和贝叶斯公式,而在模糊数学里,模糊集合之间的边界是模糊的,我们不能要求集合之间的交为空集,按照常规的方法所得到的贝叶斯公式来处理模糊数据时必定会有后验概率之和大于1 的情况。这种情况类似于经典概率里对样本空间的有穷剖分各个子集合之间的交不为空时,同样会导致经典贝叶斯后验概率之和大于1。
本文为了避免这种情况的发生,引入一簇模糊集合对一个论域进行划分,然后借助多维模糊空间得到了全概率公式和贝叶斯公式在模糊数学中的具体表达形式,最后通过数据验证确实在本文中得到的模糊贝叶斯公式能够有和经典数学里的贝叶斯公式相似的性质。本文所得到的模糊全概率公式和模糊贝叶斯公式是专门处理模糊事件的,而在实际中所得到的数据往往也是模糊的,所以更加切合实际。
