循环荷载作用下基床填料累积变形演化状态特征及试验验证
2016-05-15蒋良潍
罗 强, 刘 钢, 张 良, 蒋良潍, 熊 勇
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031; 2. 西华大学 建筑与土木学院,四川 成都 610039; 3. 西南交通大学 道路工程四川省重点实验室, 四川 成都 610031)
高速铁路路基是重要的线下基础结构形式,作为路基上部的基床结构,长期承受列车荷载重复作用,在100年的设计使用年限内,所承受荷载作用次数预估可超过“亿次”,使得对基床结构长期变形控制难度极大。目前,世界各国在高速铁路的修建中,多采用砾石类粗颗粒土作为基床填料,并大幅提高压实标准来应对这一工程问题[1]。这些措施主要以工程经验为主,理论分析相对不足。由于基床结构毫米级的变形,加之本构模型的不完善和计算参数较大变异性等因素的影响,精确计算和预测高周循环荷载作用下的累积变形存在很大困难[2]。因而,寻找一种力学机理清晰、方法简单明确的途径,解决基床结构长期累积变形的有效控制问题具有重要的现实意义。
有关循环荷载作用下基床结构的长期变形问题,张千里、胡一峰等[3-4]提出了基于应变控制法的解决思路,即以VUCETIC[5]所总结的临界体积应变为控制限值,以基床结构的动应变是否小于临界体积应变作为判别依据。这是目前解决基床结构累积变形问题的一种较为可行的思路。合理确定土工填料的变形状态控制参数是该设计思路的首要条件。众多研究表明,土工填料在不同应力水平的循环荷载作用下,随荷载作用次数的增加,其累积变形将呈现不同的状态特征。但是,有关循环荷载作用下土工填料累积变形演化状态的分类描述不尽相同。比如,HEATH[6]和蔡英等[7]分别对伦敦黏土和成都黏土进行了动三轴试验,荷载作用次数采用半对数坐标,根据累积应变曲线的发展规律将累积应变演化状态分为衰减和破坏2种类型;王龙等[8]针对公路基层所用的级配碎石材料,开展了常围压条件下动三轴试验,将累积变形曲线划分为稳定、衰减和破坏3种类型;WERKMEISTER等[9-12]通过对累积应变速率随荷载作用次数的变化规律分析,基于Shakedown理论进一步分析认为,随着应力的增加,累积应变将由塑性安定逐渐变化至塑性蠕变,直至最后达到破坏状态;MINASSIAN[13]以体积塑性应变为判别依据,将累积应变的演化划分为稳定、临界和不稳定3种状态。上述研究有关累积变形演化状态的区分与判别大多基于累积变形曲线形态变化或某种试验条件下的确定限值进行判别,缺乏普适性。此外,高速铁路对线下基础变形有严格的要求,有砟轨道与无砟轨道结构对路基变形的适应能力存在较大差异,在工务维修模式上也各具特点,基床填料在长期循环荷载作用下的累积变形演化状态应该如何分类、判别值得进一步探讨。
鉴于此,在总结已有研究成果基础上,结合高速铁路对基床结构的累积变形控制要求,对有砟和无砟轨道基床结构各自的累积变形演化状态控制要求及原则、累积变形演化状态的分类及判别准则进行了深入的探讨。此外,通过小型模型试验分析讨论用于高速铁路基床表层的级配碎石填料在循环荷载作用下的变形特性以及区分各状态的阈值。明确的状态控制原则、合理的状态划分及判别准则以及相应试验方法的提出可为构建基床结构长期累积变形状态控制设计计算方法提供参考。
1 累积变形演化状态分类及判别准则
1.1 累积变形演化状态分类
循环荷载作用下变形时程曲线见图1。每一次加卸载过程,变形都由可恢复的弹性变形和不可恢复的塑性变形2部分组成。其中弹性变形占绝大部分,塑性变形较小,但随着荷载作用次数的增加不断累积。

当级配、密度、含水率等物理特性相同,应力不同时,累积变形随着荷载作用次数的发展规律见图2。

由图2可知:在低应力时变形曲线形态很快趋于水平,如曲线①、②所示,表明累积变形将很快趋于稳定;中等应力时累积变形如何演化很难直观判定,曲线形态如③~⑥所示;较高应力时曲线形态如曲线⑦、⑧所示,累积变形快速发展直至发生破坏。
已有研究中循环荷载作用下累积变形演化状态分类情况见表1[6-14]。可见,应力较低时累积变形很快趋于稳定;应力较高时很快发生破坏。这是得到一致认可的观点。但对中等应力时累积变形最终演化状态的描述还存在较大差异,如HOFF、王龙认为将趋于稳定,WERKMEISTER认为将趋于破坏,MINASSIAN则认为最终状态难以界定。
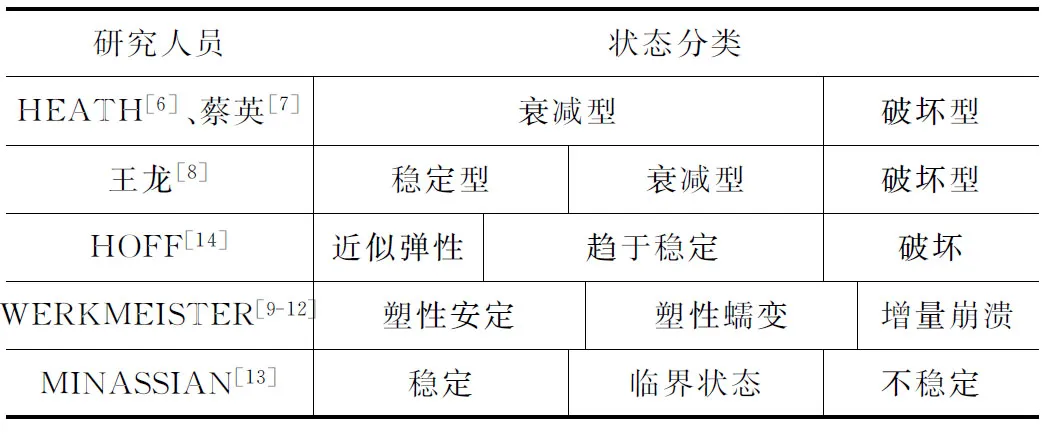
表1 循环荷载作用下累积变形演化状态分类
由表1可知,稳定与破坏是循环荷载作用下累积变形演化的2个最基本的状态特征,并且稳定与破坏间存在理论上的分界点。对于稳定与破坏,累积变形的演化也存在较大的时间尺度差异。综上认为,快速稳定、缓慢稳定、缓慢破坏、快速破坏4个状态可以更客观、全面地描述累积变形的状态演化特征,见图3。
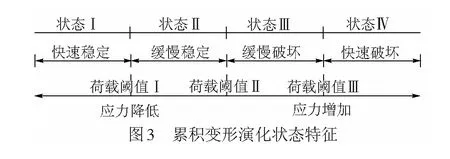
1.2 累积变形演化状态判别准则
分析发现,累积变形速率随荷载作用次数变化的曲线形态符合负幂律分布规律。因此,假定累积变形速率随着荷载作用次数的变化可以采用负幂函数描述为
f(N)=CN-P
( 1 )
式中:f(N)为累积变形速率;N为荷载作用次数;C为常数;P为幂指数。
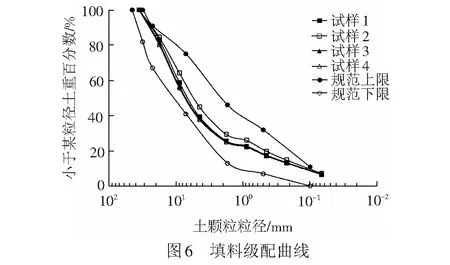
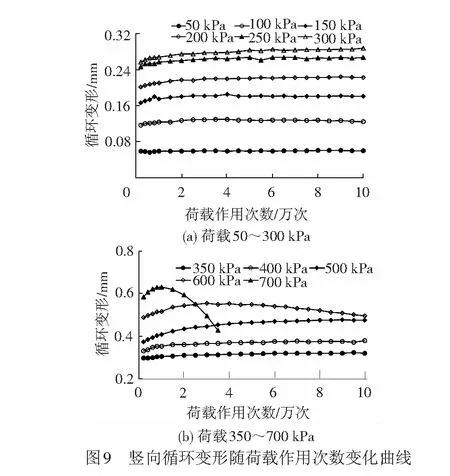
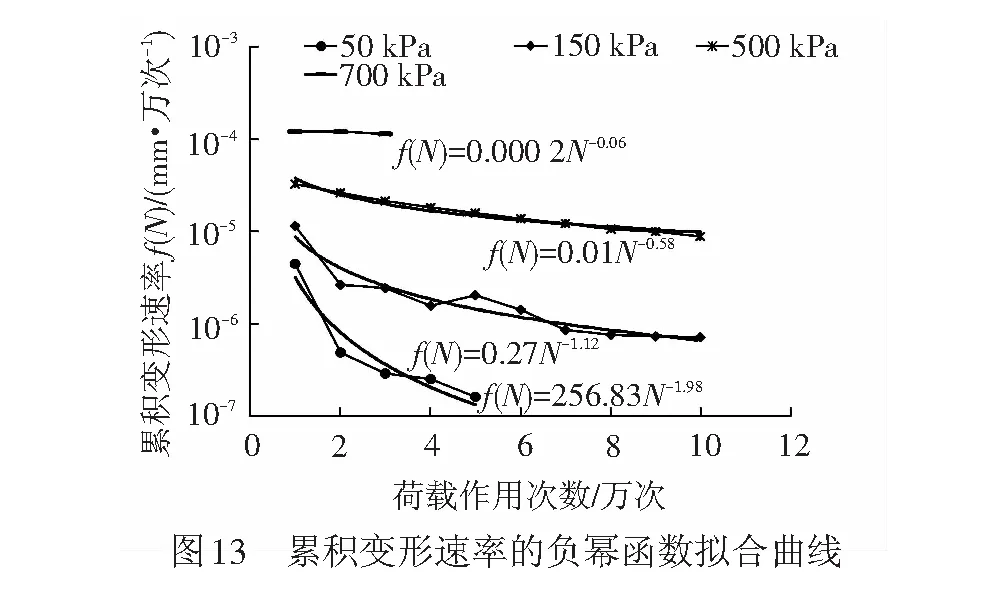
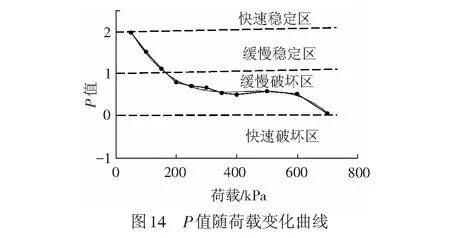
根据负幂函数的性质,累积变形速率衰减的快慢程度,可用幂指数P描述。P反映了累积变形收敛、发散或收敛发散快与慢等特征。P≥2时,变形速率呈现加速衰减趋势,累积变形快速趋于稳定;0 为验证关于循环荷载作用下路基填料累积变形演化状态特征以及相应判别准则的合理性,通过在室内构筑单元结构填土模型,采用直径为0.3 m的加载板进行循环加载试验,获得累积变形与荷载作用次数的关系曲线,分析其变形状态特征及荷载阈值。 有限元计算结果表明,直径0.3 m的均布荷载作用下,距中心点0.7 m、深度0.9 m处的应力衰减已达95%。因此,室内单元结构模型填土区域的几何尺寸为0.7 m×0.7 m×0.9 m(长×宽×高)。 模型结构见图5。 填土模型四周采用砖墙砌筑,砖墙4个角预留微缝,紧贴砖墙外采用砂袋整齐堆砌,形成非刚性的边界约束。 试验采用FCS多通道全数字电液伺服协调加载系统施加循环荷载,作动器额定最大输出荷载为100 kN,最大作用频率10 Hz。荷载施加从小到大依次进行,第1级荷载幅值为50 kPa,以50 kPa为级差逐级增加。加载至400 kPa时,按100 kPa荷载增量继续加载,直至填土模型破坏。循环荷载按正弦波变化,作用频率为5 Hz,每级荷载的加载次数为10万次。 在加载板东、西侧边缘处安装位移传感器,测试填土模型的竖向变形。另外在模型侧壁的东侧墙和南侧墙距填土表面分别为0.1、0.3、0.5 m处布设位移传感器,用于测试模型结构的水平向变形。位移传感器为非接触式电涡流位移传感器,由感应板和感应探头2部分组成。感应板与加载板或砖墙侧壁固定连接,感应探头固定于位移测试支架。位移测试支架与填土模型保持适宜的距离,以保证其不受加载的影响。 模型试验所用填料为级配碎石,参照文献[15]通过筛分试验确定填料的级配组成。填料最大粒径未超过40 mm,大于2 mm颗粒含量占总质量的73.5%,0.075~2 mm粒组的颗粒含量为19.6%,细粒(小于0.075 mm)含量为6.8%,不均匀系数Cu=68,曲率系数Cc=4.6,级配曲线见图6,满足文献[1]对基床表层填料的级配要求。 采用标准重型击实(Z3)[15],共计开展5组试验,共计25个试样,平行试验中最大干密度、最佳含水率的极差分别为0.054 g/cm3、0.95%。其中有2组击实曲线的最大干密度没有明显的峰值,对另外3组击实试验数据,采用三点二次插值函数法[16],计算得到最大干密度ρdmax为2.40 g/cm3,最佳含水率wopt为5.26%,填料击实曲线见图7。 模型内填土高度为0.9 m,分4层填筑,从下至上厚度分别为0.20、0.20、0.25、0.25 m。模型填筑时,砂袋周围用槽钢支挡,四面槽钢搭接处用螺栓固定,保证填筑过程中砖墙不发生水平偏移,砖墙内的填土空间体积不变化,以准确控制填土压实效果。填筑完成后松开螺栓。填土压实系数按K=1.0控制,填筑完成后,进行地基系数K30检测,其K30值为380 MPa/m。循环荷载施加过程中,加载板以外的模型填土表面采用塑料薄膜密封,以减小试验过程中水分的蒸发。 按试验设计对填土模型进行加载试验,共计加载11级,最大荷载为700 kPa时模型呈现出快速破坏的发展趋势。加载完成后模型表面状态见图8,表现为沿加载板板周以及模型“正十字”中心线出现明显裂缝。 2.3.1 循环变形和累积变形 竖向循环变形随荷载作用次数变化曲线见图9。当荷载较小时,整个加载过程中循环变形基本保持稳定;荷载大于500 kPa时,加载过程中循环变形出现较大波动;700 kPa循环荷载作用下,循环变形甚至出现了急剧增加至急剧减小的巨大波动过程。这种现象表明,土体结构已不能承受该荷载的持续作用,颗粒产生移动和重排列,土体结构发生变化。 模型填土循环变形(在加载次数内的平均值)随荷载变化曲线见图10。当荷载由50 kPa增加至700 kPa时,竖向循环变形由0.06 mm增大至0.57 mm;距顶面0.1、0.3、0.5 m处的侧向循环变形分别为0.012~0.368 mm、0.013~0.321 mm、0.009~0.229 mm,侧向变形由上至下依次衰减;随着荷载的增大,无论是竖向还是侧向循环变形均近似呈线性增加。 不同荷载时竖向累积变形随荷载作用次数变化曲线见图11,10万次(荷载700 kPa时为3.5万次)循环荷载作用下累积变形随荷载的变化曲线见图12。可知:随着荷载的增加,累积变形经历了由快速趋于稳定到快速破坏的发展过程;当荷载为50 kPa时、竖向累积变形仅为0.054 mm,基本没有侧向累积变形产生;荷载大于400 kPa后,竖向累积变形快速甚至呈近似线性增加,且有较大的侧向累积塑性变形产生;与循环变形不同,相同的荷载作用次数下累积变形随着荷载水平的增加呈现明显的非线性变化规律。 根据循环变形和累积变形的发展变化趋势,仅能从一般变形规律上作一些定性描述和分析,很难预测和判定累积变形的最终演化状态,尤其是在中等应力时定量的分析更难。 2.3.2 累积变形演化状态阈值确定 根据试验所得到的累积变形速率变化曲线,运用“幂次判别法”,可以得到每级荷载所对应的幂次值。荷载水平50、150、500、700 kPa时累积变形速率的拟合曲线见图13。4个荷载水平对应的P值分别为1.98、1.12、0.58和0.06,说明级配碎石在100%压实度条件下快速稳定状态的荷载阈值接近50 kPa,快速破坏状态的荷载阈值约为700 kPa。荷载为150 kPa时累积变形将最终趋于稳定,而荷载为500 kPa时将最终趋于破坏。 P值随荷载的变化曲线见图14,近似呈“倒S”形。P值的变化规律反映了累积变形状态演化的4个状态,即快速稳定、缓慢稳定、缓慢破坏和快速破坏。采用三次多项式进行拟合,计算P=0、1、2时所对应的荷载分别为σt3=712 kPa、σt2=168 kPa、σt1=50 kPa,即试验所用级配碎石填料在压实系数为1.0时,划分累积变形演化状态的荷载阈值。 根据文献[17]中地基系数K30与静允许承载力[σ]之间的经验关系式[σ]=2.4K30+15,换算得到级配碎石在该压实状态下(K30=380 MPa/m)的允许承载力[σ]=927 kPa,则荷载阈值σt1=0.054[σ]、σt2=0.18[σ]、σt3=0.77[σ]。 有砟轨道和无砟轨道是高速铁路采用的2种主要轨道结构形式,二者适应线下基础变形的能力、工务维修模式等均存在较大区别。有砟轨道散粒体道床属柔性结构,对路基的变形有一定的承受能力,而无砟轨道轨下的轨道板、支承层(底座)均由钢筋混凝土或混凝土组成,其整体刚度较大,线下结构不均匀变形很容易引起轨道结构与线下基础的“脱空”现象,对变形的适应能力相对较差。但是,有砟轨道结构较好适应变形能力的优点却导致了其保持线路稳定性和平顺性能力的降低,周期性的养护维修是线路良好运营的前提。无砟轨道结构以混凝土板作为轨下基础,显著增强了轨道结构的强度、刚度和稳定性,降低轨道结构的维修养护工作量。因而,日本将无砟轨道称之为“省力化轨道”[18]。但无砟轨道结构一旦损坏,其维修难度和成本相当巨大。鉴于有砟轨道与无砟轨道结构在适应变形能力及维修养护上的不同特点,对二者变形的控制应该有所区别。 考虑工程结构设计应遵循安全、适用、耐久、经济的基本原则,对于有砟轨道与无砟轨道基床结构,长期累积变形的控制不应采用相同的标准以实现安全性与经济性的统一。文献[1]规定对无砟轨道路基工后沉降不能超过15 mm,包含了地基、路堤和基床结构3部分。一般地基的工后沉降占据了主要部分,这就要求基床结构没有明显的累积变形发生。因此,无砟轨道基床结构需满足长期累积变形快速达到稳定。对于有砟轨道要求工后沉降的速率发展不能过快,否则导致维修周期缩短。因此,有砟轨道基床结构可允许有一定的累积变形产生,但累积变形必须逐渐趋近于稳定,即长期累积变形可按缓慢稳定进行控制。 综上分析,对于高速铁路,为使循环荷载作用下基床结构的累积变形能被有效控制,达到与轨道结构类型相适应的变形状态控制要求,在进行基床结构设计时应满足以下控制条件 σw≤σt1 ( 2 ) σy≤σt2 ( 3 ) 式中:σw为无砟轨道基床结构设计荷载;σy为有砟轨道基床结构设计荷载;σt1为荷载阈值Ⅰ;σt2为荷载阈值Ⅱ。 当采用级配碎石填筑基床结构、压实系数达到1.0时,无砟轨道基床结构在循环荷载作用下累积变形快速稳定对应的控制荷载阈值σt1=50 kPa。对于有砟轨道基床结构,累积变形长期稳定对应的控制荷载阈值σt2=168 kPa。当填料和压实状态变化时,可参照所述试验方法确定相应的荷载阈值,用于基床结构设计的填料参数选取。 基于对循环荷载作用下土工填料累积变形演化状态分类及判别准则的分析,通过填土模型试验对循环荷载作用下土工填料累积变形的状态演化特征进行了试验验证,探讨了高速铁路基床结构变形状态的控制原则及技术条件。结论如下: (1) 循环加载条件下,随着荷载水平的增加,土工填料累积变形的演化将依次呈现快速稳定、缓慢稳定、缓慢破坏、快速破坏的演化过程。建立了以累积变形速率为核心指标,以负幂函数f(N)=CN-P为数学表达式对累积变形演化状态予以判别的“幂次判别法”。 (2) 设计构筑了级配碎石填料在100%压实条件下的填土模型,对荷载由低到高循环加载过程中累积变形由快速稳定到快速破坏的全过程予以模拟。基于“幂次判别法”得到了试验条件对应的级配碎石填料4种变形状态的3个荷载阈值分别为50、168、712 kPa,其与基于K30=380 MPa/m的静允许承载力[σ]=927 kPa的比值分别为0.054、0.180、0.770。建立的基床填料变形状态荷载阈值试验方法为高速铁路基床结构变形状态设计的填料参数选取提供了依据。 (3) 基于高速铁路无砟轨道的耐久性受基础沉降的影响巨大、有砟轨道具有良好变形适应性的技术特点,给出了长期循环荷载作用下高速铁路无砟轨道基床结构累积变形应控制在快速稳定状态、有砟轨道基床结构累积变形需满足缓慢稳定状态的设计原则和技术条件,完善和发展了高速铁路基床结构的变形控制设计技术。 参考文献: [1] 国家铁路局. TB 10621—2014 高速铁路设计规范[S]. 北京: 中国铁道出版社, 2014. [2] 刘钢. 基于长期累积变形演化状态控制的高速铁路基床结构设计方法研究[D]. 成都: 西南交通大学, 2013. [3] 张千里, 韩自力, 吕宾林. 高速铁路路基基床结构分析及设计方法[J]. 中国铁道科学, 2005, 26(5): 53-57. ZHANG Qianli, HAN Zili, LV Binlin. Structural Analysis and Design Method for Subgrade Bed of High-speed Railway[J].China Railway Science, 2005, 26(5): 53-57. [4] 胡一峰, 李怒放. 高速铁路无砟轨道路基设计原理[M]. 北京: 中国铁道出版社, 2010. [5] VUCETIC M. Cyclic Threshold Shear Strains in Soils[J]. Journal of Geotechnical Engineering, ASCE, 1994, 120(12): 2 208-2 228. [6] HEATH D L. Design of Conventional Rail Track Foundation[J]. Institution of Civil Engineers Proceedings, 1972, 51(3): 49-57. [7] 蔡英, 曹新文. 重复加载下路基填土的临界动应力和永久变形初探[J].西南交通大学学报,1996,31(1):1-4. CAI Ying, CAO Xinwen. Study of the Critical Dynamic Stress and Permanent Stain of the Subgrade-soil Under the Repeated Load[J]. Journal of Southwest Jiaotong University, 1996,31(1):1-4. [8] 王龙, 解晓光, 巴恒静. 长期动载下级配碎石材料的塑性变形与临界应力[J]. 同济大学学报, 2010, 38(9): 1 293-1 297. WANG Long, XIE Xiaoguang, BA Hengjing. Critical Stress and Plastic Deformation of Graded Aggregate Material Under Long-term Dynamic Repeat Load [J]. Journal of Tongji University, 2010, 38(9): 1 293-1 297. [9] WERKMEISTER S, DAWSON A R, WELLNER F. Permanent Deformation Behavior of Unbound Granular Materials and the Shakedown Concept[J]. Journal of Transportation Research Board, 2001(1): 75-81. [10] WERKMEISTER S, DAWSON A R, WELLNER F. Pavement Design Model for Unbound Granular Materials[J]. Journal of Transportation Engineering, 2004, 130(5): 665-674. [11] WERKMEISTER S. Permanent Deformation Behavior of Unbound Granular Materials in Pavement Constructions[D]. Dresden:Dresden University of Technology, 2003. [12] WERKMEISTER S. Shakedown Analysis of Unbound Granular Materials Using Accelerated Pavement Test Results from New Zealand’s CAPTIF Facility[J]. Pavement Mechanics and Performances, 2006, 154: 220-228. [13] MINASSIAN G H. Behavior of Granular Materials Under Cyclic and Repeated Loading[D]. Alaska: University of Alaska Fairbanks, 2003. [14] HOFF I, BAKL∅KK L J, AURSTAD J. Influence of Laboratory Compaction Method on Unbound Granular Materials[C]//Proceeding of the 6th International Symposium on Pavement Unbound. Nottingham, England:A A Balkema Publishers, 2004. [15] 中华人民共和国铁道部. TB 10102—2010 铁路工程土工试验规程[S]. 北京: 中国铁道出版社,2010. [16] 冯忠居, 谢永利. 标准击实试验最佳含水量和最大干密度的理论计算[J]. 长安大学学报, 2002, 22(2): 10-13. FENG Zhongju, XIE Yongli. Numerical Method to Result Analysis of Indoor Standard Compaction Test[J]. Journal of Chang’an University, 2002, 22(2): 10-13. [17] 阚叔愚, 陈岳源, 周锡九, 等. 重载铁路工程[M]. 北京: 中国铁道出版社, 1994. [18] 日本铁道综合技术研究所. 铁道构筑物等设计标准及解说——土工构造物[Z].日本:丸善出版社,2005.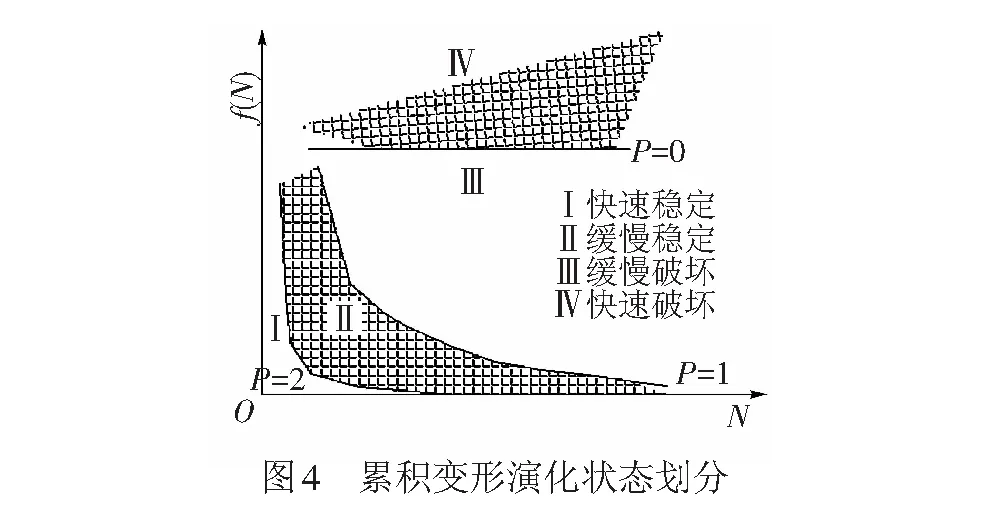
2 室内填土模型试验验证
2.1 试验设计
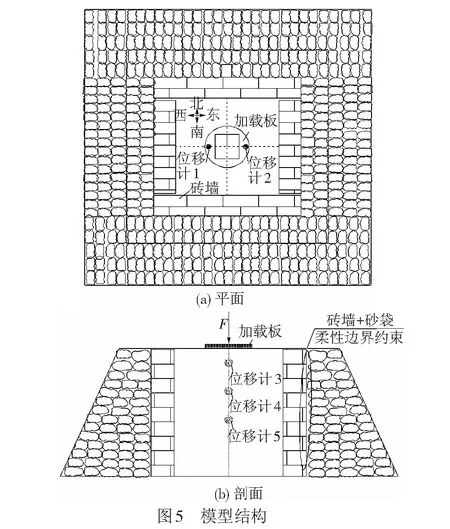
2.2 模型填料及填筑控制

2.3 试验结果分析




3 高速铁路基床结构变形状态控制原则及填料参数选取
4 结论
