考虑磨耗的钢轨疲劳裂纹萌生寿命预测仿真

周 宇， 张 杰， 王少锋， 姜俊楠， 于 淼

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.华东交通大学 轨道交通学院，江西 南昌 330013)

滚动接触疲劳(Rolling Contact Fagitue,RCF)裂纹和磨耗是影响钢轨寿命的主要伤损，两者相互影响，共同控制钢轨寿命[1]。大多数针对疲劳裂纹[2-4]和磨耗[5-6]的研究都是分别开展的，没有讨论彼此之间的关系。已有的讨论两者相互关系的文献是从经验和现场观测[7-8]或者实验室轮轮双盘滚动试验[9-10]来研究，缺少理论探索。在非铁路领域，MADGE等[11-12]采用Archard磨耗模型和临界平面法裂纹萌生预测模型分析了磨耗对Ti-6Al-4V合金疲劳裂纹萌生和扩展的影响。LEEN等[13]通过三维有限元模型研究了典型的航空发动机花键联轴器的疲劳和接触磨耗。ZHANG等[14]基于有限元方法对人工髋关节假肢之间的磨耗-疲劳裂纹相互影响进行了分析。而钢轨在轮轨反复作用下，其表面材料的磨耗和疲劳总是同时存在的，特别是硬质钢轨具有磨耗小、裂纹萌生早、扩展快等特点，已经严重影响使用寿命，有必要建立理论模型对钢轨的疲劳裂纹和磨耗的相互关系进行研究，探索两者的平衡关系和减缓措施。

本文根据Archard磨耗理论和临界平面理论分别建立钢轨磨耗模型和疲劳裂纹萌生预测模型，通过磨耗计算、型面变化和平滑、规定磨耗量的型面迭代、裂纹萌生预测和疲劳损伤累积，将车轮通过次数引起的疲劳裂纹萌生和磨耗发展的过程结合起来，建立考虑磨耗的钢轨疲劳裂纹萌生寿命预测方法，预测磨耗影响下的疲劳裂纹萌生特征。

1 考虑磨耗的钢轨疲劳裂纹萌生寿命预测方法

1.1 磨耗及型面预测方法

Archard磨耗模型认为材料的磨耗体积与硬度成反比，与法向力、滑动距离成正比[15]，即

Vm/D=K·N/H

( 1 )

式中:Vm为材料磨耗体积；D为滑动距离；N为轮轨法向力；H为材料的硬度；K为磨耗系数，其值由滑动距离和法向压力决定，本文根据文献[15-16]中的磨耗系数取平均值。

当考虑接触斑面积及接触斑的黏着-滑动区分布时，式( 1 )中的N由接触应力代替，则可以计算出接触斑内滑动区任意点的磨耗量，即磨耗深度。

接触点与接触斑关系见图1。当一个车轮滚过钢轨表面任意O点时，该点受到不同时刻轮轨接触斑A1、A2、A3…的分别碾压作用。假设该车轮在各个时刻产生的轮轨接触斑为稳态形式，即其轮轨正压力、蠕滑率、蠕滑力、接触面积、黏着-滑动区分布等参数不变。为计算一个车轮滚过O点的累积磨耗量，将可能的接触斑区域划分成m×n个单元格，如图2所示，O点的累积磨耗量就是所有接触斑通过该点所在单元格引起的磨耗量的累加。例如，假设该点位于接触斑中心，其累积磨耗量为经过该点所有纵向单元格磨耗量的累加，如图2中通过O点的纵向黑色条带。

因此，接触斑内任意点的磨耗为

( 2 )

式中:Δzys为接触斑第y个纵向条带的累积磨耗量；Δzs(x,y)为单元格(x,y)处的磨耗量；m为接触斑纵向单元格数量；n为接触斑横向单元格数量。

当一个转向架的前后2个车轮均作用在一股钢轨上时，如2个车轮作用在曲线外轨上，相应的轮轨接触斑位置、尺寸、黏着-滑动区分布及钢轨型面磨耗量见图3。其中，接触斑和磨耗深度图的坐标系原点在轨头中心线上，横向为钢轨横断面方向，纵向为列车运行方向。进一步，当1节车厢2个转向架4个轮对作用时，任意横断面钢轨磨耗量为4个车轮引起的累积磨耗量之和。

由图3可知，1个车轮作用下的钢轨磨耗量最大不到1.8×10-6mm。为提高计算效率，定义当1节车辆反复作用下1股钢轨上的4个车轮引起的累积磨耗量之和再乘以车轮通过次数得到总磨耗量。当钢轨最大总磨耗量(磨耗深度)小于0.04 mm时，型面不发生变化；当最大总磨耗量达到0.04 mm时，型面发生变化。因此，仿真中钢轨型面连续变化采用每次最大磨耗量为0.04 mm的型面分段迭代实现。这时将钢轨型面各点垂直方向减掉对应的磨耗量，形成磨耗后的钢轨型面。

特别地，当曲线半径小于600 m时，外轮-外轨特别是导向轮与外轨常发生2点接触(转向架自由内接通过曲线时)。这时，轨肩-车轮踏面接触点按上述方法计算磨耗量，而轮缘-轨侧的接触点由于为全滑动状态，主要引起外轨侧磨和型面改变，所以根据轮缘-轨侧接触斑面积、接触斑法向力(为轮轨横向力在接触斑内的分布)，按库伦摩擦理论计算出接触斑切向力分布，并进一步计算轮缘-轨侧接触点处引起的磨耗量，作为轨侧的磨耗量和磨耗控制点。

由于磨耗模型认为磨耗只发生在分布于接触斑两侧和后部的滑动区，钢轨型面在2个位置会引起较大磨耗，使得磨耗量直接叠加到前一个钢轨型面上造成型面不规则，因此，采用三次插值样条曲线法将磨耗后的型面进行平滑处理[17]。

以轮轨1点接触为例，型面平滑控制参数见图4。

图4中的控制参数具体为：

(1) 控制点。起点Ps为轨顶中心；终点Pe为轨顶面垂直向下16 mm处；磨耗计算得到的2个磨耗量峰值点P1和P2。

(2) 下降量d1和d2分别为P1和P2的磨耗深度，即标准75 kg/m钢轨型面对应位置上的垂直磨耗。

(3) 下降量所在位置L1和L2分别为P1和P2的横坐标。

(4) 样条曲线控制点密度。在图4所示坐标系下，横坐标0～34 mm范围内控制点间隔1 mm；横坐标34～36 mm范围内控制点间隔0.1 mm。

由于钢轨磨耗型面沿x轴方向的变化是无突变渐变过程，定义磨耗型面上各个控制点的下降方式为

( 3 )

相邻2个控制点(点i和点i+1)间的曲线方程为

y=F(x)=yi+Ci,1(xi+1-xi)+

Ci,2(xi+1-xi)2+Ci,3(xi+1-xi)3

( 4 )

式中:x为控制点的横坐标;Ci,1、Ci,2、Ci,3均为方程的系数。

令式( 4 )的二阶导数F″(xi)=Si。由于F(x)的一阶导数连续，即F′(xi-0)=F′(xi+0)。当相邻2个点之间的距离相等即hi=xi-xi-1=hi+1=xi+1-xi=h时，可得

Si-1+4Si+Si+1=6(yi+1+yi-1-2yi)/h2

( 5 )

因此，式( 4 )中的系数为

( 6 )

此外，图4中起点和终点处的一阶导数应该连续以保证磨耗部分与钢轨型面剩余部分曲线相切。当x=xi和x=x0时，从式( 5 )可得出其边界条件为

( 7 )

式中:μi=hi/(hi+hi+1)=(xi-xi-1)/(xi+1-xi-1),λi=hi+1/(hi+hi+1)=(xi+1-xi)/(xi+1-xi-1)=1-μi,当2个相邻点横坐标距离相等时，μi=λi=1/2,i=1,2,…,n-1。

至此，磨耗型面的平滑可由式(4)～式(7)得到。2点接触时，增加轨侧工作边的侧磨点作为第3个磨耗控制点。

1.2 裂纹萌生寿命预测方法

对于每一个磨耗型面，其对应的疲劳裂纹预测方法从临界平面法和能量密度法得到，其中疲劳参量为

( 8 )

式中：〈 〉为MacCauley括号，〈σmax〉=0.5(|σmax|+σmax)；σmax为裂纹面上的最大正应力；Δε为裂纹面上正应变幅值；Δτ和Δγ分别为裂纹面上剪应力幅值和剪应变幅值；J为材料参数。

疲劳裂纹萌生寿命预测时根据式( 8 )中正应力部分和剪切应力部分的关系，选取不同的裂纹萌生寿命预测公式,即

FPijmax=

( 9 )

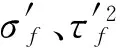
1.3 材料疲劳破坏累积方法

假设第i个型面被第i+1个型面替换前，共有ni次车轮通过，则第i个型面上第j点的无量纲的疲劳损伤为

Dij=ni/Nfij

(10)

假如型面上的第j点没有在磨耗过程中被磨掉，根据Miner疲劳法则，当∑Dj=D1j+D2j+…+Dij=DCR=1时，认为在第i个型面的第j点上裂纹萌生，裂纹萌生寿命为

(11)

式中：m为裂纹萌生时型面因磨耗而被替换的总次数。

1.4 考虑磨耗的钢轨疲劳裂纹萌生寿命预测流程

综上所述，考虑磨耗的钢轨疲劳裂纹萌生寿命预测步骤如下：

Step1以钢轨初始型面(如标准型面)为钢轨上道后的原始状态(i=1)，采用多体动力学软件建立车辆-轨道动力学模型，计算相应的轮轨力、接触斑位置和面积；采用Kalker轮轨蠕滑模型，计算轮轨法向力、蠕滑力及其在轮轨接触斑内的分布；当外轮轮缘-外轨轨侧出现第2点接触时，用库伦摩擦理论计算接触斑面积内法向力与切向力分布；当型面因磨耗而发生替换后(i=i+1)，同样根据上述方法计算对应型面的轮轨接触斑和轮轨力。

Step2采用式( 1 )、式( 2 )计算型面各点的磨耗量，当型面最大磨耗量没有超过设定的磨耗量(本文是0.04 mm)，型面不替换，同时累加车轮通过次数；当型面最大磨耗量超过设定的磨耗量，将型面各点磨耗量叠加到初始型面(或第i个型面)对应位置，采用式( 3 )～式( 7 )平滑型面，替换初始型面(或第i个型面)，得到第i+1个型面(计数为i=i+1)，同时得到该磨耗阶段的累积车轮通过次数，从而实现型面磨耗和分段迭代。

Step3结合钢轨初始型面(或第i个型面)，采用有限元方法建立钢轨全局模型和局部模型，全局模型用于计算局部模型的约束条件；局部模型用于施加接触斑内应力分布和约束条件，计算出轨头的应力应变分布。

Step5采用式(10)、式(11)计算疲劳阶段损伤Dij和疲劳累积损伤∑Dj。

Step6若疲劳累积损伤∑Dj小于DCR，则各点均没有萌生裂纹，继续按Step1～Step5条计算轨头各点的疲劳累积损伤；若疲劳累积损伤∑Dj等于或大于DCR，则认为在该点萌生裂纹，对应的各个磨耗阶段的累积车轮通过次数之和就是裂纹萌生寿命。

考虑磨耗的疲劳裂纹萌生预测流程见图5。

2 仿真结果

仿真计算时选用我国重载铁路小半径曲线常用的75 kg/m、U75V热处理钢轨。钢轨的基本力学参数取自文献[2]。钢轨为曲线外轨，曲线半径800 m，均衡超高，列车运行速度60 km/h。钢轨表面摩擦系数取0.3。

2.1 型面磨耗预测结果检验

对现场曲线外轨型面进行了测量，测量时间分别为新轨上道和通过总重约10×107kN时，期间车轮通过次数约6×105次。将2次测量的型面数据插值平滑处理，得到通过总重为1×107kN(车轮通过次数约6×104次)时的钢轨磨耗型面，作为实测磨耗型面。同时，采用1.1节的磨耗及型面预测方法预测车轮通过约6×104次时的钢轨型面。预测磨耗型面与实测型面的对比及其一阶导数变化趋势见图6。

由图6(a)可知，预测的磨耗型面与实测型面相差很小。对这2个型面进行离散分析，相同横坐标处的纵坐标偏差平均值为0.009 mm，各点偏差的方差为7.42×10-5。进一步分析轨距边一侧型面的一阶导数，对比两者的曲线变化趋势，如图6(b)所示，两者一阶导数偏差的平均值为0.002，一阶导数偏差的方差为4.44×10-6,说明预测的磨耗型面与实测磨耗型面基本接近。

2.2 考虑磨耗的裂纹萌生位置及寿命

在考虑磨耗的情况下，预测得到钢轨型面经过7次迭代，即7次型面磨耗，裂纹出现萌生。考虑磨耗的裂纹萌生寿命计算结果见表1。

表1 考虑磨耗的裂纹萌生寿命计算结果

由表1可知，随着磨耗的增加以及型面的迭代，接触斑内应力呈增加趋势，且初期缓慢增加，后期快速增加，最终导致疲劳累积达到临界值(DCR=1)。

考虑磨耗情况下钢轨轨头疲劳累积损伤量分布见图7。可知，疲劳损伤主要分布在轨顶面以下12 mm、距离轨顶中心10～25 mm处。其中最大疲劳累积损伤量所处位置就是裂纹萌生的位置。考虑磨耗和不考虑磨耗2种方法预测出的外轨裂纹萌生寿命及位置见表2。

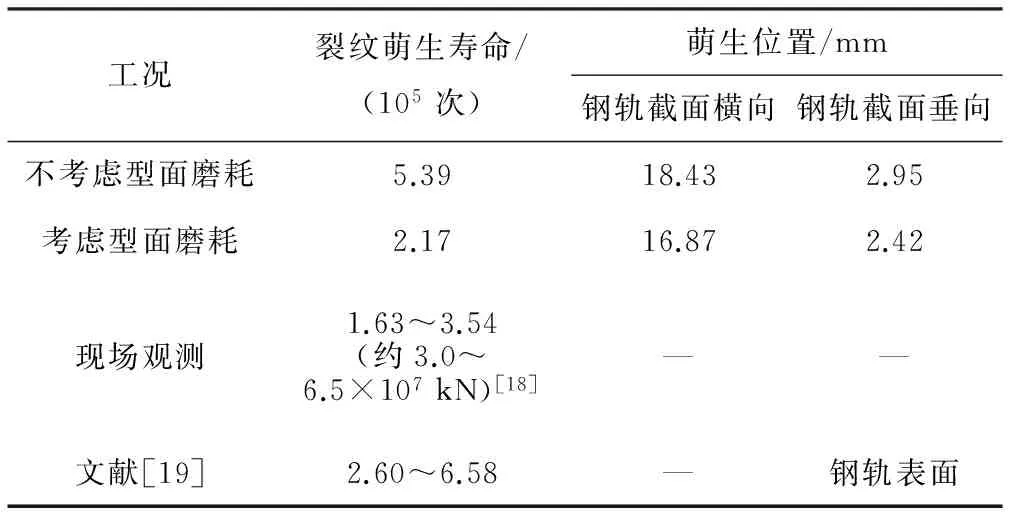
表2 考虑磨耗和不考虑磨耗情况下外轨疲劳裂纹萌生寿命及位置

工况裂纹萌生寿命/(105次)萌生位置/mm钢轨截面横向钢轨截面垂向不考虑型面磨耗5.3918.432.95考虑型面磨耗2.1716.872.42现场观测1.63～3.54(约3.0～6.5×107kN)[18]——文献[19]2.60～6.58—钢轨表面

由表2可知，考虑型面磨耗时曲线外轨疲劳裂纹萌生寿命小于不考虑磨耗时的预测结果，与现场观测的结果更为接近。这时裂纹萌生于钢轨亚表面，距离轨头表面深度约2～3 mm，考虑磨耗时预测的萌生位置略靠近轨顶中心。

3 结果分析

根据表2中的裂纹萌生位置找出对应在钢轨上的位置，见图8。其中，A点为考虑钢轨型面磨耗情况下的裂纹萌生位置，P点为不考虑型面磨耗时的裂纹萌生位置。为了分析考虑磨耗时的P点疲劳损伤，假定在型面磨耗情况下该位置点为P′。

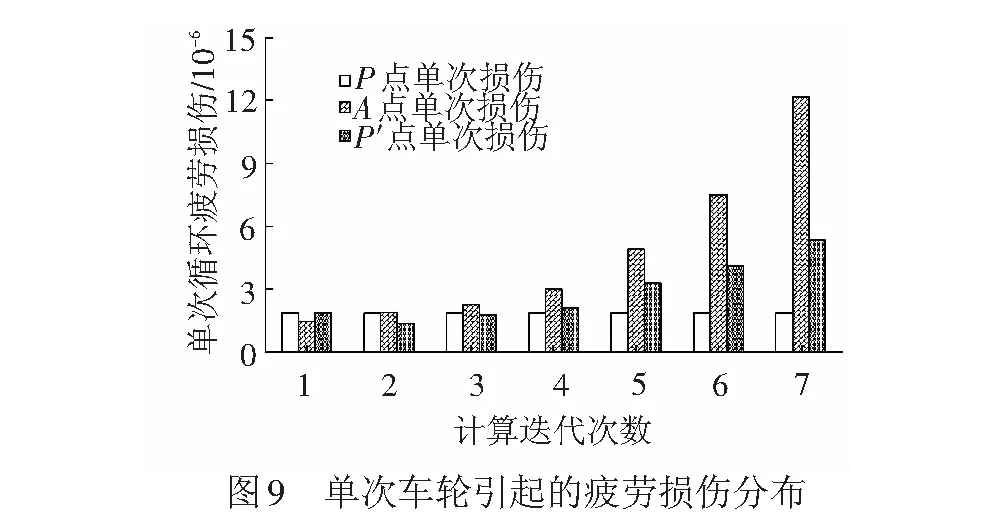
单次车轮引起的疲劳损伤分布见图9，其中横坐标表示因磨耗达到设定的磨耗量而替换型面的次数，也反映裂纹萌生前的不同磨耗阶段。由图9可知：

(1) 在标准型面时(型面第1个磨耗阶段)，P(P′)点的单次疲劳损伤大于A点的单次疲劳损伤，说明最初轮轨作用对P(P′)点的损伤较大，印证了当不考虑磨耗时，P点的单次疲劳损伤以及累积疲劳损伤都较大，裂纹最终萌生于P点而不是A点。

(2) 在第1～4个型面磨耗阶段(第4个磨耗阶段对应的车轮通过次数约为0.91×105～1.22×105，换算成通过总重约为1.67～2.24×107kN)，A点的的单次疲劳损伤都较小，但其单次疲劳损伤呈缓慢增加趋势，P′点也具有相似的规律。说明在这个时期，轮轨几何关系匹配比较好，单次疲劳损伤较小且发展缓慢，裂纹萌生相对较慢。

(3) 第5个型面磨耗阶段(车轮通过次数约为1.22×105～1.54×105，换算成通过总重约为2.24～2.83×107kN)，A点的单次疲劳损伤比P′点大49%。说明这个磨耗阶段，由于轨距角和轨肩的型面被磨损降低，轮轨接触点略向轨顶中心移动。同时，轮轨接触斑长短半轴之比略有增大，导致接触应力增加，使得A点疲劳损伤加快增长。

(4) 随着型面的进一步磨耗(第6、7个磨耗阶段)，轮轨作用关系越来越差，A点的单次疲劳损伤迅速增加，导致A点比P′点更早达到疲劳临界损伤值，因此，考虑磨耗时A点对应的车轮通过次数较不考虑磨耗时P点的车轮通过次数小约60%，A点先达到疲劳累积损伤临界值。

将每个磨耗阶段的A点和P′点单次疲劳损伤乘以对应的车轮通过次数，可以得到2点的疲劳累积损伤，再结合不考虑磨耗时P点的疲劳累积损伤(以单次损伤为斜率随车轮通过次数累积而呈线性增加趋势)，得到疲劳累积损伤与车轮通过次数的关系,见图10。

由图10可知：在第1个磨耗阶段(车轮通过次数约为0.3×105以下)，P′(P)点的疲劳累积损伤为0.055，A点的疲劳累积损伤为0.043,说明若没有磨耗，P′(P)点将以这个累积损伤达到疲劳破坏，对应车轮通过次数为5.39×105次；但是由于轮轨接触会因为型面的磨耗而发生变化，进一步导致轨头各点应力应变的变化，因此，A点和P′点的疲劳累积损伤随着磨耗逐渐增加，且A点增加得更快;到了第5个磨耗阶段(车轮通过次数约为1.22×105～1.54×105次)，A点的疲劳累积损伤为0.27，大于P′点的疲劳累积损伤0.22，并持续快速增大;最后，当A点疲劳累积损伤达到1时，P′点的疲劳累积损伤为0.62，A点为裂纹萌生点，而不是不考虑磨耗时的P′(P)点。裂纹萌生在A点时对应的车轮通过次数为2.17×105次。

综上所述，在考虑磨耗的裂纹萌生寿命预测方法中，由于考虑了型面磨耗引起的轮轨接触位置和钢轨应力应变变化，找到了钢轨内部更容易发生疲劳累积直至破坏的点，比不考虑磨耗的裂纹萌生寿命预测方法得到的裂纹萌生位置更合理、裂纹萌生寿命更接近现场观测。

4 结论

(1) 将磨耗模型和裂纹萌生预测模型相结合，根据不同的磨耗阶段分别进行钢轨应力应变计算和疲劳损伤累积，建立了考虑磨耗的钢轨疲劳裂纹萌生寿命预测方法，裂纹萌生预测更接近现场观测结果，并可分析磨耗和疲劳裂纹萌生的相互关系。

(2) 在疲劳裂纹萌生之前，磨耗使得轮轨经常接触区域的型面发生变化，造成接触斑逐渐向轨顶中心方向偏移，使得处在接触斑偏移方向的材料点的疲劳累积损伤加快，最终更早地萌生裂纹；而远离接触斑影响范围的、在不考虑磨耗时认为是裂纹萌生点的材料点则不会萌生裂纹。

(3) 预测磨耗情况下的U75V热处理钢轨在800 m半径曲线外轨时的裂纹萌生寿命约为4.5×107kN，对应车轮通过次数2.17×105次。当轮轨摩擦系数为0.3时，裂纹萌生在钢轨亚表面，距离轨顶面2.42 mm。

(4) U75V热处理钢轨在上道初期的一定阶段内轮轨关系较稳定，磨耗和疲劳裂纹发展缓慢。该阶段大约是钢轨上道至车轮通过次数约为1.22×105次，对应通过总重约为2.24×107kN。

参考文献：

[1] ZHOU Yu,WANG Shaofeng,WANG Tianyi,et al.Field and Laboratory Investigation of the Relationship Between Rail Head Check and Wear in a Heavy-haul Railway[J].Wear,2014,315(1/2):68-77.

[2] 王少锋，周宇，许玉德，等.基于蠕滑理论的钢轨临界平面疲劳参量仿真[J].铁道学报，2014,36(4):65-70.

WANG Shaofeng,ZHOU Yu,XU Yude,et al.Simulation of Fatigue Parameters of Rail Critical Plane Based on Wheel-rail Creep Theory [J].Journal of the China Railway Society,2014,36(4):65-70.

[3] RINGSBERG J W.Life Prediction of Rolling Contact Fatigue Crack Initiation[J].International Journal of Fatigue,2001,23(7):575-586.

[4] JIANG Y,SEHITOGLU H.A Model for Rolling Contact Failure[J].Wear,1999,224(1):38-49.

[5] ARCHARD J F.Wear Control Handbook:Wear Theory and Mechanisms [M].New York:ASME,1980:161-78.

[6] LI Z L,ZHAO X,DOLLEVOET R,et al.Differential Wear and Plastic Deformation as Causes of Squat at Track Local Stiffness Change Combined with Other Track Short Defects[J].Vehicle System Dynamics,2008,46(1):237-246.

[7] KALOUSEK J,MAGEL E.Achieving a Balance:The Magic Wear Rate[J].Railway Track & Structures,1997,93(5):50-52.

[8] MAGEL E,RONEY M,KALOUSEK J,et al.The Blending of Theory and Practice in Modern Rail Grinding[J].Fatigue and Fracture of Engineering Materials and Structures,2003,26(10):921-929.

[9] FLETCHER D I,BEYNON J H.Equilibrium of Crack Growth and Wear Rates During Unlubricated Rolling-sliding Contact of Pearlitic Rail Steel[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2000,214(2):93-105.

[10] DONZELLA G,FACCOLI M,MAZZA,et al.Progressive Damage Assessment in the Near-surface Layer of Railway Wheel-rail Couple Under Cyclic Contact[J].Wear,2011,271(1/2):408-416.

[11] MADGE J J,LEEN S B,MCCOLL I R,et al.Contact-evolution Based Prediction of Fretting Fatigue Life:Effect of Slip Amplitude[J].Wear,2007,262(9/10):1 159-1 170.

[12] MADGE J J,LEEN S B,SHIPWAY P H.A Combined Wear and Crack Nucleation-propagation Methodology for Fretting Fatigue Prediction[J].International Journal of Fatigue,2008,30(9):1 509-1 528.

[13] LEEN S B,HYDE T H,RATSIMBA C,et al.An Investigation of the Fatigue and Fretting Performance of a Representative Aero-engine Spline Coupling[J].Journal of Strain Analysis for Engineering Design,2002,37(6):565-583.

[14] ZHANG T,HARRISON N M,MCDONNELL P F,et al.A Finite Element Methodology for Wear-fatigue Analysis for Modular Hip Implants[J].Tribology International,2013,65(3):113-127.

[15] LI Z L,KALKER J J.Simulation of Severe Wheel-Rail Wear[C]// Proceedings of the 6th International Conference on Computer Aided Design,Manufacture and Operation in the Railway and Other Advanced Mass Transit Systems.UK:WIT Press,1998:393-402.

[16] JENDEL T,BERG M.Contact Mechanics:Prediction of Wheel Wear for Rail Vehicles-Methodology and Verification[M].Berlin:Springer Netherlands,2002:229-236.

[17] 王天一.重载铁路小半径曲线钢轨特殊型面设计方法研究[D].上海：同济大学,2014：35-40.

[18] WANG J X,XU Y D,LIAN S L,et al.Probabilistic Prediction Model for Initiation of RCF Cracks in Heavy-haul Railway[J].International Journal of Fatigue,2011,33(2):212-216.

[19] 王少锋.重载铁路钢轨疲劳裂纹萌生及路径演变规律研究[D].上海：同济大学,2014：131-136.