基于Level set方法的微观水驱油模拟分析*
2016-05-15高亚军姜汉桥王硕亮李俊键刘传斌常元昊王依诚
高亚军 姜汉桥 王硕亮 李俊键 刘传斌 常元昊 王依诚
(1. 中国石油大学(北京)石油工程教育部重点实验室 北京 102249; 2. 中国地质大学(北京)能源学院 北京 100083)
基于Level set方法的微观水驱油模拟分析*
高亚军1,2姜汉桥1王硕亮2李俊键1刘传斌1常元昊1王依诚1
(1. 中国石油大学(北京)石油工程教育部重点实验室 北京 102249; 2. 中国地质大学(北京)能源学院 北京 100083)
高亚军,姜汉桥,王硕亮,等.基于Level set方法的微观水驱油模拟分析[J].中国海上油气,2016,28(6):59-65.
Gao Yajun,Jiang Hanqiao,Wang Shuoliang,et al.Simulation analysis of microscopic water-oil displacement based on Level set method[J].China Offshore Oil and Gas,2016,28(6):59-65.
通过引入Level set方法,构建两相界面运移数学表征方法,结合Navier-Stokes方程建立两相微观渗流数学模型,借助有限元方法进行求解,并利用微观玻璃刻蚀模型驱替实验验证数值模拟结果。结果表明,基于该渗流数学模型的数值模拟结果与实验结果的吻合度很高。利用Navier-Stokes方程并结合Level set方法实现了两相流体驱替的微观数值模拟,从而为研究微观两相渗流特征及驱油机理提供了一种新方法。在不等径并联喉道单元模型基础上,进行了不同驱替条件下的数值模拟计算,分析了发生孔隙尺度两相窜流的临界喉道直径比的变化特征,结果表明驱替压差及油水两相黏度比越大,越容易发生微观窜流,更易导致在较小喉道中形成微观残余油。本文研究结果为微观水驱油机理的进一步研究奠定了基础。
数值模拟;Level set方法;微观水驱油;微观残余油
目前许多学者在微观水驱油两相流动特征方面做了大量的实验研究,实验方法主要有三维平板模型[1]、玻璃刻蚀物理模拟等,但这些实验模拟成本高,操作较为繁琐困难,并且由于实验监测技术和图像获取精度有限,导致实验数据处理误差较大。近年来,微观渗流的数值模拟方法迅速发展,已形成网络模拟和玻尔兹曼法两大类,传统模型中孔隙结构已用柱状喉道和互相连接的球状孔隙代替。Fatt[2]最早用孔隙网络模型研究多孔介质二维网格中的流体动静态问题,随后网络模型被不断改进。尽管孔隙网络模型可以很好地计算相对渗透率和残余油饱和度[3-4],但是孔喉结构太理想化,无法解释流体动态机理[5]。玻尔兹曼法可以很好模拟岩石孔隙的两相渗流,定性符合较好[6-7],但也无法刻画孔隙内部油水两相界面动态运移特征。
在微观水驱油研究中,油水两相流动特征及剩余油分布状态均是通过孔隙内油水两相界面体现出来的。在Navier-Stokes方程的基础上,计算流体动力学方法在两相流领域的模拟应用逐渐发展起来[8],所形成的两相流体相界面动态特征的研究方法主要有界面追踪类和界面捕获类,其中以Level set方法为代表的界面捕获类方法应用较多[9]。Level set方法是由Osher和Sethian提出[10],后经Sussman等和Olsson等的发展改进[11-13],保持了计算过程中的体积守恒。Level set方法在孔隙尺度油水两相流领域应用较少,仅用来模拟研究孔隙尺度下水驱和CO2驱采收率的比较及孔喉中流体相界面的动态驱替特征[14-15],而且现有文献均是直接建立孔隙模型进行数值模拟,模拟的实际精确度有待实验验证。
本文利用岩心切片扫描图像构建真实孔隙拓扑分布结构,建立二维微观孔隙模型,结合Navier-Stokes方程,用Level set方法进行数值模拟,模拟结果与可视化微观玻璃刻蚀实验结果达到高度吻合,证明了模拟结果的可靠性,克服了上述常规实验方法和模拟方法存在的诸多问题。通过此模型,模拟计算残余油富集孔道直径及孔道内流速和压力的分布特征,并在不等径并联孔道单元基础上分析在大孔道存在的情况下小孔道内原油被驱动的孔径条件,为微观孔隙驱油机理的进一步研究奠定了基础。
1 水驱实验模型
如图1所示,在光化学玻璃上雕蚀出两种不同孔隙结构的模型A和B,均为中性润湿,其中模型A孔喉大于模型B,模型A的微观孔喉非均质性也强于模型B,且模型A中部存在明显的优势渗流通道。模型A的孔隙度为30.96%,尺寸为17.45 mm×14.31 mm;模型B的孔隙度为28.91%,尺寸为15.28 mm×12.13 mm。用另一块玻璃进行粘结密封,制作成仿真岩心微观孔隙模型,然后进行水驱油实验。实验步骤如下:
1) 安装固定玻璃刻蚀模型;
2) 将模型A和B抽真空饱和原油,对应黏度分别为50 mPa·s和20 mPa·s ,并采集原油稳定后的图像;
3) 在室温下启动定压泵从模型左端注水(实验用水密度为1 g/cm3,黏度为1 mPa·s),进行水驱油过程,直到出口端基本不出油,用显微放大系统和录像机录取实验过程的图像,并用计算机图象处理系统对录像和图片进行处理。

图1 饱和不同原油的玻璃刻蚀模型
2 数学模型
建立二维几何模型,在孔隙尺度两相流动中用Navier-Stokes方程来描述微观两相流体的动量传输特性,用Level set算法来刻画在不同驱替时刻两相界面动态变化,二者联立建立微观两相渗流数学模型。其假设条件为:①孔隙内水油两相流体均为不可压缩流体,流动状态为层流;②忽略流体重力;③注入端各孔隙入口压力相等且恒定不变;④忽略玻璃刻蚀模型的厚度,流体在孔隙中属于二维流动。
2.1 几何模型
将玻璃刻蚀孔隙模型A和B在电镜下的扫描图进行二值化处理后,在AutoCAD软件中转化为孔隙轮廓图,保持模型尺寸不变。如图2所示,封闭曲线表示岩石颗粒,剩余联通区域为孔隙喉道;注入端均在右端,出口端均在左端。

图2 微观孔隙几何模型
2.2 Level set方法
在层流不可压缩非混相两相流中,用Level set方程中的φ来表示油水两相流体各自的体积分数。φ=50%时的水平集轮廓线表示两相流体相界面。对于油水两相时,油相中φ值为0,水相中φ值为100%,水驱过程中φ值可以追踪油水两相界面。因此,两相流体的界面运移方程可以表示为[16]
(1)
式(1)中:φ为油水两相界面轮廓线;γ为方程求解中的重新初始化参数;t为两相作用时间;u为流速;ε为人为设置的两相界面厚度,一般小于计算模型中网格剖分的最小单元。
借助于Level set函数φ,流体的物性可用下述方程表示:
(2)
式(2)中:ρo和ρw分别为油和水的密度;μo和μw分别为油和水的黏度。
2.3 控制方程
Navier-Stokes方程可以用于描述不可压缩流体质量和动量的传输特性。在固定的欧拉坐标系中,不可压缩且考虑界面张力的两相流动Navier-Stokes方程和连续性方程描述如下[12]:
(3)
式(3)中:ρ为密度,kg/m3;μ为动态黏度,Ns/m2;u为速度,m/s;p为入口压力,Pa;I为单位矩阵;Fst为气液界面张力,N/m。
两相流体的界面张力可以用如下连续界面力学模型中的形式来表达[17]:
Fst=σknΓδsm
(4)
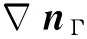
(5)
(6)

(7)
式(4)~(7)中:σ是界面张力系数;k是油水相界面曲率;nΓ是单位法向量;δsm是狄克拉函数[15]。
2.4 初始和边界条件
如图2所示,模型A右端有2个孔隙入口,左端有2个孔隙出口;模型B右端有7个孔隙入口,左端有9个孔隙出口。进出口边界压力在模型求解时设置,左右端除进出口外的边界及顶部和底部边界均为封闭边界,无流体流动。初始界面设置为t=0时水相和油相的接触面。出口和入口初始状态方程式为
(8)
(9)
孔隙壁面条件均为中性润湿,垂直壁面方向流速为0,方程式如下:
u·nwall=0
(10)
速度在壁面方向的法向分量为零,但由于壁面的润湿性,速度在壁面方向的切线分量不为零,有一个极小的速度滑移。这个极小的速度分量可用如下的附加摩擦力来表示:
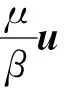
(11)
式(11)中:Ffr为摩擦力;μ为动力黏度;β为滑移长度,取值等于边界部位剖分网格的尺寸。
3 模型验证及模拟结果分析
基于上述数学模型,对这两个微观孔隙结构不同的模型进行求解,并进行数值模拟和实验结果的对比,进而分析喉道内流体流动特征。
3.1 数值模拟与实验结果对比
数学模型通过有限元方法进行求解。几何模型用自由三角形网格差分,网格剖分数分别为93 121和46 906个。初始状态孔隙中均饱和油,入口端注入水,水和油的密度、黏度及注入压力如表1所示。为了保证计算过程的收敛性及节省计算时间,入口压力与实验压力保持一致。孔隙内部初始压力均为零。将数值模拟结果与实验结果进行对比,以验证模拟结果的可靠性。
如图3、4所示,在不同含水饱和度条件下将模型A和B的驱替实验所录取的图像与数值模拟结果进行对比,发现二者驱替相界面吻合度非常高,孔道内油水前缘相界面越尖锐,渗流阻力越小;相界面曲率越小,孔隙驱替阻力越大。

表1 油水两相微观渗流平面模型相关参数
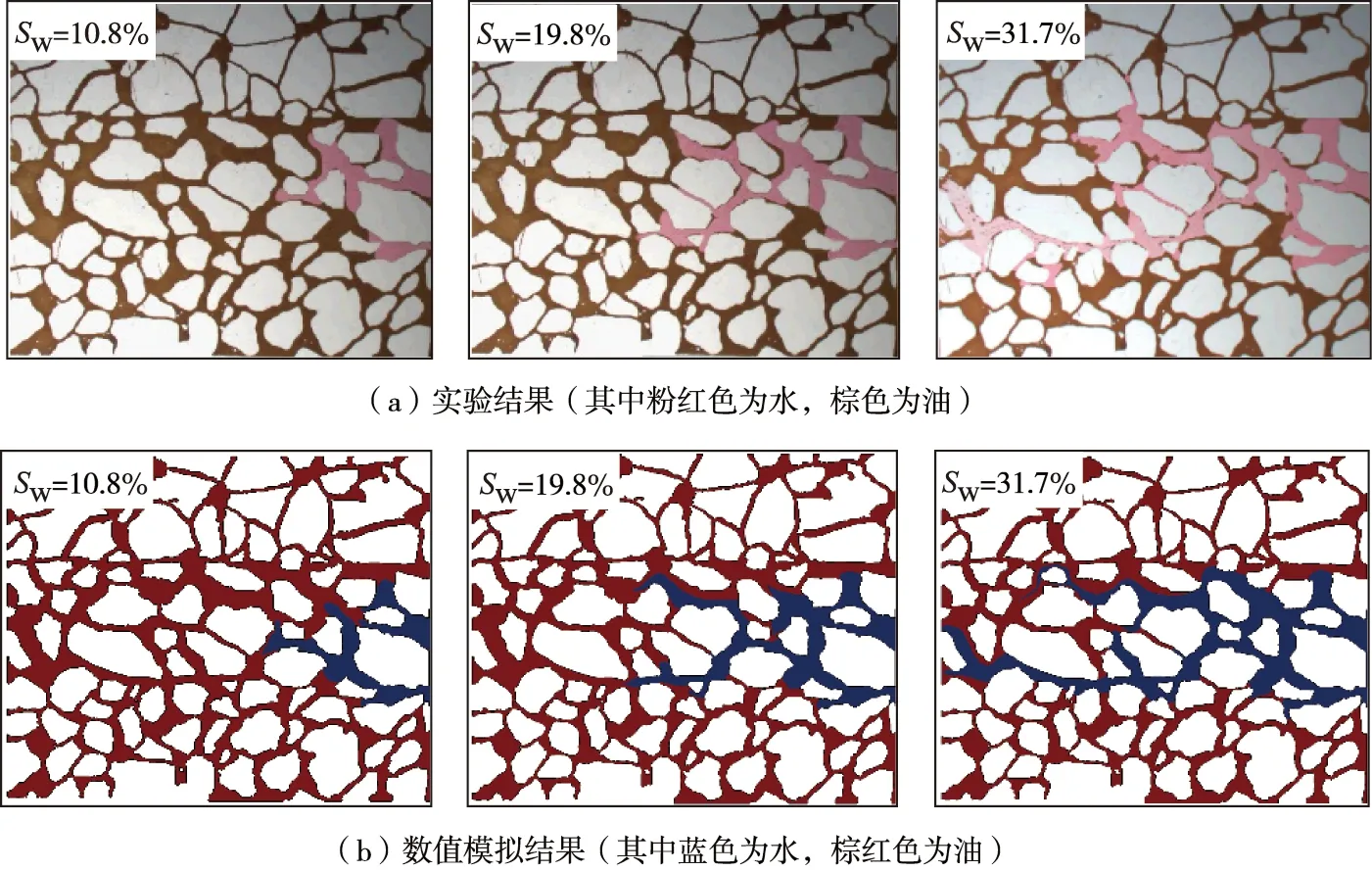
图3 模型A实验与数值模拟的结果对比

图4 模型B实验与数值模拟的结果对比
记录玻璃刻蚀实验条件下各时刻的含水饱和度,与数值模拟得到的含水饱和度在相同归一化时间下进行对比,发现二者的吻合度也很高(图5)。左端见水时,模型A与模型B的含水饱和度分别为31.7%和66.8%,与图5中曲线拐点处的含水饱和度吻合;见水后,采收率曲线变得平缓,上升幅度缓慢,水相突破后驱替阻力减小,水基本沿着主要流动通道运移,波及范围几乎不再扩大,驱油效率不再增加。模型A存在较明显窜流通道,且原油黏度较高,指进现象严重,水沿窜流通道迅速突破,模拟得出的最终驱油效率仅为41.2%;模型B孔喉分布较模型A均匀,波及效率较高,模拟得出的最终驱油效率为72.8%。
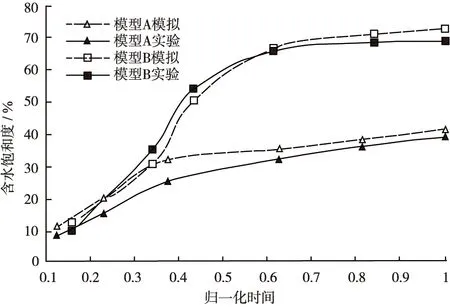
图5 实验与数值模拟的含水饱和度对比
3.2 喉道内流体流动特征分析
对模型B的驱替过程分析表明,在保持驱替压差不变的情况下,当含水饱和度达到72.8%时,流动达到稳定状态,孔隙基本不出油。取9处富含残余油的喉道,其孔隙及流体特性参数值如表2所示。喉道残余油的形成主要是由于驱替相水在垂直于喉道界面的方向动力不足,对孔喉内流体的驱动速度远小于其他喉道的平均流速,当小喉道被其它喉道率先突破的水相截断时驱动速度基本为零,喉道残余油形成。
由于所建立的孔隙模型壁面相对于实验模型较为理想光滑,模拟得到的驱替速度大于实验条件下的驱替速度。模型B在数值模拟中驱替压力梯度为内部最大瞬时流速4.407 m/s,出口最大速度1.093 m/s,出口平均速度0.289 6 m/s。从模型B整个孔隙模型驱油效果来看,残余油富集喉道内最大流速远小于出口流速,流速随喉道内驱替压力梯度的增大而增大(图6a),但与喉道直径无明显关系(图6b),因此,仅从单个孔道大小无法衡量驱油阻力大小及分析残余油的形成原因。
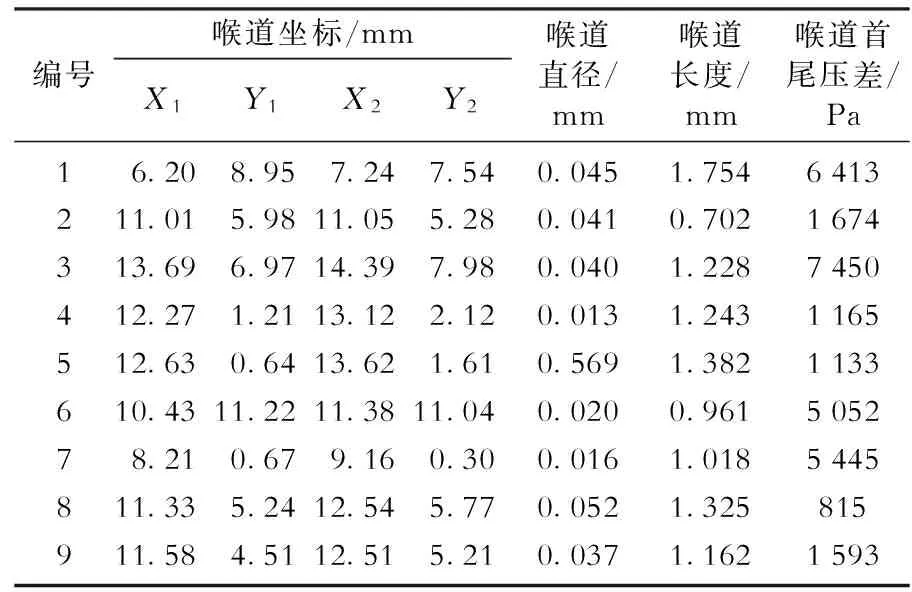
表2 模型B富含残余油喉道特性参数
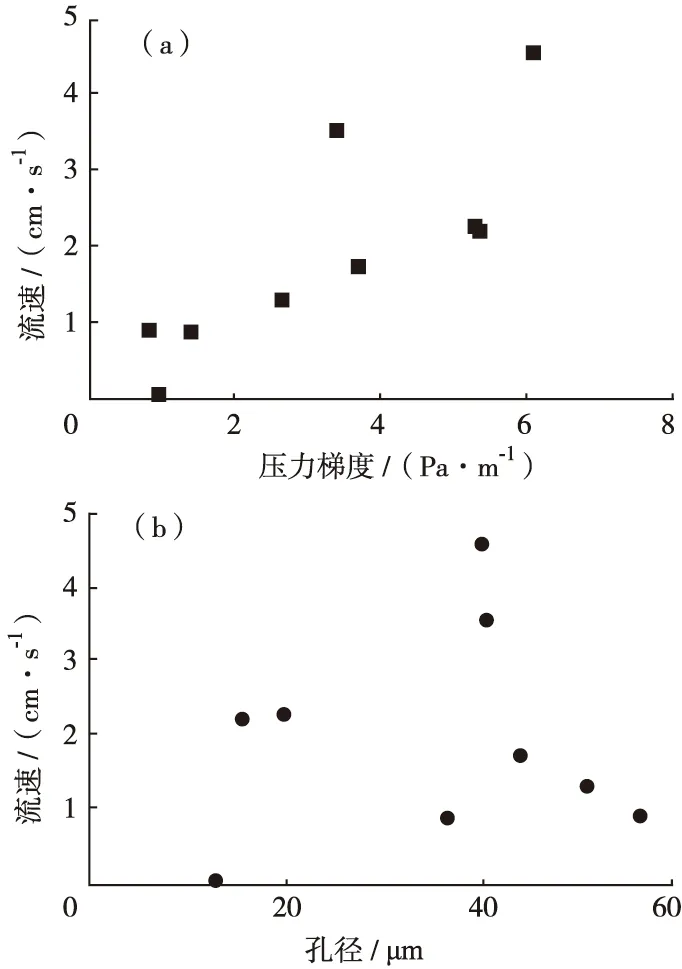
图6 模型B喉道内流速与压力梯度及孔径的关系
连接2个孔隙的喉道有多个,且可视为不等径并联喉道单元(图7)。各喉道内的驱替速度受驱油动力和油水流动阻力(即驱替压差、油水黏度比及并联各孔径比值)的相互制约。在表2中,孔隙4和5、8和9属于同一并联喉道系统。在同一并联喉道单元中,水相在流速较快的大喉道优先突破,在流速较慢的小喉道形成封堵,从而降低了喉道首尾压差,导致残余油的形成,这种现象简称为微观喉道窜流。分析认为,并联喉道直径的比值对孔道是否发生微观窜流影响很大。
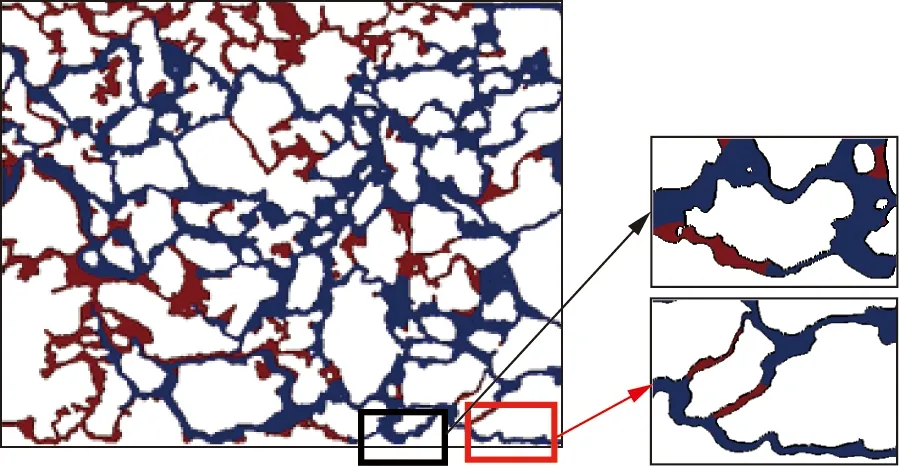
图7 模型 B中并联喉道单元示意图
为节省模型计算时间并保证数值计算的收敛性,将图7所示的模型孔隙中各个并联喉道单元中喉道直径依次近似取值为10、20、30、40、50、80、100 μm,模拟计算得出驱替压差为5 kPa时相应直径喉道内的最大流速与直径为10 μm的喉道内的流速比分别为1、3、53、154、235、500、660倍。由此可见,微观孔隙结构中,孔道的直径对孔道内两相驱替流速的影响很大。
在水驱过程中,水相随喉道直径从大到小依次突破。在模拟驱替压差为5 kPa时并联喉道水驱过程中,当30 μm直径喉道发生水相突破后,直径为10 μm及以下的喉道油水相界面基本不再向前推移,此时发生微观窜流的临界喉道直径比为3,临界流速比为53。
在改变驱替压差和油水黏度比的条件下对并联喉道单元进行模拟计算,得到不同条件下微观窜流临界喉道直径比(图8)。由图8a可以看出,当驱替压差一定时,油水黏度比越大,发生窜流的临界喉道直径比越小,即油水黏度比越大,越易发生微观窜流。由图8b可以看出,在油水黏度比一定时,驱替压差越大,发生窜流的临界喉道直径比越小,即驱替压差越大,越易发生微观窜流。
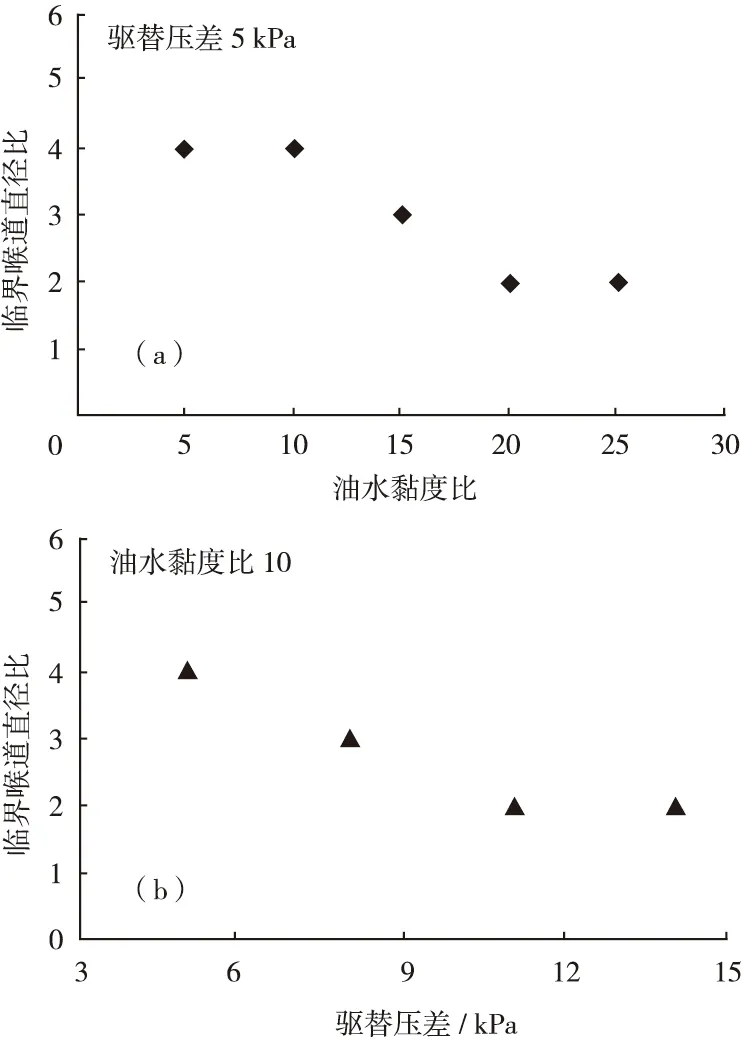
图8 模型B中油水黏度比及驱替压差对微观窜流临界喉道直径比的影响
由以上分析可以发现,微观条件与宏观条件下的窜流规律吻合。在孔隙尺度微观水驱油过程中,当驱替压差恒定时,直径较大的喉道中流体速度增加速率远大于直径较小的喉道,并且增加油水黏度比和驱替压差均不利于增加直径较小喉道中液体流速的相对增加量,因此小喉道更容易被优先突破大喉道的液体封堵,更易导致微观窜流的发生,从而在相对较小的喉道中形成残余油。
4 结论
1) 基于Navier-Stokes方程,结合Level set数学方法,进行了微观二维孔隙尺度水驱油模拟,模拟结果与实验得到的结果吻合度很高,为微观水驱油机理研究提供了新的技术思路。
2) 考虑整个模型中孔道内驱替流体流速与孔径相关性差,从不等径并联喉道单元的角度分析了微观窜流临界喉道直径比,并对不同直径喉道单元在不同驱替条件下的流动特征进行了模拟,结果表明驱替压差及油水黏度比越大,微观不等径并联喉道中发生窜流的可能性越大,更易导致在相对较小的喉道中形成微观残余油。
[1] 姜汉桥,宋亮,张贤松,等. 基于核磁共振的正韵律厚油层高含水期挖潜室内实验[J].中国海上油气,2014,26(6):40-43. Jiang Hanqiao,Song Liang,Zhang Xiansong,et al.Laboratory NMR experiments on tapping the production potential of positive rhythmic and thick oil reservoirs in high water-cut stage[J].China Offshore Oil and Gas,2014,26(6):40-43.
[2] FATT I.The network model of porous media I:capillary pressure characteristics[J].Trans AIME,1956,207:144-159.
[3] BLUNT M J,JACKSON M D,PIRI M,et al.Detailed physics,predictive capabilities and macroscopic consequences for pore-network models of multiphase flow[J].Advances in Water Resources,2002,25(8-12):1069-1089.
[4] LOVOLL G,MEHEUST Y,MALOY J K,et al.Competition of gravity,capillary and viscous forces during drainage in a two-dimensional porous medium:a pore scale study[J].Energy,2005,30(6):861-872.
[5] RAMSTAD T,IDOWU N,NARDI C,et al.Relative permeability calculations from two phase flow simulations directly on digital images of porous rocks[J].Transport in Porous Media,2012,94(2):487-504..
[6] RICHARD D.Oriented percolation in two dimensions[J].The Annuls Probability,1999 ,12(4):999-1040.
[7] 许友生,刘慈群,俞慧丹.多孔介质中两相驱离的格子Boltzmann模型新研究[J].应用数学和力学,2002,23(4): 353-358. Xu Yousheng,Liu Ciqun,Yu Huidan.New studying of Lattice-Boltzmann method for two-phase driven in porous media[J].Applied Mathematics and Mechanics,2002,23(4): 353-358.
[8] 张超,张智,曾春珉,等.涠洲11-4油田含CO2气井油管柱腐蚀分析[J].中国海上油气,2015,27(4):122-125.DOI:10.11935/j.issn.1673-1506.2015.04.018. Zhang Chao,Zhang Zhi,Zeng Chunmin,et al.Analysis on tubing corrosion for gas wells with CO2in WZ 11-4 oilfield[J].China Offshore Oil and Gas,2015,27(4):122-125.DOI:10.11935/j.issn.1673-1506.2015.04.018.
[9] 张媛,王硕亮,张贤松.微圆管实验压力误差校正方法探讨[J].中国海上油气,2016,28(2):94-98.DOI:10.11935/j.issn.1673-1506.2016.02.012. Zhang Yuan,Wang Shuoliang,Zhang Xiansong.Discussion on method for correcting the pressure error in micro tube experiment[J].China Offshore Oil and Gas,2016,28(2):94-98.DOI:10.11935/j.issn.1673-1506.2016.02.012.
[10] OSHER S,SETHIAN J A.Fronts propagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics,1988,79(1):12-49.
[11] SUSSMAN M,ALMGREN A S,BELL J B,et al.An adaptive level set approach for incompressible two-phase flows[J].Journal of Computational Physics,1999,148(1):81-124.
[12] OLSSON E,KREISS G.A conservative level set method for two phase flow[J].Journal of Computational Physics,2005,210(1):225-246.
[13] OLSSON E,KREISS G,ZAHEDI S.A conservative level set method for two phase flow II[J].Journal of Computational Physics,2007,225(1):785-807.
[14] GUNDE A,BERA B,MITRA S K.Investigation of water and CO2(carbon dioxide) flooding using micro-CT (micro-computed tomography) images of Berea sandstone core using finite element simulations[J].Energy,2010,35(12):5209-5216.
[15] ZHU Qianlin,ZHOU Qianlong,LI Xiaochun.Numerical simulation of displacement characteristics of CO2injected in pore-scale porous media[J].Journal of Rock Mechanics and Geotechnical Engineering,2016,8(1):87-92.
[16] COMSOL Inc.COMSOL multiphysics[R].Stockholm:COMSOL Inc,2014.
[17] SHEPEL S V,SMITH B L.New finite-element/finite-volume Level set formulation for modelling two-phase incompressible flows[J].Journal of Computational Physics,2006,218(2):479-494.
(编辑:张喜林)
Simulation analysis of microscopic water-oil displacement based on Level set method
Gao Yajun1,2Jiang Hanqiao1Wang Shuoliang2Li Junjian1Liu Chuanbin1Chang Yuanhao1Wang Yicheng1
(1.MOEKeyLaboratoryofPetroleumEngineering,ChinaUniversityofPetroleum,Beijing102249,China; 2.SchoolofEnergyResources,ChinaUniversityofGeosciences,Beijing100083,China)
A new microscopic two-phase seepage flow mathematic model is established and solved with finite element method, in which the movement characteristics of the two-phase interface are characterized with Level set method and Navier-Stokes equation. The numerical simulation is verified by the experiment conducted with micro etching glass model. Results show that the numerical simulation results agree well with that of physical experiment. Navier-Stokes equation combined with Level set method implements the micro numerical simulation of two-phase flow, which provides a new method to study micro two-phase seepage characteristics and oil displacement mechanisms. The simulation is carried out under different displacement conditions based on the unequal-diameter parallel pore throat unit model, and the variation characteristics of critical throat diameter ratio under pore-scale two-phase channeling conditions are analyzed. Results show that the larger the displacement pressure and viscosity ratio of the oil-water two-phase are, the easier the micro-channeling occurs, which leads to the formation of microscopic residual oil in the smaller throat. The work lays a foundation for further study of microscopic oil displacement mechanisms.
numerical simulation; Level set method; microscopic displacement; microscopic residual oil
1673-1506(2016)06-0059-07
10.11935/j.issn.1673-1506.2016.06.010
高亚军,男,在读硕士研究生,从事油气田开发研究。地址:北京市昌平区府学路18号中国石油大学(北京)研修楼A座401室(邮编:102249)。E-mail:gaoyajuncup@163.com。
王硕亮,男,讲师,2011年毕业于中国石油大学(北京),获博士学位,主要从事油气田开发方面的研究。地址:北京市海淀区学院路29号(邮编:100083)。E-mail:wangshuoliang@cugb.edu.cn。
TE312
A
2016-06-28 改回日期:2016-07-22
*国家重点基础研究发展计划“致密油高效开发油藏工程理论与方法研究(编号:2015CB250905)”部分研究成果。
