水驱气藏水侵预测经典经验关系式lnω=BlnR的适用性分析*
2016-05-15鹿克峰
鹿克峰
(中海石油(中国)有限公司上海分公司 上海 200335)
水驱气藏水侵预测经典经验关系式lnω=BlnR的适用性分析*
鹿克峰
(中海石油(中国)有限公司上海分公司 上海 200335)
鹿克峰.水驱气藏水侵预测经典经验关系式lnω=BlnR的适用性分析[J].中国海上油气,2016,28(6):40-45.
Lu Kefeng.Applicability analysis on classical empirical relation lnω=BlnRof water invasion prediction for water drive gas reservoirs[J].China Offshore Oil and Gas,2016,28(6):40-45.
东海已开发接近废弃的水驱砂岩气藏实际动态表明,被国内学者和现场油藏工程师广泛引用的水驱气藏水侵预测经典经验关系式lnω=BlnR并不完全符合气藏开发全过程。为此将水驱气藏物质平衡方程式与Fetkovich解析水域模型相结合,采用试算法实现了二者相互匹配条件下的水侵预测。采用本文试算法对水驱气藏水侵预测经典经验关系式的适用性进行了分析,结果表明经验关系式的适用条件与气藏水体倍数、采气速度、产量变化情况存在密切关系:水体倍数越大、采气速度越高,经验关系式适用的采气程度范围越宽;水体倍数有限、控制采气速度生产时,经验关系式仅适用于开发早期的短期预测;如果开发过程中进行了产量调整,将引起视相对压力与采出程度关系曲线上翘或下弯,经验关系式将不再适用。本文研究成果对水驱砂岩气藏水侵预测方法选择及水侵预测关系式的应用具有重要借鉴意义。
水驱气藏;水侵预测;经典经验关系式;适用条件;物质平衡方程式;Fetkovich解析水域模型;试算法
水驱气藏的动态预测是一个难题,已有的计算水侵量的非稳态模型,如Van Everdingen和Hurst模型[1]、Fetkovich模型[2]、Wang模型[3]等,虽具有较为严格的理论基础和宽泛的适用范围,但因计算过程过于复杂而难以推广。1998年张伦友[4]提出了水驱气藏水侵预测经验关系式lnω=BlnR,认为水侵体积系数与采出程度在双对数坐标图中为一简单的直线关系,其中常数B取值范围为B≥1,且常数B值越大,水体能量越弱。采用该经典经验关系式与水驱气藏物质平衡方程式结合,可得到视相对压力与采出程度关系Ψ=(1-R)/(1-RB),在通过已有生产史数据拟合确定出常数B值后,即可简单实现水驱气藏动态预测。之后,该经典经验关系式被国内学者和现场油藏工程师们广泛引用[5-8]。该经典经验关系式应用于东海已开发接近废弃的X1水驱气藏时发现,拟合得到的视相对压力与采出程度关系曲线和气藏实测点数据存在差异,在开发稳产阶段早期拟合较好,但在开发中后期差异较大(图1),这与气藏见水后产量递减、采气速度降低有关。气藏在通常的非稳态水侵模式下(稳态模型仅是理想假设),水侵速度的改变滞后于采气速度的改变,采气速度降低后一段时间内,水侵速度仍保持原高采气速度时的水平,这是导致视相对压力升高的主要原因。很明显,水侵预测经验关系式仅反映出采出程度对视地层压力的影响,未反映出采气速度的影响。为此,本文选择了经典Fetkovich解析水域模型与水驱气藏物质平衡方程式相结合,采用试算法实现了二者相互匹配条件下的水侵预测,并对经典经验关系式lnw=BlnR的适用性进行了分析。本文研究成果对水驱砂岩气藏水侵预测方法的选择及更好地应用水侵预测经验关系式具有重要的借鉴意义。

图1 东海X1气藏实际与经验关系式计算、本文试算法计算的视相对压力与采出程度关系曲线对比
1 方法原理
在忽略气藏压降所引起的束缚水膨胀和孔隙体积减小的情况下,水驱气藏物质平衡方程式可表示为[9]
G(Bg-Bgi)=GpBg+WpBw-We
(1)
式(1)以无因次形式表示为[10-11]
Ψ(1-ω)=1-R
(2)
依据式(2)可以判断:在水侵体积系数ω=0时为封闭气藏,视相对压力Ψ与采出程度R的关系呈斜率为-1的直线(图1中对角线);在0<ω<1时为水驱气藏,在天然水驱开发条件下ω随开采时间增长而逐步增大,相应地图1中视相对压力Ψ与采出程度R的关系曲线逐步偏离对角线(定容线)。
累积水侵量与水域的总压降成正比,水侵量的计算通式可表示为[12]
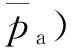
(3)
Fetkovich在引入水域产能指数的概念后实现了水侵量计算,在将预测时间划分为等时间步长的情况下,计算水域的总压降的实用关系式表示为

(4)

(5)
(6)
(7)
(8)
(9)
其中,Fetkovich水侵常数B不同于经验关系式中的常数B,它取决于水域体积、水域物性及设定的时间步长。
在已知气藏、水域相应参数的情况下,即可结合式(1)、(3)~(9)并采用试算法对气藏进行水侵预测。 具体做法为:在第1时间步末给气藏压力pf,1赋一初值,首先通过物质平衡方程式(1)计算水侵量,然后通过Fetkovich解析水域模型式(4)~(9)及式(3)计算该时间步末水侵量,若二者不等,则对pf,1重新赋值,直至二者相等,便可得到所求时间步末气藏压力pf,1值及水侵量We,1值。不断重复这一过程,按时间步依次递增的顺序可以确定出不同时间步的地层压力和水侵量。由图1可以看出,在不同开发阶段利用本文试算法所得曲线与实际曲线吻合较好。
2 经典经验关系式lnω=BlnR适用条件分析
某一典型水驱气藏基本数据为:原始天然气储量G=39.50亿m3,气藏温度T=71.11 ℃;原始地层压力p0=20.68 MPa,残余气饱和度Sgr=30%,束缚水饱和度Swi=35%,天然气偏差因子与压力的实验关系为Z=0.002 9p2-0.107 5p+1.745 4,水域有效压缩系数Ce=0.001 015 MPa-1,水域的产能指数J=1 000 m3/(d·MPa),水体倍数为100,稳产期采出程度为30%,稳产期采气速度为6%。在以下分析计算中,除选择的敏感性参数外,其他均以上述数据为准。
2.1 试算法水侵预测算例说明
已知气藏、水域基本数据,在给定的配产方案下,采用本文试算法实现水侵预测,大致分为3个步骤。
1) 采用物质平衡法计算水侵量(表1)。计算时间步长设为1 a,本算例中气藏压力对开采时间的变化是未知的。首先按压降为0.7 MPa/a给出不同时间步末初始气藏压力;然后计算得到相应压力下的气藏相对压力初始值、天然气偏差因子初始值和天然气体积系数初始值;最后采用式(1)计算得到水侵量初始值(注意此时的压力是人为给出的,所以水侵量计算结果为非真实值)。

表1 物质平衡法计算水侵量基本参数与结果
2) 采用Fetkovich解析水域模型计算水侵量(表2)。首先依据基本数据计算必需的单位压降水侵量Vace及Fetkovich水侵常数B,即
Vace=100GBgiCe=1.783 7×106m3/MPa
(10)

(11)


表2 Fetkovich解析水域模型计算初始水侵量数据
3) 采用本文试算法完成物质平衡法与Fetkovich解析水域模型法计算结果的匹配(表3)。按照前面介绍的试算方法,首先对第1时间步气藏压力重新赋值,重复步骤1和步骤2,直至第1时间步物质平衡法计算水侵量和Fetkovich解析水域模型法计算水侵量相等为止,然后进行第2时间步的试算,最终完成开发全过程的匹配。最终拟合确定的物质平衡法计算水浸量基本数据见表1,拟合确定的Fetkovich解析水域模型法计算水侵量基本数据见表3。由表1、3可以看出,两种方法拟合确定的水侵量十分接近,最终根据表1数据绘制视相对压力匹配值与采出程度关系曲线。

表3 最终拟合确定的Fetkovich解析水域模型法计算水侵量数据
2.2 敏感性参数下本文试算法与经验关系式法计算结果对比
选取水体倍数、采气速度、调整产量作为敏感性参数。对于选取的敏感性参数,首先采用本文试算法计算视相对压力与采出程度关系曲线,然后采用经验关系式lnω=BlnR对计算曲线进行拟合以确定B值,计算得到拟合曲线,二者对比确定经验关系式的适用条件。
图2为不同水体倍数时本文试算法和经验关系式法所得视相对压力与采出程度关系曲线的对比结果,可以看出:无论水体大小,两条曲线均存在一定的重合段,且重合段采出程度范围随水体倍数的增大而增大,当水体倍数从10依次增大到200时,对应曲线重合段采出程度端点由23%增大到45%,视相对压力端点均在0.8左右。进而得知,水体体积越大,经验关系式适用性越好。
图3为不同采气速度时本文试算法和经验关系式法所得视相压力与采出程度关系曲线的对比结果,可以看出:两条曲线均存在一定的重合段,且重合段采气程度范围、视相对压力范围随采气速度的增大而增大,当采气速度从2%增大到10%时,对应曲线重合段采出程度端点由17%增大到31%,视相对压力端点由0.92降低到到0.80,B值由1.25增大到1.71。进而得知,在相同水体体积下,采气速度越高,经验关系式适用性越好。结合图2及图3也可以看出,在采气速度相同时,水体倍数越大,B值越小,这与文献[4-5,8]中描述的规律一致;在水体倍数相同时,采气速度越高,B值越大,说明B值与水体能量并不是单因素关系。
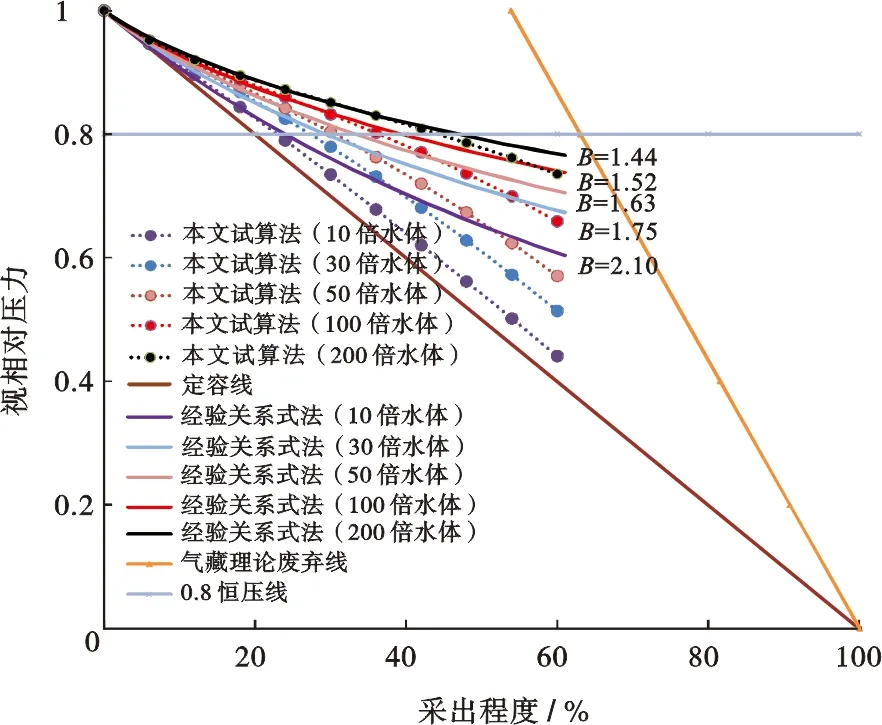
图2 不同水体倍数时本文试算法和经验关系式法所得视相对压力与采出程度关系曲线对比

图3 不同采气速度时本文试算法和经验关系式法所得视相压力与采出程度关系曲线对比
图4为气藏开发过程中采气速度改变时本文试算法和经验关系式法所得视相对压力与采出程度关系曲线对比结果,可以看出:在采气速度由6%降低到3%时,本文试算法计算曲线出现上翘;而在采气速度由6%增大到8%时,本文试算法计算曲线出现下弯。进而得知,在气藏开发过程中,人为进行产量调整或产量出现递减所导致的采气速度的改变均会引起曲线上翘或下弯,无法采用统一经验关系式进行拟合。

图4 采气速度改变时本文试算法与经验关系式法所得视相对压力与采出程度关系曲线对比
3 结论
1) 将水驱气藏物质平衡方程式与Fetkovich解析水域模型相结合,采用试算法实现了二者相互匹配条件下的水侵预测。
2) 采用本文试算法对水驱气藏水侵预测经典经验关系式的适用性进行了分析,结果表明:水体倍数越大、采气速度越高时,经验关系式适用的采出程度范围越宽;水体倍数有限、控制采气速度生产时,经验关系式仅适用于开发早期的短期预测;如果开发过程中进行了产量调整,将引起视相对压力与采出程度关系曲线上翘或下弯,经验关系式不再适用。这说明,水驱气藏水侵预测经典经验关系式的适用条件与气藏水体倍数、采气速度及产量变化情况密切相关。
符号说明

[1] VAN EVERDINGEN A F,HURST W.The application of Laplace transformation to flow problems in reservoir[J].Journal of Petroleum Technology,1949,1(12):305-324.
[2] FETKOVICH M J.A simplified approach to water influx calculations finite aquifer systems[J].Journal of Petroleum Technology,1971,23(7):814-828.
[3] WANG S W,STEVENSON V M,OHAERI C U,et al.Analysis of overpressured reservoirs with a new material equation balance method[R].Houston:SPE Annual Technical Conference and Exhibition,1999.
[4] 张伦友,李江.水驱气藏动态储量计算的曲线拟合法[J].天然气工业,1998,18(2):26-29. Zhang Lunyou,Li Jiang.Curve fitting method for dynamic reserves in water drive gas reservoir[J].Natural Gas Industry,1998,18(2):26-29.
[5] 李士伦.天然气工程[M].北京:石油工业出版社,2003:211-213.
[6] 王怒涛,黄炳光,张崇军,等.水驱气藏动态储量及水侵量计算新方法[J].西南石油学院学报,2000,22(4):26-27. Wang Nutao,Huang Bingguang,Zhang Congjun,et al.A novel method of calculating water-flooded gas in place and water influx of water drive gas reservoirs[J].Journal of Southwest Petroleum Institute,2000,22(4):26-27.
[7] 陈晖,胡泽根,王禹川.物质平衡方程在水驱气藏储量评价中的应用[J].内江科技,2011(5):112,137.
[8] 胡俊坤,李晓平,张健涛,等.计算水驱气藏动态储量和水侵量的简易新方法[J].天然气地球科学,2012,23(6):1175-1177. Hu Junkun,Li Xiaoping,Zhang Jiantao,et al.A new convenient method for calculating dynamic reserves and water influx in water driving gas reservoir[J].Natural Gas Geoscience,2012,23(6):1175-1177.
[9] 刘建仪,韩杰鹏,张广东,等.单井生产动态拟合法求取强水驱凝析气藏动态储量[J].中国海上油气,2016,28(2):83-87.DOI:10.11935/j.issn.1673-1506.2016.02.010. Liu Jianyi,Han Jiepeng,Zhang Guangdong,et al.Single well production performance fitting method for dynamic reserves of strong water-drive gas condensate reservoir[J].China Offshore Oil and Gas,2016,28(2):83-87.DOI:10.11935/j.issn.1673-1506.2016.02.010.
[10] 苏英杰,王健伟.定容凝析气藏单井凝析油污染程度判别[J].中国海上油气,2015,27(2):58-62.DOI:10.11935/j.issn.1673-1506.2015.02.010. Su Yingjie,Wang Jianwei.Identification of condensate damage degree of a well in constant volume gas condensate reservoirs[J].China Offshore Oil and Gas,2015,27(2):58-62.DOI:10.11935/j.issn.1673-1506.2015.02.010.
[11] 冯景林.基于Havlena Oden法求取水驱气藏单井控制动态储量的简便算法[J].中国海上油气,2006,18(4):255-257. Feng Jinglin.A simple method to calculate single well dynamic reserves of water drive gas reservoirs based on Havlena Odeh method[J].China Offshore Oil and Gas,2006,18(4):255-257.
[12] 李传亮.油藏工程原理[M].北京:石油工业出版社,2005:124-128.
(编辑:张喜林)
Applicability analysis on classical empirical relation lnω=BlnRof water invasion prediction for water drive gas reservoirs
Lu Kefeng
(ShanghaiBranchofCNOOCLtd.,Shanghai200335,China)
The actual dynamic data of water drive sandstone gas reservoir which is to be abandoned in the East China Sea show that the classic empirical relation lnω=BlnRof water invasion prediction widely used by domestic researchers and engineers is not applicable for the whole development process of gas reservoirs. In this paper, the material balance equation of water drive gas reservoir is combined with Fetkovich analytical model,and the water invasion under the matching condition of the two methods is predicted with trial method. The applicability of classical empirical relation of water invasion prediction for water drive gas reservoir is studied with the trial method, and the results show that the applicable conditions of empirical relation are closely related to water body multiples, gas production rate and variation of gas production rate. The larger the water body multiples and gas rate are, the broader the application range of the classical empirical relation for gas reservoir would be. When water body multiples are finite and gas production rate is restricted, the classical empirical relation can only be used in the initial stage for a short term. When production rate is adjusted, the curve of relative pressure and recovery degree will deform, and the classical empirical relation cannot be used. The research results provide reference to select water invasion prediction methods and apply water invasion prediction empirical relation for water drive sandstone gas reservoirs.
water drive gas reservoir; water invasion prediction; classical empirical relation; application conditions; material balance equation; Fetkovich analytical model; trial calculation method
1673-1506(2016)06-0040-06
10.11935/j.issn.1673-1506.2016.06.007
*中海石油(中国)有限公司综合科研项目“海上天然气稳产关键技术(编号:CCL2012SHPS0019RSI)”部分研究成果。
鹿克峰,男,高级工程师,长期从事油藏工程研究工作。地址:上海市长宁区通协路388号海油大厦(邮编:200335)。E-mail:lukf@cnooc.com.cn。
TE341
A
2016-06-08 改回日期:2016-07-14
