初中数学教材素材的加工处理
2016-05-14程锋太
程锋太

摘要:在新课程实施过程中,广大教师逐步由原来的不适应转变为课程改革的推动者,考虑到学生的差异性和课本的局限性。笔者结合农村初中的实际情况,在使用教材素材中提倡使用自主探究性素材;善于开拓约束性学习素材;重视使用情景性欢快素材;设计流动性有机素材。
关键词:新课程;初中数学教材;加工处理
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2016)02-0109
新一轮基础教育课程改革实施后,要求教师打破原有的教材观,“从教教材转变为用教材教”,在数学教学实践中正确领悟教材素材中的信息,并找出符合自己教学实际的教学素材。本文介绍笔者在教学实践中对数学素材进行加工和处理的几点做法,与大家共勉。
一、课本服从实际,提倡使用自主探究性素材
新教材的学习内容一般常用“问题情境——建立模型——解释、应用与拓展”的模式展开。但是由于地区不同,学生之间存在差异,创设问题情境时,教材中的素材不一定适用,所以针对学生的情况,可选择比教材内容更贴近学生生活,更能激发学生热情的问题作为素材。
如北师大版数学(八年级上)“一次函数”,教材选择了三个素材:摩天轮、钢管有序堆放、汽车刹车,它们分别代表了函数的三种表示方法:图像法、表达式法、表格法,这些素材的特点是:摩天轮是一种惊险的娱乐活动,它包含了重要的周期思想,可它不是一种平等的城乡都适用的数学素材,况且它的潜在的危机使家长们一般会制止学生体验;钢管有序堆放是一个探究性教学素材,对本节内容的展现速度慢,不利于概念的巩固;刹车问题是关注生命的人性化素材,是一个值得尊重的数学教材,它具备了很强的德育功能,但不可体验。如果就按教材中的三个素材教学,课堂反应平淡,任你教师激情四射,学生就是不为你“心动”。
事实上,生活中无处不包含函数思想,同学们返校途中的路程与时间的变化关系对任何一名同学都是“平等”的数学素材,通过他们自己对这一个过程的描述,既可以直接体验常量变量间的抽象关系,又可以认识到函数三种表示形式的统一性。鉴于以上认识,笔者在授课时对素材作了如下变更:
请你按要求描述你从家到学校的过程中,路程随时间的变化关系:1. 用数学语言描述早上你从家到学校的过程;2. 当你骑车的速度为15千米/时时,用表格表示你离家路程s与时间t的关系;3. (展示准备好的s-t的图象),对于给定的时间t,你能从图像中找出相应的s吗?4. 你能确定离家的路程s与时间t的关系式吗?请根据关系式计算当时,相应的s的值。
一个很小的改变,却让课堂“走”的很顺畅:它让学生走进了自主探究性学习的天空,让数学走近了生活,同时学生在“走”中亲历了现实生活情景,感受数学的美。
二、合情面对教材,善于开拓约束性学习素材
教育家杜威认为学生是起点,教材是终点,只有把教材引入学生的生活实际,让学生自己直接体验,才能把起、终点联系起来,使学生从起点走到终点。新的数学教材中有的课题标题生活化后,反而造成了学习素材的约束性.如北师大版数学(九年级上)“利用相似三角形测高”,它是一节利用相似三角形的有关知识测量旗杆的高度的活动课,课本介绍了“利用阳光下的影子”“利用标杆”“利用镜子的反射”三种方法。笔者通过教学比较发现,如果课堂内抛开书本上三个教学素材的约束,学生的思维与测量会呈现多维化的趋势。
1. 三个课本上的案例结束后,用课件展示图片:旗杆的影子不全在水平地面上,而是有一部分在其他建筑物上(如图1所示),边上有个小朋友在边挠头边自言自语,怎么办?
一个小组用课本与铅笔拼出类似图2的示意图,并给出了解决方案:太阳光线AB∥CD,墙面BC平行旗杆AO,且墙面BC垂直旗杆影子OC(如图2所示),即四边形ABCD是平行四边形,所以BC=AD。根据影长OC,测出旗杆OD部分的长,再用标杆测出影子BC,则旗杆高OA=BC+OD。
2. 同学们讨论了旗杆的斜面上的测量方案后,课件再展示一个测量小组在雨天遇到的麻烦:这天气,偏下雨,没有阳光怎么测量?
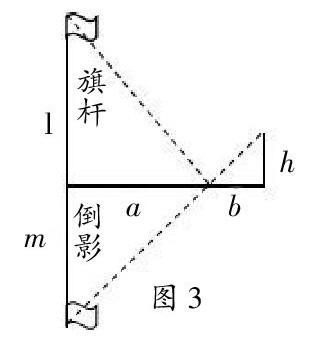
当笔者要求同学们给予帮助时,另一个学习小组马上给出了方案:雨天,路面上的小坑必会有积水(如图3),旗杆的水中会有倒影,测量者通过积水看旗杆的倒影的顶端,分别测得旗杆和观察者到积水点距离a、b,利用相似三角形的性质,得a/b=m/h且l=m,所以旗杆高度l=ah/b。
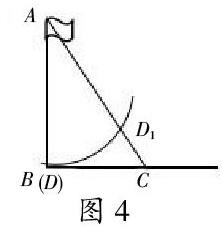
3. 临近活动结束,课件抛出“奇思妙想:你能只用一根只有2米长的皮尺测出旗杆的高度吗?”本来这是留给学生课后思考的问题,但课堂中学生强烈地解决问题的欲望使得课堂在延续中不自觉地拖堂了,可学生的解决方案马上出来了:旗杆肯定有一条长于旗杆的旗绳如图4,设表示旗杆的高度,先固定好从杆顶到杆底的绳长,并作好标记,记为AD,那么AD=AB再拉着旗绳沿水平面向前走长BC,设旗绳总长是AC,且AC=AD1+D1C,其中AD1=AB=AD,测出BC=m,CD1=n,由勾股定理得AC2=BC2+AB2,所以(AB+n)2=AB2+m2,解之得,旗杆高度AB=m2-n2/2n活动结束,学生兴致犹在,喋喋不休。
三个补充,三次发展,学以致用,体现了学生可贵的开拓精神。可见,在教学中,只要给学生一点空间,他们就会把它放大,这就是实践与创新,这才是学有价值的数学。
三、审视学习动机,重视使用情景性欢快素材
《数学课程标准》指出了数学课程从学生已有的生活经验出发让学生在已有的认知基础上体验和理解数学知识、数学素材的设计要真切感人,能够触动学生的内心深处,立即吸引学生的注意力,促进学生学习情绪的高涨,进入思维活跃的状态。
例如北师大版数学(七年级上)“求代数式的值”是一节比较枯燥的内容,可以设计让全体学生参与的“猜扑克游戏”。课前,让每名学生准备一副扑克牌。上课时,先请学生用手帕把教师的眼睛蒙起来,由教師发布指令,学生在各自的课桌上的操作:
1. 每人把一部分撲克牌分成数目相等的三堆(设此时每堆扑克牌数为张);
2. 从左边的一堆取出6张放入中间一堆;
3. 再从右边的一堆取出3张放入中间的一堆;
4. 从中间的一堆取出与左边一堆剩余张数相等的扑克牌放入左边一堆。
当全体学生操作完毕,教师立即说:“现在你们每人的中间一堆扑克牌都是15张。”学生很惊讶:“每人的牌数原来并不相等,为什么中间一堆都剩余15张而老师又能脱口而出?”学生心存疑虑,很想让教师再重复一次。于是,教师变更指令:大家先从左边的堆取出10张放入中间的一堆,再从右边的一堆取出8张放入中间的一堆,最后从中间的一堆取出与左边一堆剩余张数相等的扑克牌放入左边一堆。完毕,教师宣布:每人中间的一堆都有28张扑克牌,顿时,学生情绪高涨.教师引导学生将上述指令译成数学语言,让学生算出两次中间的一堆剩余的扑克数,分别是x+6+3-(x-6)=15张和x+10+8-(x-10)=28张。学生恍然大悟。
四、辩证看待过程,设计流动性有机素材
许多教师在使用教材时,把注意力放在调换教材内容或活动设计上。为活动而活动,为体验而体验,轻率、刻意地去更改教材素材,这是教师在使用教材中应该注意的首要问题。教师在对素材进行调整的时候,首先要对课程标准、教材进行充分的研究,完全领会教材编排的意图,对教学目标能够准备把握。
例如,北师大版数学(年级七上)“多边形和圆的初步认识”有这样一个问题:从一个多边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成多少个三角形?挖掘教材资源后进行如下设计:
1. 通过动手,你得到了怎样的规律?
学生经过动手操作,发现了几个规律:(1)多边形的边数越多,分割成的三角形越多;(2)多边形的边数每增加一边,分割成的三角形就多一个;(3)分割成的三角形个数=多边形边数-2;等等。
2. 引申:还可如何取点、连线,也可分割成若干个三角形,由此又能得到怎样的规律?
3. 从一个圆的圆心出发,引n条不重合的半径,圆被分割成多少个扇形,学生通过上题的活动经验,马上得出结论。
4. 动手设计、创意:用圆、多边形等你所熟悉的图形拼成一个漂亮的图案,并写出贴切的解说词。
学生想象丰富,设计作品多种多样,解说词更是各有千秋。
对教材素材,改造后的素材,内容丰富、趣味性强,“由此及彼”型有机的流动过程使探究目标明确,师生交流和谐。
(作者单位:江西省浮梁县王港学校 333400)
