试析证明三角形全等的技巧

刘安建

【摘 要】全等三角形是初中平面几何知识中最为重要的部分，也是中考的必考内容。通常情况下，初中几何都会通过角边角、边角边、边边边、角角边四种基本判定定理来求证三角形全等，而本文则分析了利用两个关键、三类图形和两种方法来证明三角形全等的技巧，希望可以帮助中学生丰富解题手段，更深层次了解三角形全等的解题技巧。

【关键词】三角形全等 证明 两大关键 三类图形 两种方法

一般来说，证明三角形全等就是证明三角形的角和线段相等，这也是初中平面几何的基础理论。所以说，以多角度学习证明三角形全等的方法就是学好初中平面几何的关键，对后续更复杂的几何知识学习也很有帮助。

一、证明三角形全等的两大关键

三角形全等的基本理念就是找准角与角、边与边之间的对应关系，所以本文针对三角形全等证明归纳两大关键要点：

第一，全等三角形的公共边一定要是对应边，而其公共角即对顶角也必须全是对应角。

第二，在全等三角形中，相等的边边关系所对应的角也必须为对应角；反之，相等的角其所对应的边也一定是对应边，如此才能成立三角形全等这一结论[1]。

二、证明三角形全等的三类图形

在初中平面几何教学中，通常认为的全等三角形图形形态应该包括三种：

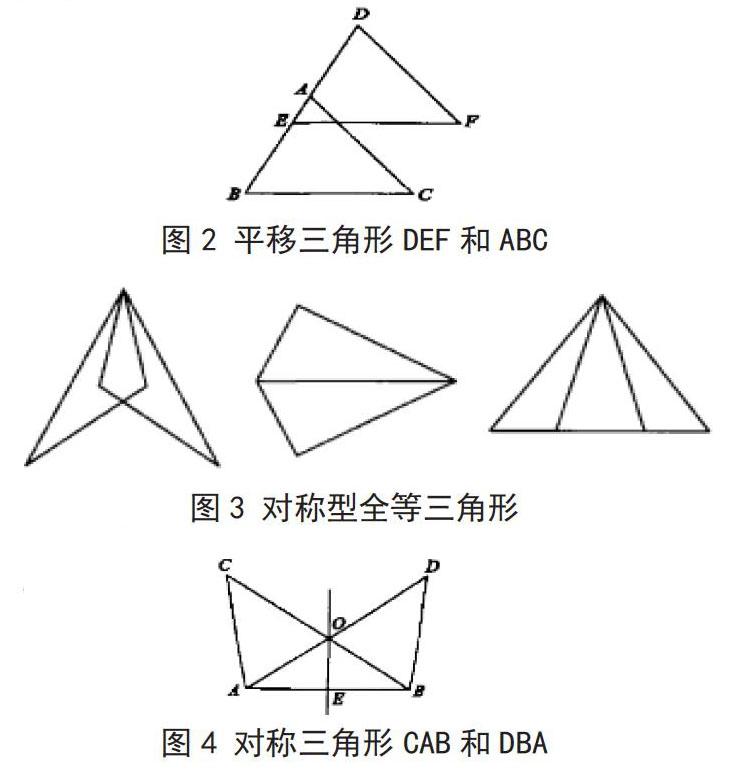
（一）平移型全等三角形

图1 平移型全等三角形

如图1中所示的即为平移型全等三角形，两个三角形在平移后依然是保持全等关系不变的，以下举例来说。

例1：如图2，在两个三角形△DEF与△ABC中，如果边EF∥BC，且有 ∠EDF=∠BAC，已知边DE=AB=8，AC=12，BC=10，那么边EF的长度为多少？

图2 平移三角形DEF和ABC

因为△DEF与△ABC符合ASA判定定理，∠EDF=∠BAC且AB=DE=8，那么BC=10，所以就有EF=BC=10.

（二）对称型全等三角形

图3 对称型全等三角形

例2：如图4，已知∠DBA=∠CAB，边DB=CA，DA与CB的相交点为O，而E为AB边的中点，试证明OE与AB的位置关系.

图4 对称三角形CAB和DBA

首先，根据ASA判定定理可以得知，因为∠DAB=∠DBA，所以△DBA与△CAB应该为全等三角形，E为AB边的中点，所以OB=OA，∠OBA=∠OAB，所以边OE与边AB应该呈垂直关系，即OE⊥AB.

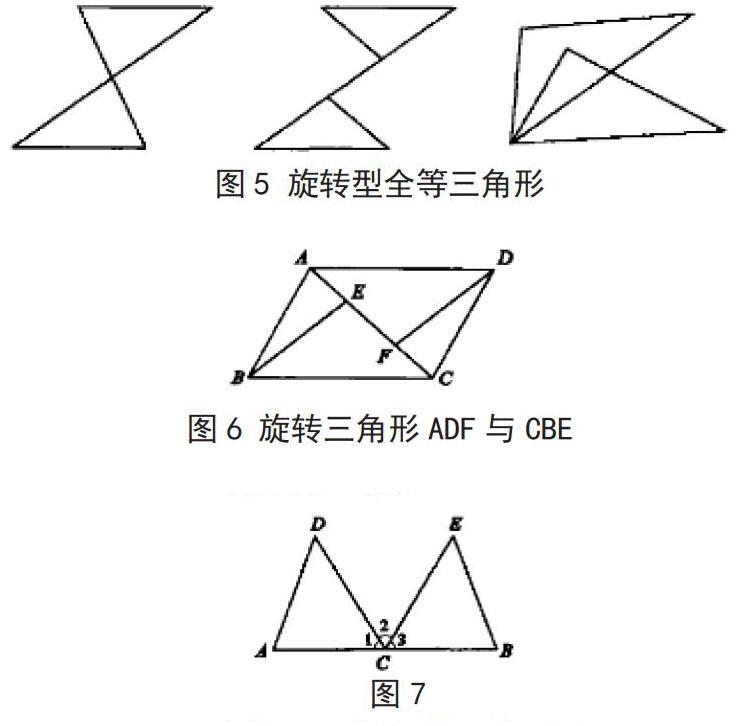
（三）旋转型全等三角形

图5 旋转型全等三角形

例3：如图6，在平行四边形ABCD中，E、F两点位于对角边AC之上，如果AF=CE，求问DF与BE边的关系.

图6 旋转三角形ADF与CBE

该题求解的是DF与BE两边的关系，从经验来看，两边应该属于平行关系，若想证明DF∥BE，就必须先证明△ADF与△CBE为全等三角形。因为AD∥BF，且AD=BC，∠DAC=∠BCA，AF=CE，所以根据SAS判定定理，可以证明△ADF与△CBE为全等三角形。在证明两三角形全等后，就可以得出结论，边DF=BE，且两边也是平行关系，DF∥BE.

以上三种图形就是在对称、平移和旋转状态下的三种全等三角形，对它们的判定还是要基于四大判定定理，并通过变换图形的角度、位置、垂直平行关系来证明它们可能存在的全等关系。对于初中生来说，它的难点就在于要用角度变换的思维来看待对三角形全等的证明，并学会灵活运用三角形全等的四个判定定理进行证明[2]。

三、证明三角形全等的两种方法

在初中平面几何学习中，对三角形全等的证明存在顺推和逆推两种方法，本文将做出一一解析。

（一）顺推分析法

所谓顺推分析自然是从已知条件出发，利用上述提到的四种判定定理或其他平面几何知识进行推导，再联系结合题目中的已知条件来发展推理过程，最后得出结论。

例4：如图7，线段AB中点为C，其中DC边平分∠ACE，有∠1=∠2，EC边平分∠BCD，有∠2=∠3，且EC=DC，证明△DAC与△EBC为全等三角形.

图7

该题目中所给出的已知条件十分充分，因为C点为线段AB的中点，所以CA=CB。因为DC、EC边平分∠ACE与∠BCD，所以∠1=∠2=∠3。又因为DC=EC，根据SAS判定定理，至此可以说明△DAC≌△EBC.

（二）逆推分析法

逆推分析法是从结论入手的解题方法，它所分析的是到达结论的可行性路径，并且根据结合所给出的已知条件和结论来寻找到正确的证明方法。在三角形全等的求解过程中，逆推分析法是十分常见的。

例5：如图8，已知BA=CA，DA=EA，请求证BD=CE.

∵DA=EA，BA=CA

∴∠C=∠B，∠1=∠2

根据SAS，∵∠B+∠3=∠1，∠C+∠4=∠2

∴∠3=∠4

DA=EA，BA=CA，∴可得△BAD≌△CAE，∴BD=CE.

以上为顺推分析和逆推分析的例题求证，如果能够娴熟掌握上述两种方法技巧，学生还可以结合顺推与逆推，用两种技巧共同解决习题，求证三角形的全等关系[3]。

四、总结

除上述解题方法外，利用公共边、公共角、对顶角等方法也能证明三角形的全等关系。因此可以说，初中平面几何中三角形全等的求解方法是丰富多样的，教师在教学过程中应该在扎实掌握四大判定定理、边角关系的基础理论的基础上，充分打开学生的思路，开阔学生的视野，从不同角度、不同层面来启迪和开发学生的解题能力。而三角形全等证明问题作为初中平面几何的基础知识，也应该被学生所熟悉运用，这对他们未来面对和解决更复杂的几何题型很有帮助。

【参考文献】

[1]娄菊红.浅谈证明三角形全等的一些技巧[J].中学生数理化（八年级数学人教版），2012（07）：6-7.

[2]钱燕群.三角形全等的证明及应用举例[J].读写算（教育教学研究），2011（08）：118-119.

[3]王志玲.八年级学生学习全等三角形推理与证明的错误分析[D].漳州：闽南师范大学，2015.