探秘几何概型题的“比例法”
2016-05-14石成效
石成效
与长度有关的几何概型
例1 在区间[[-1,1]]上随机取一个数[x],[cosπx2]的值介于[0]到[12]之间的概率为 .
分析 在区间[[-1,1]]上随机取任何一个数都是一个基本事件.所取的数是区间[[-1,1]]上的任意一个数,基本事件是无限多个,而且每一个基本事件的发生都是等可能的. 因此,事件发生的概率只与自变量[x]的取值范围的区间长度有关,符合几何概型的条件.
解 在区间[[-1,1]]上随机取一个数[x],即[x∈[-1,1]].
要使[cosπx2]的值介于0到[12]之间,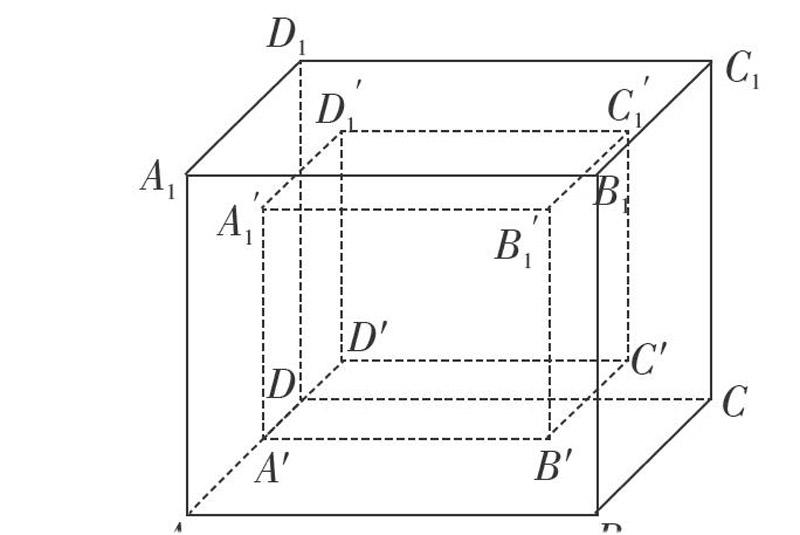
只需[-π2≤πx2≤-π3]或[π3≤πx2≤π2].
∴[-1≤ x≤-23]或[23≤ x≤1],区间长度为[23].
由几何概型知,[cosπx2]的值介于0到[12]之间的概率为
[P=符合条件的区间长度所有结果构成的区间长度=232=13].
点拨 从本题可以看出,我们将每个事件理解为从某个特定的几何区域内随机地取一点,该区域中每一点被取到的机会都一样;而一个随机事件的发生,则理解为恰好取到上述区域内的某个指定区域中的点,这样的概率模型就可以用几何概型来求解.
与角度有关的几何概型
例2 在[Rt△ABC]中,[∠A]=30°,过直角顶点[C]作射线[CM]交线段[AB]于[M],求使[|AM|>|AC|]的概率.
分析 如图所示, 因为过一点作射线是均匀的,所以应该把在[∠ACB]内作射线[CM]看作是等可能的. 基本事件是射线[CM]落在[∠ACB]内任一处,使得[|AM|>|AC|]的概率只与[∠BCC′]的大小有关,这符合几何概型的条件.
解 设事件[D]为“作射线[CM],使[|AM|>|AC|]”.
在[AB]上取点[C′]使得[|AC′|=|AC|].
因为[△ACC′]是等腰三角形,
所以[∠ACC=180°-30°2=75°,]
[μA=90°-75°=15°, μΩ=90°,]
[P(D)=15°90°=16.]
点拨 几何概型的关键是选择“测度”,如本题以角度为“测度”,其原因是射线[CM]落在[∠ACB]内的任意位置是等可能的. 若以长度为“测度”,就是错误的,因为[M]在[AB]上的落点不是等可能的.
与面积有关的几何概型
例3 在区域[x+y-2≤0,x-y+2≥0,y≥0]内任取一点[P],求点[P]落在单位圆[x2+y2=1]内的概率.
分析 应用几何概型的概率计算公式[P(A)=][d的测度D的测度],即可解决此类问题.
解 区域为[△ABC]内部(含边界).
则概率为[P=S半圆SΔABC=π212×22×2=π4.]
点拨 几何概型的概率计算公式中的“测度”,既包含本题中的面积,也可以包含线段长度、体积等,而且这个“测度”只与“大小”有关,而与形状和位置无关.
与体积有关的几何概型
例4 半径为1的球在长、宽、高分别为10,8,6的封闭长方体盒内随意飘动,则球遮住长方体的体对角线中点的概率为 .
分析 如图,题中的基本事件为球,而每个球对应一个球心,即每个基本事件对应一个球心,这些球心形成长为8、宽为6、高为4的长方体. 而球需遮住长方体对角线中点的基本事件对应点形成半径为1的球体.
解 球心移动的空间体积为
[VABCD-A′1B′1C′1D′1]=[(10-2)(8-2)(6-2)=8×6×4].
而球遮住长方体对角线中点的球心移动的空间体积[V球=4π3].
所以球遮住长方体的体对角线中点的概率为
[P=V球VABCD-A′1B′1C′1D′1=4π38×6×4=π144].
点拨 一般来讲,基本事件是线段要转化为基本事件是线段端点或线段端点与角度组成的点;基本事件是圆要转化为基本事件是圆心的点;基本事件为球要转化为基本事件是球心的点.
一般地,利用“比例法”解决几何概型题的步骤如下:(1)分析基本事件是什么,是什么非质点;(2)利用非质点与质点的一一对应关系,把基本事件为非质点问题转化为基本事件为质点问题,且转化后的基本事件出现的可能性相等;(3)根据这一点形成的区域为长度(面积、体积)求概率.
[练习]
1. 已知函数[f(x)=x2-2ax+b2],[a,b∈R].
(1)若[a]从集合{0,1,2,3}中任取一个元素,[b]从集合{0,1,2}中任取一个元素,求方程[f(x)=0]有两个不相等实根的概率;
(2)若[a]从区间[0,2]上任取一个数,[b]从区间[0,3]上任取一个数,求方程[f(x)=0]没有实根的概率.
2. (布丰投针试验)平面上画着一些平行线,它们之间的距离都等于[a],向此平面任投一长度为[l]([l]≤[a])的针,试求此针与任一平行线相交的概率.
[参考答案]
1. (1)[P(A)=612=12]
(2)[P(B)=SMSΩ=46=23]
2. [2lπa]
