浅析初中数学习题改编

陈晚珍

习题的改编，指教师改变题目中的背景条件、结论、题型、考查的重点知识等多种途径，将学生易错或是难以理解的知识点、解题方法或解题思想改编成其它的习题。现将一些编题方法作如下阐述：

一、改变图形的位置，变成同类型的新题

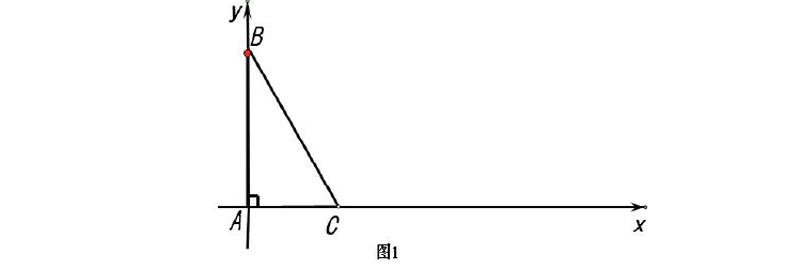
例如：原题：如图l，已知Rt△ABC的位置如图所示，点A的坐标为（0，0），点B的坐标为（0，4），点c的坐标为（3，0），将Rt△ABC沿x轴向右作无滑动的翻转，当点A第一次回到x轴时为A1，则A1的坐标为。此题可做如下的改编：

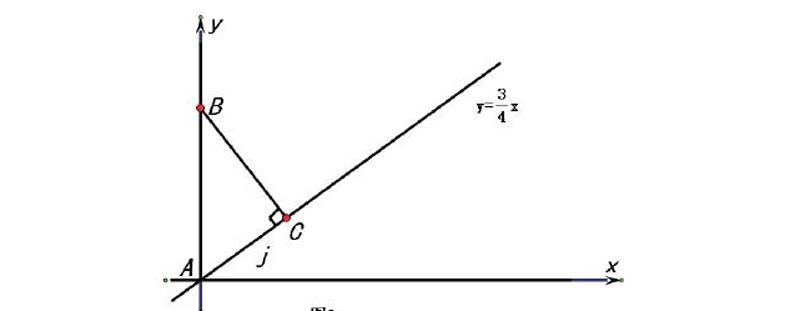
已知Rt△ABC的位置如图3所示，点A的坐标为（0，0），点B的坐标为（0，5），点c在直线y=0.75x上，且AC=3，将Rt△ABC沿直线y=0，75x向右上作无滑动的翻转，求点A再次回到直线y=0.75x时，点A1的坐标为。

通过这组编题训练，学生不仅能加深基础知识的理解和掌握，对课堂上所用知识和方法加以梳理、概括，纳入知识方法体系，还可以激发学生发现和创造的强烈欲望，发展学生的创造性思维。

二、改变题目的背景条件，改变题型（把选择题改为解答题，或是改为填空题）

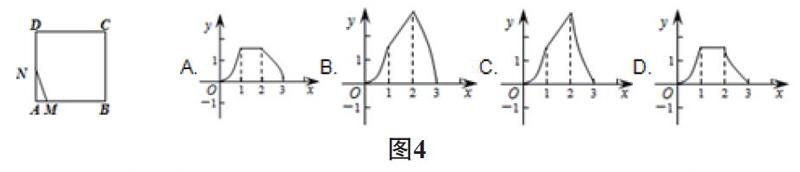
原题：如图4，在正方形ABCD中，AB 3cm，动点M自A点出发沿AB方向以每秒1cm的速度运动，同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动，到达B点时运动同时停止.设△AMN的面积为y（cm2）.运动时间为x（秒），则下列图象中能大致反映y与x之间函数关系的是（

）

这类题抽象、复杂，学生难以理解，如果只是就题讲题，学生对这类题的解法理解是不透的，我们可作如下的改编：

如图5，在矩形ABCD中，AB=8cm，BC=4cm。动点M从点A出发沿AB方向以每秒1cm的速度运动，同时动点N从点A出发，沿折线AD-Dc-CB以每秒2cm的速度运动，到达点B时同时停止运动。

（1）设△AMN的面积为s，运动时间为t，请写出S与t的函数关系式。（2）在（1）的条件下，当t为何值时，s最大？最大值是多少？（3）当点N在DC边上运动，问t为何值时，△AMN是等腰三角形？（也可以换成△AMN是直角三角形？）

学生通过做这样的习题，强化了对动点问题的解题方法的认识和理解，思维得到了训练。如果学生答题顺利，我们还可以再编，逐渐把知识纳入到问题中。

三、更换题中的某个图形，增加思维的深度和广度，形成由易到难的题组

原题：如图6，△ABc是正三角形，曲线CDEF叫做正三角形的

渐开线，其中弧CD、弧DE、弧EF的圆心依次是A、B、C。

如果AB=1，那么曲线CDEF的长是？

通过计算，我发现，每条渐开线的弧长是由半径（跟正多边形的边长有关）和圆心角（多边形的外角）决定的。因此，也可以把条件“正三角形ABC”换成“正方形”、“正五边形”甚至是“正n（n>3）边形”。也能变成规律题。

总之，改编习题教学不为形式不同的表象所迷惑，有助于学生掌握数学的本质特征，有助于扩展思维的深度和宽度，培养思维的发散能力。教学实践证明，这种方式的教学有利于克服“题海战术”的重复训练倾向，从而减轻学生的过重负担，真正实现高效教学。