构建创新能力培养的流体力学教学体系

张明辉　陈庆光

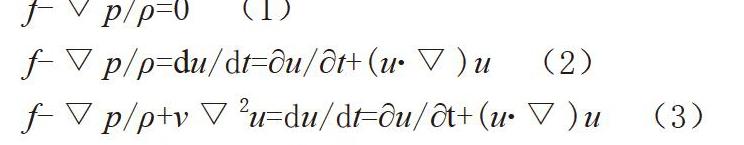
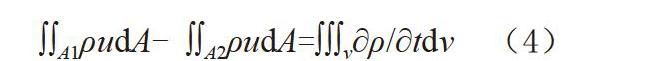
摘 要 从培养学生创新能力出发，对流体力学教材重新整合，建立树型结构教学内容体系，并提出多层次理论知识教学模式，采用不同的方法、不同的视角对流体力学的概念和方程进行解释或推导，教会学生运用联系和发展的观点学习流体力学理论，提高学生综合运用知识的能力，为发展学生的科学想象力和创造力提供更为广阔的空间。

关键词 流体力学；树型教学体系；多层次理论知识教学模式

中图分类号：G642 文献标识码：B

文章编号：1671-489X（2016）06-0075-03

Abstract In order to stimulate students cultivate the innovative ability， the teaching material of Fluid Mechanics is integrated. The tree structure of teaching system is established. The model of multi-level theory teaching is put forward. The concepts and equations of fluid mechanics are explained or deduced using different methods and different perspective. Let students study fluid mechanics theory using the view of relation and development. The students comprehensive ability to use knowledge is improved. Wider space is provided for the development of students science imagination and creativity.

Key words fluid mechanics； tree structure of teaching system； multi-level theory teaching mode

1 前言

流体力学作为一门理论性和工程实际意义都较强的专业基础课程，在一系列重要工程领域如航空航天、环境、水工建筑、流体机械、生物、化工流程等领域内发挥着支撑性基础作用，流体力学课程的教学效果直接影响本科学生的综合素质。因此，许多教育工作者从激发学生的创新意识、启发创新思维、培养创新能力出发，在流体力学课程内容选择、教学方法和教学模式、专题实验研究等多个方面进行了探索，积累了丰富的经验，取得不少成果。如：文献[1]针对工程流体力学课程内容知识点繁多、枯燥的特点，将教学内容分为七大模块，根据每个模块实际，制订有关教学方案；文献[2]提出采用“启发式”和“参与式”的多元化课堂教学方法，利用多媒体技术制作教学素材库和创建课程网站的立体化辅助教学手段改善教学效果；文献[3]提出“对比分析式”和“多视角”的课堂教学方法，教会学生运用他们拥有的知识和能力去正确比较、分析、综合、判断、概括、归纳和解决问题；文献[4]针对流体力学实验课程教学现状及存在的实际问题，提出把流体力学实验课设为一门独立课程列入专业教学计划，提升实验教学地位，建立“实验与理论并重”的新型教学观念。

本文针对山东科技大学本科生教育的特点，确定流体力学教学内容改革的方向，建立多层面素质教育的目标体系。一方面在透彻理解教材内容，明确各章节逻辑关系的基础上，找到教学的主线，将授课内容划分成树型结构，树型教学内容体系能确保在教学时概念清晰、思路明确，也方便教师依据授课学时对知识点进行删减；另一方面提出多层次理论知识教学模式，采用不同的方法、不同的视角对流体力学的概念和方程进行解释或推导，以便开阔学生思路，加深学生对重要流体力学概念和方程中各项所代表的物理含义的理解。教会学生运用联系和发展的观点学习流体力学理论，提高学生综合运用知识的能力，为发展学生的科学想象力和创造力提供更为广阔的空间。

2 建立树型结构教学内容体系

在山东科技大学，由于各专业流体力学的教学大纲要求不尽相同，因此授课学时也不相同，而教师一般都承担多个专业的教学任务。为确保学生在对简单知识充分了解和掌握的基础上，能够更容易接受相关的扩展和推广的知识点，同时减轻教师的备课负担，经过多年的教学实践，笔者总结了一套行之有效的教学方法。即在透彻理解教材内容，明确各章节逻辑关系的基础上，将授课内容划分成树型结构，每一章是枝叶茂盛的流体力学知识的一个分支，而每一章又有一个小的主干支撑。在教学时，教师依据教学大纲，找到教学的主干和分支点，合理安排教学内容，可以做到概念清晰、思路明确、重点突出、层次分明。

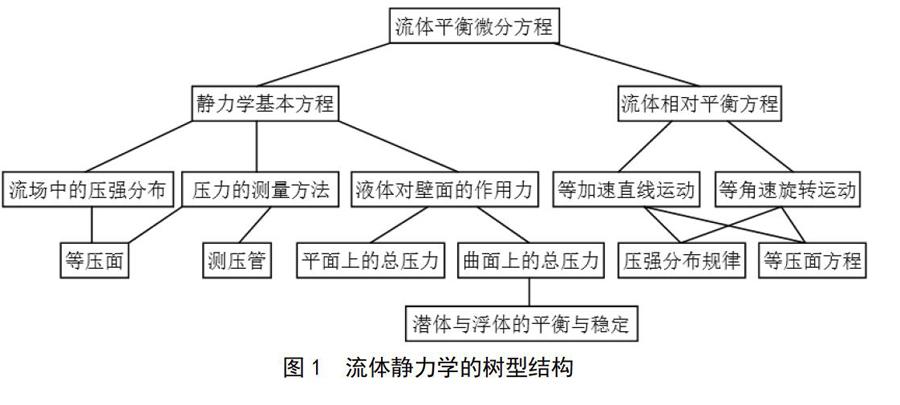
流体力学是研究流体在各种力作用下的平衡和运动规律的科学。因此，流体平衡微分方程（公式1）、理想流体运动微分方程（公式2）和实际流体运动微分方程（公式3）就是流体力学教学中树型结构的主干部分。这三个方程的实质就是牛顿第二定律在流体力学中的应用。流体力学的其他教学内容都是围绕这三个方程展开，或是这三个方程的延伸和应用。

f-▽p/ρ=0 （1）

f-▽p/ρ=du/dt=?u/?t+（u?▽）u （2）

f-▽p/ρ+ν▽2u=du/dt=?u/?t+（u?▽）u （3）

下面以流体静力学为例来加以说明。流体的静力学就是以流体平衡微分方程为基体的小型树状结构，如图1所示。由图1可以看出，流体平衡微分方程就是流体静力学问题的分支主干，并延伸出重力场下的平衡方程和相对平衡方程两个分支，由此可继续向下不断延伸。流体力学中的其他章节也都是一个这样类似结构的小型树，教师可以依据授课学时，在保证主体内容完整的情况下，对分支知识点进行取舍。

3 构建多层次理论知识体系

为了教会学生运用联系和发展的观点学习流体力学理论，提高学生综合运用知识的能力，在课堂教学时对每一个重要的流体力学概念和方程都会由浅入深，采用不同方法、不同视角进行解释或推导，以便开阔学生思路，加深学生对重要流体力学概念和方程中各项所代表的物理含义的理解。这种教学方式一方面可以让学生扎实地掌握流体力学中的相关概念和方程，也能够帮助学生构建多层次理论知识体系。下面以连续性方程为例，加以具体说明。

为了让学生更加深刻地理解连续性方程的实质就是质量守恒定律在流体力学中应用，授课时分三个层次对连续性方程进行推导。

首先，选择一段流管作为控制体，推导总流的连续性方程。由流管的定义可知，流体不能穿过流管侧壁，因此，流体只能通过流管两端的过流断面进出控制体。如图2所示，假设流体从A1断面流入，A2 断面流出，依据质量守恒定律，在单位时间内通过A1流入控制体的流体质量减去通过A2流出控制体的流体质量应等于单位时间流管内流体质量的增加量，如方程（4）所示：

∫∫A1ρudA- ∫∫A2ρudA=∫∫∫v?ρ/?tdv （4）

若流动定常，则方程（4）右边项为零。若流体不可压缩，且用平均速度替代流体质点的速度，方程（4）就可转换为一维流体连续性方程。

通过分析推导，学生已经对流管内的连续性方程有了初步的理解和认识。接下来，选择微元六面体（图3）作为控制体，推导三维流动的连续性微分方程。由于有了流管连续性方程的推导经验，学生很自然地明白，通过时间段dt，流入微元六面体的流体质量减去流出微元体的流体质量应等于微元内流体质量的增加量，列出等式并化简化，就得到连续性微分方程（5）：

?ρ/?t+▽·（ρu）=0 （5）

如果流动是定常的，则方程（5）的第一项为零。若流动不可压，方程（5）简化为速度的散度▽?u为零。从物理角度看，由于密度为常数，微元六面体内的流体质量不发生变化，因此流入微元体的流体质量应等于流出微元体的流体质量。从数学角度看，速度的散度表示流体的相对体积膨胀率，不可压缩流体体积膨胀率为零。

最后，借助系统的质量守恒定律和雷诺输运定理推导积分形式的连续性方程（6）：

?∫∫∫vρdv/?t+∫∫Sρu·ndS=0 （6）

可以看出，方程（4）和方程（6）形式上十分相似，不同之处在于方程（6）的控制体为任意形状，而方程（4）的控制体为流管。换句话说，方程（4）是方程（6）的一个特例，方程（6）则是方程（4）的一个延伸。若对方程（6）采用高斯公式，还可以推导出连续方程的微分形式（5）。

通过三种不同的方法推导连续性方程，让学生对质量守恒定律有了更深刻的理解，也对连续性方程中的物理意义更加明确，同时学会将高等数学和流体力学联系在一起，不再单纯孤立地学习某一学科，拓宽了思路和视野。

4 结语

本文从激发学生的创新意识、培养创新能力出发，对流体力学教材重新整合，建立树型结构教学内容体系，即在透彻理解教材内容，明确各章节逻辑关系的基础上，将授课内容划分成树型结构，方便教师把握教学的主干和分支点，合理安排教学内容。同时提出多层次理论知识教学模式，对流体力学的重要方程和概念由浅入深，采用不同的方法、不同的视角进行推导或解释，教会学生运用联系和发展的观点学习流体力学理论，提高学生综合运用知识的能力。这种加强基础、注重素质的教学模式，充分体现了“培养能力、激励创新”的先进教学理念，提高了流体力学的教学质量，改善了教学效果。

参考文献

[1]徐冬英.模块式教学改革研究：以《工程流体力学》为例[J].绍兴文理学院学报，2013，33（11）：13-16.

[2]王发辉，桑俊勇，张丹.“流体力学”立体化教学体系的构建[J].中国电力教育，2009（12）：102-103.

[3]张明辉，陈庆光.“流体力学”多元化课堂教学模式的构建[J].中国电力教育，2013（1）：64-65.

[4]梁延鹏，曾鸿鹄，李艳红.基于实践能力培养的流体力学实验教学改革[J].当代教育理论与实践，2012，4（11）：155-157.