例题教学应从“解题”走向“思想”
2016-05-14张海强孟盛
张海强 孟盛
【摘 要】微积分是继欧几里得几何之后,数学发展史中的一个创造,极限思想则是微积分的基础。从历史发展来看,极限思想的建立是一个渐进的过程,因此新课程教科书为帮助学生建立极限思想作了诸多尝试。从高考对极限思想的考查来看,结果不尽如人意,因此宜加强习题教学的研究,使习题教学从数学知识的教学走向数学思想(方法)的教学,甚至数学观念的教学。
【关键词】极限思想;渐近线;下确界;数学阅读;习题教学
【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009(2016)28-0039-03
【作者简介】1.张海强,江苏省宜兴中学(江苏无锡,214200)教师,高级教师,江苏省特级教师;2.孟盛,江苏省宜兴中学(江苏无锡,214200)教师。
极限思想是一种重要的思想方法,是微积分的基础,是连接初等数学与高等数学的桥梁。随着高中对导数内容学习的深入,极限思想不可避免地从幕后走向台前,以“正统”的姿态进入了高中教材,极限思想已然成为高中数学思想方法的重要内容。但从2010年和2013年江苏高考对极限思想的考查来看结果不尽如人意,学生尚缺乏运用极限思想解决问题的意识和能力,极限思想并没有在学生的头脑中“扎根”。本文以2010年和2013年江苏省数学高考试题中的压轴题为例,呈现考生的不严密解答,并做出相关分析,基于此给出对极限思想教学的一点思考。
一、试题与不严密解答
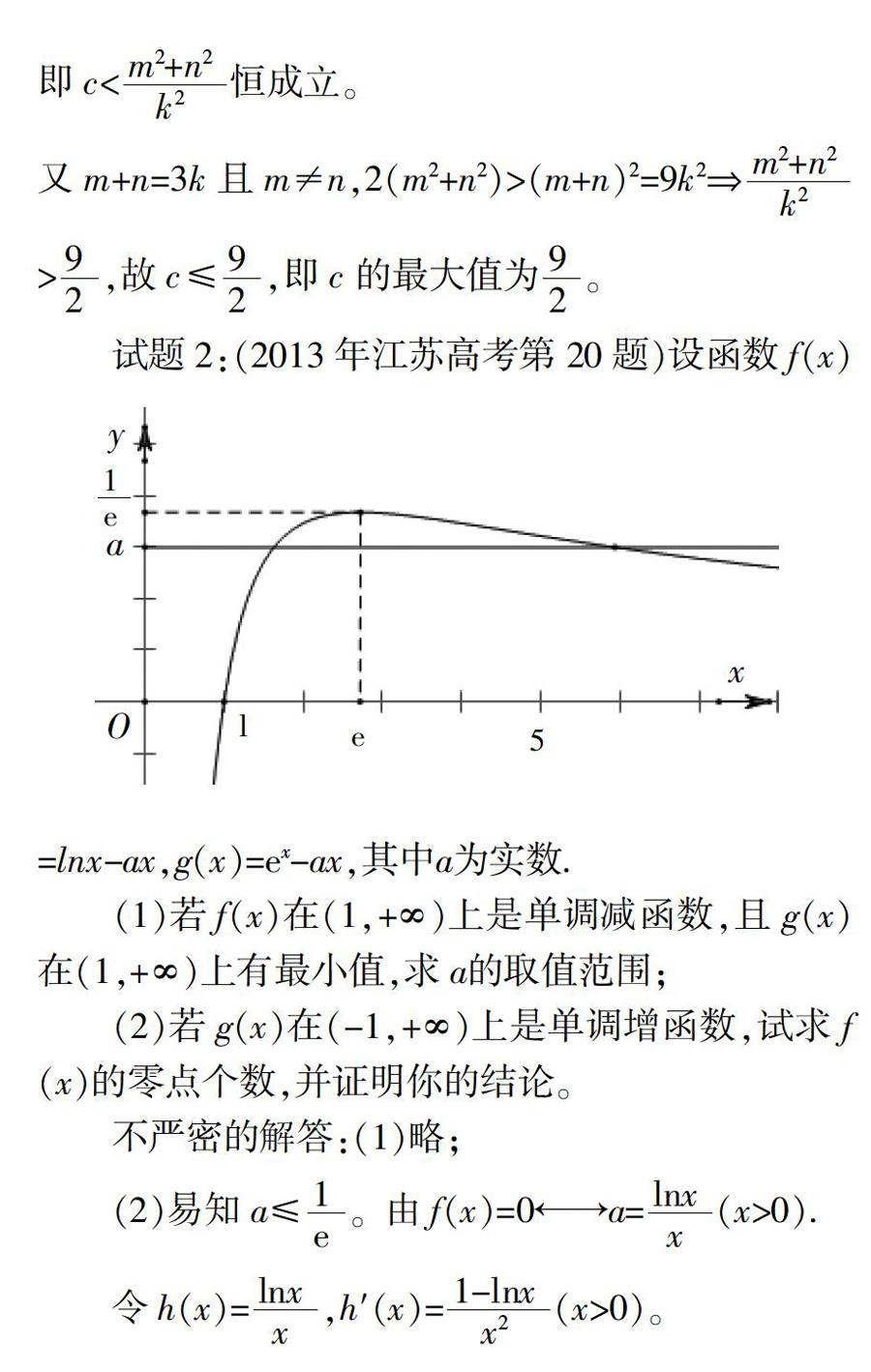


四、两点思考
首先,极限思想的建立是一个渐进的过程。就历史发展的角度而言,极限思想的萌芽可以追溯到古代。在古希腊、中国和印度数学家的著作中,已不乏朴素的极限思想。如《庄子·天下篇》中的名言“一尺之棰,日取其半,万世不竭”,刘徽的割圆术和古希腊的穷竭法等。17世纪英国物理学家牛顿与德国数学家莱布尼兹以无穷小概念为基础创立了微积分,极限思想得到了进一步的发展。到18世纪极限思想得到初步的完善,法国数学家达朗贝尔等人先后对极限作出了各自的定义。19世纪法国数学家柯西比较完整地阐述了极限概念及其理论。由认知的历史发生原理可知,学生头脑中极限思想的建立应符合极限思想的历史发展过程。
教科书在内容的编排上也充分考虑了这一渐进过程,以苏教版高中教材为例,必修一“阅读”栏目中“ 的含义”、必修二“问题与建模”栏目中“体积的近似计算”、“阅读”栏目中的“祖暅原理”以及选修2-1正文中“双曲线的渐近线的证明”等内容均为学生极限思想的建立提供了良好的素材和合理的时机。
因此,笔者以为应切实加强数学阅读教学,而且首先从阅读教科书开始,苏教版高中教材中设置了“阅读”“链接”“思考”“数学探究”等栏目,这些栏目的内容或有利于学生构建完整的知识的结构,或有利于扩展学生的数学视野、丰富学生的“智力背景”,或有利于参悟某种数学观念。
其次,应当改进习题教学,立足于优化学生思维。苏霍姆林斯基说:学生在课堂上的脑力劳动修养乃是教师劳动修养的一面镜子。以此类推,学生在答卷上的脑力劳动修养何尝不是教师劳动修养的一面镜子?
试题1和试题2的不严密解答大多选择“分离参数法”,这正是平时教学和练习中滥用“分离参数法”形成的思维定势。因此,习题教学应着力提升学生分析问题的能力,注重通性通法,淡化技巧。
试题1和试题2的不严密解答说明学生对极限思想浑然不知,究其原因是教师在平时教学中缺乏高观点的指导,缺乏极限思想的渗透,因此,习题教学应从数学知识的教学走向数学思想(方法)的教学,甚至数学观念的教学。
试题1和试题2的不严密解答表现出了“千人一面”的现状,究其原因是教师满堂灌的结果,扼杀了学生的主动性和创造性,学生学会的仅仅是“依样画葫芦”,臣服于教师的权威,缺乏质疑的品质。因此,习题教学需要留白,以提供学生“悟”的时间和空间,彰显个人的特色与风采。
【参考文献】
[1]华志远.透视高考热点,漫话极限思想[J].高中数学教与学,2014(17).
[2]张海强,史豪峰.图像固直观,推理更精采[J].中学数学:高中版,2014(01).
