“学”即研究
2016-05-14曾荣
【摘 要】研究性学习提倡用类似科学研究的方式探究并获取和应用知识,它有利于学生学习和感受数学知识中凝聚的数学智慧,形成初步的数学学科素养。数学教学可以将研究性学习融入问题情境的创设之中、数学模型的建构之中、研究方法的探求之中、数学本质的揭示之中以及数学应用的过程之中,以帮助学生强化数学抽象的意识,提高数学建模的能力,形成科学探究的自觉,培养严谨推理的习惯和提升问题解决的能力。
【关键词】高中数学;研究性学习;学科素养
【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009(2016)28-0016-03
【作者简介】曾荣,江苏省南通市教育科学研究中心(江苏南通,226000)教研员,江苏省特级教师,正高级教师。
数学教学的价值追求不仅是数学知识与方法的传授,更重要的是数学素养的培养。数学素养是指数学学科的“四基”“四能”与“基本思维形式和思维方法”。“四基”指基础知识、基本技能、基本思想和基本活动经验;“四能”指发现问题、提出问题、分析问题、解决问题的能力;“基本思维形式和思维方法”指演绎和归纳的“双向思维”[1]。数学核心素养通常包含数学抽象、数学建模、逻辑推理、直观想象、数学运算、数据分析等几个方面。数学研究性学习提倡用类似科学研究的方式探究并获取和应用知识,它有利于学生在掌握数学知识的同时,学习和感受数学知识中凝聚的数学智慧,形成初步的数学学科素养。
本文以2015年12月举行的江苏省高中数学青年教师优秀课观摩与评比活动中一些课例的精彩片段为例,说明将研究性学习活动融入数学课堂教学之中以引领学生数学学科素养形成的具体策略。
一、研究性学习融入问题情境的创设之中,强化数学抽象的意识
现代数学的发展表明,数学的研究源于对现实世界的抽象,通过基于抽象结构的符号运算、形式推理、一般结论等,理解和表达现实世界中事物的本质、关系与规律。数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程。数学抽象是数学的基本思想,数学抽象的素养是形成理性思维的重要基础,它贯穿在数学的产生、发展、应用的过程中。在数学教学活动中,教师将研究性学习渗透于问题情境的创设之中,将有利于数学抽象意识的强化。
【案例1】“导数在研究函数中的应用——单调性”的问题情境创设(江苏省南通中学秦霞执教)
“导数在研究函数中的应用——单调性”的教学难点是引导学生发现导数与函数单调性之间的联系,而这两个概念都是非常抽象的,学生很难直接感知。秦霞老师在问题情境创设阶段,利用“生活中汽车灯光的指向与上下坡之间的联系”这一常见问题,有效地完成了两次抽象。
第一次抽象:引导学生发现道路可以抽象成函数的图象,灯光可以抽象为切线,这样问题就转化为切线斜率正负与曲线上升下降的联系。
第二次抽象:适当建系后,将曲线看做是函数y=f(x)上的一段图象,那么切线斜率即为函数在该点处的导数,顺势猜想结论,感知导数正负与函数单调性之间的联系,从而轻松高效地引入课题,成功激发了学生的求知欲,也体现了“生活中处处有数学”的教学理念。抽象过程如下图1所示。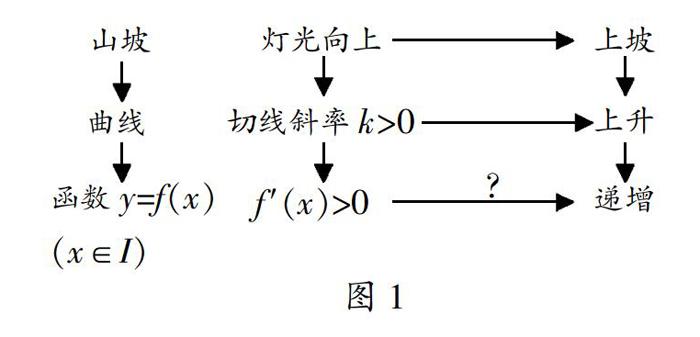
二、研究性学习融入数学模型的建构之中,提高数学建模的能力
数学模型构建了数学与外部世界的桥梁,是数学应用的基本形式。数学建模是应用数学解决实际问题的基本手段,是推动数学发展的外部驱动力。数学建模突出了学生系统地运用数学知识解决实际问题的过程,帮助学生逐步积累数学活动经验,培养学生应用能力和创新意识。在数学教学活动中,加强数学建模核心素养的培养,有利于学生养成用数学的眼光观察现实世界的习惯,有利于学生发展用数学的思维分析实际问题的能力,有利于学生形成用数学的语言表达实际问题的能力。数学模型的建构过程,就是一种研究性学习的过程。
【案例2】“函数y=Asin(ωx+φ)的图象”的数学建模过程(南京师范大学附属中学丁菁执教)
苏教版教材在编写“函数y=Asin(ωx+φ)的图象”这部分内容时,通过物理中的“简谐运动”进行过渡。而“简谐运动”在高一物理学习中尚未涉及,故这一情境无疑成了一种空中楼阁。丁菁老师在教授这部分内容时,没有采用这种虚拟模型,而是将建模过程设计成如下两个环环相扣的研究性学习过程。
环节1:如图2,摩天轮的半径为Am(A>0),摩天轮逆时针做匀速转动,角速度为ωrad/min(ω>0),如果当摩天轮上点P从图2中点P0(P0在x轴正半轴上)处开始计算时间。请在图2所示的坐标系中,确定时刻xmin时点P的纵坐标y。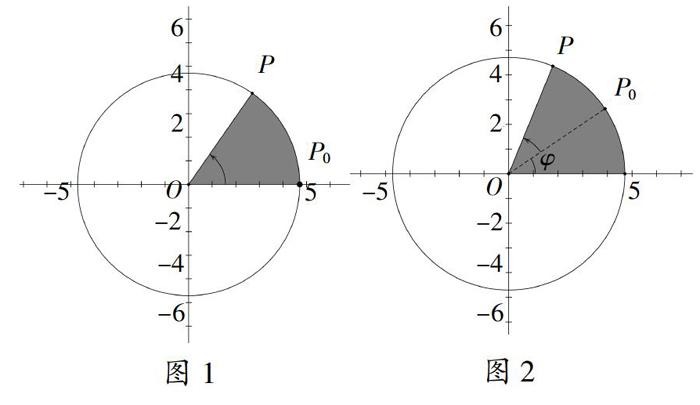
环节2:在上述问题中,如果当摩天轮上点P从图3中点Po处开始计算时间。请在图3所示的坐标系中,确定时刻xmin时点P的纵坐标y。
以上处理策略让学生真实地经历了数学建模的过程,感受到构建数学模型的必要性。同时,也让学生领悟到函数y=Asin(ωx+φ)与y=Asinωx的内在联系,如若将问题进一步特殊化,让A=ω=1,则将数学模型转化为y=sinx。这种由未知到已知,由一般到特殊的转化的策略正是后续学习的基础。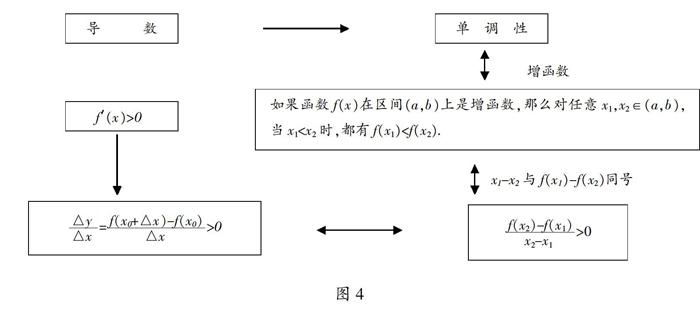
三、研究性学习融入研究方法的探求之中,形成科学探究的自觉
“研究性学习是指学生在教师指导下,以类似科学研究的方式去获取知识和应用知识的学习方式”[2]。研究性学习区别于接受式学习的一个重要标志是具有较明晰的学习计划,具有为完成这一计划而拟定的研究方法,当然,这种计划与方法需要在执行的过程中根据实际情况而调整。为了形成科学有效的研究方案,教师要善于运用“头脑风暴”,集思广益,让学生对问题进行全面系统的分析,或将问题进行分解,使其更具体、更清晰,进而抓住主要矛盾,找到解决问题的关键点,确定问题的研究方向。长期这样注重方法形成的教学,有利于学生形成科学探究的自觉,达到“授人以鱼不如授人以渔”的目的。
【案例3】“函数y=Asin(ωx+φ)的图象”的研究方法探求实录(江苏省南通中学张勤执教)
张勤老师在研究目标确定以后,顺势提出了这样的问题:如何在函数y=sinx图象的基础上研究函数y=Asin(ωx+φ)的图象?请结合以往经验给出研究方案。这种先行组织者策略,为学生自主探究提供了广阔的空间。学生自主提出了特殊到一般的策略,提出了“五点作图”的方案,提出了通过图象的变化规律来研究的方案,提出了“分而治之,各个击破”的设想。教师并未止于学生的设想,而是进一步追问学生产生这些想法的学习基础,与以往的研究二次函数、指数函数和对数函数的方法进行比较,强化学生科学探究的意识,这无疑对学生良好数学素养的养成是极为有利的。
四、研究性学习融入数学本质的揭示之中,培养严谨推理的习惯
著名数学教育家弗赖登塔尔指出:从教学认识过程的任务来看,其根本目的不在于仅仅获得和验证真知,更主要的是为了在一定知识经验之上构建学生主体的新的认知活动结构和实践行为能力,学生主体在认知过程中的建构活动本身即是一种创造的过程。通过研究性学习完成知识的建构、本质的揭示的过程,需要通过严谨的逻辑推理去完成。
【案例4】“导数在研究函数中的应用——单调性”的数学建构过程(江苏省南通中学秦霞执教)
在探究导数与函数单调性之间的联系时,如何使研究的问题既具体直观又严谨规范,这是本节课教学的一个难点。秦霞老师在问题情境直观感知、抽象猜想的基础上,根据学生的认知规律让学生自主举例,独立验证,感悟猜想的合理性。思维活动并未止于这种直观感悟,此时教师又从“数”的角度,借助图4所示的逻辑链,进一步引导学生抓住导数和单调性的定义之间的联系来提炼一般性的结论。整个研究过程从感知,到验证,再到说理,既直观又严谨,体现了数学研究性学习的方法性和严谨性。理性分析过程如图4。
五、研究性学习融入数学应用的过程之中,提升问题解决的能力
“研究性学习是学生在教师指导下,从自然现象、社会现象和自然生活中选择和确定研究专题,并在研究过程中主动地获取知识、应用知识、解决问题的学习活动”[3]。培养学生发现问题、提出问题,从而解决问题的能力是研究性学习的基本目标;在应用知识解决数学问题的过程中,进一步巩固数学知识、感悟数学方法、全方位提升数学素养,则是研究性学习的基本任务。
【案例5】“导数在研究函数中的应用——单调性”的数学应用过程(江苏省盐城中学杨志明执教)
杨志明老师在得出导数与函数单调性的关系之后,并没有停留在简单套用结论解决基本问题的层面,而是立足简单三次函数的单调性,将数学应用过程变成了一个研究性学习过程,通过不断追问的方式步步深入,从数和形两个角度深入研究导函数与原函数之间的关系。具体过程如下:
例题:确定函数f(x)=2x3-6x2+7在哪些区间上是增函数。(师生合作解决本题,巩固导数法求函数的单调性)
追问1:根据刚才研究的单调性,你能否作出函数f(x)=2x3-6x2+7的示意图?(教师在学生作图的基础上,通过计算机作图验证)
追问2:刚才我们通过导数求出了函数的单调区间,进一步画出了函数的示意图。反之,如果我们知道了函数的图象,能否直接画出导函数的示意图呢?
追问3:通过以上研究,我们知道了如果在某区间上f′(x)>0,那么f(x)为该区间上的增函数。反之,如果f(x)在某区间上单调递增,那么在该区间上每一点都有f′(x)>0成立吗?(学生遇到一定困难,教师提示结合函数f(x)=x3进行判断)
追问4:我们本节课解决的f(x)=ex-x和三次函数的单调性,都可以看成是基本的初等函数进行四则运算得到的,下面请同学们参照这样的方法自己构造函数,并尝试用导数判断出单调性。
综上所述,将研究性学习融入数学课堂教学,让学生亲历知识产生与形成的研究过程,使知识发现、方法习得与素养形成有机结合与高度统一,是数学教育永恒的追求。
【参考文献】
[1]岳辉,和学新.学科素养研究的进展、问题及展望[J].教育科学研究,2016(01).
[2]张肇丰.试论研究性学习[J].课程·教材·教法,2000(06).
[3]钟启泉,等.为了中华民族复兴为了每位学生的发展[M].上海:华东师范大学出版社,2001.
