例谈数学思想和方法在解题中的渗透オ

陈锦钢

所谓数学思想就是指对数学本质和规律的认识，也是我们解决数学问题的核心手段数学思想是解题的灵魂，数学方法则是解题的利器，这两种相互渗透、相互联系，密不可分数学方法在量的积累后，会产生质的变化，即是数学思想的形成通过数学思想方法的教学，可以在数学知识与解题中架设桥梁，对学生知识积累、能力提升和综合素养产生影响本文将从实际问题出发，探究如何实现数学思想方法在教学中的渗透

一、在解题中渗透化归思想

化归思想是指在解决数学问题时，联系新旧知识，将欲解决的陌生问题向学生们所熟悉的方面进行转化，借助几何图形、数学公式，实现化繁为简、化难为易化归思想在解决几何图形问题、代数证明题、分式转化题中都有着显著的优势在化归思想的使用中，常常会涉及待定系数法、配方法、转化法等通过此类数学思想的教学，可以帮助学生掌握多种数学方法，对提高学生解题效率帮助明显

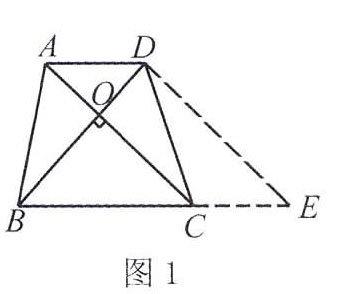
例1如图1所示，在梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD相交于点O，且AC⊥BD，AD=3，BC=5，试求AC的长

解析首先，从题中所给条件来看，要想直接求出AC的长度似乎是不可能的对此，我们必须利用化归思想进行转化，将我们未知的边长向已知边长进行转化要想将AC边与已知边联系起来，我们绘制出了如图虚线所示的辅助图形绘制过程如下：过D点作DE⊥BD，并交BC的延长线于点E，得到AD=CE、AC=DE然后，由题中已知条件AC⊥BD，则可知BD⊥DE再由AB=CD，我们可以得到AC=BD，再结合AC=DE，最终得到BD=DE在直角三角形BDE中，BE2=BD2+DE2，可以求得BD=[KF（]2[KF）]2BE=4[KF（]2[KF）]最后利用BD=AC，我们可以求出AC的长度为在本题中，我们利用梯形对角线互相垂直的特点，通过将对角线进行平移，将等腰梯形转化成平行四边形和直角三角形如此一来，我们在化归思想的指导下，利用几何图形的转化实现了本题的求解

二、在解题中渗透数形结合思想

在中学数学教学中，数形结合思想是联系代数与几何的桥梁，代数即是数，几何即是形从表面上来看，这两者似乎是分隔的，但在数形结合思想的帮助下，数量关系和几何图形可以进行相互转化通过数形结合思想的教学，学生们得以将抽象的图形问题代数化，也能将复杂的代数问题图形化在数学解题中，数形结合思想可以拓宽学生思维，有利于提高学生分析问题和解决问题的能力

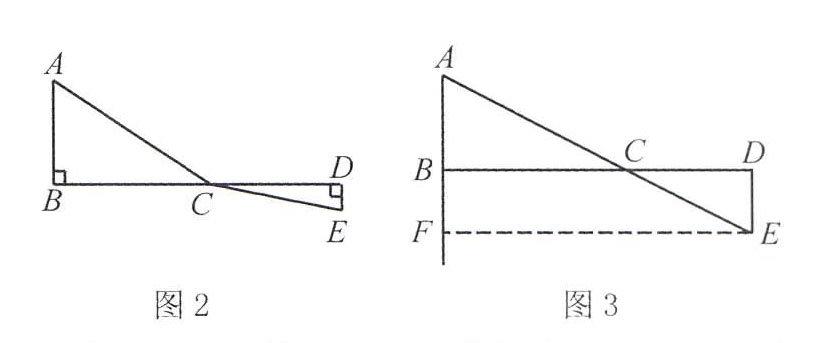
例2如图2所示，C为线段BD上的一动点，分别过点B、D作AB⊥BD、ED⊥BD，连接AC、EC已知AB=5，DE=1，BD=8，设CD=x

（1）试用含x的代数式表示AC+CE的长；

（2）试问点C满足什么条件时，AC+CE的值最小；

（3）根据（2）中的规律和结论，请构图求出代数式的最小值

解析对于第一问，我们直接利用勾股定理便可以求得，即是将几何图形转化成代数表达，可得对于第二问，要使AC+CE的值最小，也就相当于要求出第一问中的代数表达式的最小值此时，很多学生会直接利用第一问中得到的代数表达式进行求解但中学生受到自身知识的局限性，他们往往难以直接求出此时，我们不妨引导学生利用数形结合的知识进行求解对此，教师要求学生对该几何图形进行观察，要求他们对AC+CE的长度表达进行探究观察后，我们不难发现本题的考点就是求两点之间的最短距离，结合“两点之间直线距离最短”的定理，我们很容易得到当C点位于BD和AE交点处时，AC+CE即可取得最小值对于第三问，我们不妨在第二问的猜想上绘制辅助线，如图3所示那么，代数式的值即相当于线段AE的长度于是，在直角三角形AEF中，AF=AB+DE=6、EF=BD=8，利用勾股定理可得AE=10在本题中，我们利用数形结合思想，通过对代数问题与几何知识之间的反复转化，实现了对本题求解过程的简化，最终顺利求解出正确答案

三、在解题中渗透建模思想

数学建模是解决实际问题的有效手段，通过数学模型的建立，我们可以帮助学生将课堂知识与实际问题相联系，实现中学数学知识的应用化和实践化数学建模思想是指从问题的关系量分析入手，通过抽象和假设的方法，对实际问题建立对应的解题模型通过数学建模思想的教学，我们可以拉近课堂与学生生活的距离，帮助学生认识到数学知识的重要性，从而激发学生的数学学习兴趣

例3某水果批发市商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱

（1）求平均每天销售量y箱与销售单价x元之间的关系；

（2）求该销售商平均每天的销售利润W元与销售价x元之间的关系；

（3）当每箱苹果售价多少元时，可以获得最大利润，最大利润是多少？

解析本题属于实际数学应用题，对学生的审题能力和函数知识提出了较高的要求，对学生的数学建模能力进行考查首先，对于第一问，我们从题中已知信息可得每天销售量与单价之间的关系，即是y=90-3（x-50）=-3x+240第二问同样如此，只是较第一问相对复杂一点而已，基本思路还是一样的每天利润W=（x-40）（-3x+240）=-3x2+360x-9600此时，要求每日销售利润的最大值就是相当于求解该二次函数模型的最值利用二次函数知识，我们可以迅速地求出当售价为55元时，平均每日销售利润可以达到最大值1125元在新课改背景下，中考数学对学生们实际问题的应用考查越发的注重数学建模思想作为解决实际问题的重要途径，我们必须在日常的教学中进一步加以强化和重视

总之，数学思想方法是中学数学教学的核心在平时的数学教学中，我们不仅需要把握好以上的几类数学思想教学，更要不断探究，为学生们创设出更多有效的数学思想方法教学模式