Conformal Killing Vectors in LRS Bianchi Type V Spacetimes

Suhail Khan,Tahir Hussain,,∗Ashfaque H.Bokhari,and Gulzar Ali Khan

1Department of Mathematics,University of Peshawar,Khyber Pakhtoonkhwa,Pakistan

2Department of Mathematics and Statistics,King Fahd University of Petroleum and Minerals,Dhahran 31261,Saudi Arabia

1 Introduction

The Einstein’s Field Equations(EFEs)are the core of mathematical formulation of general theory of relativity.These field equations constitute a set of ten coupled non-linear partial differential equations in ten independent components of the metric tensor.Due to this highly nonlinear nature of EFEs,only a limited number of their exact solutions are known.[1−2]As for as spacetime symmetries are concerned,they assist in both generation of new exact solutions as well as classification of known exact solutions of the EFEs.

Among the well-known spacetime symmetries,conformal symmetries are of particular interest.Mathematically,given a manifold M,the conformal symmetry is given by a vector ξ,such that when the metric moves along the integral curves generated by ξ,its Lie derivative satisfies the relation:[3]

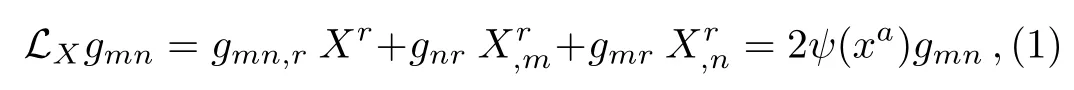
where LXsignifies Lie derivative operator along the vector field ξ and ψ :M → R is some smooth real valued function,called conformal factor.When ψ=0,the solutions of Eq.(1)are referred as Killing vectors(KVs).Additionally,if ψ,a=0,then the CKVs are called homothetic vectors(HVs).A CKV for which the conformal factor is not constant is known as proper CKV.It is called special conformal Killing vector if ψa;b=0.In flat Minkowski and vacuum spacetimes,every CKV is special conformal.[3]The collection C(M)of all CKVs on a spacetime M constitutes a finite dimensional Lie algebra under the Lie bracket operation,called conformal algebra,such that dimC(M)≤15.For a conformally flat spacetime M,we have dimC(M)=15.Conversely if dimC(M)=15 and in fact when dimC(M)>7,then M is conformally flat.[3]

The notion of inheriting conformal Killing vectors(ICKVs)in fluid spacetimes was introduced by Coley and Tupper.[4]A CKV ξ is said to be inherited by the physical fluid source represented by the energy-momentum tensor if the fluid flow lines are mapped conformally into the fluid flow lines,that is:[4]

where uais the four velocity of the fluid.

In literature,conformal symmetries have been studied by different authors.Maartens and Maharaj[5]investigated conformal symmetries in Robertson–Walker and pp wave spacetimes,showing that non- flat conformally flat pp waves always admit G6of motions and G1of proper homothetic motions,but do not admit in general special conformal motions.Moopanar and Maharaj[6]explored conformal symmetries in shear-free spacetimes with spherical symmetry by solving the conformal Killing equation,subject to some integrability conditions.The authors showed that time-like and inheriting conformal Killing vectors are admitted by these spacetimes.Hall et al.[7]showed that if a null Einstein–Maxwell spacetime admits a proper CKV,it must be either a pp wave or a generalized Goldberg–Kerr metric.Amenedo et al.,[8]studied exact perfect fluid solutions of EFEs admitting a Lie algebra of CKVs and considering a specific class of perfect fluid models admitting three CKVs acting on a two-dimensional surface,they obtained a particular exact perfect fluid solution.Saifullah et al.[9]investigated conformal motions in plane symmetric static spacetimes.The authors found the general solution of conformal Killing equations and presented the general form of the CKV for these spacetimes.Chudecki and Dobrski[10]studied proper conformal symmetries in self-dual Einstein spaces.They showed that the existence of proper CKV in these spacetimes implies the existence of isometric,covariantly constant and null Killing vector.Hall and Steele[11]made a general discussion on conformal symmetries and,as a conclusion;they gave a remarkable statement about the maximum dimension of conformal algebra of non conformally flat spacetimes.Coley and Tupper[12]studied perfect fluid spherically symmetric spacetimes,which admit a proper ICKV.The authors found that,other than FRW spacetimes,static Schwarzschild interior,conformal FRW and generalized Gutman-Be’spalko-Wesson are the only perfect fluid spherically symmetric spacetimes in which the proper CKVs are inheriting. Moreover,all these spacetimes are either conformally flat or they admit a CKV which is either parallel or orthogonal to the fluid 4-velocity.The same authors considered spherically symmetric spacetimes representing an anisotropic fluid,which admit a proper ICKV.All such spacetimes are found and it is shown that,except the case when they become conformally flat,the ICKVs lie in the(t,r)plane.[13]

Bianchi type V cosmological models are natural generalization of FRW models with negative curvature.These models are of interest because they include isotropic special cases and allow arbitrary small anisotropy at some instant of cosmic time.This property makes these models suitable candidates for the Universe.Further,Bianchi type I,V,and IX models include the homogeneous and isotropic FRW models as their particular cases according to t=constant,zero,negative or positive.Although homogeneous but anisotropic models are more restricted than the inhomogeneous models,they describe a number of observed phenomena quite satisfactorily.[14]

In this note,we study CKVs and ICKVs in LRS Bianchi type V spacetimes.It is worth noting that if we choose A=B and q=0,the Bianchi V spacetimes reduce to the standard Friedman models,which admit a conformal time-like Killing vector.In k=0 case,the Friedman spacetime metric becomes conformally flat and admits a maximal set of 15 CKVs,which are same the CKVS of the flat Minkowski spacetime metric.[15]The paper is organized as follows:In Sec.2,we present conformal Killing’s equations and their general solution,subject to some integrability conditions.Also,assuming separability of functions appearing in the components of CKVs,the conformal vectors are determined explicitly.Section 3 is devoted to investigate ICKVs in LRS Bianchi type V spacetimes.A brief summary and discussion of the work is given in the last section.

2 Conformal Killing’s Equations and Their Solution

We consider the metric representing locally rotationally symmetric(LRS)Bianchi type V spacetimes in Cartesian coordinates,[1]

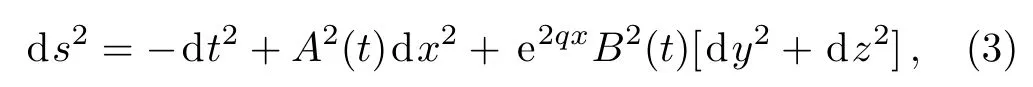
where A and B are nowhere zero functions of t only with q∈R.It reduces to Bianchi type I spacetimes metric if q=0.The above metric admits the following four linearly independent spatial KVs:[1]

Using Eq.(3),the conformal Killing’s Eq.(1)gives rise to the following system of ten coupled partial differential equations:

where a prime on a metric function represents its derivative with respect to t.We find CKVs by solving the above system.differentiating Eqs.(7)and(10)with respect to z,Eqs.(8)and(11)with respect to y and Eq.(13)with respect to t and x respectively,give rise to the following identities:

Solving Eq.(15)and using the obtained results in Eq.(5),we get the following system:

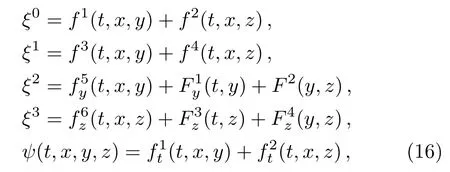
where fiand Fj,for i=1,...,6 and j=1,...,4 are unknown functions which arise during the integration process.To obtain the explicit form of the component of CKV,we exploit the system given by Eqs.(5)–(14).Using Eq.(16)in Eqs.(7),(8),(10),(11),and(13)gives,

where we have used

and Fkdenote functions of integration for k=5,6,7.Subtracting Eq.(12)from Eq.(14),we get

differentiating Eq.(18)with respect to t,x and y respectively and performing some basic algebraic manipulation,one can re-write the system given by Eq.(17)in the following form:

Now differentiating Eq.(12)with respect to z,Eq.(14)with respect to y and z and using these results in Eq.(18),determines CKVs and the conformal factor(up to some functions of t and x):

where c1,c2,c3∈ R.The above system constitutes a general solution of the conformal Killing’s Eqs.(5)–(14),subject to the following integrability conditions:

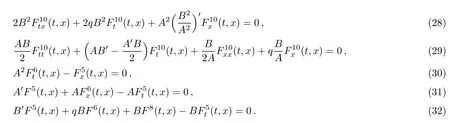
To write the CKVs,conformal factor and the integrability conditions in a more compact form,we introduce new variables

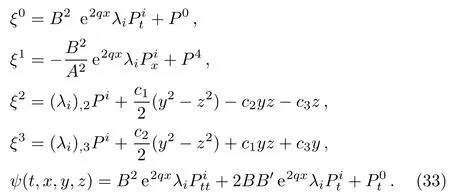
and denote P0=F5,P4=F6.In these variables,it is straightforward to write CKVs and the conformal factor appearing in Eq.(20)as follows:

Accordingly, the integrability conditions, given by Eqs.(21–(32),can be re-written in a more compact from as:

where ki=0,−c2,c1,for i=1,2,3 respectively.To obtain the explicit form of CKVs,one needs to solve the above conditions.It can be noticed that the above conditions are highly non-linear and cannot be solved directly as they stand.We solve these conditions,Eqs.(34)–(39),by assuming that the unknown functions Pk(t,x)are separable as sum of two functions in their arguments,i.e.Pk(t,x)=Gk(t)+Hk(x)for k=1,2,3,4 respectively.In the light of this assumption,one can easily solve the system of Eqs.(34)–(39)to obtain:

subject to the following condition:

which can be easily solved to obtain:

where α is a non-zero constant.From Eq.(40),it is clear that the LRS Bianchi type V spacetimes admit six independent CKVs,provided that the metric functions satisfy the condition given by Eq.(42).In order to obtain the CKVs in some other cases,we consider the following additional cases:

Case 1If we take B(t)=α A(t),then Eq.(42)gives q=0.In this case the metric in Eq.(3)gets the form,

which,in an appropriate frame,is the Friedman flat spacetime metric admitting fifteen independent CKVs.[15]

Case 2If we consider A=A(t)and B=const.=m1,then Eq.(42)can be easily solved to get A(t)=qt+m2.Thus the metric given by Eq.(3),after a suitable rescaling,can be re-written as:

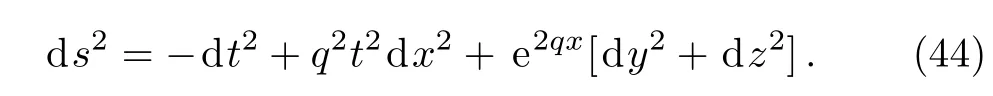
For this metric,the CKVs and conformal factor in Eq.(40)reduce to,

Thus the metric given in Eq.(44)admits six CKVs,one of which is proper CKV given by

Also the dimension of homothetic algebra is fi ve with one proper HV,which can be expressed as

The dimension of group of isometries in this case is four.The non zero commutators of Lie algebra of the above six CKVs is given by

Case 3Here we take A=const.=m1and B=B(t).Eq.(42)gives B=B(t)=m2e−qt/m1,where m26=0.Assuming m1=m2=1,the Bianchi type V spacetimes metric(3)takes the form:

For this metric,the CKVs in Eq.(40)reduce to:

which shows that the metric given in Eq.(45)admit no proper CKV and the CKVs are just HVs in this case with one proper HV,given by

Also the dimension of isometry group is five with four KVs same as mentioned in Eq.(4)and the fifth KV can be expressed as X5= ∂/∂t+∂/∂x.In this case the Lie algebra of the above HVs has the following non zero commutators:

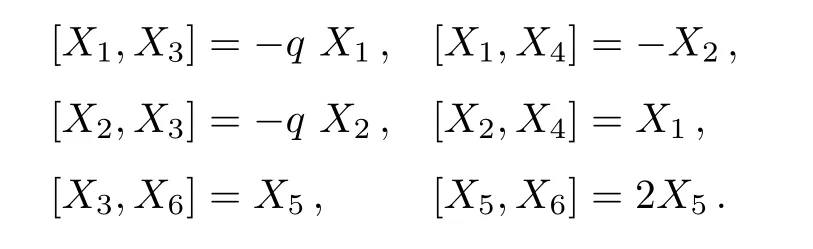
3 Inheriting Conformal Killing Vectors

In this section we investigate the ICKVs by choosing the fluid four velocity vector as ua=δa0.Thus the relation(2)generates the following equations:

which suggests that in Eq.(33)we must have ξ0=P0(t)and Pi=Pi(x),for i=1,2,3.Also Eq.(37)implies P4=P4(x)and the remaining integrability conditions reduce to,

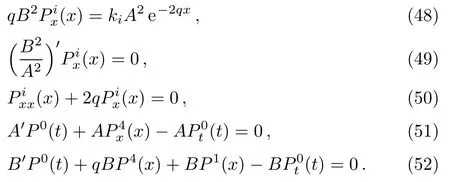
From Eq.(49),two possible cases arise,namely,B 6=α A and B= αA,where α is a non zero constant.In the former case,a complete solution of Eqs.(48)–(52)yield the following ICKVs:

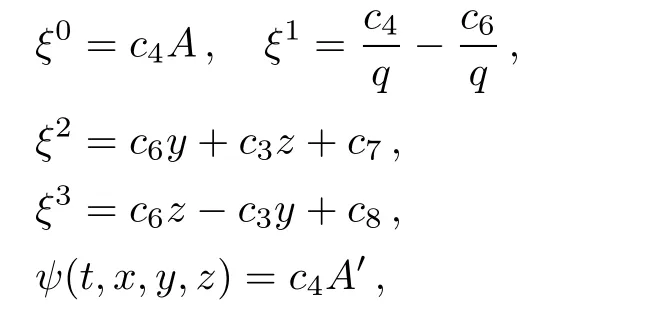
subject to the condition B(A/B)′=1.This result reveals that in this case the LRS Bianchi type V metric admits five independent ICKVs with only one proper ICKV,which is given by X5=A(t)(∂/∂t)+(1/q)(∂/∂x).Also the dimension of homothetic algebra is four with no proper HV and the dimension of isometry group is also four with four KVs same as given in Eq.(4).The Lie algebra of ICKVs has the following non vanishing commutators:

For the latter case,that is when B(t)=αA(t),the metric given in Eq.(3)reduces to,

Solving Eqs.(48)–(52)for the above metric,we obtain the following ICKVs:

which shows that the metric given in Eq.(53)admits seven independent ICKVs,one being proper ICKV given by X7=A(t)(∂/∂t).In this case no proper HV exists and the dimension of isometry group is six with four KVs same as mentioned in Eq.(4)and the remaining two KVs are:

The Lie algebra of these seven ICKVs has the following non-vanishing commutators:

4 Summary and Discussion

In this note,we have given a classification of LRS Bianchi type V spacetimes according to their CKVs.Solving conformal Killing’s equations,we have obtained an explicit form of CKVs along with some integrability conditions.Requiring separation of variables,these integrability conditions are solved completely.It is found that the CKVs satisfy the integrability conditions subject to a differential constraint on the components of the metric.Considering three additional cases,CKVs are obtained.We have also explored Inheriting conformal Killing vectors for LRS Bianchi type V spacetimes and found that these spacetimes admit six independent CKVs and fi ve or seven ICKVs.

Acknowledgments

Authors would like to acknowledge the unknown referees for their useful comments and suggestions.

References

[1]H.Stephani,D.Kramer,M.Maccallum,C.Hoenselaers,and E.Herlt,Exact Solutions of Einstein’s Field Equations,Cambridge University Press,England,Second Edition,Cambridge(2003).

[2]K.L.Duggal and R.Sharma,Symmetries of Spacetimes and Riemannian Manifolds,Kluwer Academic Publishers,Netherland,Amsterdam(1999).

[3]G.S.Hall,Symmetries and Curvature Structure in General Relativity,World Scientific,United Kingdom,London(2004).

[4]A.A.Coley and B.O.J.Tupper,Classical Quant.Grav.7(1990)1961.

[5]R.Maartens and S.D.Maharaj,Classical Quant.Grav.8 503(1991)

[6]S.Moopanar and S.D.Maharaj,J.Eng.Math.82(2013)125.

[7]G.S.Hall and J.Carot,Classical Quant.Grav.11(1994)475.

[8]J.C.Amenedo and A.A.Coley,Classical Quant.Grav.9(1992)2203.

[9]K.Saifullah and S.Yazdan,Int.J.Mod.Phys.D 18(2009)71.

[10]A.Chudecki and M.Dobrski,J.Math.Phys.55(2014)82502.

[11]G.S.Hall and J.D.Steele,J.Math.Phys.32(1991)1847.

[12]A.A.Coley and B.O.J.Tupper,Classical Quant.Grav.7(1990)2195.

[13]A.A.Coley and B.O.J.Tupper,Classical Quant.Grav.11(1994)2553.

[14]R.P.Singh and L.Ladav,Rom.Rep.Phys.63(2011)587.

[15]R.Maartens and S.D.Maharaj,Classical Quant.Grav.3(1986)1005.