Resonances of Spin-1/2 Fermions in Eddington-Inspired Born-Infeld Gravity∗

Qi-Ming Fu(付启明), Li Zhao(赵力), Yun-Zhi Du(杜云芝), and Bao-Min Gu(古宝珉)

Institute of Theoretical Physics,Lanzhou University,Lanzhou 730000,China

1 Introduction

An Eddington-inspired Born-Infeld action(EiBI)for the gravitational field has been put forward by Baados and Ferreira[1]based on the nonlinear electrodynamics of Born and Infeld.[2]This theory can be shown to be completely equivalent to Einstein’s theory of General Relativity(GR)without matter fields,but dramatically deviate from GR in the presence of matter.[1,3]It is shown that the Eddington regime might lead to the avoidance of singularities and modifications to the standard results of stellar astrophysics.EiBI is treated exactly following a Palatini approach,i.e.,the metric and the connection are considered as independent fields.Since EiBI can deviate from GR only with the non-zero energy-momentum tensor,one can expect the significant deviation in the compact objects.In Ref.[4],the authors considered large scale structure formation in EiBI gravity and investigated the linear matter power spectrum.In Ref.[5],the authors considered black hole solution and strong gravitational lensing in EiBI gravity.For more details about EiBI gravity,see Refs.[6-10].

The idea of extra dimensions opens a new way to solve some long-standing problems in high-energy physics and phenomenology,such as the gauge hierarchy problem and the cosmological constant problem.[11−14]The extra dimension arised in the very early 1920’s by Kaluza and Klein(KK)with assuming that the photon field originates from fifth component of a five-dimensional metric tensor.[15−16]In their approach,the extra dimension is compactified into the topology of S1,and the compact-ification radius is taken to be the Planck scale. The KK theory opens the way to investigate higher dimensional theory and achieves a purely geomtrical unification of gravity with electromagnetism.However,KK’s theory had not drawn enough attention until the late 1970’s and 1980’s with the developments of superstring theories. The brane-world was proposed during the early 1980s,[17−18]and had made great progress after the Arkani–Hamed–Dimopoulos–Dvali(ADD)model[11]and Randall–Sundrum(RS)model.[13−14]The ADD model predicts the deviations from the 4D Newton law at submillimeter distances,where the extra dimension of the ADD model is flat and compact.While the RS model has an in finite extra dimension using a wraped geometry,which suggests that the ordinary matter and interaction is trapped on a four-dimensional hypersurface embedded in a higher-dimensional space-time.There has been increasing interest focused on the study of brane-world scenario during recent years.[19−34]

For all these models,it is important to describe how to localize various bulk matter fields on the brane by a natural mechanism.In many brane-world models the massless scalar fields can be trapped on the branes.[35−36]Usually,spin-1 Abelian vector fields can not be localized on fivedimensional flat branes.[37]But,it can be localized on the RS brane in higher dimensional case[38]or on the thick dS brane and Weyl thick brane.[39]Generally,without the scalar-fermion coupling,fermions do not have normalizable zero modes in five dimensions.[39−41]Fermions can escape into the bulk by tunnelling,and whose rate de-pends on the parameters of the scalar potential.[42]In Ref.[43],for a two-scalar-generated Bloch brane model,a simple Yukawa coupling between two scalars and a spinor field was considered.[44]This research about brane world motivates us to investigate the interesting problem that whether high dimensional fermionic field can be localized on a new membrane,i.e.,the EiBI brane.

In a recent work of Ref.[45],the authors investigated the stability problem of gravitational perturbations for a more general EiBI braneworld.There are two typical brane models,and in one case,the brane solution does not support inner brane structure.While,in the other model,the interesting brane solution has inner structure and some gravitational resonances exist.In this paper,our goal is to extend the idea of Ref.[45]to obtain the understanding of the resonance of fermions in the EiBI brane.The background scalar field with an assumed relation φ′(y)=K1a(y)2(1 − K2a(y)2)is included in the if ve-dimensional bulk to generate the smooth thick brane con figuration,where the scalar field has kink,double kink,or anti-kink solution.So one can expect that the localization of fermion on the EiBI brane can present some appealing features.Massive KK states of the resonant fermion with finite lifetime will appear,and the continuous gapless states with m2>0 are derived.Fermionic resonances for right and left chiralities are obtained,and their appearance is related to branes with inner structure.Only the left-chial or right-chiral fermionic zero mode,i.e.,the 4D massless fermionic field can be localized on this brane with Yukawa coupling term,however,the massive KK states of fermion can not be localized on the brane.We analyze the effect of the parameter K2in the model on the localization of fermions,including the resonant study for lifetime τ,relative probability P,and effective potential Veffof massive KK fermions.

The plan of this work is the following:In Sec.2,we review the general aspects of the EiBI theory.In Sec.3,the localization of fermionic zero mode on this solution is given in detail.In Sec.4,we analyze the resonance of the massive fermion KK modes.Finally,conclusion and discussion are presented.We use units where G=c=1 unless otherwise noted.

2 The Model

We start with the following action of the EiBI theory in d-dimensional spacetime[46]

where κ =8πGdwith Gdthe d-dimensional Newtonian gravitational constant,b is a parameter with mass dimension 2,λ is a dimensionless constant associated with the cosmological constant Λ as λ =1+kΛ (Ref.[1]for the detail).In EiBI,the connection field Γ is independent of the metric,and RMN(Γ)is the Ricci tensor evaluated solely by the connection Γ.SM[g,φ]is the action for the matter which is coupled only to the gravitational field gMN.The theory follows the Palatini formalism in which the metric gMNand the connectionare treated as independent fields.

A brane-world model with a scalar field exists in the background as the material to construct the brane configuration.The full action is taken as the EiBI action(1)with the matter part given by a scalar field:

where V(φ)is the scalar potential.In the general metricaffine EiBI gravity,the matter action depends on the connection SM=SM(g,Γ,φ).

Note that when there is no cosmological constant(Λ =(λ−1)/κ =0),the asymptotically flat solutions are obtained when λ=1.The EiBI action(1)is equivalent to a bimetric-like theory action

The equations of motion by varying the action(1)with respect to the metric gMNand the connection Γ are written as follows:

where TMNis defined as the standard energy momentum tensor:TMNwith indices lowered by the metric gMN.The energy-momentum conservation equation∇MTMN=0 for matter fields in the EiBI theory is held as in GR,where the covariant derivative is compatible with the metric gMN.While qMNis an auxiliary metric and compatible with the connection Γ,i.e.,=(1/2)qKL(qLM,N+qLN,M−qMN,L)is the Christo ff el symbol of the auxiliary metric.

We are interested in the static flat brane with fourdimensional Lorentz invariance,for which the ansatz for the metrics are[14]

where the brane coordinate indices µ,ν =1,2,3,4 and ηµν=diag(−1,+1,+1,+1),and the function a(y)in the above metric is the so-called warp factor.

The equation of motion for the scalar field can be derived from(2):

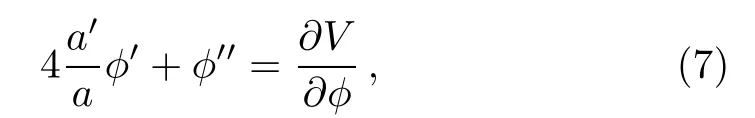
and the energy-momentum tensor is given by

where the prime denotes the derivative with respect to the extra dimension y.

By considering the spacetime metric(6)and the auxiliary metric qMN=(−u,u,u,u,v),the equations of motion(5)are read as

Here u and v are the functions of the extra dimension y.Then,with the explicit forms of the energy-momentum tensor(8)and the auxiliary metric,Eqs.(9a)and(9b)are reduced to

where Λ±= λ +bκV ± (1/2)φ′2.

There are three variables a(y),φ(y),and V(φ)obeying the three equations(7),(9a),and(9b),respectively.However,because of the conservation of the energy-momentum,the three equations are not independent and the system cannot be solved uniquely.Therefore,we need to introduce a relation between these variables or give the assumption of one of the three variables.In Ref.[45],a generalized relation φ′(y)=K1a(y)2(1 − K2a(y)2)was proposed,where the parameter K1can be fixed,and K2is a free parameter.Here we still use this relation and solve the equations of motion of fermions numerically.Then,Eq.(7)can be easily solved as

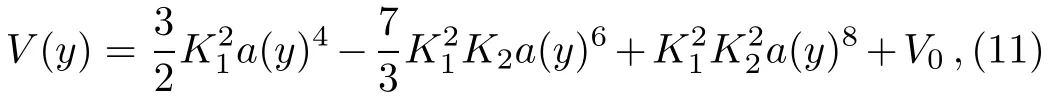
where the integral constant V0represents the scalar vacuum energy density.Thus,Eq.(10)can be expressed as

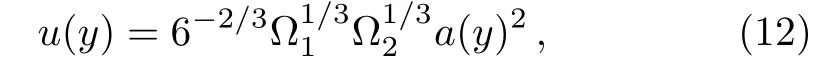
where

and the parameter=λ+bκV0.We can fix the integral constant V0by setting=0 to simplify the calculation,namely,V0= −λ/bκ.

Then,the auxiliary metric can be simplified as

where the parameter α =bκ.Equation(9)can be solved numerically with the following two initial conditions:

which will lead to even-parity and odd-parity KK modes,respectively.

Fig.1 (Color online)The shapes of the wrap factor a(y)and the scalar φ(y),the energy density ρ(y),the scalar potential V(y).The parameters are set to b=1,κ =1,λ =1.The red dashed line is for K2= −2.The blue thick dashed line is for K2=0.99.The green thick line is for K2=1.01.The blue thin line is for K2=2.

The shapes of the warp factor a(y),the scalar field φ(y),the energy density ρ(y)and the scalar potential V(y)are shown in Fig.1.It can be seen that the wrap factor becomes fatter first and then thinner with the increase of K2.When K2=2,the wrap factor suddenly becomes narrow.On the other hand,the scalar field is a single kink solution with K2=−2 far away from the critical value=1,and has a double kink solution with K2→1.The shapes of the scalar field have the opposite direction with K2=2,where the value of φ is positive when y→ −∞ and negative when y→+∞,which is opposite from the usual kink situation and denotes an anti-kink solution.The scalar field with K2=1.01 or K2=0.99 has a double kink configuration,which corresponds to a flat brane with inner structure:a volcano-like shape with two potential wells,and such brane with inner structure may support resonant KK modes for fermionic fields.Interestingly,the shape of the scalar field changes from a kink solution to an antikink solution with increasing parameter K2.This feature will affect the localization of zero fermion mode,as we will see in the next section.

3 The Localization of Fermions

In general,if one does not introduce the coupling between the fermion and scalars,a bulk fermion does not have a normalizable zero mode in five dimensions.So we introduce the simplest Yukawa coupling η¯ΨφΨ,and explore localization of a spin-1/2 fermion on the flat brane generated by the background scalar field.This situation is similar to the one in Refs.[36,47-52],in which the authors introduced the Yukawa coupling term η¯ΨF(φ)Ψ for the localization of the fermion fields on a brane.In the following,we turn to investigate the EOM of fermions,the zero mode of spin-1/2 fermions,and their lifetime of quasi-localized fermions on EiBI brane.

3.1 A Brief Review of Fermion

Initially we take the action of a Dirac fermion coupled to the background scalar φ[36,47−48]

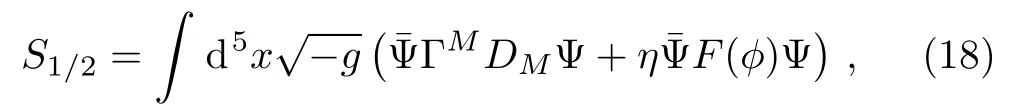
where DMΨ =(∂M+ ωM)Ψ and η is a coupling constant.The sign of the coupling η of the spinor Ψ to the scalar φ is arbitrary and η represents the spinor field coupled to kink or to double-kink,and anti-kink domain wall.For definiteness,we shall take in what follows the value η>0.As is known,the Dirac matrices in curved space are ΓM=a−1(γµ,γ5),where γµare the usual 4 × 4 flat gamma matrices chosen in such a way that γ5is diagonal,i.e.,γ5=diag{1,−1}.The non-vanishing components of the spin connection ωMfor the background metric(6)are

withthe spin connection derived from the metric(x).Then,with the variation of the action in(18),we obtain the following Dirac equation

where γµ(∂µ+)is 4-dimensional Dirac operator on the brane.Here,we have utilized a coordinate transformation dy=a(z)dz.By performing the coordinate transformation dz=a−1(y)dy,one can change the metric(6)to a conformally flat one

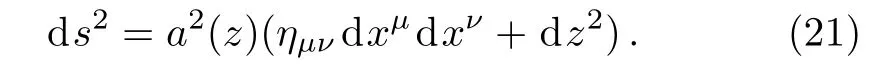
We now investigate the localization and resonance of the spin-1/2 spinor on the brane by studying the above Dirac equation.We expect that the left-and right-chiral projections of the four-dimensional part have different behaviors by considering the Dirac structure of the fifth gamma matrix γ5.Now we use the following chiral decomposition of the full 5-dimensional spinor

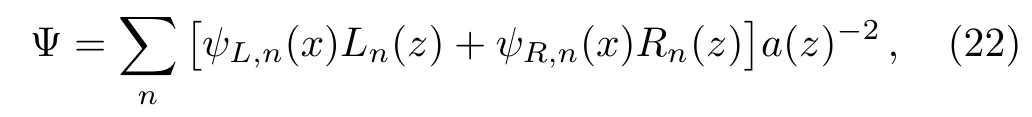
where ψL,nand ψR,n,satisfying ψL,n= −γ5ψL,n, ψR,n=γ5ψR,n,are the left-and right-chiral components of a four-dimensional Dirac field,respectively.In order to study the KK states of the scalar field we should rewrite the equation of motion(the part due to the extra dimension)in a Schrodinger-like equation.After inserting(22)into(20)and requiring that γµ(∂µ+)ψL,R=mψR,L,we arrive at the following Schr¨odinger-like equation for the z dependence:

where the effective potentials are

Because the effective potential functions have a Z2symmetry,the solutions of the Schr¨odinger equations(24a)and(24b)with even parity and odd parity will be obtained for the above two initial conditions,respectively.The above equations(23a)and(23b)can be recast into the supersymmetric quantum mechanics form,so the tachyonic KK modes are excluded.

We can decompose the action(18)into the actions for the massless and a series of massive left-chiral fermions

Going back to the action(18)we make again the procedure of separation of variables,one gets the action for a series of massive right-chiral fermions

The part dependent on the extra dimension in the action above will be determined by the left-chiral or rightchiral wave function resulting from the EiBI brane.By providing the following orthonormality conditions for Lnand Rnare satisfied:

the five-dimensional action can be reduced to the standard four-dimensional action

Equations(27),(28),and(29)are also the localization conditions for massless and massive KK modes of fermions.

From Eqs.(23)and(24),it is obvious that,in order to localize the left-and right-chiral fermions,there must be some kind of scalar-fermion coupling,or else the effective potential takes zero value,which will lead to the plane wave behavior for fermions describing the free propagation of particles in the bulk.Moreover,if we demand that VL(z)and VR(z)are Z2reflection symmetry z→ −z,F(φ)should be an odd function of the kink φ(z).In this paper,we choose the simplest Yukawa coupling:F(φ)= φ.Then the potentials for left-and right-chiral fermion can be expressed as

The values of potential(31)at z=0 and z→±∞are given by

As mentioned above,the background scalar field φ(z)has a single kink,a double kink or an anti-kink con figuration due to four different values of K2=−2,0.99,1.01,2.Thus φ′(0)has three possible values,namely, φ′(0)>0,=0,<0.Here we take the case φ′(0)>0 corresponding to a single-kink solution.And if the coupling η between the scalar and the fermion increases,a potential well around the location of the brane would emerge and the potential well would be deeper.We plot effective potentials VLand VRin Figs.3(a)and 3(c)for b=1,κ =1,λ =1 and K2=1.01,where both potentials tend to zero when z→ ±∞,but they have opposite behavior at the origin z=0.It can be seen that VL(z)and VR(z)in the corresponding Schr¨odinger equations are modified volcano-type potentials.Hence,the potential of left chiral fermions provides no mass gap to separate the zero mode from the excited KK ones,and there exists a continuous gapless spectrum of the KK modes for left chiral fermions.Moreove,it comes the same conclusion for right chiral fermions.The potential of right chiral fermions provides no mass gap and results in a continuous gapless right chiral KK modes.

3.2 The Zero Mode of Left and Right Chiral Fermion

From Eqs.(23)and(31)with m=0,we have

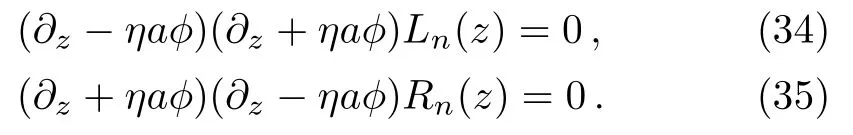
Then the left-and right-chiral fermion zero modes can be solved as

From the shapes of the warp factor and scalar φ,we have[Phys.Rev.D 90(2014)104007]a(z→ ±∞)→The asymptotic behavior of left-and rightchiral fermion zero mode can be analyzed[45]:

From Eq.(38),it is obvious that only one kind of fermion zero mode,left or right chiral feimion,can be localized on the brane.We need to further check whether the normalization condition(27)is satisfied for the left-chiral zero mode,i.e.,

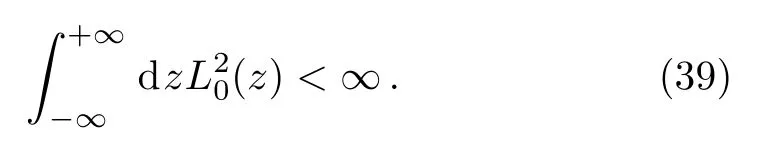
Since the values of the zero modes are finite at finite z,the above normalization condition is equivalent to the following condition

Only when η>(note that φ0and b are positive real parameters),the above integral is convergent,which means that the left-chiral zero mode can be localized on the brane under this condition.

Figure 2 shows that the value of the background scalar field φ at y→ +∞ changes from positive to negative with the increasing of parameter K2,namely,the value of φ0in Eq.(38)becomes negative with large K2.This feature will change the localization of left fermion zero mode into right fermion zero mode with a given coupling constant η,and vice verse.

The potential VRis always positive at the brane location and vanishes when far away from the brane with negative η.As we can observe,VR→ 0 when z→ ∞.This excludes the possibility of gaps.This means that the potential could not trap any bound right chiral fermions,namely,there is no zero mode of right chiral fermions.It agrees with the well-known fact that massless fermions must be single-handed in brane models.

Fig.2 (Color online)(a)is about the relation between the value of φ(+∞)and K2.(b)is φ(+∞)around K2=1.The other parameters are set to b=1,κ =1,and λ =1.

4 The Resonances of Fermions

As mentioned above,all the massive KK modes of the left-and right-chiral fermions are continuous and can not be localized on the brane.There could exist some resonant states at some m2.In order to investigate this possibility it is important to study the wave function Ln(z),Rn(z),for several eigenvalues m2,from the Schr¨odinger-like equation for KK modes of fermions(23a)and(23b).We can solve this equation numerically in order to better understand the presence of resonances.

By means of a numerical method,i.e.,Numerov method,[53−54]for a Schr¨odinger equation combined with the effective potential,the numerical results of Eqs.(23a)and(23b)give the corresponding fermion KK modes with a series of propabilities and lifetimes. Following the procedure of Refs.[45,47],we get some chiral fermion resonances corresponding to peaks in the relative probability PL,R(m2),which is a function of mass square of the fermion KK modes. When m2>VL,R(z)max(VL,R(z)maxis the maximum of the effective potential),the KK modes are approximately plane wave and hence the value of PL,R(m2)is of about zb/zmax=0.1.When m2

Table 1 The mass,width,and lifetime of resonances for fermions.The parameters are set to b=1,κ=λ=1 and K2=1.01.Here n is the order of resonant states with corresponding m2from small to large.

Here we choose η=1,the height of the potential of the massive chiral fermions will become large,then a series of massive fermion resonant states will appear.And we define the width Γ = △m of each resonant state as the width at the half maximum of a resonant peak.The lifetime for the resonant KK modes,which means that the fermion disappears into the extra dimension with time τ∼ Γ−1,are listed in Table 1.It is obvious that the first peak is the most narrow one,namely,the lifetime of this resonant state is the longest,but it decares with the increasing number n.So we can get the conclusion that the KK modes with a lower resonant state have a longer lifetime on the brane.

Fig.3 (Color online)The shapes of the potential of fermions and it’s resonance.The parameters are set to b=1,κ =1,λ =1,η =1 and K2=1.01.The red and dashed line is for even parity.The blue thin line is for odd parity.

The shapes of the probability PL,R(m2)of resonance states are shown in Figs.(3b)and(3d). Here,we only consider the resonances whose mass satisfy m2

Fig.4 (Color online)The shapes of the resonances L1,L2,L3,L4.The parameters are set to b=1,κ=1,λ=1,and K2=1.01.The red and dashed line is for odd parity function.The blue thin line is for even parity function.

Fig.5 (Color online)The shapes of the resonances R1,R2,R3,R4.The parameters are set to b=1,κ=1,λ=1 and K2=1.01.The red and dashed line is for odd parity function.The blue thin line is for even parity function.

5 Conclusion and Discussion

We have investigated the resonant properties of chiral fermion in EiBI gravity,based on the Palatini formalism,in which the metric gMNand the connection ΓMNPare assumed to be independent fields.We solve the Schr¨odinger equations for KK modes of fermions with the numerical potentials under two types of initial value conditions corresponding to the odd-and even-parity solutions,respectively.

When the parameter K2is treated as a variable,we find it influences the solution of the background scalar field and the localization of fermion zero mode.By increasing K2,the scalar field changes from a single kink,a double kink to an anti-kink configuration.When K2approaches the critical value,i.e.,K2→Kcri=1,the scalar field has a double kink configuration corresponding to a flat brane with inner structure,which results in some discrete and resonant KK modes.Furthermore,Fig.2 shows that the value of the background scalar field φ at y → +∞ changes from positive to negative value with the increase of K2,where K2takes four values K2=−2,0.99,1.01,2.This feature will change the localization of left fermion zero mode into right fermion zero mode with a given coupling η.

There is no bound KK mode for both left-and rightchiral fermion zero modes without scalar-fermion coupling.By introducing a proper Yukawa coupling F(φ)=φ,it is proved that under the localization condition η >the integral can be finite,i.e.,the left-chiral spin 1/2 fields also can be localized on the thick brane.However,the zero mode of right-chiral fermion cannot be localized on the brane at the same condition.From Figs.3(a)and 3(c),we find both the potentials of fermion KK modes are vanishing at the boundary of extra dimension.For the volcano-like potential,there exists just one bound zero mode(massless fermion observed on the brane)and a set of continuous massive modes.In Figs.3(b)and 3(d),such potentials lead to seven massive and quasi-localized KK modes,which can stay on the branes for a certain time and then escape into the extra dimension.Using the Numerov method,we get the wave functions of the resonance states and use them to calculate the probability and the lifetime of resonant states.

The number of resonant modes is related with the inner structure of the brane,and the resonant state with lower mass has a longer lifetime.Moreover,the mass spectra of left-and right-chiral fermion are nearly the same referring to Table 1.Therefore,the contributions of the inner brane structure in EiBI theory to the fermionic field resonant state are investigated.We can find some similar discussions in Refs.[41-42,44,56-58]for massive fermions or gravitons.

References

[1]M.Baados and P.G.Ferreira,Phys.Rev.Lett.105(2010)011101,[arXiv:1006.1769].

[2]M.Born and L.Infeld,Proc.R.Soc.Lond.A 144(1934)425.

[3]P.Pani,V.Cardoso,and T.Delsate,Phys.Rev.Lett.107(2011)031101,[arXiv:1106.3569].

[4]X.L.Du,K.Yang,X.H.Meng,and Y.X.Liu,Phys.Rev.D 90(2014)044054.

[5]S.W.Wei,K.Yang,and Y.X.Liu,Eur.Phys.J.C 75(2015)253.

[6]H.Sotani and U.Miyamoto,Phys.Rev.D 92(2015)044052.

[7]A.A.Potapov,R.Izmailov,O.Mikolaychuk,N.Mikolaychuk,M.Ghosh,and K.K.Nandi,JCAP 1507(2015)018.

[8]I.Cho and H.C.Kim,Phys.Rev.D 90(2014)024063.

[9]K.Yang,X.L.Du,and Y.X.Liu,Phys.Rev.D 88(2013)124037.

[10]P.Pani and T.P.Sotiriou,Phys.Rev.Lett.109(2012)251102.

[11]N.Arkani-Hamed,S.Dimopoulos,and G.R.Dvali,Phys.Lett.B 429(1998)263,[arXiv:hep-ph/9803315].

[12]I.Antoniadis,N.Arkani-Hamed,S.Dimopoulos,and G.R.Dvali,Phys.Lett.B 436(1998)257,[arXiv:hepph/9804398].

[13]L.Randall and R.Sundrum,Phys.Rev.Lett.83(1999)3370,[arXiv:hep-ph/9905221].

[14]L.Randall and R.Sundrum,Phys.Rev.Lett.83(1999)4690,[arXiv:hep-th/9906064].

[15]T.Kaluza,Sitzungsber.Preuss.Akad.Wiss.Berlin(Math.Phys.)K1(1921)966.

[16]O.Klein,Z.Phys.37(1926)895.

[17]K.Akama,Lect.Notes Phys.176(1983)267,[arXiv:hepth/0001113].

[18]V.A.Rubakov and M.E.Shaposhnikov,Phys.Lett.B 125(1983)136.

[19]W.D.Goldberger and M.B.Wise,Phys.Rev.Lett.83(1999)4922,[arXiv:hep-ph/9907447].

[20]M.Gremm,Phys.Lett.B 478(2000)434,[arXiv:hepth/9912060].

[21]M.Gremm,Phys.Rev.D 62(2000)044017,[arXiv:hepth/0002040].

[22]O.DeWolfe,D.Z.Freedman,S.S.Gubser,and A.Karch,Phys.Rev.D 62(2000)046008,[arXiv:hep-th/9909134].

[23]C.Csaki,J.Erlich,T.J.Hollowood,and Y.Shirman,Nucl.Phys.B 581(2000)309,[arXiv:hep-th/0001033].

[24]T.Gherghetta and A.Pomarol,Nucl.Phys.B 586(2000)141,[arXiv:hep-ph/0003129].

[25]N.Arkani-Hamed,M.Porrati,and L.Randall,J.High Energy Phys.0108(2001)017,[arXiv:hep-th/0012148].

[26]A.Campos,Phys.Rev.Lett.88 (2002)141602,[arXiv:hep-th/0111207].

[27]S.Kobayashi,K.Koyama,and J.Soda,Phys.Rev.D 65(2002)064014,[arXiv:hep-th/0107025].

[28]A.Wang,Phys.Rev.D 66(2002)024024,[arXiv:hepth/0201051].

[29]C.Charmousis,S.C.Davis,and J.F.Dufaux,J.High Energy Phys.0312(2003)029,[arXiv:hep-th/0309083].

[30]D.Bazeia and A.R.Gomes,J.High Energy Phys.0405(2004)012,[arXiv:hep-th/0403141].

[31]Y.X.Liu,L.Zhao,X.H.Zhang,and Y.S.Duan,Nucl.Phys.B 785(2007)234,[arXiv:0704.2812].

[32]V.Dzhunushaliev,V.Folomeev,and M.Minamitsuji,Phys.Rev.D 79(2009)024001,[arXiv:0809.4076].

[33]V.Dzhunushaliev,V.Folomeev,B.Kleihaus,and J.Kunz,J.High Energy Phys.1004(2010)130,[arXiv:0912.2812].

[34]Y.X.Liu,Y.Zhong,Z.H.Zhao,and H.T.Li,J.High Energy Phys.1106(2011)135,[arXiv:1104.3188].

[35]D.Langlois and M.Sasaki,Phys.Rev.D 68(2003)064012.

[36]D.Bazeia,A.R.Gomes,L.Losano,and R.Menezes,Phys.Lett.B 671(2009)402.

[37]I.Oda,Phys.Lett.B 496(2000)113.

[38]Y.X.Liu,Z.H.Zhao,S.W.Wei,and Y.S.Duan,JCAP 0902(2009)003.

[39]Y.X.Liu,X.H.Zhang,L.D.Zhang,and Y.S.Duan,J.High Energy Phys.0802(2008)067.

[40]B.Bajc and G.Gabadadze,Phys.Lett.B 474(2000)282.

[41]Y.Grossman and N.Neubert,Phys.Lett.B 474(2000)361.

[42]S.L.Dubovsky,V.A.Rubakov,and P.G.Tinyakov,Phys.Rev.D 62(2000)105011.

[43]C.A.S.Almeida,R.Casana,M.M.Ferreira Jr.,and A.R.Gomes,Phys.Rev.D79(2009)125022.

[44]D.Bazeia,M.J.dos Santos,and R.F.Ribeiro,Phys.Lett.A208(1995)84.

[45]Q.M.Fu,L.Zhao,K.Yang,B.M.Gu,and Y.X.Liu,Phys.Rev.D 90(2014)104007.

[46]D.N.Vollick,Phys.Rev.D 69(2004)064030.

[47]Y.X.Liu,J.Yang,Z.H.Zhao,C.E.Fu,and Y.S.Duan,Phys.Rev.D 80(2009)065019;Y.X.Liu,C.E.Fu,L.Zhao,and Y.S.Duan,Phys.Rev.D 80(2009)065020.

[48]T.R.Slatyer and R.R.Volkas,J.High Energy Phys.0704(2007)062;R.Davies,D.P.George,and R.R.Volkas,Phys.Rev.D 77(2008)124038.

[49]I.Oda,Phys.Lett.B 496(2000)113.

[50]C.Ringeval,P.Peter,and J.P.Uzan,Phys.Rev.D 65(2002)044016.

[51]Y.X.Liu,X.H.Zhang,L.D.Zhang,and Y.S.Duan,J.High Energy Phys.0802(2008)067;Y.X.Liu,L.D.Zhang,L.J.Zhang,and Y.S.Duan,Phys.Rev.D 78(2008)065025.

[52]Z.H.Zhao,Y.X.Liu,and H.T.Li,Class.Quantum Grav.27(2010)185001.

[53]B.V.Numerov,Roy.Ast.Soc.Monthly Notices 84(1924)592.

[54]D.Bazeia,A.R.Gomes,and L.Losano,arXiv:0708.-3530[hep-th].

[55]Y.X.Liu,H.T.Li,Z.H.Zhao,J.X.Li,and J.R.Ren,J.High Energy Phys.0910(2009)091.

[56]C.A.S.Almeida,R.Casana,M.M.Ferreira,and A.R.Gomes,Phys.Rev.D 79(2009)125022.

[57]S.Mouslopoulos,J.High Energy Phys.0105(2001)038.

[58]P.M.Llatas,Phys.Lett.B 514(2001)139.