Extracting Structure Parameters of Dimers for Molecular Tunneling Ionization Model∗

Song-Feng Zhao(赵松峰), Fang Huang(黄方),Guo-Li Wang(王国利),and Xiao-Xin Zhou(周效信)

College of Physics and Electronic Engineering,Northwest Normal University,Key Laboratory of Atomic and Molecular Physics and Functional Materials of Gansu Province,Lanzhou 730070,China

1 Introduction

With the rapid advancement of the field-free molecular alignment and orientation techniques,[1−4]tunneling ionization of molecules in a low-frequency strong laser field has been widely studied for more than a decade both experimentally[5−21]and theoretically,[22−30]especially for the angular dependence of ionization rate(or probability)P(θ)(θ is the angle between the molecular axis and the laser’s polarization direction)and ionization suppression of molecule in comparison to its companion atom.This is because tunneling ionization of molecules is the first fundamental step of many interesting strong- field rescattering phenomena such as high-order harmonic generation(HHG),high-energy above-threshold ionization(HATI)and nonsequential double ionization(NSDI).[31−33]

Experimentally,P(θ)has been determined by ionizing a partially aligned molecules.[5,8−10,15,19]Usingcold targetrecoilion momentum spectrometer(COLTRIMS),[34]the P(θ)can also be obtained by measuring the molecular frame photoelectron angu-lar distribution (MFPAD)[11−13,20−21]orby detecting the angular distribution of the emitted ionic fragments.[6−7,14,16−18]Theoretically,P(θ)has been obtained by using the single-active-electron approximation based time-dependent Schr¨odinger equation(SAETDSE),[23−25,35−39]time-dependent density functional theory(TDDFT),[22,40−43]or time-dependent Hatree–Fock(TDHF).[44]These ab-initio calculations are still quite challenging even for the simpler linear molecules.Therefore,some theoretical models are desirable especially for interpreting the experimental measurement of tunneling ionization of molecules in a strong laser field,such as the molecular Ammosov–Delone–Krainov(MOADK),[26−27,45−49]the molecular strong- field approximation(MO-SFA),[28−29]the molecular Perelomov–Popov–Terent’ev(MO-PPT),[50−51]and the weak- field asymptotic theory(WFAT).[30,52−55]

Ionization suppression is another very interesting strong- field phenomena.Since tunneling ionization rate sensitively depends on the ionization potential(IP)of atoms(or molecules),one may expect the ionization rate should be comparable for a molecule and its companion atom.[56−58]However,it has been experimentally found that the ionization is strongly suppressed for the cases of D2(IP of 15.47 eV),O2(IP of 12.03 eV),and Cl2(IP of 11.48 eV)in comparison to their closest companion atoms Ar(IP of 15.76 eV)and Xe(IP of 12.13 eV),respectively,while there is no suppression for N2(IP of 15.58 eV)and F2(IP of 15.70 eV)when compared with their companion Ar atom.[50,59−64]Several theoretical models,such as Keldysh–Faisal–Reiss(i.e.MO-SFA),[28]MO-ADK,[26]multielectron screening,[65]have been proposed to interpret the experimental measurements.So far,MO-ADK model agrees well with the experimental results for pairs with suppression(D2:Ar,O2:Xe,Cl2:Xe)and pairs without suppression(N2:Ar,CO:Kr).However,the MO-ADK model predicts there is ionization suppression for F2:Ar,which is in disagreement with experiment.

In this paper,we determine and tabulate structure parameters of the highest occupied molecular orbital(HOMO)of 27 dimers for the MO-ADK model using our previous proposed method[27,48,66−67]in Sec.3.We will also show the ionization probability of a rare-gas dimer Ne2,which has a full- filled antibond valence orbital(σu),is strongly suppressed when compared with that of its closest companion Ne atom.The rest of this paper is arranged as follows.In Sec.2,we will present how to numerically calculate molecular potentials using the density function theory(DFT)and obtain the molecular orbital wave functions with correct asymptotic behavior by solving time-independent Schr¨odinger equation with B-spline functions.The basic equations of MO-ADK,MO-PPT and MO-SFA models are also briefly reviewed.A conclusion will be given in Sec.4.Atomic units are used throughout this paper unless otherwise stated.

2 Theoretical Method

2.1 Construction of the One-Electron Potentials of Linear Molecules

There are two main approaches to obtain the molecular orbital wave functions with the correct asymptotic behavior,namely using X2DHF program only for diatomic molecules[47]or by solving the time-independent Schr¨odinger equation of any linear molecules of interest.In the second method,one can easily include the exchangecorrelation interaction in molecular potentials[66−67]by using the LBα model.[68−69]

Under the single-center expansion,the one-electron potentials of linear molecules can be expressed as

where vl(r)is the radial component of the potential and Pl(cosθe)is the Legendre polynomial. θeis the angular coordinate of the active electron in the molecular frame.We take lmax=80 for He2,Ne2,Mg2,Si2,P2,and Ar2,lmax=120 for K2,Ca2,V2,Cr2,Mn2,Fe2,Co2,Cu2,Zn2,Ge2,As2,Se2and Kr2,and lmax=150 for others,respectively.The radial potential can be written as

where the first two terms are the electrostatic potential(see Refs.[48,70]and the last term describes the exchange-correlation interaction(see Ref.[66]).

2.2 Calculation of Molecular Wave Functions by Solving the Time-Independent Schr¨odinger Equation

With molecular potentials calculated numerically using the method described in Subsec.2.1,we can obtain molecular wave functions with the correct asymptotic behavior by solving the following time-independent Schrdinger equation of linear molecules[27,48,66−67]

Due to the cylindrical symmetry,the wave function(r)can be written as

with ξ=cosθeand χeis the angular coordinate of the active electron in the molecular frame.The wave function ψ(r,ξ)can be expanded by B-spline functions as

Here,Bi(r)and Bj(ξ)are radial and angular B-splines,respectively.Typically we take the corresponding number of angular B-splines Nξ=30 and of radial B-splines Nr=80 for six smaller molecules(i.e.,He2,Ne2,Mg2,Si2,P2and Ar2)and Nr=150 for others,respectively.By substituting Eqs.(1),(4)and(5)into Eq.(3)and then projecting onto the Bi′(r)(1 − ξ2)|m|/2Bj′(ξ)basis,we obtain the following matrix equation

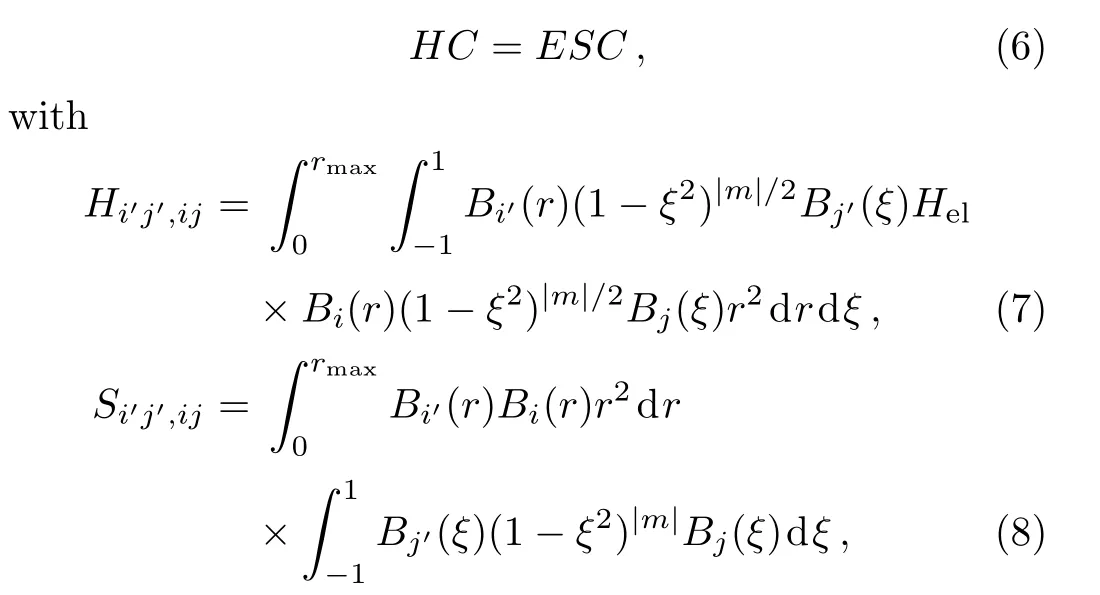
where E and C are energy and coefficient matrices,respectively.The eigenfunctions and eigenvalues can be obtained by diagonalizing Eq.(6).

Based on the single-center expansion,the wave functions of the ionizing orbitals of a linear molecule can be expanded as

where Ylm(θe,χe)is the spherical harmonic functions.The radial wavefunction can be calculated by

Then accurate structure parameters Clmcan be determined by matching these radial functions to the following form in the asymptotic region

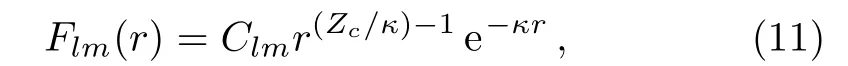
where Zcis the asymptotic charge andis the ionization potential of molecules.

2.3 MO-ADK,MO-PPT and MO-SFA Models

Once the structure parameters and ionization potential of molecules are available,one can easily calculate the cycle-averaged ionization rate using the MO-ADK model[26]as follows

where F is the field strength and B(m′)can be given by

where R is the Euler angles of the molecular frame with respect to the laboratory fi xed frame.is the rotation matrix and

It is known that the MO-ADK model works well in the tunnelling ionization region,while it fails to give accurate ionization rate in the multiphoton region.It has been con firmed that the MO-PPT model can fit the experimental data and SAE-TDSE results in the whole range covering from multiphoton to tunnelling regimes.[51]Based on the MO-PPT model,[50−51]the cycle-averaged ionization rate can be expressed as

where γ is Kelydsh parameter and g(γ)can be written as

In Eq.(15),the coefficients Am′(ω,γ)can be found in Refs.[71–73].For an atom,Eq.(15)can be reduced as

where Clis structure parameter of atom.

Using the cycle-averaged ionization rates,the total ionization probability of a molecule by a laser pulse can be calculated by

where m stands for the PPT,the MO-ADK or the MOPPT model.For a Gaussian pulse,the envelope F(t)can be expressed as

with F0being the peak strength of a laser pulse and τ is the full width at half maximum(FWHM).

According to the MO-SFA theory,[67,74]the total ionization probability of molecules by a laser pulse can be expressed as

where the ionization amplitude f(p,R)is given by

with p being the momentum of the emitted electron.E(t)and A(t)are the electric field and the vector potential,respectively.The quasiclassical action S(p,t)is written as

In Eq.(21),the ground-state electronic wave function Φ0(r)of molecules is obtained from the GAUSSIAN package[75]and the continuum state is approximated by a Volkov state.

3 Results and Discussion

3.1 The One-Electron Potentials for Ar2

We numerically calculate the one-electron potentials of linear molecules based on the DFT which described in Subsec.2.1,where the initial wave functions of all the occupied molecular orbitals are obtained from GAUSSIAN.[75]Figure 1 shows partial wave expansions(r),(r),(r),and vl(r))of the potential V(r,θe)(see Eqs.(1)and(2))for Ar2.

Fig.1 (a)Partial electron-nucleus potential;(b)partial electron-electron repulsion potential;(c)partial exchangecorrelation potential;(d)partial total potential.We use lmax=80(see Eq.(1))for Ar2,but we only show here the l=0,2,4,6,8 terms for clarity.

3.2 Determination of Structure Parameters of the HOMO for 27 Selected Dimers

Once molecular potentials are constructed numerically,wave function and the corresponding ionization potential of linear molecules can be determined by solving Eq.(3).In Table 1,we compare the ionization potentials calculated using the present LBα model with the experimental vertical ionization potentials.For Xe2,the calculated ionization potential with GAUSSIAN code[75]using Hatree–Fock(HF)method and 3-21G basis set is also given for reference because the experimental value is unavailable as far as we know.The internuclear distances of these molecules are also listed.In the LBα model,[68]there are two empirical parameters α and β.In our calculations,we take β =0.01 and α is optimized to obtain accurate ionization potential,which is also tabulated in Table 1.With wave functions and ionization potentials,we can extract molecular structure parameters in the asymptotic region(see Eqs.(10)and(11)).In Table 2,we tabulate the structure parameters of the HOMO for 27 selected dimers.We emphasize that these structure parameters should be essential to calculate the ionization rate with the MO-ADK or the MO-PPT model.

3.3 Comparison of Alignment-Dependent Ionization Probabilities Between the MO-ADK and the MO-SFA Models

It is known that the alignment-dependent ionization probability P(θ)can be used to image directly electronic structures of the ionizing orbital from which the active electron is removed.By far,there is no experimental and more accurate theoretical P(θ)can be used to check the MO-ADK result.Next,we will examine the P(θ)from the MO-ADK by comparing with that of the MO-SFA.Based on the MO-ADK model,the P(θ)can be easily calculated according to Eq.(18)by using ionization potentials and structure parameters tabulated in Tables 1 and 2,respectively.Figure 2 shows the P(θ)of Cu2,Mg2,Se2and As2,respectively.All the ionization probabilities are normalized to 1.0 at the peak for simplicity.It is clear that the P(θ)obtained from the MO-ADK agree generally with that of the SFA.For Cu2and Mg2,the HOMO is a σgand σuorbital,respectively.The P(θ)is expected to have a peak at 0◦and a minimum at 90◦.We can see that the P(θ)exhibits a peak at 0◦and a minimum at 90◦in deed.For Se2,the HOMO is a πgorbital,the correspond-ing P(θ)is expected to have a peak at 45◦.However,the MO-ADK and the MO-SFA results show a peak at 35◦and 40◦,respectively.For As2,the HOMO is a πuorbital and a peak at 90◦is expeceted,while the P(θ)from both the MO-ADK and MO-SFA tend to have a peak near 50◦and a minimum at 90◦.

Fig.2 Normalized angular dependence of ionization probability.(a)Cu2at laser intensity of 1.6×1013W/cm2;(b)Mg2at 8.0×1012W/cm2;(c)Se2at 2.5×1013W/cm2;(d)As2at 3.4×1013W/cm2.We take the laser field to be a Gaussian pulse with central wavelength of 800 nm and FWHM of 10 fs.

Table 1 Internuclear distances,ionization potentials calculated with the present LBα model and experimental vertical ionization potentials for 27 dimers.The internuclear distances and experimental vertical ionization potentials are from Smirnov et al.[76]For Xe2,the calculated ionization potential with GAUSSIAN code[75]using Hatree-Fock(HF)method and 3–21G basis set is also given because the experimental one is unavailable.The α parameter used in the LBα model is also listed.

Table 2 Fitted Clmcoefficients using the LBα potentials for 27 selected dimers.Note that m=0,1 and 2 for σ,π and δ,respectively.

3.4 Laser Wavelength Dependence of Ionization Rates from Several Selected Dimers

It is found that ionization probabilities of atoms and molecules in a laser field depend sensitively on the laser wavelength especially in the multiphoton ionization region.[51,63−64,77]Based on the MO-PPT model,we will show how the intensity-and alignment-dependent ionization rates of dimers depend on the laser wavelength,respectively.Figure 3 shows the intensity-dependent ionization rates of Ar2at four different laser wavelengths.We can see that the ionization rate obtained from the MO-PPT model exhibits strong wavelength dependence.For a fixed laser intensity,the ionization rate increases monotonously as wavelength decreases.For the case of wavelength λ=2000 nm,the tunnelling ionization regime dominates and the ionization rate is close to the MOADK result.Actually,the ionization rate from the MOPPT should be equal to that of the MO-ADK because Am′(ω,γ) → 1,(1+ γ2)|m′|/2+3/4→ 1 and g(γ) → 1 in the limit of γ → 0.In the case of λ =600 nm,the multiphoton regime dominates in the intensity region shown in Fig.3.There is very large discrepancies between the MO-PPT and MO-ADK models.That is because the tunnelling ionization(i.e.,MO-ADK)model is invalid in the multiphoton region as we know.

In Fig.4,we show the alignment dependence of ionization rates for four dimers with different orbital symmetries.Based on the MO-PPT model,we found that the alignment dependent ionization rate P(θ)of these four dimers does not depend laser wavelength in the tunnelling ionization region(γ<1)as expected.We note that the P(θ)calculated from the MO-PPT is almost the same as that of the MO-ADK in the tunnelling ionization region.Can this conclusion still hold in the multiphoton ionization region(γ >1)?For Cu2,the HOMO is a σgor-bital,P(θ)does not exhibit laser wavelength dependence in the multiphoton ionization region where the wavelength λ <475 nm.For Mg2,the HOMO is a σuorbital,we can see that P(θ)has a slight dependence when λ <475 nm.For Se2,the HOMO is a πgorbital,there is a strong wavelength dependence of P(θ)shown in Fig.4(c),namely the angular width increases rapidly as the laser wavelength decreases from 475 nm to 400 nm and the peak position is shifted gradually toward smaller alignment angles.For As2,the HOMO is a πuorbital,the angular width of P(θ)displays a wavelength dependence,i.e.the width decreases rapidly from 475 nm to 450 nm and then increases gradually from 450 nm to 400 nm.

Fig.3 Intensity-dependent ionization rates at different laser wavelengths for Ar2.

Fig.4 Normalized alignment dependence of ionization rate at different laser wavelengths.(a)Cu2at laser intensity of 1.6×1013W/cm2;(b)Mg2at 8.0×1012W/cm2;(c)Se2at 2.5×1013W/cm2;(d)As2at 3.4×1013W/cm2.

3.5 Strong Ionization Suppression of Several Dimers Having Valence Orbital with Antibonding Systems

Finally,based on the PPT and MO-PPT models,we will turn to study the ionization suppression of molecule in comparison to its companion atom.In Fig.5,we show ionization probabilities of Cl2,Xe,Ne2and Ne.In our calculations,we treat all the molecules to be randomly aligned and a Gaussian pulse with wavelength of 800 nm and FWHM of 25 fs is used.For Cl2,it has a full- filled antibond valence orbital(πg),there is no companion atom in nature and the closest one is Xe.Although the ionization potential of Cl2(11.48 eV)is smaller than that of Xe(12.13 eV),we can still see that Cl2shows strong ionization suppression in comparison to Xe as shown in Fig.5(a),which is consistent with the prediction in Ref.[50].For F2,we also found the strong ionization suppression compared with its companion Ar atom(not shown),which is disagree with available experimental observations.In Fig.5(b),we see that there is strong ionization suppression of a rare-gas dimer Ne2(IP of 20.4 eV),which has a full- filled antibond valence orbital(σu),in comparison to its closest companion Ne atom(IP of 21.56 eV).Unfortunately,there is no available experimental results and more accurate theoretical simulations to compare with.

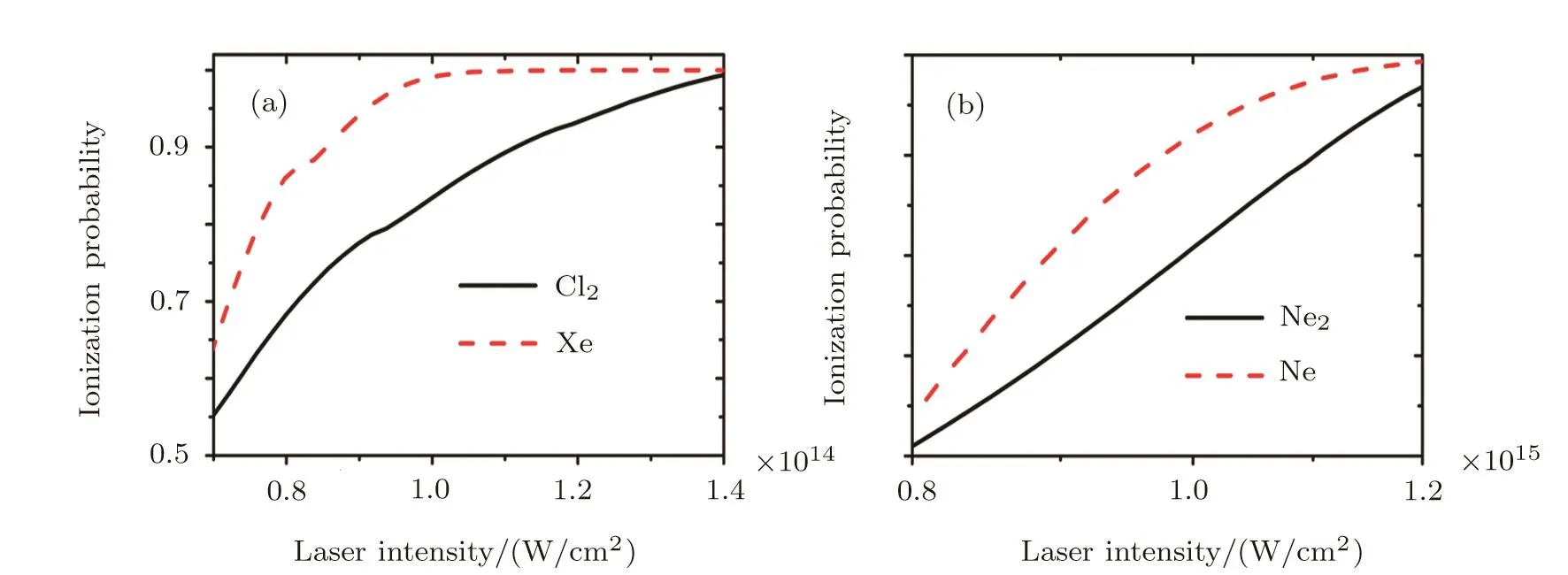
Fig.5 Ionization probabilities for two selected dimers and their corresponding closest companion atoms.(a)Cl2 and Xe;(b)Ne2and Ne.We use the laser field to be a Gaussian pulse with central wavelength of 800 nm and FWHM of 25 fs in the present calculations.

4 Conclusions

In this paper we determine structure parameters Clmin the MO-ADK model for the HOMO of 27 selected dimers,where wave functions with the correct asymptotic behavior are obtained by solving time-independent Schr¨odinger equation of linear molecules with B-spline functions and one-electron potentials,which are numerically created with the LBα model based on the DFT.We emphasize that these structure parameters should be useful and thus tabulated for future applications.Using the MO-ADK model,we study the alignment-dependent ionization probabilities of several selected dimers and compare them with the MO-SFA calculations.With rapid development of free-electron laser,it becomes reliable to ionize a valence electron(or an inner-shell electron)from atoms or molecules by absorbing a single or several highenergy photons.In this case,we propose to use the MOPPT model for studying the ionization of molecules since the MO-ADK model is invalid in the multiphoton ionization region.Based on the MO-PPT model,we found that ionization rate of molecules depends on the laser wavelength and two diatomic molecules having valence orbital with antibonding systems(i.e.,Cl2and Ne2)show strong ionization suppression in comparison to their corresponding closest companion atoms.It is of interest to see if the ionization suppression of Ne2compared with Ne atom can be observed by the future experiments and by more accurate theoretical simulations.More importantly,by including Ne2in the single ionization suppression investigations,we expect to shed more light on the ionization suppression issue of the puzzling F2.

References

[1]H.Stapelfeldt and T.Seideman,Rev.Mod.Phys.75(2003)543.

[2]J.G.Underwood,Nat.Phys.5(2009)253.

[3]O.Ghafur,A.Rouz´ee,A.Gijsbertsen,et al.,Nat.Phys.5(2009)289.

[4]M.Spanner,S.Patchkovskii,E.Frumker,and P.B.Corkum,Phys.Rev.Lett.109(2012)113001.

[5]I.V.Litvinyuk,K.F.Lee,P.W.Dooley,et al.,Phys.Rev.Lett.90(2003)233003.

[6]A.S.Alnaser,S.Voss,X.M.Tong,et al.,Phys.Rev.Lett.93(2004)113003.

[7]A.S.Alnaser,C.M.Maharjan,X.M.Tong,et al.,Phys.Rev.A 71(2005)031403(R).

[8]D.Pavii,K.F.Lee,D.M.Rayner,et al.,Phys.Rev.Lett.98(2007)243001.

[9]I.Thomann,R.Lock,V.Sharma,et al.,J.Phys.Chem.A 112(2008)9382.

[10]V.Kumarappan,L.Holmegaard,C.Martiny,et al.,Phys.Rev.Lett.100(2008)093006.

[11]A.Staudte,S.Patchkovskii,D.Pavii,et al.,Phys.Rev.Lett.102(2009)033004.

[12]H.Akagi,T.Otobe,A.Staudte,et al.,Science 325(2009)1364.

[13]M.Magrakvelidze,F.He,S.De,et al.,Phys.Rev.A 79(2009)033408.

[14]P.von den Ho ff,I.Znakovskaya,S.Zherebtsov,et al.,Appl.Phys.B 98(2010)659.

[15]R.Itakura,H.Hasegawa,Y.Kurosaki,et al.,J.Phys.Chem.A 114(2010)11202.

[16]X.Liu,C.Wu,Z.Wu,et al.,Phys.Rev.A 83(2011)035403.

[17]H.Liu,S.F.Zhao,M.Li,et al.,Phys.Rev.A 88(2013)061401(R).

[18]H.Chen,L.Fang,V.Tagliamonti,and G.N.Gibson,Phys.Rev.A 84(2011)043427.

[19]J.L.Hansen,L.Holmegaard,J.H.Nielsen,et al.,J.Phys.B 45(2012)015101.

[20]J.Wu,M.Meckel,S.Voss,et al.,Phys.Rev.Lett.108(2012)043002.

[21]J.Wu,L.Ph.H.Schmidt,M.Kunitski,et al.,Phys.Rev.Lett.108(2012)183001.

[22]S.K.Son and Shih-I.Chu,Phys.Rev.A 80(2009)011403(R).

[23]S.Petretti,Y.V.Vanne,A.Saenz,et al.,Phys.Rev.Lett.104(2010)223001.

[24]M.Spanner and S.Patchkovskii,Phys.Rev.A 80(2009)063411.

[25]M.Abu-samha and L.B.Madsen,Phys.Rev.A 80(2009)023401.

[26]X.M.Tong,Z.X.Zhao,and C.D.Lin,Phys.Rev.A 66(2002)033402.

[27]S.F.Zhao,C.Jin,A.T.Le,et al.,Phys.Rev.A 80(2009)051402(R).

[28]J.Muth-B¨ohm,A.Becker,and F.H.M.Faisal,Phys.Rev.Lett.85(2000)2280.

[29]T.K.Kjeldsen and L.B.Madsen,J.Phys.B 37(2004)2033.

[30]O.I.Tolstikhin,T.Morishita,and L.B.Madsen,Phys.Rev.A 84(2011)053423.

[31]C.D.Lin,A.T.Le,Z.Chen,et al.,J.Phys.B 43(2010)122001.

[32]M.Lein,J.Phys.B 40(2007)R135.

[33]S.Haessler,J.Caillat,and P.Sali`eres,J.Phys.B 44(2011)203001.

[34]J.Ullrich,R.Moshammer,R.D¨orner,et al.,J.Phys.B 30(1997)2917.

[35]G.Lagmago Kamta and A.D.Bandrauk,Phys.Rev.A 74(2006)033415.

[36]Y.J.Jin,X.M.Tong,and N.Toshima,Phys.Rev.A 83(2011)063409.

[37]B.Zhang,J.Yuan,and Z.X.Zhao,Phys.Rev.A 85(2012)033421.

[38]S.Petretti,A.Saenz,A.Castro,and P.Decleva,Chem.Phys.414(2013)45.

[39]S.L.Hu,Z.X.Zhao,and T.Y.Shi,Chin.Phys.Lett.30(2013)103103.

[40]D.A.Telnov and Shih-I.Chu,Phys.Rev.A 79(2009)041401(R).

[41]X.Chu,Phys.Rev.A 82(2010)023407.

[42]X.Chu and M.McIntyre,Phys.Rev.A 83(2011)013409.

[43]T.Otobe and K.Yabana,Phys.Rev.A 75(2007)062507.

[44]B.Zhang,J.Yuan,and Z.X.Zhao,Phys.Rev.Lett.111(2013)163001.

[45]Z.X.Zhao,X.M.Tong,and C.D.Lin,Phys.Rev.A 67(2003)043404.

[46]T.K.Kjeldsen,C.Z.Bisgaard,L.B.Madsen,and H.Stapelfeldt,Phys.Rev.A 71(2005)013418.

[47]T.K.Kjeldsen and L.B.Madsen,Phys.Rev.A 71(2005)023411.

[48]S.F.Zhao,C.Jin,A.T.Le,et al.,Phys.Rev.A 81(2010)033423.

[49]S.F.Zhao,J.Xu,C.Jin,et al.,J.Phys.B 44(2011)035601.

[50]E.P.Benis,J.F.Xia,X.M.Tong,et al.,Phys.Rev.A 70(2004)025401.

[51]S.F.Zhao,L.Liu,and X.X.Zhou,Opt.Commun.313(2014)74.

[52]L.B.Madsen,O.I.Tolstikhin,and T.Morishita,Phys.Rev.A 85(2012)053404.

[53]L.B.Madsen,F.Jensen,O.I.Tolstikhin,and T.Morishita,Phys.Rev.A 87(2013)013406.

[54]L.B.Madsen,F.Jensen,O.I.Tolstikhin,and T.Morishita,Phys.Rev.A 89(2014)033412.

[55]R.Saito,O.I.Tolstikhin,L.B.Madsen,and T.Morishita,Atomic Data and Nuclear Data Tables 103-104(2015)4.

[56]S.L.Chin,Y.Liang,J.E.Decker,et al.,J.Phys.B 25(1992)L249.

[57]T.D.G.Walsh,J.E.Decker,and S.L.Chin,J.Phys.B 26(1993)L85.

[58]T.D.G.Walsh,F.Ilkov,J.E.Decker,and S.L.Chin,J.Phys.B 27(1994)3767.

[59]A.Talebpour,C.Y.Chien,and S.L.Chin,J.Phys.B 29(1996)L677.

[60]A.Talebpour,S.Larochelle,and S.L.Chin,J.Phys.B 31(1998)L49.

[61]M.J.DeWitt,E.Wells,and R.R.Jones,Phys.Rev.Lett.87(2001)153001.

[62]E.Wells,M.J.DeWitt,and R.R.Jones,Phys.Rev.A 66(2002)013409.

[63]Z.Y.Lin,X.Y.Jia,C.L.Wang,et al.,Phys.Rev.Lett.108(2012)223001.

[64]H.P.Kang,Z.Y.Lin,S.P.Xu,et al.,Phys.Rev.A 90(2014)063426.

[65]C.Guo,Phys.Rev.Lett.85(2000)2276.

[66]S.F.Zhao,C.Jin,A.T.Le,and C.D.Lin,Phys.Rev.A 82(2010)035402.

[67]J.P.Wang,S.F.Zhao,C.R.Zhang,et al.,Mol.Phys.112(2014)1102.

[68]P.R.T.Schipper,O.V.Gritsenko,S.J.A.van Gisbergen,and E.J.Baerends,J.Chem.Phys.112(2000)1344.

[69]Shih-I.Chu,J.Chem.Phys.123(2005)062207.

[70]M.Abu-samha and L.B.Madsen,Phys.Rev.A 81(2010)033416.

[71]A.M.Perelomov,V.S.Popov,and M.V.Terent’ev,Sov.Phys.JETP 23(1966)924.

[72]F.A.Ilkov,J.E.Decker,and S.L.Chin,J.Phys.B 25(1992)4005.

[73]Y.Z.Fu,S.F.Zhao,and X.X.Zhou,Chin.Phys.B 21(2012)113101.

[74]A.T.Le,R.R.Lucchese,S.Tonzani,et al.,Phys.Rev.A 80(2009)013401.

[75]M.J.Frisch,G.W.Trucks,H.B.Schlegel,et al.,GAUSSIAN 03,Revision B.04(Gaussian Inc.Pittsburgh,PA,2003).

[76]B.M.Smirnov and A.S.Yatsenko,Phys.Usp.39(1996)211.

[77]M.Awasthi,Y.V.Vanne,A.Saenz,et al.,Phys.Rev.A 77(2008)063403.