Electronic Structure of Helium Atom in a Quantum Dot∗

Jayanta K.Saha,S.Bhattacharyya,and T.K.Mukherjee

1Indian Association for the Cultivation of Science,Jadavpur,Kolkata 700032,India

2Aliah University,IIA/27,New Town,Kolkata 700156,India

3Acharyya Prafulla Chandra College,New Barrackpore,Kolkata 700131,India

4Narula Institute of Technology,Agarpara,Kolkata 700109,India

1 Introduction

The subject of atomic systems under spatial confinement is of immense interest among the researchers since the advent of quantum mechanics as the spectral characteristics of atomic systems placed under different confinements change appreciably as compared to those of free atoms.[1−2]different types of phenomenological potentials have been used by researchers to model atoms within cavities,[3]atoms under pressure,[4]impurities in quantum dots or nano crystals,[5]nanopores,[6−7]fullerenes,[8]foreign atoms in liquid helium environment[9]etc.The study of quantum dots(QD)has got considerable attention in recent times due to its fundamental importance in theoretical researches as well as in fabricating new functional devices.The QD’s(or artificial atoms),in general,contain several electrons subjected to an external confining potential and they show similar structural properties as compared to pure atoms.The structural changes of the impurity atoms inside QD’s with reference to the parameters of confining potentials provide huge physical insight about the interactions of the atoms with surroundings.Although the bound states of confined hydrogen and helium atoms have been studied extensively by several researchers,[1−2,4]very few attempts have so far been made towards the quasi bound or resonance states of one electron impurity atom in an isolated QD[10−11]and also in case of confined two electron systems.[12−14]Transformations of two-electron bound states to Feshbach and then to shape resonances depending upon a parameter of model rectangular well-type potential representing the QD have been studied by Bylicki et al.[12]Sajeev et al.[13]and Genkinet al.[14]showed that the singly excited bound states of a two-electron atom become resonance states for appropriately chosen parameters of an external attractive spherical Gaussian type con fining potential used to model the QD.

In the present work,we have considered a spherically symmetric finite oscillator(FO)potential[3,15−16]of the type,

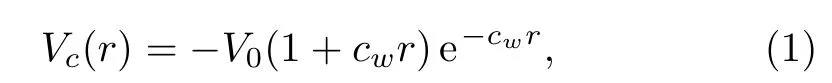
for modeling the QD con finement.Here V0is the depth of the potential well and the cavity constant cwis defined as,

where∆is the width of the potential.By tuning the parameters V0and∆,one can change the shape of the potential given by Eq.(1).Such type of two-parameter(V0and∆)potential provides much control and flexibility in modeling the size of a QD.When r→0 i.e.near the center of QD,Vc(r)∼r2and thus a harmonic nature is observed in the potential for a given cavity constant cw.But for large “r”,it deviates from the harmonic behavior.In fact,The FO potential is quite similar in profile to that of Gaussian potential.At the same time,it facilitates the computation of matrix elements in a simple and efficient manner,especially when the Slater-type orbitals are used in constructing the wave function with appropriate boundary conditions for a confined system.This FO potential was used by Winkler[15]to study the two-electron bound and resonant states of helium in QD where the electron correlation was not included initially in the optimized wave function.Even the inclusion of electron correlation could not remove the uncertainties in their calculations.[15]Later,Kimani et al.[16]applied the restricted Hartree–Fock method to estimate the ground states of many-electron close-shell quantum dots modeled by the FO potential where the electron correlations were included approximately.Chakraborty and Ho[3]made a sophisticated approach to deal with this problem by expanding the wave function in single exponent Hylleraas type basis within the framework of stabilization method,but their work was restricted to only the lowest lying doubly excited resonance state 2s2(1Se)of helium.It is worthwhile to mention that an appropriate knowledge of resonance structure of few-electron QD with and without a central impurity atom will help to understand the electron transport phenomena occurring in real semiconductor QDs.[12]

Under such circumstances,we have studied the resonance parameters of1Sestates originated from 2sns and 2pnp(n=2–5)configurations of QD confined helium below N=2 ionization threshold of He+in the framework of stabilization method[17]by using explicitly correlated multi-exponent Hylleraas type basis set.This method was successfully employed by the present workers[18−22]for calculations of resonance parameters of different resonance states of the free and confined helium-like ions.In the present study,the resonance parameters of the states under consideration are estimated over a wide range of width(∆)for a fixed depth(V0)of the FO potential.The energy values of bound 1sns(1Se)states(n=1−6)have also been reported.Moreover,the positions of 1s,2s(2S)and 2p(2P)states of He+have been estimated for a comprehensive understanding about the structure of QD confined helium.The variation of ionization potential of QD confined He with respect to the width of the FO potential has been studied.It has also been shown that the potential given by Eq.(1)breaks the orbital angular momentum(l)degeneracy in Coulomb field for the energy levels of hydrogen-like atoms.Finally,we have shown that for a fixed cavity depth(V0),the widths of the resonance states show oscillatory behavior with respect to the width(∆)of the quantum cavity.It has been noted that for higher excited states,such oscillations are more pronounced.The paper is arranged as follows:a brief discussion on the present methodology is given in Sec.2,followed by a discussion on the results in Sec.3,and finally concluding in Sec.4 with a view towards further use of the present techniques in related studies of spatially confined atomic systems e.g.QD,pressure confinement,strongly coupled plasma confinement etc.

2 Method

For any1S state of even parity arising from two electrons having same azimuthal quantum number,the variational equation[23]can be written as,

subject to the normalization condition,

where the symbols used in Eqs.(3)and(4)are same as in Ref.[23].The effective potential is given by

The multi-exponent correlated wavefunction[20]considered in the present calculation is expressed as

with

where σ’s are the non-linear parameters.Here,r1and r2are the radial co-ordinates of the electrons and r12is the relative distance between them.In a multiexponent basis set,if there are p number of non-linear parameters,then the number of terms in the radially correlated basis is p(p+1)/2 and,therefore,the dimension of the full basis(N)including angular correlation will be[(p(p+1)/2)×q],where q is the number of terms involving r12.[24]For example,as we have used here nine non-linear parameters,the number of terms in the radially correlated basis is 45 and with 10 terms involving different powers of r12,the dimension of the full basis(N)becomes 450.The values of the non-linear parameters are taken in a geometrical sequence:σi= σi−1γ,γ being the geometrical ratio.[25]The wavefunction can be squeezed or can be made more di ff use by changing the geometrical ratio(γ)keeping σ1constant throughout.To have a preliminary guess about the initial and final values of nonlinear parameter σ,we optimize the energy eigenvalues of1Sestates below N=1 ionization threshold of He+by using Nelder–Mead procedure.[26]The energy eigenroots(E)are then obtained by solving the generalized eigenvalue equation

whereis the Hamiltonian matrix,is the overlap matrix and C is a column matrix consisting of linear variational coefficients.The wavefunction is normalized for each width(∆)of the FO potential to account for the modi fi ed charge distribution inside the QD.Each energy eigenroot plotted against the geometrical ratio(γ)produces the stabilization diagram.Subsequently,we can calculate the densities of resonance states from the inverse of tangents at different points near the stabilization plateau in the neighborhood of avoided crossings for each energy eigenroot.The plots of calculated densities of resonance states versus energy for each eigenroot are then fitted separately to a standard Lorentzian pro file.The best fit,i.e.,with the least chi square(χ2)and the square of correlation(R2)near unity yields the desired position(Er)and width(Γ)of the resonance state.

For each width(∆)of the con fining potential,the energy eigenvalues of2S and2P states of confined oneelectron ion He+are obtained by using Ritz variational technique considering the wavefunction as

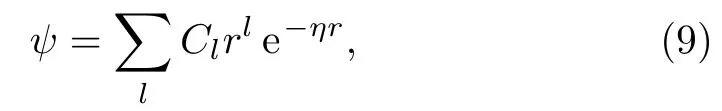
where η’s are the nonlinear parameters and C’s are the linear variational coefficients.For He+(ns)states(n=1−2),we have considered 14-parameter basis set whereas for He+(2p)state we have taken 13 parameters in the basis.In both the cases,l is ranging from 0 to 4.All calculations are carried out in quadruple precision.Atomic units have been used throughout unless otherwise specified.

3 Results and Discussions

To construct the stabilization diagram corresponding to each width(∆)of the FO potential,repeated diagonalization of the Hamiltonian matrix in the Hylleraas basis set of 450 parameters is performed in the present work for 400 different values of γ ranging from 0.63 a.u.to 0.77 a.u.A portion of the stabilization diagram for1Sestates of confined helium below N=2 ionization threshold of He+is given in Fig.1 where we have taken V0=0.2 a.u.and∆=4.0 a.u.It is evident from Fig.1 that there exist two classes of states:

(i)First few energy eigenroots lying below He+(1s)(−2.184 879 a.u.)level are insensitive with the variation of γ.This feature clearly suggests that these energy eigenroots originating from 1sns configurations of QD confined helium are bound i.e.stable against auto-ionization.

(ii)Energy eigenrootslying between He+(1s)and He+(2s)(−0.607 849 a.u.)are sensitive with the variation of γ and give rise to flat plateaus in the vicinity of avoided crossings of the energy eigenroots in the neighborhoods of some particular energy values.This is a signature of the presence of1Seresonance states of QD con fined helium.

The present calculated bound state energy eigenvalues(−E)of 1sns(1Se)(n=1–6)states of He as well as the He+(1s)energies for different cavity widths(∆)starting from a very low value of 0.001 a.u.(corresponds to almost a free case)to a high value of 1000.0 a.u.are illustrated in Fig.2.It is to be noted that for a very small cavity width∆ =0.001,the 1sns(n=1–6)energy eigenvalues of helium and the He+(1s)threshold energy inside the cavity are nearly identical to the respective energy eigenvalues of the free ions and they remain almost unaltered upto the cavity width∆=0.1 a.u.We can see from Eq.(1)that,for∆→0,cw→∞and thus,Vc→0 which produces no effect of confinement.In between∆=0.1 a.u.and 10.0 a.u.,the energy eigenvalues of helium decrease monotonically and ultimately saturate at(E1sns+2×V0)a.u.In a similar fashion,the threshold energy He+(1s)saturates at(E1s+V0)a.u.This feature is physically consistent as we can note from Eq.(1)that for∆→∞,the cavity constant cw→ 0,so that Vc(r)→ −V0.Thus the one-and two-electron energy levels undergo a downward shift by V0and 2V0respectively for∆ → ∞.The variation of the ionization potential(IP)i.e.the amount of energy required(in eV)to ionize one electron from the ground state(1s2)of helium atom is plotted against the width(∆)of the cavity in Fig.3.In accordance with the variation of energy eigenvalues of helium and its oneelectron subsystem i.e.He+,it is evident from Fig.3 that,the IP is identical with the vacuum IP for low values of∆ while,for high values of∆,it increases by an amount V0∼5.44 eV(=0.2 a.u.).It is thus evident from Figs.2 and 3 that the rates of variations of energy values of the ions are significant when the size of the confining cavity is of the order of atomic dimensions.It is thus remarkable that the stability of an impurity atom can be controlled by suitably tuning the size of a QD i.e.the depth and width of the representing cavity.

Fig.1 Stabilization diagram for1Sestates of helium atom under quantum cavity.Width of the cavity is set at 4.0 a.u.

Fig.2 The variation of bound state energy eigenvalues with reference to the width of the cavity.

Fig.3 The variation of IP with reference to the width of the cavity.

An enlarged view of the stabilization diagram(given in Fig.1)for1Sestates of He within the energy range−0.8 a.u.to−0.64 a.u.is given in Fig.4.The1Sestates of He below N=2 ionization threshold of He+(2s)can arise due to 2sns and 2pn′p(n,n′≥ 2)configurations.From a closer look at Fig.4,we can see that for a short range of γ,each eigenroot between N=1 and N=2 ionization thresholds of He+becomes almost flat in the vicinity of avoided crossings in the neighborhood of different energies.In order to calculate the exact resonance parameters,the density of states(DOS)ρ(E)is calculated by evaluating the inverse of the slope at a number of points near these flat plateaus of each energy eigenroot using the formula[18]given by:

The estimated DOS ρn(E)is then fitted to the following Lorentzian form[18]

where y0is the baseline background,A is the total area under the curve from the baseline,Eris the position of the center of the peak of the curve and Γ represents the full width of the peak of the curve at half maxima.Among different fitting curves for each eigenroot corresponding to a particular resonance state,the best fitted curve i.e.the curve with least χ2and the square of correlation(R2)closer to unity[18]yields the desired resonance energy(Er)and width(Γ).For example,the calculated DOS and the corresponding fitted Lorentzian for the 2s2(1Se)resonance state of He below He+(1s)threshold for cavity width∆=4.0 a.u.(given in Fig.5)yields resonance position Erat−0.98163 a.u.and width Γ =6.9961×10−3a.u.The evaluation of DOS following this fitting procedure has been repeated for each width of the confining potential(∆).

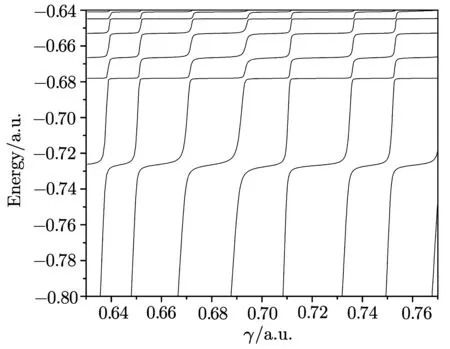
Fig.4 Enlarged view of the stabilization diagram for 1Sestates of helium atom under quantum cavity in the energy range between−8.0 a.u.to−0.64 a.u.Width of the cavity is set at 4.0 a.u.

Fig.5 Density of states and fitted lorentzian for cavity width 4.0 a.u.

Fig.6 The variation of resonance energies(Er)of 2sns(n=2–5)(1Se)states and corresponding 2s and 2p threshold energies with the cavity width(∆).

The estimated resonance energies of doubly excited 2sns(1Se)states(n=2–5)of helium and corresponding 2s and 2p threshold energies for the cavity depth V0=0.2 a.u.and cavity width(∆)ranging from 0.001 a.u.to 1000 a.u.are given in figure 6,while the variations of resonance energies(Er)of 2pnp(n=2–5)(1Se)states and corresponding 2s and 2p threshold energies versus∆are given in Fig.7.We have noted the following points.

(i)It is clear from Figs.6 and 7 that for∆=0.001 a.u.,the He+(2s)and He+(2p)states are degenerate and coincide with the energy value of N=2 ionization threshold of free He+ion.As∆increases,the He+(2s)and He+(2p)states become non-degenerate.Initially,the 2s level of He+lies energetically below the 2p level for∆up to 0.5 a.u.At∆=1.0 a.u.,the 2s state moves above the 2p level.These results exhibit that an “incidental degeneracy”takes place for 2s and 2p states of He+at some value of∆between 0.5 a.u.and 1.0 a.u.and then a “level crossing” occurs between these two states having different symmetry properties.Finally,these states become degenerate again for∆≥100.0 a.u.The incidental degeneracy for He+(2s)and He+(2p)states occur for∆in the range 0.5≤∆≤1.0.Such incidental degeneracy and subsequent level crossing phenomenon have been noted earlier by Sen et al.[27]in case of cage confined hydrogen atom and by Bhattacharyya et al.[28]in case of helium-like ions within strongly coupled plasma environment.

Fig.7 The variation of resonance energies(Er)of 2pnp(n=2−5)(1Se)states and corresponding 2s and 2p threshold energies with the cavity width(∆).

(ii)It is seen from both Figs.6 and 7 that all the resonance energies(Er)are almost unaltered up to∆=0.5 a.u.,then decrease rapidly up to∆=20.0 a.u.,and ultimately saturate.For low values of∆(say 0.001 a.u.) the resonance energies are identical with those of the free He atom whereas for∆=1000.0 a.u.the resonance energies are equal to those of free He atom plus 0.4 a.u.(i.e.2.0×V0).Thus,for a given depth(V0)of the finite oscillator potential,the variations of energies of the bound states and the resonance states of helium with reference to the width of the cavity(∆)are nearly identical.

The variation of widths(Γ)of 2sns and 2pnp(1Se)(n=2–5)resonance states with reference to ∆ are given in Figs.8 and 9 respectively.A closer look at Figs.8 and 9 leads us to the following observations.

(i)In general,it can be argued that the variation of widths shows an oscillatory behavior which are more pronounced for the higher excited states.It is worthwhile to mention here that recently Chakraborty and Ho[3]also reported such oscillation of resonance width(Γ)for 2s2(1S)state of QD confined helium atom.This feature clearly indicates a possibility of controlling the autoionization lifetimes of doubly excited states of two-electron ions by tuning the parameters of the confining FO potential representing the quantum dot.

Fig.8 The variation of resonance width(Γ)of 2sns(n=2–5)(1Se)states with the cavity width(∆).

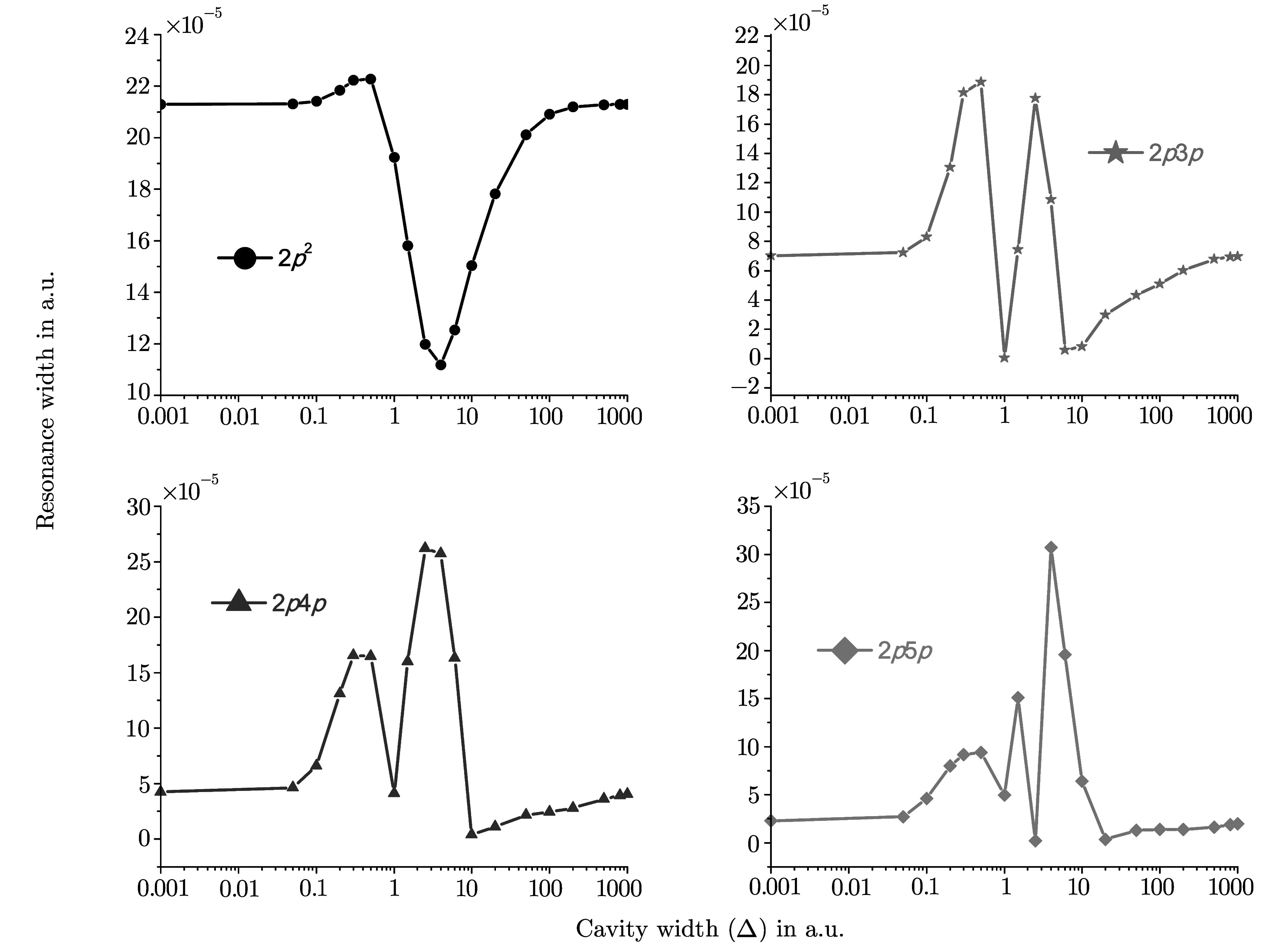
Fig.9 The variation of resonance width(Γ)of 2pnp(n=2–5)(1Se)states with the cavity width(∆).

(ii)The variations of widths of 2s2and 2p2(1Se)states with respect to∆are exactly opposite in nature.For1Sestate originating from 2s2configuration,the autoionization width first decreases within the range 0.1≤∆≤1.0 and after reaching the minima,it shows a large bump around∆≃6.0 a.u.After that it starts to decrease and fi nally the autoionization width saturates where it becomes equal to that of a free He atom.In contrast,for 2p2state,the autoionization width first increases for 0.1≤∆≤1.0 and then shows a large dip approximately at the same value of∆for which the 2s2state shows the bump.

(iii)The values of∆corresponding to the largest bump in the values of autoionization widths(Γ)of 2sns states and the lowest dip for 2pnp states shift towards the higher values of the cavity width(∆)for higher excited states.

Inside the QD i.e.due to the presence of the surrounding FO potential,the charge distribution of the impurity ion gets reoriented,which produces the behavioral changes as compared to a free ion.The nodes or antinodes of the resonance wavefunction lie at the boundary of the QD cavity and the interference caused inside the cavity gives rise to the oscillatory behavior of the resonance widths.[3,29]The number of nodes or antinodes of the wavefunction increases for high-lying resonance states and the oscillation becomes more prominent.

4 Conclusion

Structural properties of He atom confined in a QD,efficiently modeled by a two-parameter weakly confining FO type potential,have been investigated in the framework of stabilization method using explicitly correlated Hylleraastype basis sets.It has been observed that the structure of the impurity ion is a sensitive function of the dot size.For very small values of the cavity width,the system behaves almost like a free ion whereas,for very high cavity widths,a constant shift equals to the depth of the potential are observed in the energy values of the bound as well as the resonance states.When the dot size becomes comparable to the dimensions of the impurity atom,the effects are more pronounced and many remarkable behaviors such as increase in ionization potential,oscillations in the widths of two-electron resonance states,incidental degeneracy and subsequent level-crossing phenomena for one-electron ions are observed.The present work is expected to lead to future investigations on the autoionizing states of different angular momenta for QD confined two-electron systems.

References

[1]W.Jaskolski,Phys.Rep.1(1996)271.

[2]J.Sabin,E.Brandas,and S.A.Cruz,Adv.Quantum Chem.57(2009)1334;58(2009)1297.

[3]S.Chakraborty and Y.K.Ho,Phys.Rev.A 84(2011)032515.

[4]S.Bhattacharyya,J.K.Saha,P.K.Mukherjee,and T.K.Mukherjee,Phys.Scr.87(2013)065305 and references therein.

[5]D.J.Norris,A.L.Efros,and S.C.Erwin,Science 319(2008)1776.

[6]N.L.Rosi,J.Eckert,M.Eddaoudi,et al.,Science 300(2003)1127.

[7]J.L.C.Rowsell,E.C.Spencer,J.Eckert,J.A.K.Howard,and O.M.Yaghi,Science 309(2005)1350.

[8]J.A.Ludlow,T.G.Lee,and M.S.Pindzola,J.Phys.B 43(2010)235202.

[9]Solvation Effects on Molecules and Biomolecules,Computational Methods and Applications,ed.S.Canuto,Springer,Berlin(2008).

[10]S.Sahoo,Y.C.Lin,and Y.K.Ho,Physica E 40(2008)3107.

[11]S.Sahoo and Y.K.Ho,Phys.Rev.B 69(2004)165323.

[12]M.Bylicki,W.Jasklski,A.Stachw,and J.Diaz,Phys.Rev.B 72(2005)075434.

[13]Y.Sajeev and N.Moiseyev,Phys.Rev.B 78(2008)075316.

[14]M.Genkin and E.Lindroth,Phys.Rev.B 81(2010)125315.

[15]P.Winkler,Int.J.Quant.Chem.100(2004)1122.

[16]P.Kimani,P.Jones,and P.Winkler,Int.J.Quant.Chem.108(2008)2763.

[17]V.A.Mandelshtam,T.R.Ravuri,and H.S.Taylor,Phys.Rev.Lett.70(1993)1932.

[18]J.K.Saha and T.K.Mukherjee,Phys.Rev.A 80(2009)022513

[19]J.K.Saha,S.Bhattacharyya,and T.K.Mukherjee,J.Chem.Phys.132(2010)134107.

[20]J.K.Saha,S.Bhattacharyya,T.K.Mukherjee,and P.K.Mukherjee,Int.J.Quant.Chem.111(2011)1819.

[21]J.K.Saha,S.Bhattacharyya,and T.K.Mukherjee,Int.Rev.At.Mol.Phys.3(2012)1.

[22]S.Kasthurirangan,et al.,Phys.Rev.Lett.111(2013)243201.

[23]T.K.Mukherjee and P.K.Mukherjee,Phys.Rev.A 50(1994)850.

[24]J.K.Saha,S.Bhattacharyya,T.K.Mukherjee,and P.K.Mukherjee,J.Phys.B 42(2009)245701.

[25]M.Bylicki,J.Phys.B 30(1997)189.

[26]J.A.Nelder and R.Mead,Comput.J.7(1965)308.

[27]K.D.Sen,J.Chem.Phys.122(2005)194324.

[28]S.Bhattacharyya,J.K.Saha,and T.K.Mukherjee,Phys.Rev.A 91(2015)042515.

[29]L.G.Jiao and Y.K.Ho,Electronic Structure of Quantum Confined Atoms and Molecules,ed.K.D.Sen,Springer,Switzerland(2014)p.145.