On Generating Discrete Integrable Systems via Lie Algebras and Commutator Equations∗

Yu-Feng Zhang(张玉峰)and Honwah Tam

1College of Sciences,China University of Mining and Technology,Xuzhou 221116,China

2Department of Computer Science,Hong Kong Baptist University,Hong Kong,China

1 Introduction

In recent years,search for discrete integrable systems and their solutions,symmetries,Hamiltonian structures,B¨acklund transformations,conservation laws,and so on,has made rapidly developed.[1−16]A common approach for generating discrete integrable systems usually starts from the following discrete spectral problem

where ψ = (ψ1,...,ψN)Tis an N-vector and U =U(u,t,λ)is an N × N matrix which is dependent of a field vector u=(u1,...,up)T,the time variable t and a spectral parameter λ,and Ef(n,t)=f(n+1,t).To generate differential-difference integrable systems,a t-evolution part corresponding to Eq.(1)is introduced for some matrix V as follows

The compatibility condition of Eqs.(1)and(2)gives rise to a differential-difference equation

which is called a discrete zero-curvature equation. In terms of the scheme called the Tu-d scheme,[3]we should need to introduce a modified term∆for V if necessary,and denote by V(n)=V+∆so that the discrete zerocurvature equation

leads to novel integrable discrete hierarchies.It is easy to see that Eq.(4)is the compatibility condition of the Lax pair

Compared with the Tu scheme,[17]there is no commutator in the discrete zero-curvature equations(3)or(4).If we could construct a commutator appearing in Eq.(4),then we would follow the very familiar Tu scheme to generate discrete integrable systems,that is,we could imitate the well-known ideas of Tu scheme to investigate discrete integrable systems.An obvious difference between the Tu scheme and the Tu-d scheme reads that we could regularly construct the U and the V in the Lax pair(1)and(2)through Lie algebras.That is to say,set G to be a Lie algebra,and{e1,...,ep}is a basis of G.Assume again=G⊗C([λ,λ−1],where C[λ,λ−1]represents the set of Laurent polynomials in λ.A basis ofis denoted by{e1(n),...,ep(n),n∈Z}.An element R∈is called pseudo-regular if for ker ad R={x|x∈,[x,R]=0},Im ad R={x|∃y∈˜G,x=[y,R]},it holds that

and ker ad R is commutative.In addition,we define gradations ofto be as follows

Assume

where ui(i=1,...,p)are component potential functions of the function u=(u1,...,up)T.Denote α=deg(R),ǫi=deg(ei),i=1,...,p.If α and ǫisatisfy

then the stationary zero-curvature equation

could have local solutions for the given spectral matrix U.Thus,under introducing the modified term ∆ of(λnV)+which is denoted by V(n)=(λnV)++ ∆,the continuous zero-curvature equation

generally could give rise to integrable hierarchies of evolution equations.Therefore,Eq.(6)is a guidance clue to construct U and V in Eqs.(6)and(7)so that Eq.(7)could have differential solutions for V,and Eq.(8)could acquire integrable ideal equations.In order to make the Tu-d scheme match the Tu scheme as possible,we rewrite the Tu-d scheme according to the Tu scheme.First of all,a proper Lie algebra G and its loop algebra˜G are introduced.Second,we apply the˜G to introduce U and V in Eqs.(1)and(2).Third,we solve a stationary zerocurvature equation similar to Eq.(7):

where∆=E−1,[U,V]=UV−V U.

Taking a modi fi ed term ∆nfor(V λn)+,denoted by V(n)=(V λn)++ ∆n,the discrte zero-curvature equation

could lead to novel differential-difference equations.Actually,Eq.(10)is a rewritten formula of Eq.(4).Finally,with the help of the discrete trace identity proposed by Tu,[3]we can derive the Hamiltonian structure of Eq.(10).In what follows,we shall apply the above version to some explicit applications by introducing two various loop algebras of a Lie algebra.

2 Generating Two Discrete Integrable Hierarchies

The simplest basis of the Lie algebra A1reads

with the commutative relations as follows

It follows from Eq.(11)that

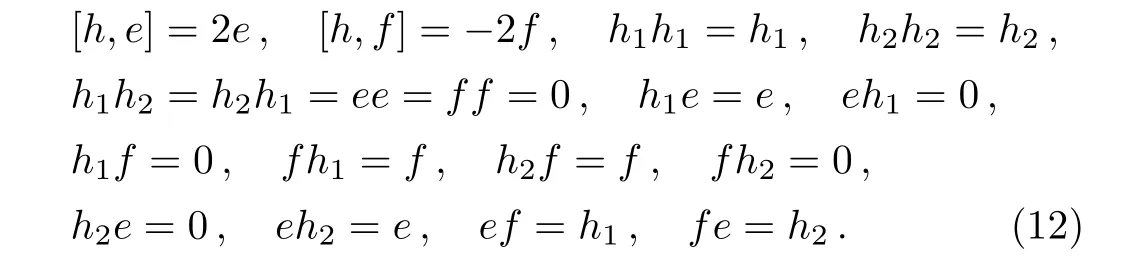
We denote by G the above Lie algebra,that is,

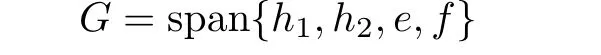
equipped with the commutative relations(11)and(12).

2.1 A Loop Algebra of the Lie Algebra G and the Toda Hierarchy

A loop algebra of the Lie algebra G is the well-known form as follows

along with degrees deghi(n)=dege(n)=degf(n)=n,i=1,2,where hi(n)=hiλn,e(n)=eλn,f(n)=fλn,i=1,2;n∈Z.We consider an isospectral problem by using˜G1

A set of solutions to Eq.(9)for V is given by

where=Eixn,x=a,b,c;i=1,2,...

Denote by

then the stationary zero-curvature equation

can be decomposed into the following form

We observe that the left-hand side of(15)contains terms with degree more than 0,while the right-hand side contains terms with degree less than 0.Hence both sides of Eq.(15)contain only terms with degree being 0.Therefore,we have

Denoting by V(m)= Γ++∆m,∆m=bm+1h1(0),a direct calculation acquires

Thus,the discrete zero-curvature equation(10)permits the lattice hierarchy

which is completely consistent with that in Ref.[3],the well-known Toda hierarchy.

Remark 1It is easy to find that the pseduo-regular element in Eq.(13)is h2(1),whose degree reads degh2(1)=1,which is more than other elements,satisfying the condition(6).In addition,Eq.(15)is similar to the decomposed equation in the Tu scheme

The above steps for computing the lattice hierarchy(16)are completely same with that by the Tu scheme,which hints that we could imitate all thoughts of Tu scheme to generate lattice hierarchies by introducing various Lie algebras and their resulting loop algebras.

2.2 Another Loop Algebra of the Lie Algebra G and a New Lattice Hierarchy

Another loop algebra of the Lie algebra G is defined as

where deghi(n)=dege(n)=degf(n)=2n+p,i=1,2;p=−1,0.An explicit loop algebra still denoted by2satisfying the above requirements is given by

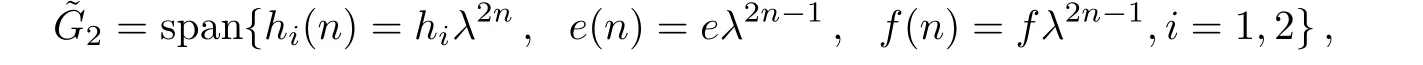
which possesses the following operating relations

from the above appearances we can derive that

Obviously,the loop algebrais different from the previous.In the following,we shall apply the loop algebrato investigate a discrete integrable hierarchy.

Set

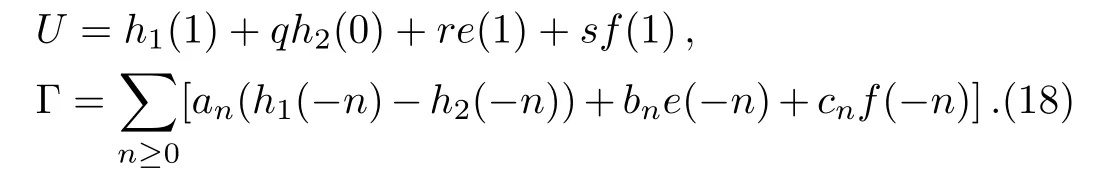
A direct calculation according to the stationary discrete equation

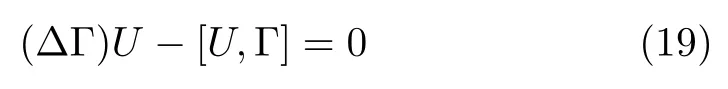
gives that

The first equation in Eq.(20)can be derived from other three ones.In fact,we have

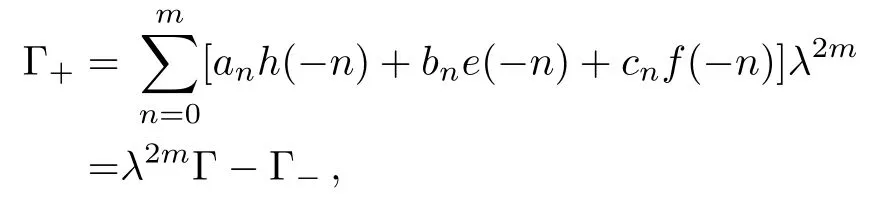
Denoting by then Eq.(19)can be decomposed into

The degrees of the left-hand side of Eq.(21)are more than−1,while the right-hand side less than 0.Therefore,both sides should be−1,0.Thus,Eq.(21)permits that

We take a modified term ∆m= δh2(0)−bme(0)−cmf(0),and denote by V(m)=Γ++∆m,it can be computed that

Therefore,Eq.(10)admits that

where δ is an arbitrary function with respect to m,t.Some reductions of Eq.(22)can be considered.

Case 1Taking q=0,δ=am,then Eq.(22)reduces to the famous Ablowtiz–Ladik hierarchy

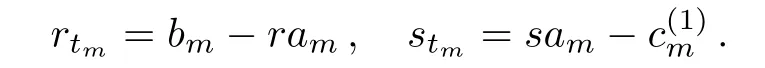
Case 2Taking δ=0,then Eq.(22)becomes

which is just the main result in Ref.[11].

Case 3Taking δ=+am,then Eq.(22)can reduce to

Again set q=0,Eq.(23)reduces to a new lattice hierarchy:

As similar to the case where the Hamiltonian structure of the Toda hierarchy(16)was derived from the discrete trace identity in Ref.[3],the Hamiltonian structures of Eqs.(22)and(23)could be investigated by the discrete trace identity,here we do not further discuss them.

3 Linear and Nonlinear Discrete Integrable Models of Toda Hierarchy

As we know that some continuous expanding integrable models of the known integrable systems,such as the AKNS system,the KN system,the KdV system,and so on,were obtained by enlarging the Lie algebra A1,e.g.see Refs.[18–20].In what follows,we want to extend the approach to the case of discrete integrable hierarchies.That is,we extend the Tu scheme for generating continuous expanding integrable models to the case by introducing commutators,as presented above,so that a great number of discrete expanding integrable systems could be readily generated just like generating expansion integrable models of continuous integrable systems.In the section,we only investigate the linear and nonlinear discrete expanding integrable models of the Toda hierarchy so that our method will be illustrated.

3.1 A Linear Discrete Integrable Coupling

Set Ref.[18]

and denote L by

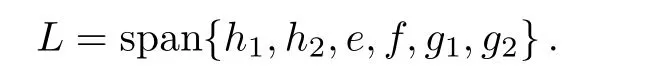
Assume L1=span{h1,h2,e,f},L2=span{g1,g2},then it is easy to see that

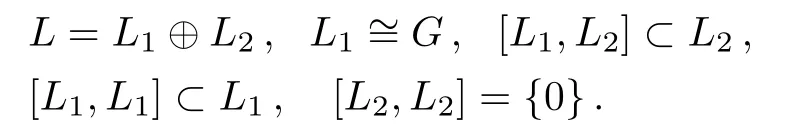
Obviously,the linear space L is an enlarging Lie algebra of the Lie algebra G presented before.Since the Lie subalgebra L1is isomorphic to the Lie algebra G,then of course have the common operation relations.Therefore,we only consider the operating relations among{g1,g2}with{h1,h2,e,f}.It is easy to compute by Maple that

A loop algebra of the Lie algebra L is defined as

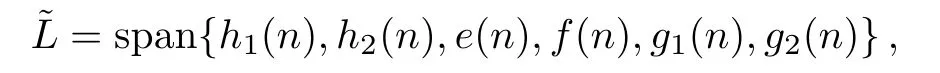
where degX(n)=n,X∈L.Applying the loop algebraintroduces the following isospectral problems

The stationary discrete zero-curvature equation(9)permits the following equatiosn by using Eqs.(11)–(12)and(24)–(26):

The first four equations in Eq.(27)are the same with Eq.(14).Set

similar to the previous discussions,we obtain that

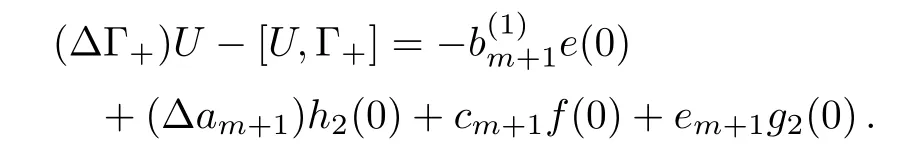
Taking V(m)= Γ++∆m,∆m=bm+1h1(0),a direct computation yields that

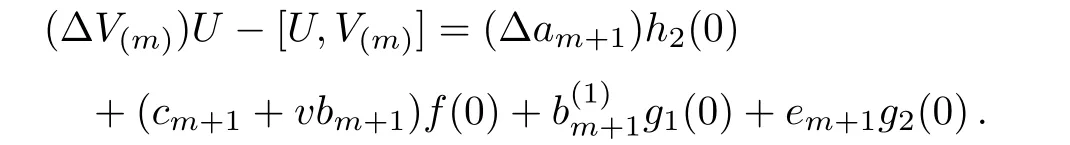
Thus,the discrete zero-curvature equation(10)permits the integrable hierarchy

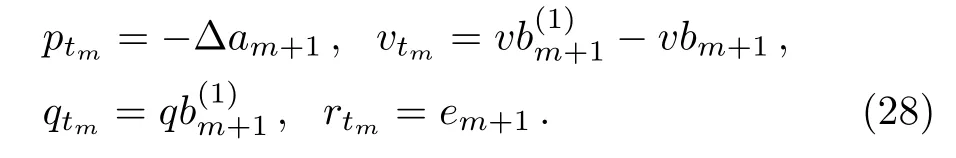
When we take q=r=0,Eq.(28)just reduces to the well-known Toda hierarchy(16).Therefore,Eq.(28)is an integrable coupling of the Toda hierarchy,of course,also a discrete integrable expanding model of the Toda hierarchy.In what follows,we deduce a discrete integrable coupling of the Toda equation.For the sake,we take

According to Eq.(27),we have

Therefore,we get a discrete integrable coupling of the Toda equation as follows

It is easy to see that Eq.(29)is a linear discrete integrable coupling with respect to the new variables q and r.Therefore,Eq.(28)is known as a linear discrete integrable coupling of the Toda hierarchy.

3.2 A Nonlinear Discrete Integrable Coupling

To search for nonlinear discrete integrable coupling of the Toda hierarchy,we should enlarge the Lie algebra G to a Lie subalgebra of the Lie algebra A3.Therefore,we set

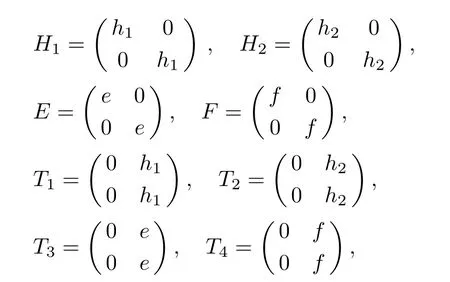
where h1,h2,e,f∈A1.We denote

here Q1=span{H1,H2,E,F},Q2=span{T1,T2,T3,T4}.If equipped with an operation for Q1as follows[X,Y]=XY−Y X,X,Y∈Q1,then Q1is a Lie algebra which is isomorphic to the previous Lie algebra G.Hence,Q1and G possess the same commutative relations.It is easy to compute by Maple that

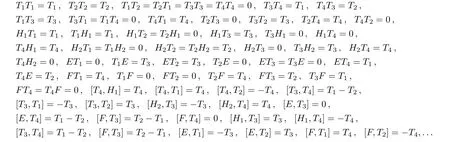
From the above computations,we find that[Q2,Q2]⊂ Q1,[Q1,Q2]⊂ Q2,which is apparently different from that of L1and L2presented before.Actually,the Lie algebra L is a Lie algebra of a homogeneous space of a Lie group,while the Q is a Lie algebra of a symmetric space of a Lie group.A corresponding loop algebra of the Lie algebra Q is defined as

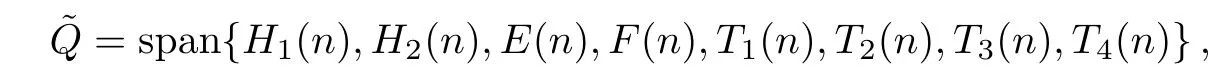
where degX(n)=n,X∈Q.In what follows,we consider the isospectral problems by using the loop algebra˜Q:

where the symbol E in the first equation of Eq.(30)stands for forward operator Ef(n)=f(n+1),which is different from the E in U and Γ in Eqs.(30)and(31).The compatibility condition of Eqs.(30)and(31)can be written as the form(10)along with a commutator operation,the corresponding stationary discrete zero-curvature equation(9)directly leads to

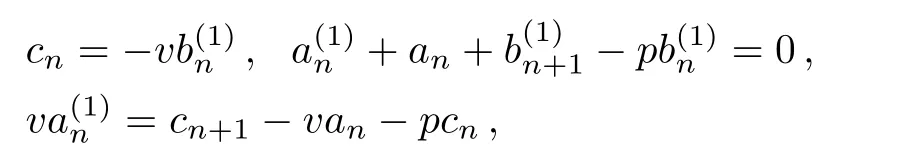
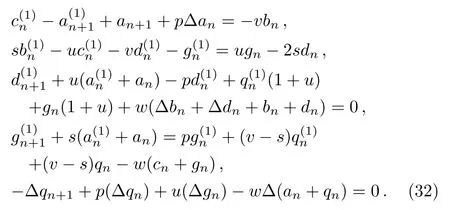
Similar to the previous discussions,we denote by

after calculations one infers that

Taking V(m)=Γ++bm+1H1(0),we can compute that

Hence,the discrete zero-curvature equation(10)admits

When u=s=w=0,Eq.(33)reduces to the Toda hierarchy.Hence,it is a discrete expanding integrable hierarchy of the Toda hierarchy,of course,a kind of discrete integrable coupling of the Toda hierarchy.In order to further recognize Eq.(33),we consider its a simple reduction when we take m=1.Given the initial values b0=c0=d0=g0=0,a0=1/2,b1=−1,c1=v,Eq.(33)reduces to

which is a set of nonlinear differential-difference equations with respect to the new variables u,s,w.Therefore,we conclude that Eq.(33)is a nonlinear discrete integrable coupling of the Toda hierarchy,which is completely different from the discrete integrable coupling(28).

Remark 2With the help of EQs.(9)and(10),generating discrete integrable hierarchies seems more complicated than the Tu-d scheme.However,we find that when the spectral matrices U and V in(1)and(2)are higher degrees,it is more convenient to deduce discrete integrable systems than the Tu-d scheme with the aid of software Maple.In addition,we do not again discuss the Hamiltonian structure of Eq.(33)in the paper.

References

[1]M.J.Ablowitz and J.F.Ladik,J.Math.Phys.16(1975)598.

[2]I.Merola,O.Ragnisco,and G.Z.Tu,Inverse Problems 10(1994)1315.

[3]G.Z.Tu,J.Phys.A 23(1990)3903.

[4]M.Bruschi,O.Ragnisco,P.M.Sanitini,and G.Z.Tu,Physica D 40(1991)273.

[5]H.W.Zhang,G.Z.Tu,W.Oevel,and B.Fuchssteiner,J.Math.Phys.32(1991)1908.

[6]C.W.Cao,X.G.Geng,and Y.T.Wu,J.Phys.A 32(1999)8059.

[7]C.W.Cao and X.X.Xu,Commun.Theor.Phys.58(2012)469.

[8]C.W.Cao and X.Yang,J.Phys.A 41(2008)025203(19pp).

[9]X.G.Geng,H.H.Dai,and J.Y.Zhu,Stud.Appl.Math.118(2007)281.

[10]X.G.Geng,J.Math.Phys.44(2003)4573.

[11]E.G.Fan and Z.H.Yang,Int.J.Theor.Phys.48(2009)1.

[12]Z.N.Zhu and H.W.Tam,J.Phys.A 37(2004)3175.

[13]D.J.Zhang and D.Y.Chen,J.Phys.A 35(2002)7225.

[14]Y.B.Suris,J.Phys.A 30(1997)2235.

[15]W.X.Ma and B.Fuchsteiner,J.Math.Phys.40(1999)2400.

[16]Z.J.Qiao,Chin.Sci.Bull.44(1999)114.

[17]G.Z.Tu,J.Math.Phys.30(1989)330.

[18]Y.F.Zhang and H.Q.Zhang,J.Math.Phys.43(2002)466.

[19]W.X.Ma and M.Chen,J.Phys.A 39(2006)10787.

[20]W.X.Ma,J.H.Meng,and H.Q.Zhang,Global J.Math.Sciences 1(2012)1.