A Note on the Equivalence of Post-Newtonian Lagrangian and Hamiltonian Formulations∗

Rong-Chao Chen(陈荣超)and Xin Wu(伍)

Department of Physics and Institute of Astronomy,Nanchang University,Nanchang 330031,China

1 Introduction

In classical mechanics,Lagrangian and Hamiltonian formulations are completely the same description of a dynamical system.Usually more attention to the Hamiltonian formulation is paid because it has properties of a canonical system.

In post-Newtonian(PN)mechanics of general relativity,the two formulations are still adopted.Are they completely equivalent?Ten years ago two independent groups[1−2]answered this question. They proved the complete physical equivalence of the third-order post-Newtonian(3PN)Arnowitt–Deser–Misner(ADM)coordinate Hamiltonian approach to and the 3PN harmonic coordinate Lagrangian approach to the dynamics of spinless compact binaries.This result was recently extended to the inclusion of the next-to-next-to-leading order(4PN)spin-spin coupling.[3]

However,there are two different claims on the chaotic behavior of compact binaries with one body spinning and spin effects restricted to the leading-order spin-orbit(1.5PN)coupling.That is to say,the 2PN harmonic coordinate Lagrangian dynamics allow the onset of chaos,[4]but the corresponding 2PN ADM Hamiltonian dynamics are integrable,regular and non-chaotic.[5−6]

An explanation to the opposite results was given in Ref.[7].In fact,the 2PN Hamiltonian and Lagrangian formulations are not exactly equal but are only approximately related.The equations of motion from the Lagrangian formulation use lower-order terms as approximations to higher-order acceleration terms in the Euler-Lagrange equations,while these approximations do not occur in the equations of motion from the Hamiltonian formulation.Naturally,the Lagrangian has approximate constants of motion but the Hamiltonian contains exact ones.These facts were regarded as the essential point for the two formulations having different dynamics.In this sense,the two claims that seem to be explicitly conflicting were thought to be correct.

Recently,the authors of Ref.[8]revisited the equivalence between the Hamiltonian and Lagrangian formulations at PN approximations.They pointed out that the two formulations at the same PN order are nonequivalent in general and have differences.Three simple examples of PN Lagrangian formulations were used to show that the differences are not mainly due to the Lagrangian having the approximate Euler-Lagrange equations and the approximate constants of motion but come from truncation of higher-order PN terms between the two formulations transformed.These examples include a relativistic restricted three-body problem with the 1PN contribution from the circular motion of two primary objects,a spinning compact binary system with the Newtonian term and the leading-order spin-orbit coupling,[8]and a binary system of the Newtonian term and the leading-order spinorbit and spin-spin couplings.[9]As an important result of Ref.[8],an equivalent Hamiltonian of a lower-order Lagrangian is usually at an in finite order from a theoretical point of view or at a high enough order from numerical computations.In terms of this point,the integrability or non-integrability of the Lagrangian can be known with the help of that of the Hamiltonian.More recently,chaos in comparable mass compact binary systems with one body spinning was completely ruled out.[10]This is because a completely canonical higher-order Hamiltonian equivalent to a lower-order conservative Lagrangian holds four integrals of the total energy and the total angular momentum in an eight-dimensional phase space,and then is typically integrable.[11]This result is helpful to clarify the doubt on the absence of chaos in the 2PN ADM Hamiltonian approach[5−6]and the presence of chaos in the 2PN harmonic coordinate Lagrangian formulation for the case of one body spinning.[4]As a point to illustrate,two other doubts about different chaotic indicators resulting in different dynamical behaviours of spinning compact binaries among Refs.[12–15]and different descriptions of chaotic parameter spaces and chaotic regions between two articles[4,16]have been clarified in Refs.[17–19].

It is worth noting that the result of Ref.[8]on the equivalence of the PN Hamiltonian and Lagrangian approaches at different orders is not easy to check in most cases because the exactly equivalent Hamiltonian of the Lagrangian is generally expressed as an in finite series whose convergence is unknown clearly.To provide enough evidence for supporting this result,we select a part of the 1PN Lagrangian formulation of relativistic circular restricted three-body problem,[20]in which the Euler-Lagrange equations can be described by a converged Taylor series and the equivalent Hamiltonian can also be written as another converged Taylor series.For our purpose,the Hamiltonian is derived from the Lagrangian in Sec.2.Then in Sec.3 numerical methods are used to evaluate whether various PN order Hamiltonians and the 1PN Lagrangian with various PN order Euler-Lagrange equations are equivalent.Finally,the main results are concluded in Sec.4.

2 Post-Newtonian Approximations

As in classical mechanics,a Lagrangian formulation L,r)and its Hamiltonian formulation H(p,r)satisfy the Legendre transformation in PN mechanics. This transformation is written as

Here r andare coordinate and velocity,respectively.Canonical momentum is given by

Taking a special PN circular restricted three-body problem as an example,now we derive the Hamiltonian from the Lagrangian in detail.

2.1 Lagrangian Formulation

The circular restricted three-body problem means the motion of a third body(i.e.a small particle of negligible mass)moving around two masses m1and m2(m1≥m2).The two masses move in circular,coplanar orbits about their common center of mass,and have a constant separation a and the same angular velocity.They exert a gravitational force on the particle but the third body does not affect the motion of the two massive bodies.Taking the unit of mass G(m1+m2)=1,we have the two massesµ1=m1/(m1+m2)and µ2=m2/(m1+m2).The unit of length requires that the constant separation of the two bodies should be unity.The common mean motion(i.e.the Newtonian angular velocity ω0)of the two primaries is also unity.In these unit systems,the two bodies are stationary at points O1(x1,0)and O2(x2,0)with x1= −µ2and x2=µ1in the rotating reference frame.The state variables(,r)of the third body satisfy the following Lagrangian formulation

In the above equations,the related notations are specified as follows.U is of the form

where the distances from body 3 to bodies 1 and 2 are

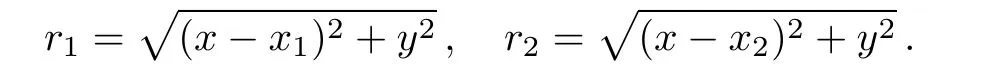
L0stands for the Newtonian circular restricted three-body problem.L1is an indirect 1PN contribution due to the relativistic effect to the circular motions of the two primaries,which results in the relativistic effect to the third body.L2is a direct 1PN contribution from the relativistic effect to the third body,and is only a part of that in Ref.[20]for our purpose.ω1is the 1PN effect with respect to the angular velocity ω0of the primaries and is expressed as

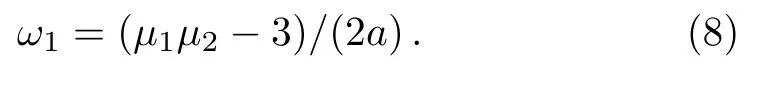
In fact,the separation a plays an important role in a mark of the 1PN effects on L1and L2when the velocity of light,c,is taken as one geometric unit in later numerical computations.

The Lagrangian(3)is a function of velocities and coordinates,therefore,its equations of motion are the ordinary Euler-Lagrange equations:

Since the momenta px=∂L/∂and py=∂L/∂in Eq.(2)satisfying the relations

are linear functions of velocitiesand,accelerations can be solved exactly from Eq.(9).Their detailed expressions are of the forms The Newtonian terms X0and Y0and the 1PN terms X1and Y1are

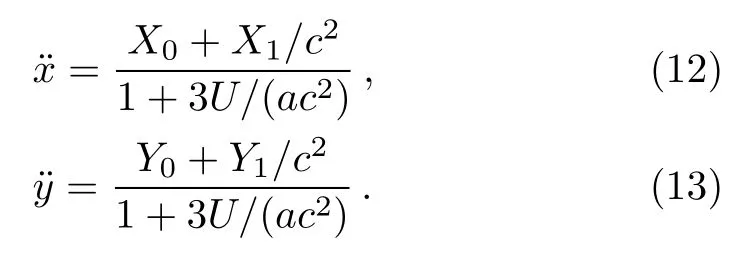
where Ux= ∂U/∂x and Uy= ∂U/∂y.Considering that δ=3U/a is at the 1PN level,Eqs.(12)and(13)have the Taylor expansions

They are the Euler-Lagrange equations with PN approximations to an order k≥1,labeled as ELk.Note that the case of k=0 with X1=Y1=0 corresponds to the Newtonian Euler-Lagrange equations,marked as EL0.From a theoretical viewpoint,as k→∞,ELkis strictly equivalent to EL given by Eqs.(12)and(13),namely,EL∞≡ EL.However,the momenta in the generic case of Ref.[8]are highly nonlinear functions of velocities,so no exact equations of motion similar to Eqs.(12)and(13)but approximate equations of motion can be obtained from the Euler-Lagrange equations(9).This shows that we do not know what the PN approximations like Eqs.(18)and(19)are converged as k→∞.

2.2 Hamiltonian Formulations

The velocities˙x and˙y obtained from Eqs.(10)and(11)are expressed as

Of course,they can be expanded to the k-th order in the forms

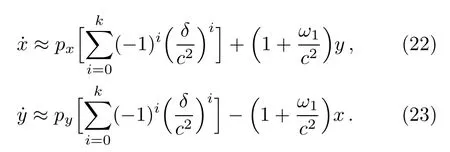
As mentioned above,Eqs.(22)and(23)are exactly identical to Eqs.(20)and(21)when k→∞.

In light of Eqs.(1),(20),and(21),we have the following Hamiltonian

Its Taylor series at the k-th order reads

It is clear that H0with ω1=0 is the Newtonian Hamiltonian formulation,and can be expressed in terms of the Jacobian constant CJas H0≡ −CJ/2.Additionally,Hkis closer and closer to H as k gets larger.Without doubt,the exact equivalence between H and Hkshould be H∞≡H.Of course,what Hkis converged as k→∞is still unknown for the general case in Ref.[8].

It should be emphasized that ELkis the k-th order PN approximation to the Euler-Lagrange equations EL that is exactly derived from the 1PN Lagrangian L,and Hkis the k-th order PN approximation to the Hamiltonian H.Because of the exact equivalence between EL and H,ELkis the k-th order PN approximation to the Hamiltonian H,and Hkis the k-th order PN approximation to the Euler-Lagrange equations EL.Additionally,EL∞and H∞are exactly equivalent,i.e.,EL∞≡EL⇔H≡H∞.However,it would be up to a certain higher enough finite order k rather than up to the in finite order k that the equivalence ELk⇔Hkcan be checked by numerical methods.See the following numerical investigations for more details.

3 Numerical Investigations

Besides the above analytical method,a numerical method is used to estimate whether these PN approaches have constants of motion and what the accuracy of the constants is. Above all,we are interested in knowing whether these PN approaches are equivalent.

3.1 Energy Errors

An eighth-and ninth-order Runge–Kutta–Fehlberg algorithm of variable time-steps is used to solve each of the above Euler-Lagrange equations ELkand Hamiltonians Hk.Parameters and initial conditions are CJ=3.12,µ2=0.001,x=y=0.55 and˙x=0.Note that the initial positive value of˙y is given by the Jacobian constant.This orbit in the Newtonian problem L0is a Kolmogorov–Arnold–Moser(KAM)torus on the Poincar´e section y=0 with˙y>0 in Fig.1(a),therefore,it is regular and nonchaotic.This integrator can give errors of the energy H0for the Lagrangian system L0in the magnitude of about an order 10−13.The long-term accumulation of energy errors is explicitly present in Fig.1(b)because the integration scheme itself yields an artificial excitation or damping.If this accumulation is neglected,the energy should be constant.This shows that the energy H0is actually an integral of the Lagrangian L0.However,the existence of this excitation or damping does not make the numerical results unreliable during the integration time of 105due to such a high numerical accuracy.Thus the integrator does not necessarily use manifold correction methods,[21−24]and gives true qualitative results,as a symplectic integration algorithm[25−28]does.

When the PN terms L1and L2are included,what about the accuracy of energy integrals given by the related PN approximations?Let us consider this question.Taking the separation between the primaries,a=31,we plot Fig.2(a)in which the errors of energies of the 1PN Euler-Lagrange equations EL1and Hamiltonian H1are shown.It is worth noting that the error of energy is estimated in terms of∆=H1−˜H1,where H1denotes the energy of EL1at time t and˜H1is the initial energy.Obviously,the energy error for EL1is larger in about 10 orders of magnitude than that for H1.This result should be very reasonable because the differences between EL1and H1exist explicitly,as shown in the above analytical discussions.The canonical equations are exactly derived from the 1PN Hamiltonian H1,therefore,the accuracy of H1is better than that of EL1.In other words,the difference between EL1and H1is at 2PN level.Of course,the higher the order k gets,the smaller the difference between ELkand Hkbecomes.This is why we can see from Figs.2(a)and 2(b)that the error of the 8PN Euler-Lagrange equations EL8and Hamiltonian H8is typically smaller than that of the 1PN Euler-Lagrange equations EL1and Hamiltonian H1.Without doubt,EL and H should be the same in the energy accuracy if no roundoff errors exist in Fig.2(c).

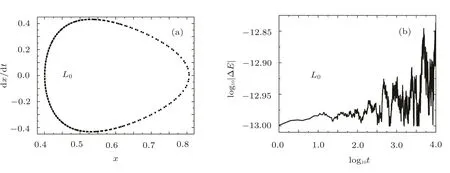
Fig.1 (a)Poincar´e section y=0(˙y>0)of an orbit with parameters CJ=3.12 andµ2=0.001 and initial conditions x=y=0.55 and˙x=0 in the Newtonian problem L0.(b)Energy error∆E=H0−˜H0,where H0and˜H0are respectively energies at times t and 0.

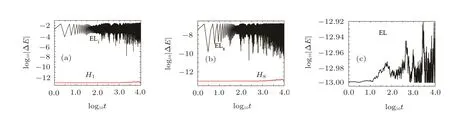
Fig.2 Energy errors∆E for the related PN Lagrangian formulations with the separation a=31.Here are some examples to illustrate notations.In∆E=H1−˜H1for EL1,˜H1is the initial energy and the energy H1at time t is obtained from the solution of EL1.For H1,∆E=H1−˜H1,where the energy H1at time t is directly given by the solution of H1.For EL,∆E=H−˜H,where˜H represents the initial energy and the energy H at time t is determined by the solution of EL.

In addition to evaluating the accuracy of energy integrals of these PN approaches,evaluating the quality of these PN approaches to the Euler-Lagrange equations EL or the Hamiltonian H is also necessary from qualitative and quantitative numerical comparisons.See the following demonstrations for more information.

3.2 Qualitative Comparisons

Besides the method of Poincar´e sections,the method of Lyapunov exponents is often used to detect chaos from order.It relates to the description of average exponential deviation of two nearby orbits.Based on the two-particle method,[29]the largest Lyapunov exponent is calculated according to the expression

where d(0)and d(t)are distances between the two nearby trajectories at times 0 and t,respectively.A globally stable orbit is said to be regular if λ =0 but chaotic if λ >0.Generally speaking,it costs a long enough time to obtain a stabilizing limit value of λ.Instead,a quicker method to find chaos is a fast Lyapunov indicator,[30−31]defined as

The globally stable orbit is chaotic if this indicator increases exponentially with time log10t but ordered if this indicator grows polynomially.

It can be seen clearly from the Poincar´e section of Fig.3(a)that the dynamics of EL or H in Fig.2(c)is chaotic.This result is supported by the Lyapunov exponents in Figs.3(b)and 3(c)and the FLIs in Figs.3(d)and 3(e).What about the dynamics of these various PN approximations?The key to this question can be found in Figs.3(b)–3(e).Here are the related details.As shown in Fig.3(b),lower order PN approximations to the Euler-Lagrange equations EL,such as the 1PN Euler-Lagrange equations EL1and the 4PN Euler-Lagrange equations EL4,are so poorer that their dynamics are regular,and are completely unlike the chaotic dynamics of EL.With increase of the PN order k,higher order PN approximations to the Euler-Lagrange equations EL become better and better.For example,the 8PN Euler-Lagrange equations EL8allows the onset of chaos,as EL does.Seen particularly from the evolution curve on the Lyapunov exponent and time,the 12PN Euler-Lagrange equations EL12seems to be very closer to EL.These results are also suitable for the PN Hamiltonian approximations to the Hamiltonian H in Fig.3(c).When the Lyapunov exponents in Figs.3(b)and 3(c)are replaced with the FLIs in Figs.3(d)and 3(e),similar results can be given.

When the separation a=138 is taken instead of a=31 in Fig.3(a),an ordered KAM torus occurs.That means that the EL dynamics is regular and non-chaotic. In Figs.3(f)–3(i),lower order PN approximations such as EL8(or H8)have chaotic behaviors,but higher order PN approximations such as EL12(or H12)have regular behaviors.

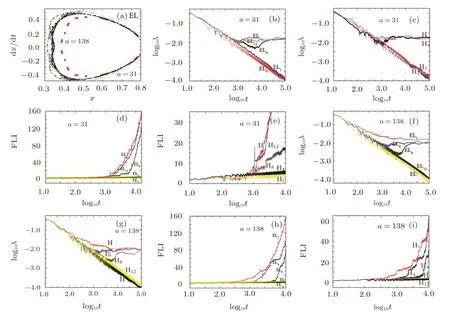
Fig.3 (a)Poincar´e section for the orbit of Fig.1 in the PN Euler-Lagrange equations EL with the separation a=31 or a=138.(b),(c),(f)and(g)relate to Lyapunov exponents λ.(d),(e),(h)and(i)deal with the fast Lyapunov indicators(FLIs).

In short,the above numerical simulations seem to tell us that the Euler-Lagrange equations(or the Hamiltonian approaches)at higher enough PN orders have the same dynamics as the Euler-Lagrange equations EL(or the Hamiltonian H).There is a question of whether these results depend on the separation a.To answer it,we resemble the authors of Ref.[32]who used the FLIs to trace a dynamical sensitivity to the variation of the parameter a.We fix the above-mentioned orbit but let a begin at 10 and end at 250 in increments of 1.For each given value of a,the FLI is obtained after integration time t=3500.In this way,we have dependence of FLIs on the separations a in several PN Lagrangian and Hamiltonian approaches.

Fig.4 Dependence of FLIs on the separation a.

Table 1 Ordered and chaotic domains of the separation a∈[10,250]in Fig.4.

As shown in Fig.4.Here 5.5 is referred as a threshold value of FLI for distinguishing between the regular and chaotic cases at this time.That is to say,an orbit is chaotic when its FLI is larger than threshold but ordered when its FLI is smaller than threshold.In light of this,we do not find that there are dramatic dynamical differences between the Euler-Lagrange equations EL(or the Hamiltonian H)and the various PN approximations(e.g.the 1PN Hamiltonian H1and the 1PN Euler-Lagrange equations EL1).However,it is clearly displayed in Table 1 that regular and chaotic domains of smaller separations a in the lowest PN approaches EL1and H1are explicitly different from those in EL or H.As claimed above,this result is of course expected.When the order k gets higher and higher,ELkand Hkhave smaller and smaller dynamical differences compared with EL or H.Two points are worth noting.First,the same order PN approaches like EL12and H12(but unlike EL and H)are incompletely equivalent in the dynamical behaviors for smaller values of a.Second,all the PN approaches EL1,H1,EL12,H12,...,EL and H can still have the same dynamics when a is larger enough.The two points are due to the differences among these approaches from the relativistic effects depending on a;smaller values of a result in larger relativistic effects but larger values of a lead to smaller relativistic effects.

3.3 Quantitative Comparisons

Now we are interested in quantitative studies on the various PN approximations ELkto the Hamiltonian H and the various PN approximations Hkto the Euler-Lagrange equations EL.In other words,we want to know how the deviation|∆r|=|rk−rH|between the position coordinate rkfor ELkand the position coordinate rHfor H varies with time.We also pay attention to the variation of|∆r|=|¯rk−rEL|between¯rkfor Hkand rELfor EL.To provide some insight into the rule on the deviation with time,we should consider the regular dynamics in the PN approximations because the chaotic case gives rise to exponentially sensitive dependence on initial conditions.For the sake of this purpose,the parameters and initial conditions unlike the aforementioned ones are CJ=2.07,x=0.68 and y=0.When a=140 is given in Fig.5(a),the curve EL is used to estimate the accuracy of numerical solutions between H and EL,which begins in the magnitude of 10−14and is in the magnitude of 10−7at time t=10000.The difference between the numerical solutions of H and EL1is rather large.With the increase of k,ELkis soon closer to H.For instance,EL8is basically consistent with H after time t=3000,and EL12is almost the same as H.Similarly,this rule is suitable for the approximations Hkto the Euler-Lagrange equations EL in Fig.5(b).After the integration time reaches 10000 for each a∈[10,10000]in Figs.5(c)and 5(d),appropriately larger separation a and higher enough order k are present such that ELkand Hkare identical to H or EL.In a word,it can be seen clearly from Fig.5 that ELkand Hkare equivalent as k is sufficiently large.

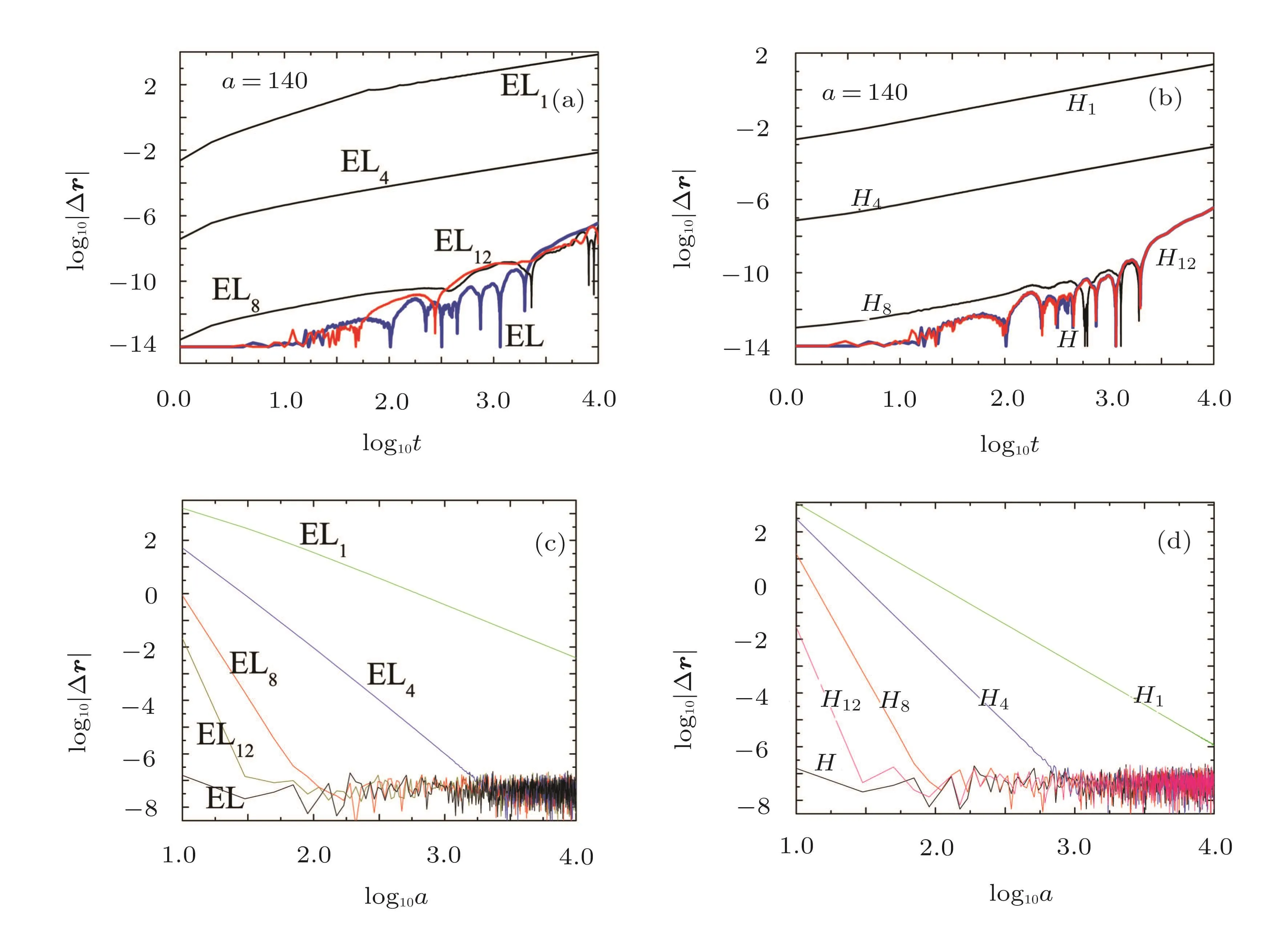
Fig.5 Deviation|∆r|between position solutions of the related PN Lagrangian and Hamiltonian formulations.(a)and(c)are the deviations from H to EL,ELi(i=1,4,8,12).(b)and(d)relate to the deviations from EL to H,Hi.

4 Summary

In general,PN Lagrangian and Hamiltonian formulations at the same order are nonequivalent due to higher order terms truncated.A lower order Lagrangian is possibly identical to a higher enough order Hamiltonian.It is difficult to check this equivalence because the Euler-Lagrange equations are not exactly but approximately derived from the Lagrangian.To cope with this difficulty,we take a simple relativistic circular restricted three-body problem as an example and investigate the equivalence of PN La-grangian and Hamiltonian formulations.This dynamical problem is described by a 1PN Lagrangian formulation,in which the Euler-Lagrange equations are exactly given and can be expressed as a converged in finite PN order Taylor series.The Lagrangian has an exactly equivalent Hamiltonian,expanded to another converged in finite PN order Taylor series.Numerical results support the equivalence of the 1PN Lagrangian with the Euler-Lagrange equations at a certain specific higher order and the PN Hamiltonian approach to a higher enough order.In this way,we support indirectly the general result of Refs.[8,10]that a lower order Lagrangian approach with the Euler-Lagrange equations at some sufficiently higher order can be equivalent to a higher enough order Hamiltonian approach.

References

[1]T.Damour,P.Jaranowski,and G.Sch¨afer,Phys.Rev.D 63(2001)044021;66(2002)029901.

[2]V.C.de Andrade,L.Blanchet,and G.Faye,Classical Quantum Gravity 18(2001)753.

[3]M.Levi and J.Steinho ff,J.Cosmol.Astropart.Phys.12(2014)003.

[4]J.Levin,Phys.Rev.D 67(2003)044013.

[5]C.Knigsdr ff er and A.Gopakumar,Phys.Rev.D 71(2005)024039.

[6]A.Gopakumar and C.K¨onigsd¨or ff er,Phys.Rev.D 72(2005)121501(R).

[7]J.Levin,Phys.Rev.D 74(2006)124027.

[8]X.Wu,L.Mei,G.Huang,and S.Liu,Phys.Rev.D 91(2015)024042.

[9]H.Wang and G.Q.Huang,Commun.Theor.Phys.64(2015)159.

[10]X.Wu and G.Huang,Mon.Not.R.Astron.Soc.452(2015)3167.

[11]X.Wu and Y.Xie,Phys.Rev.D 81(2010)084045.

[12]J.Levin,Phys.Rev.Lett.84(2000)3515.

[13]J.D.Schnittman and F.A.Rasio,Phys.Rev.Lett.87(2001)121101.

[14]N.J.Cornish and J.Levin,Phys.Rev.Lett.89(2002)179001.

[15]N.J.Cornish and J.Levin,Phys.Rev.D 68(2003)024004.

[16]M.D.Hartl and A.Buonanno,Phys.Rev.D 71(2005)024027.

[17]X.Wu and Y.Xie,Phys.Rev.D 76(2007)124004.

[18]X.Wu and Y.Xie,Phys.Rev.D 77(2008)103012.

[19]G.Huang,X.Ni,and X.Wu,Eur.Phys.J.C 74(2014)3012.

[20]G.Huang and X.Wu,Phys.Rev.D 89(2014)124034.

[21]X.Wu,T.Y.Huang,X.S.Wan,and H.Zhang,Astron.J.313(2007)2643.

[22]D.Z.Ma,X.Wu,and S.Y.Zhong,Astrophys.J.687(2008)1294.

[23]S.Y.Zhong and X.Wu,Phys.Rev.D 81(2010)104037.[24]D.Z.Ma,Z.C.Long,and Y.Zhu,Celest.Mech.Dyn.Astron.123(2015)45.

[25]S.Y.Zhong,X.Wu,S.Q.Liu,and X.F.Deng,Phys.Rev.D 82(2010)124040.

[26]L.Mei,X.Wu,and F.Liu,Eur.Phys.J.C 73(2013)2413.

[27]L.Mei,M.Ju,X.Wu,and S.Liu,Mon.Not.R.Astron.Soc.435(2013)2246.

[28]X.Ni and X.Wu,Research in Astron.Astrophys.14(2014)1329.

[29]X.Wu and T.Y.Huang,Phys.Lett.A 313(2003)77.

[30]C.Froeschl´e,E.Lega,and R.Gonczi,Celest.Mech.Dyn.Astron.67(1997)41.

[31]X.Wu,T.Y.Huang,and H.Zhang,Phys.Rev.D 74(2006)083001.

[32]X.N.Su,X.Wu,and F.Y.Liu,Astrophys.Space Sci.361(2016)32.