Inflation in Non-de Sitter Background with Coherent States

E.Yusofi, M.Mohsenzadeh, and M.R.Tanhayi

1Department of Physics,Ayatollah Amoli Branch,Islamic Azad University,Amol,Mazandaran,Iran

2Department of Physics,Qom Branch,Islamic Azad University,Qom,Iran

3Department of Physics,Islamic Azad University,Central Tehran Branch,Tehran,Iran

1 Introduction

Inflation scenario was originally proposed in the 1980’s in order to overcome some essential problems of the Big Bang theory.[1−3]This scenario could potentially predict the scale invariance of the power spectrum and also the Gaussian distribution of primordial fluctuations.Remarkably,inflation is thought to be responsible both for the large-scale homogeneity of the universe and the small fluctuations that were the seeds for the formation of the largescale structure(LSS).Actually,very rapid expansion of the quantum fluctuations causes the inflated modes to be freezed in the super-horizon region so that they became as the classical fluctuations.These classical density fluctuations∆ρ/ρ can appear in the form of observable temperature fluctuations i.e.∆T/T in the cosmic microwave background(CMB).[4−8]

The recent detections of observational cosmology such as scalar spectral index nsand the parameter of non-Gaussianity fNLof the CMB[9−10]opens new windows to the physics of very early universe.Actually,the recent CMB results from Planck satellite and data from the Wilkinson Microwave Anisotropy Probe(WMAP),[11]impose an interesting constraint on the value of scalar spectral index approximately to be ns=0.9603±0.0073 at 95%CL.[9]In Ref.[12],we considered this constraint to show that the index of Hankel function ν,as the general solution of in flaton field equation,lies in the range of 1.51≤ν≤1.53,§which it motivated us to the departure from BD mode to non-BD modes.

There has been a great deal of work focused on modifications of usual initial states and BD mode to calculate its effects on inflation,including α-vacuum,[13]general multi-mode squeezed states,[14−19]homogeneous initial states,[20]general Gaussian and non-Gaussian initial states,[21]coherent states and α-states,[22−23]excited initial inflationary states.[24]Also,in Refs.[25–26],the effect of having thermal initial state on the power spectrum has already been considered. In Refs.[27–28]a family of excited states that are indistinguishable from the BD mode at the level of two-point function or three point function has been considered.Noting that,any nonlinear effects in the expansion process or in the transformations between various stages of cosmic expansion process,will influence the final observable data.[13,29]In this paper we consider non-BD modes with non-linear part as the primary factors that could be an important source to generate scale-dependent power spectrum and non-Gaussianity.Such nontrivial modes have been used to calculate scale-dependent power spectrum with higher order of trans-Planckian corrections.[12,30]On the other hand in Refs.[31–32],it is proved that by using these non-BD modes,one receives a renormalized theory of quantum field in which the symmetry of curved space-time is preserved.The main purpose of present work is to calculate the effects of non-dS modes with non-linear part on the spectra of fluctuations by employing of coherent states which is the generalization of Ref.[22].

The rest of this paper proceed as follows:in Sec.2 we review our recent work[12]which is about non-dS modes and motivations applying of it.In the section, first we study quantum fluctuations of scalar field during inflation in non-dS space-time and next we compute the power spectrum with BD mode and non-dS modes.In the main Sec.3,by using non-dS modes,we generalize the results of Ref.[22]in coherent states by explicitly calculating onepoint and two-point functions.We also present some discussions about the primordial non-Gaussianity resulting from non-linear part of non-dS modes.Conclusions and outlook are given in the final section.

2 Quantum Fluctuations of Non-dS Modes

Let us start with the following action of minimally coupled real scalar field

where 8πG=~=1 is used.The scalar perturbations in the inflaton field are described in terms of the gauge invariant comoving curvature perturbation R which is given

by[7,12]

where Ψ is the spatial curvature perturbation. This form of scalar curvature in fact fixes the fictitious gauge modes.[7]Taking the dS flat metric and after expanding(1)to the second order one arrives to the Mukhanov action,

where the Mukhanov variable υ is defined as,υ =zR with z2=a2(2/H2),and the prime is the derivative with respect to conformal time τ and a is the scale factor.Therefore the equation of motion in Fourier space is given by,[7,20]

The quantization can indeed be done as follows

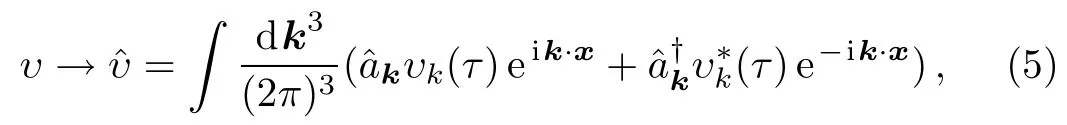
whereandare the annihilation and creation operators,respectively.Also,for the Fourier components υk,we have following decomposition,

2.1 General Non-dS Inflationary Modes

For the dynamical inflationary background,Eq.(4)changes to general form as follows,[7,12,35]

where α is given by[12,35]

The general solutions of mode equation(7)can be written as:[7,12]

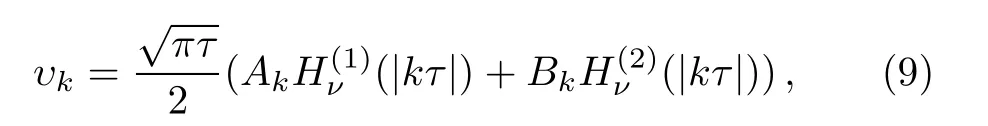
where H(1,2)νare the Hankel functions of the first and second kind,respectively.Let us consider the general form of the mode function by expanding the Hankel functions up to the higher order of 1/|kτ|

note that β = α(α − 1)/2.The positive frequency solutions of the mode equation(7)are given by[12]

These modes are non-linear in terms of both variables ν and τ.If we consider these modes up to first order of 1/kτ,we will have

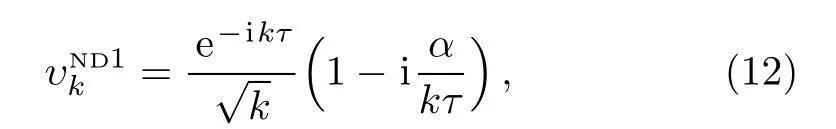
that the modes are linear in terms of τ and non-linear in terms of ν.In special case of the pure dS space-time(ν=3/2),the general form of the mode functions(11)leads to the exact BD mode:

For this case,one has a(t)=eHt,or a(τ)= −1/Hτ,with H=constant for very early universe.In Ref.[12],an asymptotically flat excited solution(11)has been considered during the inflation in which the best values of ν which are confirmed with the latest observational data,[9]is 1.51≤ν≤1.53.This result motivated us to the departure from BD mode to non-BD modes.Therefore we use non-dS modes(11)instead dS mode as the fundamental modes for our calculation in the next sections.

2.2 Scale-Dependent Power Spectrum with Non-dS Modes

As the mentioned in above,the observations of CMB and LSS tell us conclusively that the cosmic inflation is described by nearly dS space-time and the power spectrum of the fluctuations produced during inflation is nearly scale invariant(i.e.ns≈ 1).[9−10]Motivated by this fact,we use the non-dS modes instead of the usual BD mode.Using the modes introduced in Eq.(11)one obtains

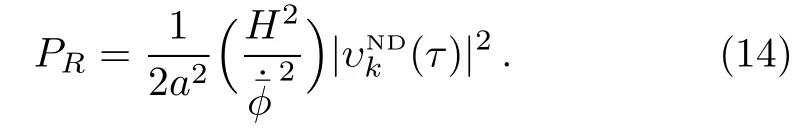
For the super-horizon limit kτ≪ 1,the following modified power spectrum in terms of ν has been calculated[12]

It is worth to mention that the following relation for τ is used,[35]

where,we have assumed that ν ≈ 3/2+ǫ with a constant slow-roll parameter ǫ.[35]This indicates that the conformal time τ can be depended on ν.On the other hand,for ND1 modes(12)one obtains the modified power spectrum as,

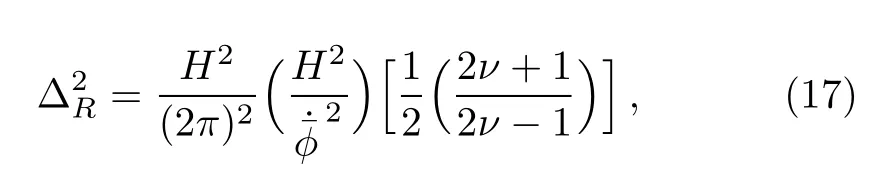
where the curvature perturbation is given by Rk(τ)=(υk(τ)/a)(H/).Also,PRandare the power spectrum and dimensionless power spectrum,[12]respectively.

For pure dS phase namely ν=3/2,one obtains

which is the same as the result of using of the BD mode and(15)reduces to the standard scale invariant power spectrum.Therefore,with regarding the above results,it is deduced the utilizing of non-dS modes,can be considered as the primary factor for generating the scaledependent power spectrum and non-Gaussian effects in CMB.Similar to our results,the non-linear corrections of power spectrum obtained from previous conventional methods.[35−44]We are going to investigate this issue by making use of coherent state in the next section.

3 Calculation of Spectra in Coherent States

Since,we do not know anything about the physical states before inflation,any excited state is as good an initial state as the vacuum state.Excited states can be made by using creation operatorsover the vacuum state|0i,

where for the excited coherent state,we have|ψi ≡ |Ci and the coherent state|Ci is defined as In fact,the coherent state is the quantum states that well describe the quantum harmonic oscillator whose dynamics resembles the classical harmonic oscillator behaviors.

If we build coherent state over the BD mode|0i in Eq.(19),the homogeneity in the large-scale as a physical constrain leads to deduce the one-point function ofin the super-horizon limit|kτ|≪ 1 to be zero,¶¶This condition only for the BD mode|0i is true,but for a general initial state and for interacting quantum field,the operatorcan have a non-vanishing expectation value.[23]

whereis defined by,

where,

So,the constrain(21)leads to the following condition

with these coherent states as the initial excited states,we can compute two-point function as follows,[22]

Note that the calculated power spectrum(25)with coherent state|Ci,is exactly like to the calculated power spectrum with BD mode|0i.Therefore one has

4 Coherent States over the Non-dS Modes

The present observations of the CMB temperature inhomogeneities indicate the presence of almost scaleinvariant spectrum of curvature perturbations.[9]On the other hand theoretically,temperature fluctuations of CMB and LSS are directly originated from the curvature perturbations produced during inflation.

The correction terms in non-dS modes were very tiny(nonzero)in the early time but can be grown in the later time.As it is known at the early time in short distance regime the energy of the universe was very high and the potential of the universe has located in the state with maximal symmetry,therefore these tiny corrections terms of initial modes at early time limit may play a role as initial sources to spontaneous symmetry bricking,bubble nucleation,and creation of inflating universe.In the context of effective field theory,in short distance scales and in the sub-horizon limit the initial symmetry may be broken by such non-linear effects to outburst and propagation quantum fields and particles[48]in the super-horizon scale to formation of large galaxies and galaxies cluster.To verify this claim,let us first build coherent excited states over non-dS modes and examine the effects of the correction terms in the sub-horizon and super-horizon limit.

It is shown in the previous section that the one-point function for coherent states built over BD mode(special case of non-dS modes with ν=3/2 and linear order of 1/kτ)in the super-horizon limit is zero under the constraint(21).In this subsection we build coherent excited states over non-dS modes and we want to compute onepoint and two-point functions,respectively.Note that all coefficients of 1/(kτ)n,n ≥ 2 in Eq.(11)are important but for simplification of calculations and results,we stop the expansion up to the second order.

4.1 Calculation of One-Point Function

We can write

where the first term on the right hand side corresponds to the linear part of non-dS modes and the second term corresponds to the contribution of non-linear part.If we apply condition(24),the first term of the above equation will be zero,however the second term is non-zero leading to

In other words the second or higher order terms of 1/kτ inserted in the non-dS modes act like general initial state or interacting field in effective field theory method.We would like to note that in the presence of three-point interaction,[45]one has hC|(τ→0)|Ci 6=0,[22−23]while in the present method,just because of the presence of higher order corrections terms of 1/kτ,we can obtain nonzero one-point function.This can lead to a non-zero three point function as the following,

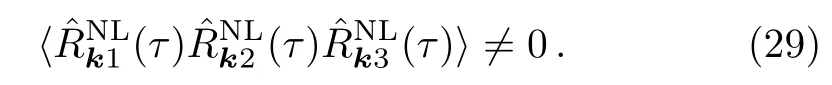
Actually,the non-dS modes can play the role of redefined fields[22−23]in the interaction picture.In the next subsections similar to the approach of Ref.[22],we will compute power spectrum with non-dS modes.

4.2 Calculation of Two-Point Function

The power spectrum is calculated as follows

with the non-dS modes of Eq.(11),one obtains

where we can write

By introducingafter making use of the non-dS modes(11),the two-point function is found to be

Equivalently,shares arising from the linear and non-linear terms of 1/kτ of non-dS modes,similar to Eq.(27),the above relation can be written as

where for the linear part of non-dS modes(11),one has

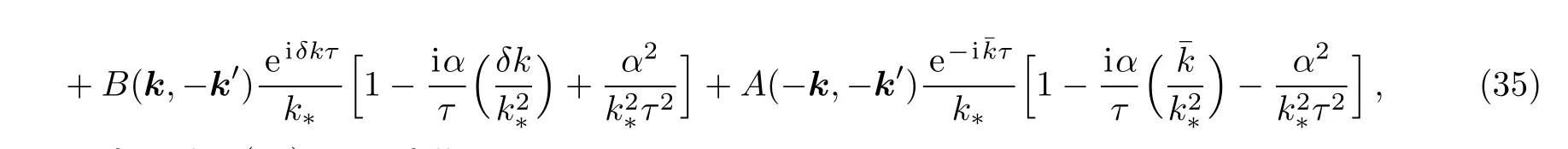
and the non-linear part of modes(11),is as follows

If we consider special case ν=3/2 or α=1,we will have β=0,andso we obtain

Noting that this result is the same as what obtained in Ref.[22]where the general initial states with BD mode have been used whereas we used the coherent states with non-dS modes.For the super-horizon limit,by applying condition(24),one achieves following constrain,

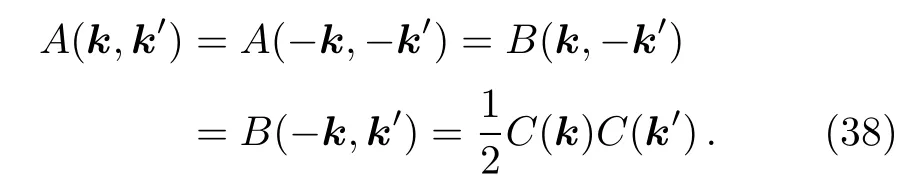
Note that by consideration above condition,the sum of the last four terms of Eq.(37)is equal to zero and we obtain

Consequently,one receives scale invariant power spectrum.Considering the general case of ν >3/2 or α 6=1,leads to β 6=0.In this case,one should consider the contribution of non-linear terms of 1/kτ in the calculation of the power spectrum.As a result,the non-zero contribution of non-linear corrections for power spectrum is obtained as,hC|ˆυk(τ)ˆυk′(τ)|CiNL6=0.Therefore,by applying condition(38)for the super-horizon limit,one obtains

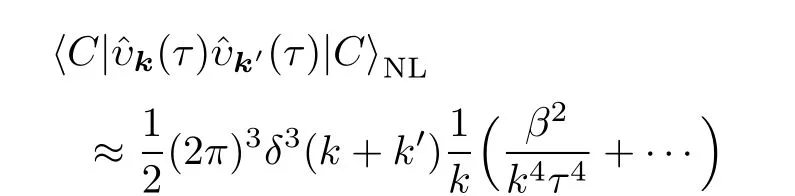
Finally,we obtain two-point function for general non-dS modes in the super-horizon limit as,

Note that,resulting from non-linear corrections terms of non-dS modes and according to the results obtained for the one-point function(28)it looks for two-point function(41)and for the three-point function(29),the corrections can be of order(≤ 1/(kτ)4)and(≤ 1/(kτ)6),respectively.For initial fixed time τ0= −MPl/Hk,if MPlis the Planck scale,H/MPlis at most 10−4,[44]and we can obtain(≤ 1/(kτ0)4) ≈ (H/MPl)4≈ 10−16and(≤ 1/(kτ0)6≈ (H/MPl)6≈ 10−24,that indicates the resulting corrections are very tiny at Planck time τ0,and it implies the nearly scale-invariant power spectrum and almost Gaussian distribution in CMB.kAn adiabatic,Gaussian and nearly scale-independent scalar power spectrum has also been confirmed by Wilkinson Microwaves Anisotropy Probe 9-year data[49]and Planck data released in 2013.[9]This final result emphasizes that our non-dS modes are more usable for far past time limit.

5 Conclusions

It is known that any deviation of Bunch–Davies initial state in inflation would lead to corrections of the power spectrum.In this paper we have employed the initial nondS modes to study the corrections of the spectra mainly coming from the comoving curvature perturbation.NondS modes are actually the asymptotic expansion of the Hankel function with index ν ≈ 3/2+ ǫ,as the general solution of in flaton field equation at very early universe.This followed from the fact that the space-time of inflation are indeed nearly dS space-time but not exact dS spacetime,this motivates one to deviate dS mode and consider general non-dS modes.As a matter of fact when one carries out the renormalization with the non-dS modes the symmetry of the space-time is preserved as long as the dS space-time is supposed to be as the background.[31]Explicitly calculations showed that using such modes leads to tiny and non-zero one-point function for far past time.This result may mean that the anisotropy of CMB radiation,can be originated from the non-linearity of the initial states.Note that the corrections obtained with non-dS modes very closely related to the non-linear corrections that have calculated with general initial states in Ref.[22],and in fact,be complementary corrections were obtained with linear BD mode.It looks the nonlinear part of non-dS modes,can play the role of redefined fields in the interaction picture to calculate of three-point functions.Finally,it is shown that the primordial non-Gaussianity in single field inflation resulting from initial non-dS states at the Planck scale,might be very tiny that con firmed by resent observation.Moreover,our results at the leading order were similar to what obtained with general initial states and in the dS limit leaded to standard result.

Although,we examine both of sub-horizon and superhorizon limits,but we emphasize that our non-trivial modes and resulting spectra are more reasonable and suitable for far past time limit,kτ≫ 1,specially for initial fixed time τ0.In future work we will study what interaction terms and what form of potential in the Lagrangian can lead to the corrections terms in the the non-dS mods.

Acknowledgments

We would like to thank Mohammad Vahid Takook,Sandipan Kundu,Hamed Pejhan for constructive conversations and comments.This work has been supported by the Islamic Azad University,Ayatollah Amoli Branch,Amol,Mazandaran,Iran.

References

[1]A.H.Guth,Phys.Rev.D 23(1981)347.

[2]A.Linde,Particles Physics and Inflationary Cosmology,Harwood Academic,Reading(1991).

[3]A.R.Liddle,An Introduction to Cosmological Inflation,(1999)[arXiv:astro-ph/9901124v1].

[4]A.A.Starobinsky,Phys.Lett.B 117(1982)175.

[5]S.W.Hawking,Phys.Lett.B 115(1982)295.

[6]A.H.Guth and S.Y.Pi,Phys.Rev.Lett.49(1982)1110.

[7]D.Baumann,TASI Lectures on Inflation,TASI(2009),[arXiv:hep-th/0907.5424].

[8]V.Mukhanov,Physical Foundations of Cosmology,December(2005).

[9]P.A.R.Ade,et al.,Planck 2013 Results.XXII.Constraints on Inflation,[arXiv:astro-ph/1303.5082];S.Unnikrishnana and V.Sahni,Resurrecting Power Law Inflation in the Light Of Planck Results,J.Cosmol.Astropart.Phys.10(2013)063,[arXiv:astro-ph/1305.5260].

[10]P.A.R.Ade,et al.,Planck 2013 Results.XXIV.Constraints on primordial non-Gaussianity,[arXiv:astroph/1303.5084].

[11]E.Komatsu,et al.,Astrophys.J.Suppl.[arXiv:astroph/0803.0547].

[12]E.Yuso fiand M.Mohsenzadeh,J.High Energy Phys.09(2014)020,[arXiv:astro-ph/1402.6968];E.Yuso fiand M.Mohsenzadeh,Modern Phys.Lett.A 30(9)(2015)1550041.

[13]W.Xue and B.Chen,Phys.Rev.D 79(2009)043518,[arXiv:hep-th/0806.4109].

[14]F.Nitti,M.Porrati,and J.W.Rombouts,Phys.Rev.D 72(2005)063503,[arXiv:hep-th/0503247].

[15]M.Porrati,Effective field theory approach to cosmological initial conditions:Self-consistency bounds and non-Gaussianities,[arXiv:hep-th/0409210].

[16]R.Holman and A.J.Tolley,J.Cosmol.Astropart.Phys.0805(2008)001,[arXiv:hep-th/0710.1302].

[17]P.D.Meerburg,J.P.van der Schaar,and P.S.Corasaniti,J.Cosmol.Astropart.Phys.0905(2009)018,[hepth/0901.4044].

[18]J.Ganc,Phys.Rev.D 84(2011)063514,[arXiv:astroph/1104.0244].

[19]I.Agullo and S.Shandera,J.Cosmol.Astropart.Phys.1209(2012)007,[arXiv:astro-ph/1204.4409].

[20]S.Bahramiand E.E.Flanagan,Primordialnon-Gaussianities in single field inflationary models with nontrivial initial states,[arXiv:astro-ph/1310.4482].

[21]N.Agarwal,R.Holman,A.J.Tolley,and J.Lin,J.High Energy Phys.1305(2013)085,[arXiv:hep-th/1212.1172];C.P.Burgess,James M.Cline,F.Lemieux,R.Holman,J.High Energy Phys.0302(2003)048,[arXiv:hepth/0210233].

[22]S.Kundu,J.Cosmol.Astropart.Phys.1202(2012)005,[arXiv:astro-ph/1110.4688].

[23]S.Kundu,Non-Gaussianity Consistency Relations,Initial States and Back-reaction,[arXiv:astro-ph/1311.1575].

[24]A.Aravind,D.Lorshbough,and S.Paban,J.High Energy Phys.07(2013)076,[arXiv:hep-th/1303.1440].

[25]K.Bhattacharya,S.Mohanty,and R.Rangarajan,Phys.Rev.Lett.96(2006)121302.[arXiv:hep-ph/0508070].

[26]P.Ferreira and J.Magueijo,Phys.Rev.D 78(2008)061301,[arXiv:astro-ph/0708.0429].

[27]A.Ashoorioon and G.Shiu,J.Cosmol.Astropart.Phys.1103(2011)025,[arXiv:1012.3392].

[28]I.Agullo and L.Parker,Phys.Rev.D 83(2011)063526,[arXiv:astro-ph/1010.5766].

[29]Y.Takamizu and T.Kobayashi,Prog.Theor.Exp.Phys.(2013)?2013(6):063E03 doi:10.1093/ptep/ptt033 First published online June 1,2013(17 pages).

[30]A.Ashoorioon,et al.,Nucl.Phys.B 727(2005)63,[arXiv:gr-qc/0504135].

[31]M.Mohsenzadeh,M.R.Tanhayi,and E.Yuso fi,Eur.Phys.J.C 74(2014)2920,DOI 10.1140/epjc/s10052-014-2920-5,[arXiv:hep-th/1306.6722].

[32]E.Yuso fiand M.Mohsenzadeh,Phys.Lett.B 735(2014)261.

[33]J.P.Gazeau,J.Renaud,and M.V.Takook,Class.Quant.Grav.17(2000)1415,[arXiv:gr-qc/9904023];H.Pejhan,M.V.Takook,and M.R.Tanhayi,Annals of Physics 341(2014),[arXiv:math-ph/1204.6001];M.Mohsenzadeh,A.Sojasi,and E.Yuso fi,Mod.Phys.Lett.A 26(2011)2697,[arXiv:gr-qc/1202.4975].

[34]T.S.Bunch and P.C.W.Davies,Proc.R.Soc.Lond.A 117(1978)360.

[35]E.D.Stewart and D.H.Lyth,Phys.Lett.B(1993)[arXiv:gr-qc/9302019].

[36]J.Martin and R.H.Brandenberger,Phys.Rev.D 63(2001)123501,[arXiv:hep-th/0005209].

[37]H.Collins and R.Holman,Phys.Rev.D 80(2009)043524,[arXiv:0905.4925];A.Ashoorioon,A.Kempf,and R.B.Mann,Phys.Rev.D 71(2005)023503,[arXiv:astroph/0410139].

[38]R.Easther,B.R.Greene,W.H.Kinney,and G.Shiu,Phys.Rev.D 64(2001)103502,[arXiv:hep-th/0104102].

[39]R.Brandenberger and P.M.Ho,Phys.Rev.D 66(2002)023517,[arXiv:hep-th/0203119].

[40]F.Lizzi,G.Mangano,G.Miele,and M.Peloso,J.High Energy Phys.0206(2002)049,[arXiv:hep-th/0203099].

[41]R.Easther,B.R.Greene,W.H.Kinney,and G.Shiu,Phys.Rev.D 66(2002)023518,[arXiv:hep-th/0204129].

[42]U.H.Danielsson,J.High Energy Phys.0207(2002)040,[arXiv:hep-th/0205227].

[43]N.Kaloper,M.Kleban,A.E.Lawrence,and S.Shenker,Phys.Rev.D 66(2002)123510,[arXiv:hep-th/0201158].[44]U.H.Danielsson,Phys.Rev.D 66(2002)023511,[hepth/0203198].

[45]N.Agarwal,R.Holman,A.J.Tolley and J.Lin,J.High Energy Phys.1305(2013)085,[arXiv:1212.1172];J.M.Maldacena,J.High Energy Phys.0305(2003)013,[arXiv:astro-ph/0210603];L.Senatore,TASI 2012 Lectures on Inflation,Published by World Scientific Publishing Co.Pte.Ltd.,Boulder,Colorado(2013).

[46]K.Goldstein and D.A.Lowe,Phys.Rev.D 67(2003)063502,[arXiv:hep-th/0208167].

[47]D.M.Regan,Measuring CMB non-Gaussianity as a probe of Inflation and Cosmic Strings,PhD Thesis,DAMTP,Cambridge(2011),[astro-ph/1112.5899].

[48]M.Mohsenzadeh,E.Yuso fi,and M.R.Tanhayi,Particle Creation with Excited de Sitter Modes,Canadian Journal of Physics 93(2015)1466,10.1139/cjp-2015-0294.

[49]G.Hinshaw,et al.,[WMAP Collaboration],Astrophys.J.Suppl.208(2013)19,[arXiv:astro-ph:1212.5226];C.Cheng and Q.Huang,Constraint on Inflation Model from BICEP2 and WMAP 9-Year Data,[arXiv:astroph/1404.1230].