时间模上二阶非线性阻尼动力方程的振动性分析

杨甲山，谭伟明，覃学文，苏 芳（梧州学院信息与电子工程学院，广西梧州543002）



时间模上二阶非线性阻尼动力方程的振动性分析

杨甲山，谭伟明，覃学文，苏 芳
（梧州学院信息与电子工程学院，广西梧州543002）

摘 要：研究了时间模T上的一类具有阻尼项的二阶非线性中立型变时滞动力方程的振动性，利用时间模上的微积分理论和大量不等式技巧，基于Riccati变换技术和H函数法，得到了该方程的5个振动定理．特别地，获得的Hille型和Kamenev型振动准则推广并改进了一些相关文献的已知结果，并给出例子说明了定理假设条件是较宽松的．

关 键 词：振动性；时间模；时滞动力方程；阻尼项；非线性中立项

振动是自然界和工程技术等领域最常见的一种现象，广泛存在于机械运动、电磁运动及原子运动等中，而振动现象往往通过方程表现出来．近年来，对微分方程及时间模上动力方程的振动性等定性理论的研究已有一些结果［1－35］．本文讨论如下时间模上的一类具有阻尼项和非线性中立项的二阶非线性变时滞中立型动力方程

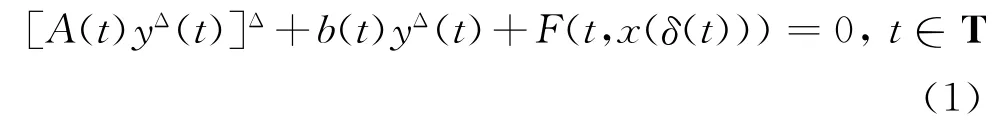
的振动性，此处y（t）＝x（t）＋B（t）g（x（τ（t））），T是任意时间模，且supT＝∞．设t0∈T且t0＞0，则［t0，∞）T为时间模区间，其定义为［t0，∞）T＝［t0，∞）∩T．方程（1）的解是指定义在时间模T上满足方程（1）的非平凡实值函数x（t），t∈T．如果方程（1）的一个解x（t）有任意大的0点，则称其为振动的，否则称x（t）是非振动的．若方程（1）的所有解都是振动的，则称其为振动的．本文只关注方程（1）的不最终恒为0的解．下文总假设：

（H1）：τ，δ：T→T都是滞量函数，τ（t）≤t，且并且τ（δ（t））＝δ（τ（t））．

（H2）：滞量τ是严格递增的＝τ（T）⊆T是一时间模，τ°σ＝σ°τ，且τΔ（t）＝τ0＞0，δ（t）≥τ（t）．

（H3）：b∈Crd（T，［0，＋∞）），即b（t）是定义在T到［0，＋∞）上的实值rd－连续函数（后面亦有类似记号，不再另作说明）；B∈Crd（T，R）且0≤B（t）≤b0＜∞（这里b0是常数）．

（H4）：A∈Crd（T，（0，＋∞）），－b／A∈R＋并且

（H5）：g∈C（R，R），且当u≠0时ug（u）＞0，g（u）／u≤η（这里0＜η≤1为常数）．

（H6）：F∈C（T×R，R），uF（t，u）＞0（u≠0），且∃P∈Crd（T，（0，∞））使得｜F（t，u）｜≥P（t）｜u｜（u≠0）．

近年来，时间模上的有关理论及时间模上动力方程的振动性的研究成果非常丰富［1－32］．最近，中立型动力方程的振动性研究也取得了很多成果［9－21，24－32］．如文献［9－10］利用时间模上的理论和广义的Riccati变换技术研究了动力方程

的振动性，得到了上述方程振动的几个判别准则，其中，中立项函数0≤p（t）＜1．文献［11－14］在同样的条件0≤p（t）＜1下研究了二阶动力方程

的振动性，得到了上述方程振动的一些充分条件，推广并且改进了一些已知结果．文献［15］利用时间模上的理论和广义的Riccati变换研究了二阶动力方程

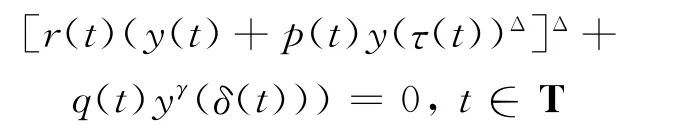
的振动性，这里仍然要求中立项函数0≤p（t）＜1．之后，其他文献如［16－21，24，26－27，30－32］都有这样的条件限制．当p（t）≥1或p（t）≤0且具有阻尼项时，却不存在方程的振荡准则．本文将基于假设（H1）～（H6），利用时间模上的理论、广义的Riccati变换技术以及大量的不等式技巧来研究方程（1）的振动性，建立了判别方程（1）振动的几个新的准则，所得结果充分反映了阻尼项和中立项在系统振动中的影响，同时改善了对中立项函数的限制条件，推广并改进了现有文献的一些结果．

1 方程的振动性结果及证明

在中立项系数函数0≤B（t）≤b0＜∞下建立振动方程（1）的充分条件前，先给出2个引理．

引理1［2］如果g∈R＋，即g（t）∈Crd（T，R），并且对于任意的t∈［t0，＋∞）T，满足1＋μ（t）g（t）＞0．则初值问题yΔ（t）＝g（t）y（t），y（t0）＝y0∈R在［t0，＋∞）T上有唯一的正解eg（t，t0），这个“指数函数”有时也记为eg（．，t0），它满足半群性质eg（a，b）eg（b，c）＝eg（a，c）．

引理2［24］若τ（t）是严格递增的T是一时间模，τ（σ（t））＝σ（τ（t））．设如果τΔ（t）和xΔ（τ（t））存在（t∈Tk），则（x（τ（t）））Δ存在，且

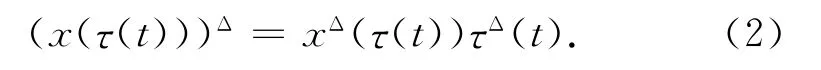
这里函数ξ（t）＝min｛P（t），P（τ（t））｝．则方程（1）在［t0，∞）T上是振动的．

证明 设方程（1）在［t0，∞）T上有一个非振动解x（t），不妨设x（t）＞0，x（τ（t））＞0，x（δ（t））＞0，t∈［t1，∞）T，t1∈［t0，∞）T（若x（t）最终为负时类似可证），则y（t）＞0．由方程（1），有

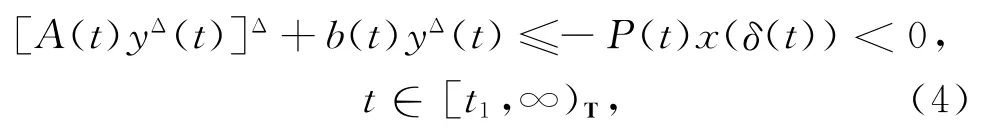
利用引理1，可得

否则∃t2∈［t1，∞）T，使得当t∈［t2，∞）T时，yΔ（t）＜0，于是，其中因此，进一步，有这与y（t）＞0矛盾，所以yΔ（t）＞0，t∈［t1，∞）T．应用式（4），可得

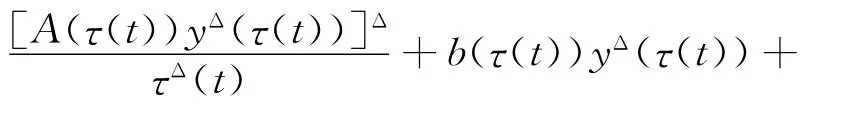
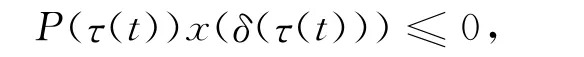
综合上式及式（4），当t∈［t1，∞）T时，得

由于y（t）≤x（t）＋b0ηx（τ（t）），并利用ξ（t）的定义及τΔ（t）＝τ0＞0，δ（t）≥τ（t），上式可写成

由式（4）知［A（t）yΔ（t）］Δ≤0，所以A（t）yΔ（t）≥A（σ（t））yΔ（σ（t）），A（τ（t））yΔ（τ（t））≥A（τ（σ（t）））yΔ（τ（σ（t））），于是，式（5）可写成

定义函数

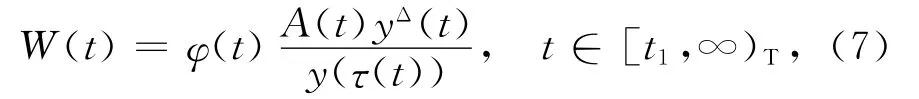
则W（t）＞0，t∈［t1，∞）T．注意到式（2），由式（7）得

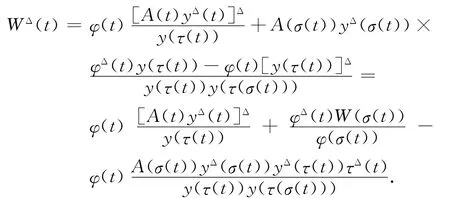
由于A（τ（t））yΔ（τ（t））≥A（σ（t））yΔ（σ（t））及y（τ（t））≤y（τ（σ（t））），因此

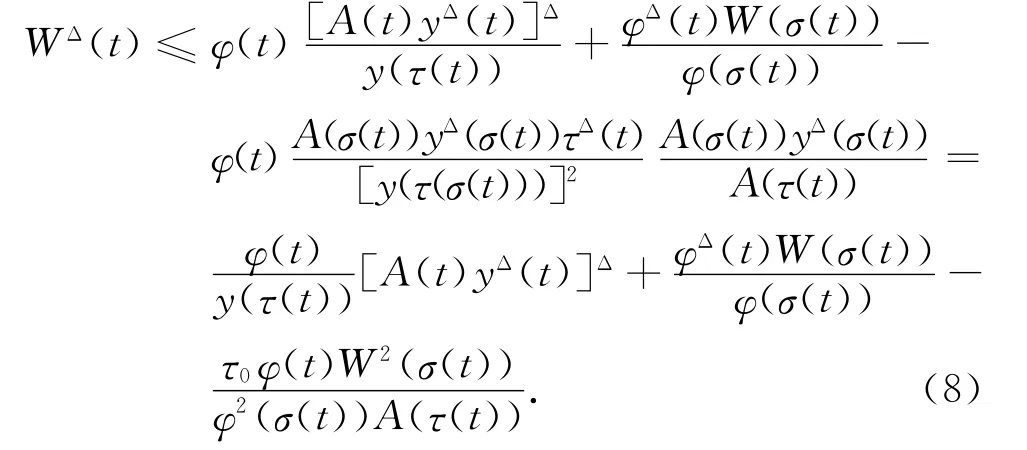
另一方面，再定义函数

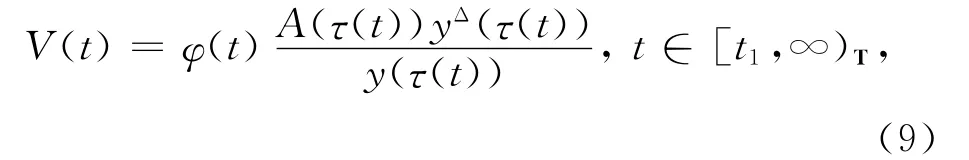
则V（t）＞0，t∈［t1，∞）T．完全类似于上面的情形，得

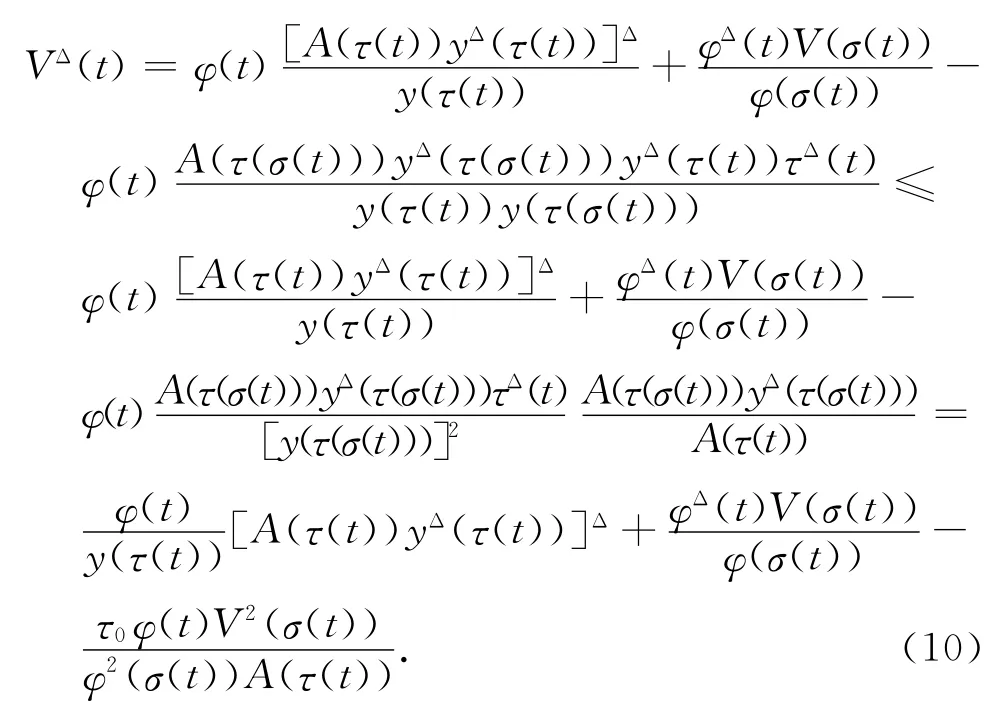
综合式（8）和（10），并依次应用式（6）及y（τ（t））≤y（τ（σ（t））），得

在式（11）中利用完全平方技巧，可得

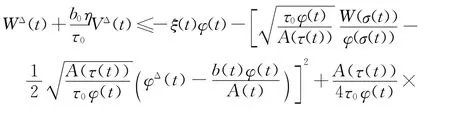
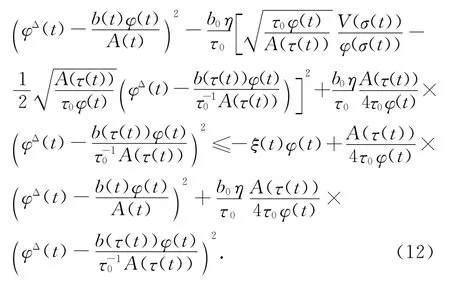
上式两边从t1到t（t≥t1）积分，得

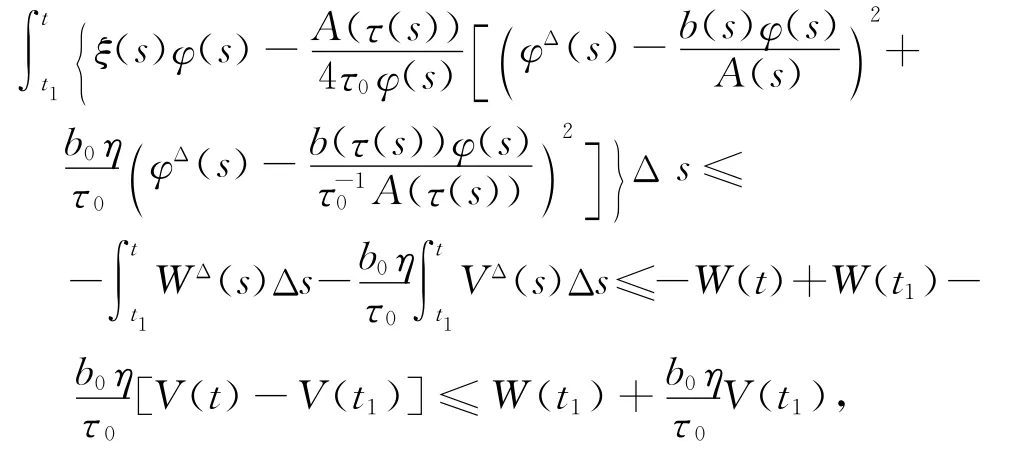
上式取t→∞的上极限，与式（3）矛盾．定理证毕．

注1 选取不同的函数φ就能得到关于动力方程（1）振动的不同判别准则．例如，在定理1中分别取φ（t）≡1，φ（t）＝t，就可分别得到如下振动性结果．

注2 若方程（1）中g（u）＝u，b（t）≡0，F（t，x（δ（t）））＝q（t）f（x（δ（t））），则由定理1即得文献［25］中的定理2．2．

下面给出动力方程（1）的Philos型振动准则．考虑集合D＝｛（t，s）：t≥s≥t0，t，s∈T｝，D0＝｛（t，s）：t＞s≥t0，t，s∈T｝，称函数H∈Ω，如果H（t，s）在D上有定义且当t≥t0时，H（t，t）＝0；H（t，s）∈Crd（D0，R），H（t，s）＞0 （t＞s），并且在D0上H（t，s）有连续且非正的偏导数，即且

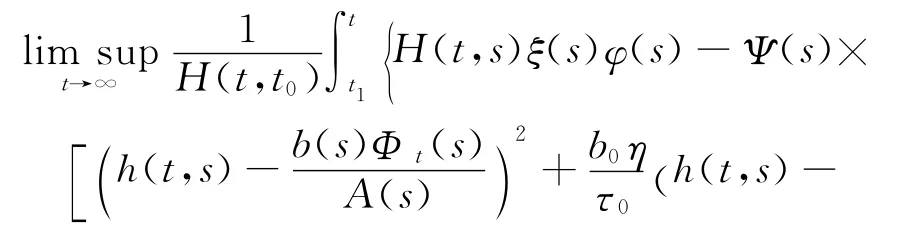
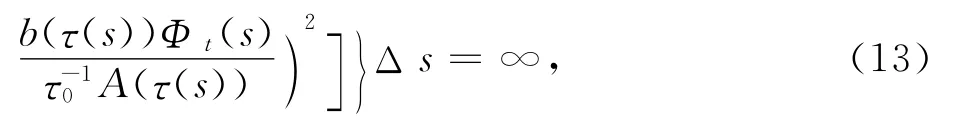
其中t1≥t0为某常数，函数ξ（t）的定义如定理1，函数h（t，s）由确定，则方程（1）在［t0，∞）T上是振动的．

证明 设方程（1）在［t0，∞）T上有一个非振动解x（t），不妨设x（t）＞0，x（τ（t））＞0，x（δ（t））＞0，t∈［t1，∞）T，t1∈［t0，∞）T，则y（t）＞0．由定理1的证明知，式（11）成立，即当s∈［t1，∞）T时，有

上式两边同乘H（t，s），并从t1到t（t≥t1）积分，应用时间模上的分部积分法，可得

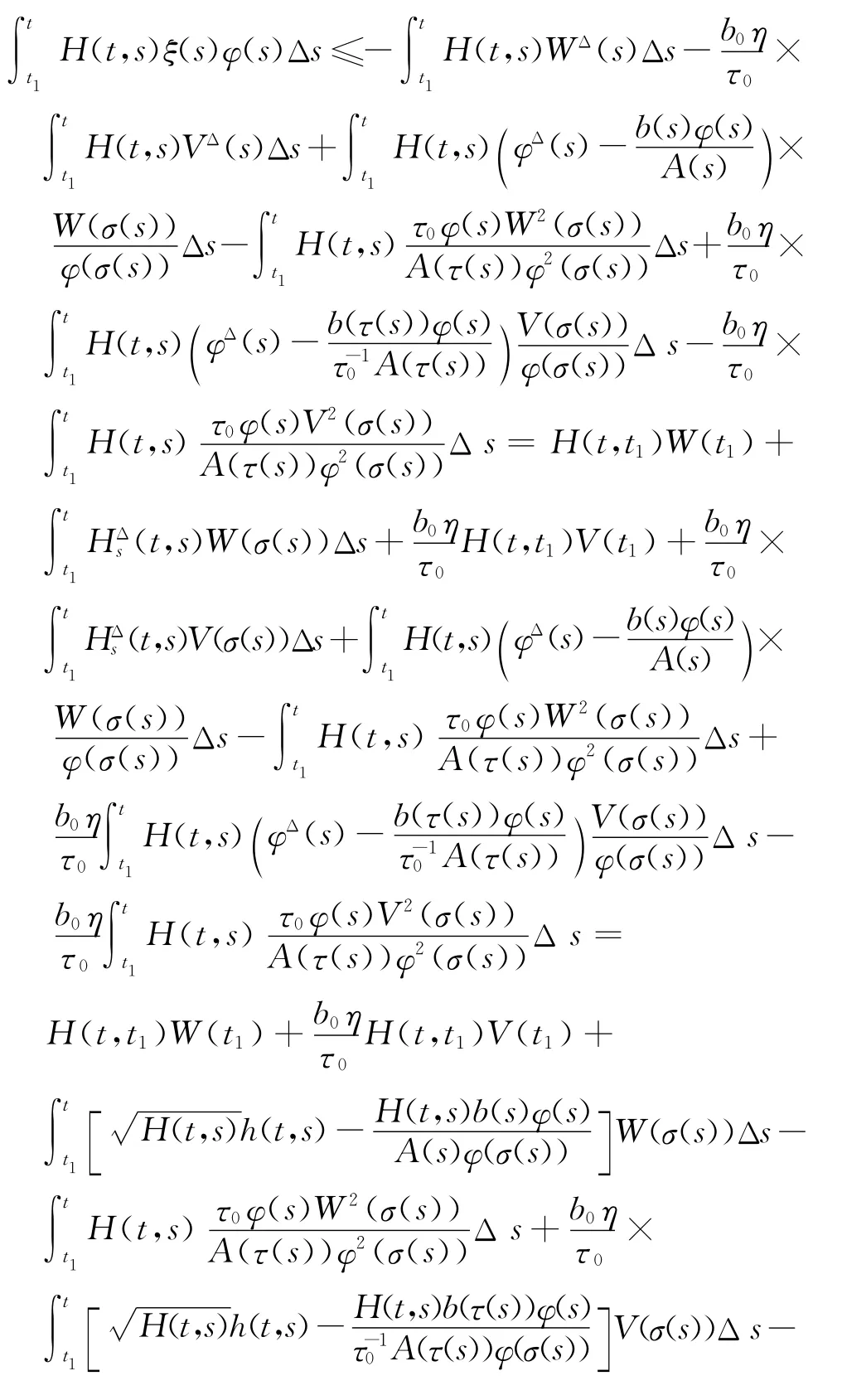
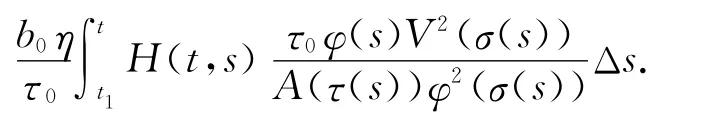
在上式中利用完全平方技巧，可得

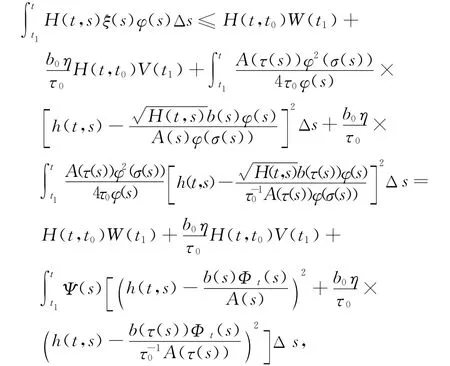
因此，

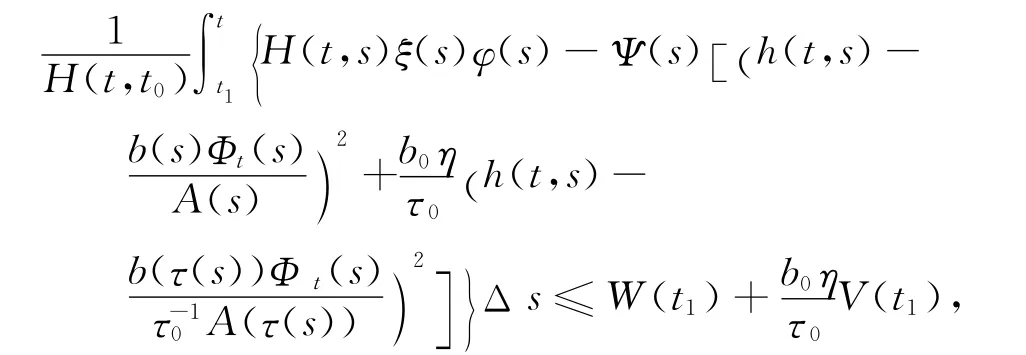
上式取t→∞的上极限，结果与式（13）矛盾，定理2证毕．

注3 通过选择恰当的参数函数H（t，s）及φ（t），同样能导出关于动力方程（1）的许多不同的振动准则．例如，H（t，s）＝（t－s）ω，或等．现取H（t，s）＝（t－s）ω，则由定理2，可以得到方程（1）的如下Kamenev型振动准则．

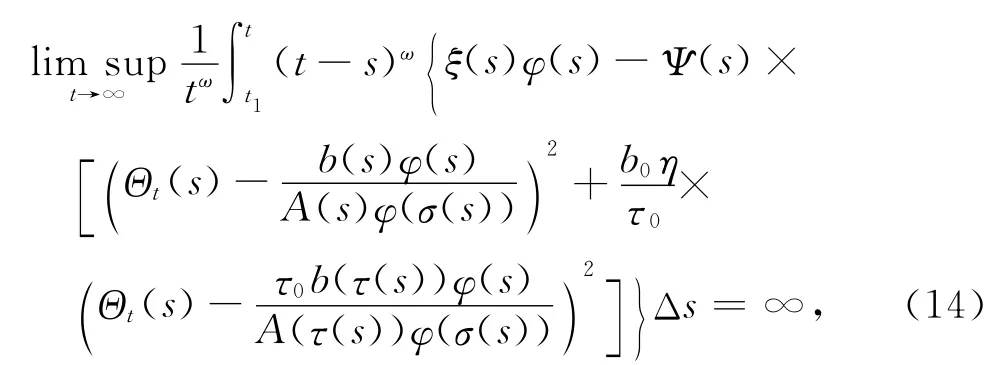
其中，t1≥t0为某常数，函数ξ（t）的定义如定理1，则方程（1）在［t0，∞）T上是振动的．

显然，本文给出的时间模T上具有阻尼项和非线性中立项的变时滞动力方程（1）振动性的新判别准则，去掉了现有文献对中立项函数的限制条件0≤p（t）＜1，应用范围更广．

2 例子与应用

例1 考虑如下二阶泛函动力方程

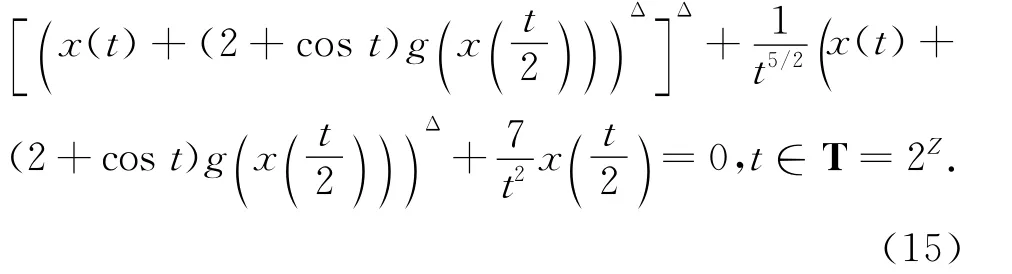
显然，方程（15）是具有非线性中立项和阻尼项的二阶2－差分方程，其中t≥t0＝2，A（t）＝1，B（t）＝

显然条件（H1）～（H6）都满足．又由于ξ（t）＝，且

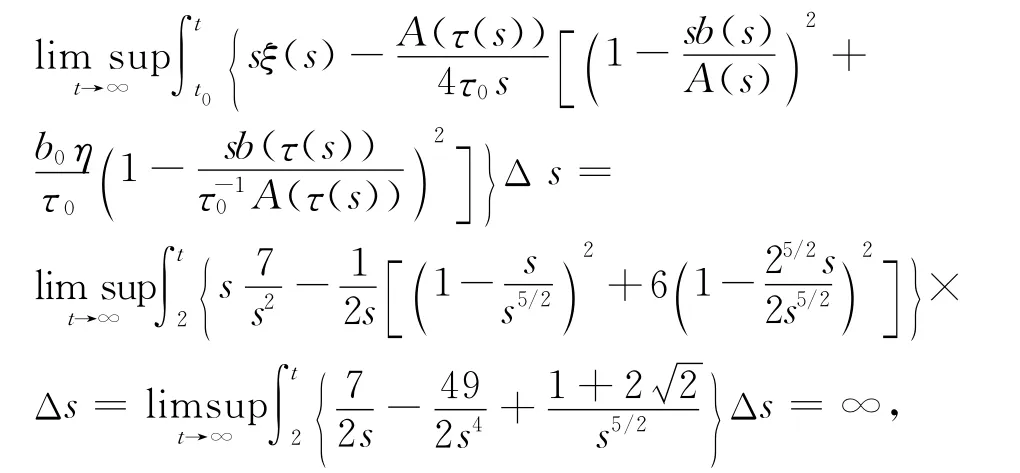
则推论2的条件全部满足，于是由推论2知，方程（15）是振动的．

注4 注意到，例题中的方程具有阻尼项和非线性中立项，且中立项的系数函数不满足0≤B（t）＜1，因此，文献［9－26，28－32］中的结论都不能用于方程（15），而文献［33－34］中的结果对具有阻尼项的方程（15）亦不适用．

3 结 论

讨论了时间模T上一类具阻尼项和非线性中立项的变滞量二阶非线性动力方程的振动性，建立了5个判别其解振动的准则，结果反映了阻尼项和中立项及变时滞在振动中的作用．这些重要结论为解决自动控制技术、物理学（如量子理论等）、经济学、生物种群动力学、伺服力学、人口学以及神经网络等领域的实际问题提供了数学理论依据和科学基础．

参考文献（References）：

［1］ RAVI P，AGARWAL R P，BOHNER M，et al．Nonoscillation and Oscillation：Theory for Functional Differential Equations［M］．New York：Marcel Dekker，2004．

［2］ BOHNER M，PETERSON A．Dynamic Equations on Time Scales，An Introduction with Applications［M］．Boston：Birkhauser，2001．

［3］ AGARWAL R P，BOHNER M，GRACE S R，et al．Discrete Oscillation Theory［M］．New York：Hindawi Publishing Corporation，2005．

［4］ ZHANG Q X，GAO L．Oscillation criteria for secondorder half－linear delay dynamic equations with damping on time scales［J］．Sci Sin Math，2010，40（7）：673－682．

［5］ SAHINER Y．Oscillation of second order delay differential equations on time scales［J］．Nonlinear Analysis：Theory，Methods ＆Applications，2005，63：1073－1080．

［6］ HAN Z L，BAO S，SUN S R．Oscillation of secondorder delay dynamic equations on time scales［J］．Journal of Applied Mathematics ＆Computing，2009，30（1）：459－468．

［7］ SUN S，HAN Z，ZHANG C．Oscillation of second order delay dynamic equations on time scales［J］．J Appl Math Comput，2009，30：459－468．

［8］ GRACE S R，AGARWAL R P，KAYMAKCALAN B，et al．Oscillation theorems for second order nonlinear dynamic equations［J］．J Appl Math Comput，2010，32：205－218．

［9］ AGARWAL R P，O’REGAN D，SAKER S H．Oscillation criteria for second－order nonlinear neutral delay dynamic equations［J］．J Math Anal Appl，2004，300：203－217．

［10］ SAKER S H．Oscillation of second－order nonlinear neutral delay dynamic equations on time scales［J］．J Comput Appl Math，2006，187：123－141．

［11］ SAHINER Y．Oscillation of second－order neutral delay and mixed－type dynamic equations on time scales ［J］．Adv Diff Eq，2006：1－9．

［12］ SAKER S H，AGARWAL R P，O’REGAN D．Oscillation results for second－order nonlinear neutral delay dynamic equations on time scales［J］．Applicable Analysis，2007，86：1－17．

［13］ WU H W，ZHUANG R K，MATHSEN R M．Oscillation criteria for second－order nonlinear neutral variable delay dynamic equations［J］．Appl Math Comput，2006，178：321－331．

［14］ SAKER S H，O’REGAN D．New oscillation criteria for second－order neutral function dynamic equation via the generalized Riccati substitution［J］．Commun Nonlinear Sci Numer Simulat，2010（16）：423－434．

［15］ SAKER S H．Oscillation of second－order neutral delay dynamic equations of Emden－Fowler type［J］．Dyn Sys Appl，2006（15）：629－644．

［16］ 韩振来，孙书荣，张承慧．时间尺度上二阶中立型时滞动力方程的振动性［J］．中山大学学报：自然科学版，2010，49（5）：21－24．HAN Zhenlai，SUN Shurong，ZHANG Chenghui．Oscillation of second－order neutral delay dynamic equations on time scales［J］．Acta Scientiarum Naturalium Universitatis Sunyatseni，2010，49（5）：21－24．

［17］ YANG J S，QIN X W，ZHANG X J．Oscillation criteria for certain second－order nonlinear neutral delay dynamic equations with damping on time scales［J］．Mathematica Applicata，2015，28（2）：439－448．

［18］ 孙一冰，韩振来，孙书荣，等．时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性［J］．应用数学学报，2013，36（3）：480－494．SUN Yibing，HAN Zhenlai，SUN Shurong，et al．Oscillation of a class of second order half－linear neutral delay dynamic equations with damping on time scales ［J］．Acta Mathematicae Applicatae Sinica，2013，36 （3）：480－494．

［19］ 杨甲山．时间测度链上具非线性中立项的二阶阻尼动力方程的振动性［J］．浙江大学学报：理学版，2012，39（3）：261－265．YANG Jiashan．Oscillation of second－order damping dynamic equation on time scales with nonlinear neutral term［J］．Journal of Zhejiang University：Science Edition，2012，39（3）：261－265．

［20］ 杨甲山，黄劲．时间模上一类二阶非线性动态方程振荡性的新准则［J］．华东师范大学学报：自然科学版，2015（3）：9－15．YANG Jiashan，HUANG Jin．New criteria for oscillation of certain second－order nonlinear dynamic equations on time scales［J］．Journal of East China Normal University：Natural Science，2015（3）：9－15．

［21］ 杨甲山，苏芳．具阻尼项的一类二阶非线性动态方程的振动准则［J］．应用数学，2014，27（2）：392－404．YANG Jiashan，SU Fang．Oscillation criteria for cer－tain second－order nonlinear dynamic equations with damping［J］．Mathematica Applicata，2014，27（2）：392－404．

［22］ 张全信，高丽，刘守华．时间尺度上具阻尼项的二阶半线性时滞动力方程的振动准则（II）［J］．中国科学：数学，2011，41（10）：885－896．ZHANG Quanxin，GAO Li，LIU Shouhua．Oscillation criteria for second－order half－linear delay dynamic equations with damping on time scales（II）［J］．SCIENTIA SINICA Mathematica，2011，41（10）：885－896．

［23］ 李同兴，韩振来．时间尺度上二阶超线性动力方程振动性［J］．济南大学学报：自然科学版，2010，24（2）：209－211．LI Tongxing，HAN Zhenlai．Oscillation for secondorder superlinar dynamic equations on time scales［J］．Journal of University of Jinan：Science and Technology，2010，24（2）：209－211．

［24］ HAN Z L，LI T X，SUN S R，et al．Oscillation for second－order nonlinear delay dynamic equations on time scales［J］．Advances in Difference Equations，2009，11（2）：10－14．

［25］ HAN Z L，LI T X，SUN S R，et al．On the oscillation of second－order neutral delay dynamic equations on time scales［J］．African Diaspora Journal of Mathematics，2010，9（1）：76－86．

［26］ CHEN D X，QU P X，LAN Y H．Oscillation of second－order nonlinear dynamic equations with positive and negative coefficients［J］．Advances in Difference Equations，2013：168

［27］ YANG J S．Oscillation criteria for certain third－order delay dynamic equations［J］．Advances in Difference Equations，2013：178．

［28］ 杨甲山，莫协强．时间模上一类二阶非线性动态方程的振动结果［J］．安徽大学学报：自然科学版，2015，39 （1）：1－7．YANG Jiashan，MO Xieqiang．Oscillation results of certain second－order nonlinear dynamic equations on time scales［J］．Journal of Anhui University：Natural Science Edition，2015，39（1）：1－7．

［29］ 潘元元，韩振来．时标上二阶中立型时滞动力方程的振动性［J］．济南大学学报：自然科学版，2012，26（2）：191－194．PAN Yuanyuan，HAN Zhenlai．Oscillation behavior of second－order neutral delay dynamic equations on time scales［J］．Journal of University of Jinan：Sci and Tech，2012，26（2）：191－194．

［30］ 杨甲山．时间测度链上具正负系数的二阶阻尼动力方程的振动准则［J］．数学物理学报，2014，34A（2）：393－408．YANG Jiashan．Oscillation criteria for second－order dynamic equations with positive and negative coefficients and damping on time scales［J］．Acta Mathematica Scientia，2014，34A（2）：393－408．

［31］ 杨甲山，苏芳．时间测度链上一类二阶动力方程的振动性［J］．数学的实践与认识，2014，44（13）：265－270．YANG Jiashan，SU Fang．Oscillation of a class of second－order dynamic equation on time scales［J］．Mathematics in Practice and Theory，2014，44（13）：265－270．

［32］ 杨甲山．时标上一类具阻尼项的二阶动态方程的振荡性［J］．系统科学与数学，2014，34（6）：734－751．YANG Jiashan．Oscillation for a class of second－order dynamic equations with damping on time scales［J］．Journal of Systems Science and Mathematical Sciences，2014，34（6）：734－751．

［33］ 杨甲山，莫协强．时间轴上一类二阶动态系统振荡的充分条件［J］．安徽大学学报：自然科学版，2014，38 （5）：1－6．YANG Jiashan，MO Xieqiang．Sufficient conditions of oscillation for certain second－order dynamic equations on time scales［J］．Journal of Anhui University：Natural Science Edition，2014，38（5）：1－6．

［34］ 张晓建，杨甲山．时间模上二阶非线性动态方程振荡性的新结果［J］．浙江大学学报：理学版，2014，41（5）：499－505．ZHANG Xiaojian，YANG Jiashan．New results of oscillation for second－order nonlinear dynamic equations on time scales［J］．Journal of Zhejiang University：Science Edition，2014，41（5）：499－505．

［35］ 曾云辉，罗李平，罗振国．具连续分布滞量的二阶半线性阻尼微分方程的振动准则［J］．振动与冲击，2013，32（8）：1－4．ZENG Yunhui，LUO Liping，LUO Zhenguo．Oscillation criteria of a second order half－linear damped differential equation with distributed deviating argument ［J］．Journal of Vibration and Shock，2013，32（8）：1－4．

Oscillation analysis of certain second－order nonlinear damped dynamic equations on time scales

YANG Jiashan，TAN Weiming，QIN Xuewen，SU Fang（School of Information and Electronic Engineering，Wuzhou University，Wuzhou 543002，Guangxi Zhuang Autonomous Region，China）

Jo urnal of Zhejiang University（Science Edition），2016，43（1）：064－070

Abstract：This paper studies the oscillations of a class of second－order nonlinear neutral variable delay dynamic equations with a dampling term on a arbitrary time scale T．By using the calculus theory on time scales and the inequality technique，as well as the generalized Riccati transformation and the method of Hfunction，five oscillation theorems for the equations are presented．In particular，the Hille type and Kamenev－type oscillation criteria obtained can ectend and improve some known results in other literatures．An example is given to illustrate that the assumptions in our theorems are less restrictive．

Key Words：oscillation；time scales；delay dynamic equations；damping term；nonlinear neutral term

作者简介：杨甲山（1963－），男，硕士，教授，主要从事微分差分方程与动力学方程研究，E－mail：syxyyjs＠163．com．

基金项目：广西壮族自治区教育厅科研基金项目（2013YB223）；湖南省科技厅科研基金项目（2012FJ3107）；梧州学院2014年校级科研重大项目（2014A003）；硕士学会授予单位立项建设项目（桂学会［2013］4号）．

收稿日期：2014－12－26．

DOI：10．3785／j．issn．1008－9497．2016．01．011

中图分类号：O 175．7

文献标志码：A

文章编号：1008－9497（2016）01－064－07