基于多边形布尔运算的卫星区域覆盖分析算法

汪荣峰

(装备学院 航天指挥系, 北京 101416)



基于多边形布尔运算的卫星区域覆盖分析算法

汪荣峰

(装备学院 航天指挥系, 北京 101416)

摘要传统网格点法计算卫星区域覆盖性能的精度受网格大小影响且效率低，为此提出了一种基于多边形布尔运算的新算法。算法在计算卫星覆盖带与待分析区域相交多边形的基础上，基于多边形交、差运算，将覆盖多边形分解为具有单一覆盖属性的组成部分；将分解结果三角化后利用球面三角形面积公式计算面积；最后统计面积以计算覆盖率，并设计实现了分类统计方式和可视化表现方法。与传统网格点法相比，该算法覆盖率计算结果稳定，不受类似网格大小之类因素影响，在接近精度情况下效率比网格点法提高约20倍。

关键词卫星；区域覆盖；布尔运算；三角化；覆盖率

卫星区域覆盖分析对于卫星任务规划[1]、星座设计[2]等都具有非常重要的意义，其主要任务是计算单颗或多颗卫星(星座)在给定时间范围对待分析区域的覆盖率、覆盖次数、总覆盖时间、平均覆盖时间、最大覆盖间隔、平均覆盖间隔等指标[3]，其中覆盖率是核心指标。

卫星区域覆盖分析方法主要有解析法、网格点法和基于几何运算的方法。解析法[4]是基于卫星与地球的几何关系直接得到覆盖面积计算的解析公式，这种方法只适于单颗卫星覆盖性能分析，且待分析区域必须包含卫星覆盖范围。

目前最常用的是网格点法[5-6]，待分析区域划分为一系列网格(可按经纬度、距离和面积划分网格点)，对于每颗卫星按一定步长计算其覆盖网格，根据覆盖网格数与总网格数的关系得到覆盖率等指标。这种方法易于实现、应用广泛，且可以避免重合覆盖区域的多次统计，但计算量大、重复计算多、计算结果受网格大小影响，基于网格交点和按一定步长的计算方式都有可能导致误判。秦睿杰等[7]提出了网格中抽样的快速算法，但精度会受到一定影响。

白萌等[8]将卫星瞬时覆盖投影到二维平面上形成覆盖多边形，通过多边形并运算获得总的覆盖多边形，从而得到总瞬时覆盖率。该方法效率高，且计算得到的面积较为精确，但只适于瞬时覆盖分析，且只能得到总覆盖率，无法得到覆盖次数等其他信息。

本文算法通过计算出卫星在经纬度平面上覆盖带与待分析区域的相交多边形，一方面减少了网格点法中各步长覆盖之间的重复计算，另一方面消除了步长取值过大所导致的漏判。通过多边形交、差运算将区域覆盖多边形划分为具有单一覆盖属性的子多边形，算法不但可用于瞬时覆盖分析，也可用于一段时间的覆盖分析；不但可计算总覆盖率，也可计算各卫星覆盖率、覆盖次数等其他关键指标。算法的时间复杂度与分解后多边形数有关，而不像网格点法取决于划分的网格数目，效率更高。在覆盖面积和覆盖率的计算上，采用多边形三角剖分之后运用球面三角形面积公式计算的方法，计算结果稳定，不像网格法会受到网格大小之类因素影响。

1待分析区域内卫星覆盖多边形的计算

待分析区域往往以经纬度坐标给定，在经纬度平面上既可能是规则矩形，也可能是复杂多边形，如某个国家或地区。卫星飞行过程中只有有限时间经过该区域，首先计算这段时间形成的覆盖多边形。

卫星传感器覆盖其星下点周围一定范围，沿卫星飞行方向在地球表面形成覆盖带，如图1a)所示。根据卫星位置，计算覆盖带两侧点的经纬度坐标，如图1a)中a、b、c、d点。根据卫星位置和覆盖角，构造三维空间中射线，计算该射线与地球表面的交点，根据交点坐标反算其经纬度；卫星轨道高、覆盖角大时，射线可能与地球表面无交，此时构造经过该射线和地球中心的平面，以该平面与地球表面的切点作为覆盖带边界点。得到覆盖带在经纬度平面的投影，如图1b)所示。

首先利用多边形求交算法计算相交覆盖带，对于卫星轨道上每个采样点，算法为：

Step1利用该采样点的2个覆盖边界点和下一采样点的覆盖边界点构造一四边形；

Step2如果四边形与待分析区域有交，转Step3，否则转Step5；

Step3如果没有已形成的相交区域，构造2个空的点表leftpts和rightpts；

Step4将边界点分别输出到leftpts和rightpts中，转Step1；

Step5如果leftpts和rightpts不为空，合并leftpts和rightpts为多边形并输出，转Step1。

以图1b)为例，开始AabB与区域12345无交，继续下一个；BbcC与12345有交，则将BC输出到leftpts中，bc输出到rightpts中；依次处理，分别将DEFG加入到leftpts，defg加入到rightpts中；GghH不再与12345有交，则将leftpts和rightpts合并为bcdefgGFEDCB，即为相交的覆盖带。

上述算法中，对轨道上第1个和最后1个采样点，要根据传感器类型进行特殊处理。如为圆锥形传感器，则需在对应方向加入半圆(离散为多边形)；如为四棱锥形传感器，则需在对应方向扩展出2个点。

a) 卫星覆盖带

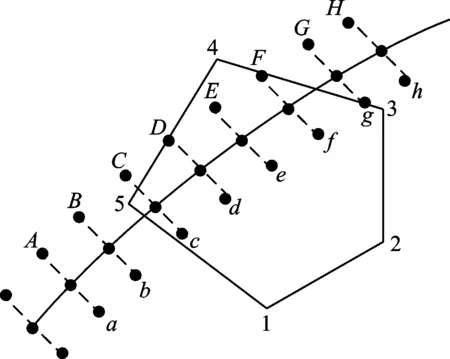
b) 卫星覆盖经纬度投影与待分析区域图1　与待分析区域有交的卫星覆盖带计算

上述算法仅得到与待分析区域有交的覆盖带，还非实际的区域内覆盖，如图2a)所示，还须将得到的多边形与待分析区域求交，得到区域内覆盖多边形，如图2b)所示。如果待分析区域跨越180°经度，将其以180°经度为界分解为2个或多个区域，然后再应用本文算法求解。

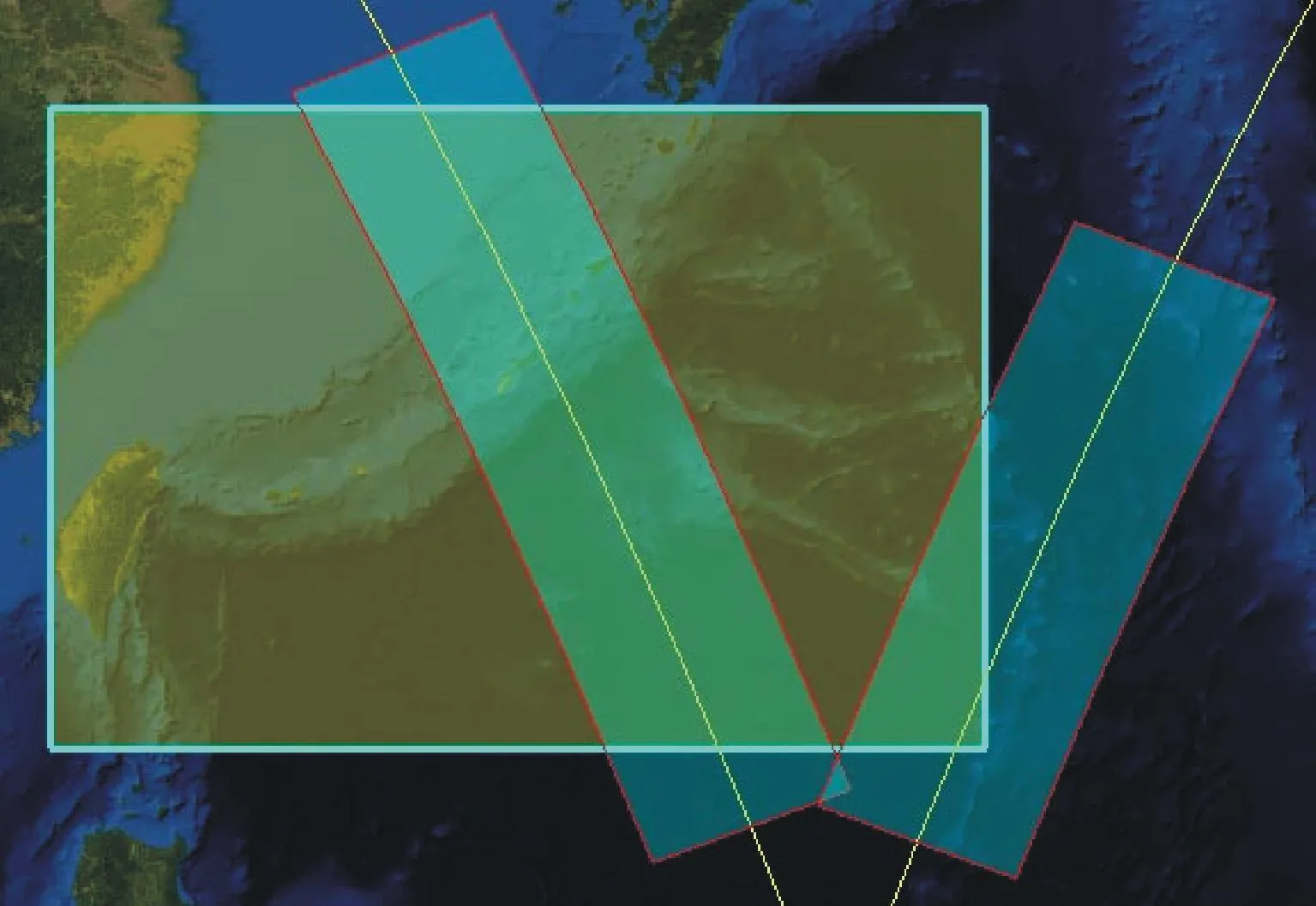
a) 相交覆盖带

b) 区域覆盖多边形图2　区域内覆盖多边形计算

2区域覆盖多边形分解与面积计算

经过第1节处理，得到的相交多边形并不能直接计算覆盖率，因为存在区域被多颗卫星覆盖，或者被同一卫星多次覆盖等情况，即多边形存在复杂的相交情况。如果仅仅计算总覆盖率1个指标，可以通过计算所有多边形的并,然后计算其面积来实现。为了支持其他指标的计算，将这些相交多边形分解为独立的具有单一覆盖属性的小多边形，即分解后的每个小多边形覆盖次数、覆盖卫星等情况一致。

如图3所示，ABCD和abcd为一颗卫星的覆盖，EFGH为另一颗卫星的覆盖，三者之间都存在相交关系，需分解为单一覆盖性质的小多边形。AE21、1bB、5cF、a47d为仅被第1颗卫星覆盖的区域；DH43、CG76为仅被第2颗卫星覆盖的区域；ED32、FC65为被第1颗和第2颗卫星同时覆盖的部分；125cB为被第1颗卫星2次覆盖的区域；2365则是被第1颗卫星覆盖2次、第2颗卫星覆盖1次的区域。

图3　相交多边形分解示意图

基于多边形交、差运算进行覆盖多边形分解，任意2多边形之间关系分为4种：

1) 2多边形无交，不必特殊处理，当多边形与所有其他多边形都无交的时候，该多边形已是分解最终结果，输出。

2) 2多边形有交，且交与2多边形均不重合，如图4a)所示，ABCD和abcd2个多边形。首先计算得到交1234，其覆盖属性为2多边形属性的和；然后计算ABCD与abcd的差，得到A14D和BC32；最后计算abcd与ABCD的差，得到bc21和da43，差的覆盖属性仍维持原来的值。

3) 2多边形的交为第1个多边形，如图4b)所示，多边形AabD与ABCD求交，结果为AabD。此时首先将AabD的覆盖属性改为2多边形覆盖属性之和；然后计算第2个多边形与第1个多边形之差，得到BCba，其覆盖属性维持不变。

4) 2多边形的交为第2个多边形，与第3)种情况类似处理。多边形的覆盖属性定义为一个数组，每一项包括覆盖的卫星、分辨率等各种指标，覆盖属性合并即为该数组的合并。

a) 交不等于输入多边形　　　　b) 交等于第1个多边形图4　2多边形相交关系

通过一个先进先出队列来实现覆盖多边形分解，首先将第1节计算得到的覆盖多边形加入队列，然后以队列是否为空来控制循环，执行如下逻辑：取出队列中第1个多边形；判断该多边形与队列中所有其他多边形的关系，如果均无交，则输出；否则按上1段的描述生成新多边形并加入到队尾。

以上算法中，需使用多边形交、差布尔运算，由于各多边形相交情况复杂，布尔运算组合情况多，因此在多次运算后会出现多边形有公共点、公共边的情形，对算法稳定性要求高，因此使用开源几何引擎(Geometry Engine Open Source，GEOS)作为多边形布尔运算工具。而在第1部分的相交覆盖带计算算法中，不存在上述奇异情况，但对卫星轨道上每个采样点都需应用多边形求交运算，效率要求高，使用效率更高的算法[9]。

不同于网格点法以网格数比值来表示覆盖率，本文算法通过计算每个分解多边形的面积来实现。采用的方法是：首先将多边形三角化，然后将其反算到地球表面，使用球面三角形面积公式进行计算。

使用OpenGL的GLU辅助库中的GLUtesselator来实现多边形三角化。GLUtesselator对多边形剖分的结果是OpenGL中的基本图元，而并非都是三角形。因此，通过其回调函数记录剖分结果之后，再根据图元类型(包括三角形扇、三角形带、矩形、凸多边形等)，将其转化为三角形。

虽然也有椭球面三角形面积的计算算法[10]，但是其计算复杂、计算量大，对地球采用球形近似对精度影响很小，因此采用球面三角形面积计算公式[11]

(1)

式中：S为三角形球面面积；A、B、C分别为球面三角形的3个内角(大圆弧在交点处切线的夹角)；R为地球半径。内角计算方法为：根据顶点经纬度坐标计算地心坐标，过地心到顶点构造单位矢量；每2个矢量计算矢量积得到大圆平面的法向量；通过单位法向量的数量积，反余弦计算得到内角。

3精度效率分析及可视化表达方式设计

通过统计分解后的多边形信息，得到区域覆盖率等指标。累加所有分解多边形的面积，得到总覆盖面积；将待分析区域三角化后，计算得到区域总面积；以总覆盖面积除以总面积，得到覆盖率。

首先对本文算法和网格点法的效率进行简单的理论分析。极端情况下，任意2个卫星覆盖条带都有交，相交多边形为n2量级，此时多边形布尔运算次数为n3量级；对于网格点法，卫星个数为n，网格划分为m，采用判断覆盖条带与网格关系的方法(原始网格点法是针对卫星轨道上每个采样点，对所有网格进行判断，非常耗时，但可以记录每个网格的时间信息尤其是持续信息，这是本文算法和采用覆盖条带与网格相交关系方法无法支持的)，其运算量为nm。有2个条件决定了本文算法的效率优势：一是卫星区域覆盖分析一般针对星座或有限多颗卫星进行(一方面n值有限(20～30)，另一方面这些卫星轨道具有一定的相关性，任意2个覆盖带都相交的极端情况出现的可能性非常小)；二是m的值远远大于n，如对于经纬度范围1°左右的区域，按1 km划分网格，其m值约为10 000，即nm远大于n3。

对东经110°～130°，北纬35°～45°之间的区域，分析12颗卫星(两行轨道根数略，覆盖角均为5°)在20140501T080000时刻开始24 h的覆盖情况，网格点法和本文算法得到的覆盖率及用时如表1所示。

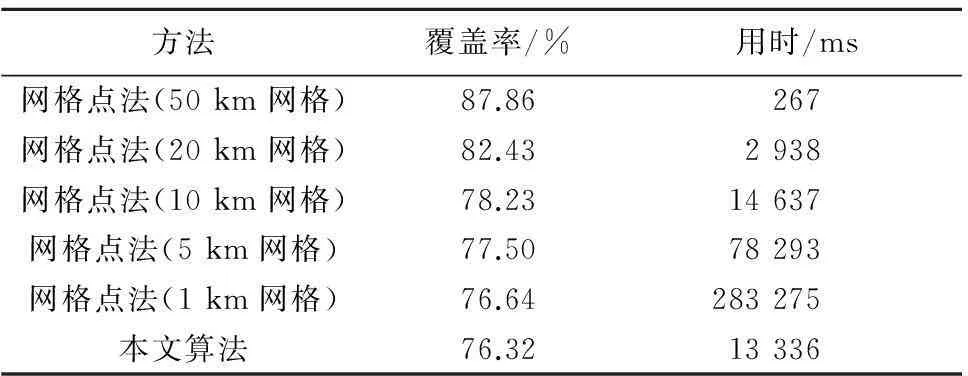
表1　网格点法和本文算法覆盖率计算结果及用时对比

可以看出，网格点法计算精度受到网格大小的影响。在本算例中，网格大小约为1 km时，其精度才接近本文算法。在算法效率方面，本文算法用时与网格大小为10 km左右时接近，而与精度接近的1 km网格相比，用时不到网格点法的1/20。需要说明的是，本文算法对比所用的网格点法实现中，已经采用了本文算法第1部分的技术对卫星轨道采样点进行了快速排除，否则其效率更低。

除了覆盖面积，总覆盖率之外，还可以根据多边形覆盖属性得到分类统计信息：按覆盖次数统计，根据多边形由几个原始多边形相交得到，可知其覆盖次数，将相同覆盖次数的所有多边形面积相加，得到统计结果；按卫星统计，首先遍历所有多边形，确定其覆盖卫星组合，然后就每种组合累加相应多边形面积。此外，可以支持按分辨率、频段等各种统计方式。

设计实现了柱形图和饼图2种统计结果可视化表现形式，显示总面积、覆盖面积、图例等信息，并以柱形图和饼图形式显示各种卫星组合、覆盖次数的覆盖面积与百分比等。

4结 束 语

与网格点法相比，本文提出算法在覆盖面积和覆盖率计算的精度和效率方面有明显优势，存在的主要不足有3点：

1) 无法支持总覆盖时间、平均覆盖时间等与时间有关指标的分析，这是由于网格点法可以将时间作为网格的属性，但是本文算法使用的多边形大小不一，无法做此处理，应用中相应指标可以通过对地面目标的覆盖时间窗口分析技术来获得；

2) 采用的面积计算方法，假定地球为球形，与应用椭球模型或地理投影方式相比，存在可忽略的微小误差；

3) 当卫星轨道倾角很大，地表覆盖带很宽，且待分析区域也在高纬度地区时，星下线转折相对陡峭，算法第1步中，星下线两侧点位置关系可能错乱，如图1中Aa、Bb、Cc可能相交，此时生成的覆盖多边形有时不再是简单多边形，结果不再准确。

参考文献(References)

[1]王慧林,邱涤珊,黄小军，等.面向区域覆盖的电子侦察卫星规划方法研究[J].兵工学报,2011,32(11):1365-1372.

[2]曾德林.快速响应小卫星星座设计及覆盖性能仿真分析[J].计算机仿真,2014,31(6):73-77.

[3]刘文,张育林.区域覆盖低轨卫星移动通信系统星座优化设计[J].上海航天,2007(4):43-47.

[4]张润.基于重访周期的对地侦察小卫星星座设计[D].西安:西安电子科技大学,2011:23-32.

[5]马吉康.通信卫星组网仿真系统的设计与实现[D].北京: 北京邮电大学,2008:18-23.

[6]沈欣.光学遥感卫星轨道设计若干关键技术研究[D]. 武汉:武汉大学, 2012:67-68.

[7]秦睿杰,戴光明,王茂才，等.一种计算星座区域覆盖率的高效抽样网格点法[J].计算机应用研究,2015,32(4):65-68.

[8]白萌,李大林,陈梦云.卫星对地覆盖区域的融合算法研究[C]//中国空间科学学会.第二十三届全国空间探测学术交流会论文集.厦门:中国空间科学学会,2010：341-346.

[9]汪荣峰,廖学军.格网划分的双策略跟踪多边形裁剪算法[J].图学学报,2012,33(6):45-49.

[10]施一民,朱紫阳.利用测地坐标计算椭球面上凸多边形面积的算法研究[J].同济大学学报(自然科学版),2006,36(4):504-507.

[11]张楚宾.球面三角学[M].北京:人民教育出版社,1978:52-53.

(编辑：李江涛)

Analysis Algorithm for Satellite Regional Coverage Based on Polygonal Boolean Operation

WANG Rongfeng

(Department of Space Command, Equipment Academy, Beijing 101416, China)

AbstractTraditional mesh point calculation of satellite regional coverage is affected by the grid size in precision and inefficient, so the author proposes a new algorithm based on polygonal Boolean operation. With this algorithm, based on the calculation of polygons formed by the intersection of coverage area and the zone to be analyzed, by using polygonal intersection and subtraction operation, the author decomposes the coverage polygon into many components with single attribute of coverage; and then, the author triangulates the decomposition result and calculates the area with spherical triangle area formula; in the end, the author calculates the area to obtain the coverage and realizes the categorization-based statistic method and visualized presentation method through deliberate design. Comparing with traditional mesh point method, this algorithm can draw stable result, free of influence of factors like size of grid and its efficiency is approx. 20 times of that of mesh point method when similar accuracy .

Keywordssatellite; regional coverage; Boolean operation; triangulation; coverage ratio

文献标志码A DOI10.3783/j.issn.2095-3828.2016.02.019

文章编号2095-3828(2016)02-0083-05

中图分类号TP391.9

作者简介汪荣峰(1973-),男，副教授，主要研究方向为空间态势与分析。wrflly@163.com

收稿日期2015-07-21