井下管柱的真实轴向力计算与应用

冯 定，王 杰，钱利勤，孙巧雷，张 红，涂亿柳长江大学机械工程学院，湖北 荆州湖北省油气钻完井工具工程技术研究中心，湖北 荆州非常规油气湖北省协同创新中心(长江大学)，湖北 武汉

井下管柱的真实轴向力计算与应用

冯 定1,2,3，王 杰1,2,3，钱利勤1,2,3，孙巧雷1,2,3，张 红1,2,3，涂亿柳1,2,31
1长江大学机械工程学院，湖北 荆州2湖北省油气钻完井工具工程技术研究中心，湖北 荆州3非常规油气湖北省协同创新中心(长江大学)，湖北 武汉

http://dx.doi.org/10.12677/jogt.2016.383027

Received: Mar. 10th, 2016; accepted: Apr. 15th, 2016; published: Sep. 15th, 2016

Copyright © 2016 by authors, Yangtze University and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

管柱的摩阻计算精度直接关系到完井的质量。国内外学者已经建立了许多管柱摩阻计算模型，其中“刚杆模型”是较为常用的计算模型，但是该模型在计算管柱微元体所受的浮力时，没有考虑到微元体的端面不受液体的静压力，导致所计算的轴向力为有效轴向力。对于只有侧面与液体接触的管柱单元，如果仍把排开液体的重力作为浮力，此时会在管柱单元的两端产生附加轴向力，将在此基础上计算管柱的真实轴向力，得出新的计算公式，提高管柱摩阻的计算精度。为验证模型的准确性，同时采用现有的刚杆模型和笔者所建立的模型，利用Matlab编程求解某一实际井的注水管柱在上提时的受力情况，并将两个模型所求的结果进行比较，发现建立的模型计算结果显示管柱存在中性点，中性点以下受压，中性点以上受拉，该结果与管柱的实际受力情况相符。

刚杆模型，有效轴向力，真实轴向力，附加轴向力，中性点

1. 引言

目前，国内外专家学者对复杂结构井管柱的摩阻问题进行了大量的研究，建立了很多力学模型。1983年Johansick [1]首次提出了钻柱在全井的受力情况，并根据管柱微元段力学平衡推导出了理想化的拉力-扭矩计算公式，对管柱力学研究具有一定的指导意义。1986年Sheppard等[2]在井眼轨道设计时考虑了摩阻扭矩的影响，并在Johansick建立的模型上考虑了钻井液内外压差的作用，对轴向力进行了校正。Maida等[3]在前人的基础之上又建立了二维和三维的理论模型，并且考虑了井眼轨迹在空间上的变化以及钻井液对管柱摩阻的影响。以上3人建立的管柱力学模型都没有考虑管柱的弯曲产生的影响。H.-S. Ho等[4]在钻柱摩阻方面的研究有了重大突破，他所建立的刚杆模型考虑了管柱刚度对轴向力的影响，该模型与实际更接近。国内专家也对管柱力学做出了许多贡献，建立了一系列摩阻计算模型。张建群等[5]认为钻柱侧向力受钻柱拉力的影响，于是在Johansick建立的模型基础之上又建立了新的模型。1993年韩志勇[6]建立了钻柱摩阻的“斜面圆弧”和“圆柱螺线”2种三维模型。李子丰等[7]建立的模型考虑了钻柱在井眼中的运动状态以及钻井液的影响，在一定程度上克服了刚杆模型的不足。马善洲等[8]着重考虑了管柱与井壁的接触情况，并根据不同的接触情况建立了相应的计算方法。1999年眭满仓等[9]对水平井的水平段、造斜段和稳斜段分别建立了力学模型，能较好地反映实际情况。高德利等[10]认为井下摩阻和扭矩是影响大位移井设计与施工的两个关键因素，为此建立了通用的井下摩阻和扭矩计算模型和算法。2006年，秦永和等[11]建立了一种大位移井摩阻扭矩力学分析模型，该模型主要特点在于对井眼轨迹曲率不同的部分以及钻柱刚度不同的部分分别采用纵横弯曲梁模型、软绳模型和刚杆模型。檀朝东等[12]采用管柱动力学的原理和方法建立了可用于大位移水平井生产、作业管柱的设计与校核方法，能较准确地预测管柱动态载荷。宋执武等[13]在已有的模型基础之上推导出了一套新的考虑了井眼间隙的摩阻与扭矩计算公式，该模型为合理地确定减扭接或钻杆保护器等工具在钻柱的安放位置提供更准确的依据。王志国等[14]分别考虑了井眼内安装扶正器和不安装扶正器时管柱的受力变形，为固井下套管摩阻的预测提供了参考依据。

综合现有的管柱摩阻计算模型主要包括“软绳模型”和“刚杆模型”两种，为提高计算精度，皆在此基础之上作相应修改，使模型更符合管柱的实际情况。对于短半径的复杂结构井，由于造斜段曲率半径的减小，管柱的刚性成为不可忽略的因素[15]，刚杆模型得到更广泛的认可。笔者的目的在于修正“刚杆模型”中的浮力，因为该模型在考虑管柱单元的受力时，仍以排开液体的重力作为该单元体的浮力，但是管柱单元只有侧面与液体接触，所以该方法不能真实地反映出管柱的受力情况。将在现有的刚杆模型基础之上计算管柱的真实轴向力并建立新的管柱摩阻计算模型。同时借助Matlab软件编程求解某一实际大位移井的管柱受力，并与现有的刚杆模型计算的结果相比较。

2. 管柱单元所受浮力的等效原理

对于完全浸没在液体中的一段管柱受力(图1)，管柱的外表面均与液体接触，故受到液体垂直壁面向里的压力，所有压力的矢量和即为该段管柱的浮力Ff，已知物体所受浮力为其排开液体的重力，计算公式为：

式中：Fs、Fs、Fl分别为液体对管柱单元侧面(包括内侧面和外侧面)、上、下端面的力，N；ρ为液体的密度，kg/m3；g为重力加速度，取9.8 N/kg；V为物体排开液体的体积或者物体的体积(当物体完全浸没在液体时)，m3。

浮力大小：

Figure 1. The force of pipe string completely immersed in liquid图1. 完全浸没在液体中的管柱受力

假设同样一段管柱也完全浸没在液体中，但该段管柱中的上下端面不与液体接触，即上下端面不受到液体的压力，受力情况如图2所示，该管柱单元受液体压力的合力为F。此时，根据式(1)可得：

所以，如果假设该段管柱的浮力不变，根据受力平衡，此时会在其端面产生附加轴向力(图3)。该轴向力垂直端面向外，大小与该端面和液体接触时受到液体的压力相等。由于端面上各点的位置在垂直方向上变化不大，则附加轴向力可以用集中力FU和FD来等效代替(图4)，即：

式中：A为端面面积，m2；hU、hD分别为上下端面的平均垂深，m。

Figure 2. The force of pipe string as both ends without contacting the liquid图2. 两端面不与液体接触时管柱受力

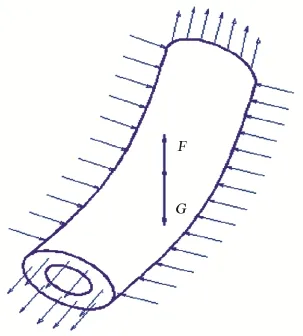
Figure 3. The additional axial force generated by buoyancy图3. 浮力产生附加轴向力

Figure 4. The additional axial force equivalent to the concentrated force图4. 附加轴向力等效成集中力

3. 管柱受力模型的建立

在模型中，将整个管柱分为若干个单元段，通过对每个管柱单元进行受力分析求出管柱在下入或上提过程中所受到的摩擦阻力。为了建立力学模型，对管柱在井眼中的情况需作适当简化，假设如下：

①套管柱处于线弹性变形状态；②套管与井壁连续接触，套管轴线与井眼轴线一致；③井壁为刚性；④计算一段套管的曲率是常数；⑤管柱截面为圆形或圆环形；⑥井内流体密度为常数，宾汉流体；⑦摩擦系数在某一口井或某一井段为常数；⑧管柱单元所受重力、正压力、摩擦力均匀分布。

3.1. 管柱单元受力模型受力分析

为建立实际管柱单元的受力模型，须建立直角坐标系ONED。原点O取在井口处，N轴向北，单位矢量为i；E轴向东，单位矢量为j；D轴向下，单位矢量为k。

建立自然曲线坐标系(et，eb，en)，其中t、n、b分别为管柱轴线的切线方向、主法线方向和副法线方向的单位向量。在井眼轴线坐标系上任取一弧长为ds的单元体AB，并对其进行受力分析。以A点为起始点，其轴线坐标为s；B点为终点，其轴线坐标为s+ds。该单元体的受力如图5所示。

对于管柱中间某一单元体仅侧面受到液体压力，假设其浮力为排开液体的重力则单元体的上、下端面的附加轴向力分别为FU(s)和FD(s)，方向垂直端面向外。其中：

式中：V为该段管柱单元的体积，m3；A为该段管柱单元端面的面积，m2；hU(s)、hD(s)分别为上、下端面的平均深度，m。

Figure 5. The force of pipe string unit图5. 管柱单元受力图

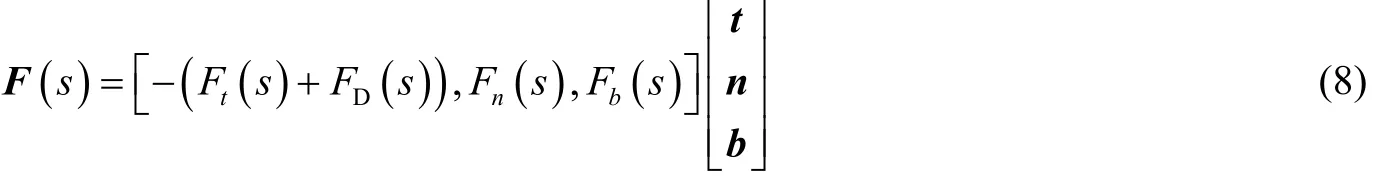
式中：Ft、Fn、Fb分别为管柱切线、主法线、副法线方向上的力，N。

式中：Mt、Mn、Mb分别为管柱轴向、主法线、副法线方向上的力矩，N·m。

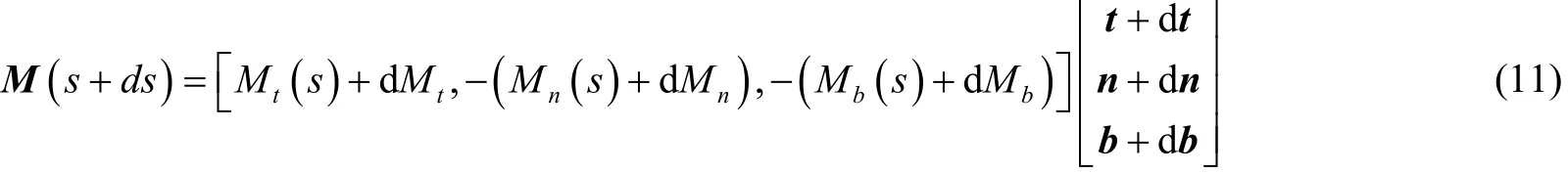
式中：N为井壁对管柱的接触压力，N/m；Nn为主法线方向的均布接触压力，N/m；Nb为副法线方向的均布接触压力，N/m；μα为轴向摩擦系数，1；“±”代表上提和下放管柱，上提管柱时取“−”，下放管柱时取“+”。

单位长度管柱浮重qr为：

式中：qr为单位长度管柱浮重，N；kf为浮力系数，1；rm为钻井液密度，kg/m3；rs为管柱材料密度，kg/m3；qm为管柱单位长度自重，N/m；g为重力的方向。

3.2. 平衡方程

由微元体ds的受力平衡条件，即合力为零可得：

将式(8)、(10)、(12)、(13)代入式(15)并整理得：

根据Frenetic-Serret公式和自然曲线坐标的单位向量与直角坐标系之间的关系[17]将式(16)进行整理，然后将力分别向切线方向、主法线和副法线投影，可得到：

式中：α为井斜角，rad；ϕ为方位角，rad；K为曲率，m−1；τ为挠率，m−1；Kα为井斜角变化率，rad/m；Kϕ为方位角变化率，rad/m。其中：

由管柱单元ds的力矩平衡[18]可得：

式中：tµ为周向摩擦系数，1；R为管柱外径，m。

将式(21)代入方程组(17)并整理可得全刚度管柱摩阻计算公式为：

其中挠率和曲率的计算[18]如下：

3.3. 边界条件

当上提和下放管柱时，对于管柱最底部单元体，其下端面与液体接触受到液体的压力，则有：

3.4. 模型的求解

式(2～26)为非线性方程组，这里采用牛顿迭代法求解，首先应用有限差分中的差分公式：

把常微分方程离散化，可先求得各端面的弯矩Mb(s)然后将其代入方程组求解，得出井底单元主法线和副法线方向上的均布接触力后，然后计算出该单元体上端面的轴向力，依次迭代即可计算出距任意井深处的上端面轴向力，管柱与井壁的接触力、摩擦力、大钩载荷。为简化计算，采用 Matlab编程求解，以井眼轨迹数据为节点，把井下管柱分成单元，即任意两个测斜数据点之间的管柱为一个单元。基本求解步骤：①读入井眼测斜数据；②根据测斜数据求出管柱单元的全角变化、井斜角变化、方位角变化、平均井斜角，平均方位角、截面弯矩，查取该单元所在位置的摩擦系数；③根据测斜数据利用最小曲率法计算出各节点的垂直深度；④根据边界条件，分别求出该单元的法向和副法向的侧向力以及上端面的轴向力；⑤重复步骤 4，依次求出全井段的摩擦力、各管柱单元的法向和副法向侧向力以及端面的轴向力；⑥将求得的结果绘制成图表。

4. 实例应用

结合现有刚杆模型和笔者建立的模型，编写Matlab程序计算某一实际井在上提注水管柱时管柱的受力情况，由于在上提套管时一般不驱动套管旋转，所以不用考虑扭矩的影响，即Mt= 0，同时由于将井段假设为空间斜面上的圆弧，则挠率τ=0。该井眼数据：井底垂深3586.60 m，水平位移1025.67 m，水垂比0.286，最大井斜角50.7˚。

井眼轨迹三维示意图如图6所示。计算结果如图7～10所示。通过对比发现，两模型计算的摩擦力总体差别不大，但是现有刚杆模型计算表明管柱在各点位置均受拉，最大轴向拉力即大钩载荷为838,960 N；而笔者模型的计算结果表明管柱存在中性点，即中性点以下管柱受压，中性点以上管柱受拉，大钩载荷为838,330 N。同时计算结果还表明，由于管柱存在受压的情况，也就导致了管柱的伸长量并非随着井深线性增加。综合以上结果，笔者建立的复杂结构井的管柱摩阻计算刚杆模型更能反映出管柱受力实际情况。

Figure 6. 3D graph of the well trajectory图6. 井眼轨迹三维图

Figure 7. Curvature changing with the depth of well图7. 曲率随井深变化

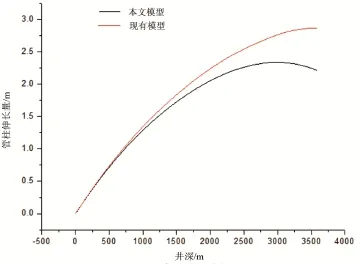
Figure 8. Pipe string elongation changing with the depth of well图8. 管柱伸长量随井深变化

Figure 9. Axial force changing with the depth of well图9. 轴向力随井深变化

Figure 10. The lateral force changing with the depth of well图10. 侧向力随井深变化

5. 结论

1) 在现有的管柱摩阻计算刚杆模型基础之上，通过修正管柱单元的浮力，得到了管柱真实轴向力的计算方法，建立了新的管柱摩阻计算模型。

2) 通过计算某一实际井在上提注水管柱时管柱的受力,发现管柱存在中性点，部分管柱存在受压的情况，这与管柱实际受力情况更加接近。

3) 通过有效轴向力和真实轴向力推导的两种管柱摩阻计算模型所计算的摩阻和大钩载荷基本一致，其误差是由管柱单元的附加轴向力计算不精确而导致。

References)

[1] Johansick, C.A. (1984) Torque and Drag in Directional Wells Prediction and Measurement. AIDC/SPE11380.

[2] Sheppard, M.C. (1987) Designing Well Paths to Reduce Drag and Torque. SPE15463.

[3] Maidla, E.E. and Wojtanowicz, A.K. (1987) Field Comparison of 2-D and 3-D Methods for the Borehole Friction Evaluation in Directional Wells. SPE16663.

[4] Ho, H.-S. (1988) An Improved Modeling Program for Computing the Torque and Drag in Directional Deep Wells. SPE18047.

[5] 张建群, 孙学增, 潘卫国. 定向井中摩擦阻力模式及其应用的初步研究[J]. 大庆石油学院学报, 1989, 4(13): 23-28.

[6] 韩志勇. 井眼内钻柱摩阻的三维两组模型的研究[J]. 石油大学学报, 1993, 17(7): 44-49.

[7] 李子丰, 刘希圣. 水平井钻柱稳态拉力-扭力矩模型及应用[J]. 石油钻探技术, 1992, 4(20): 1-6.

[8] 马善洲, 韩志勇. 水平井钻柱摩阻力和摩阻力矩的计算[J]. 石油大学学报, 1996, 20(6): 24-28.

[9] 眭满仓, 孟坤六. 水平井管柱下入摩阻分析及应用[J]. 石油机械, 1999, 21(2): 5-8.

[10] 高德利, 覃成锦, 李文勇. 南海西江大位移井摩阻和扭矩数值分析研究[J]. 石油钻采工艺, 2000, 23(5): 7-12.

[11] 秦永和, 付胜利, 高德利. 大位移井摩阻扭矩力学分析新模型[J]. 天然气工业, 2006, 26(11): 77-79.

[12] 檀朝东, 闫学峰, 杨喜柱, 等. 大位移水平井完井管柱力学分析研究[J]. 石油矿场机械, 2008, 37(2): 20-24.

[13] 宋执武, 高德利, 马建. 大位移井摩阻–扭矩预测计算模型[J]. 石油钻采工艺, 2006, 28(6): 1-3.

[14] 王志国, 俆壁华, 陈超, 等. 复杂井眼条件下扶正器对套管下入摩阻的影响研究[J]. 钻采工艺, 2014, 37(1): 37-30.

[15] 刘延强, 吕英民. 钻柱拖扭阻力的计算分析[J]. 石油学报, 1996, 17(3): 110-115.

[16] 申晓莉. 定向井管柱单元结构浮力计算公式修正[J]. 石油机械, 2014, 42(5): 77-83.

[17] Ho, H.-S. (1990) Method of P redicting the Torque and Drag in Directional Wells. United States Patent 4972703, 1990-11-27.

[18] 刘清友, 孟庆华, 庞东晓. 钻井系统动力学仿真研究及应用[M]. 北京: 科学出版社. 2009: 91-95.

Calculation and Application of Real Axial Force of Downhole Pipe String

Ding Feng1,2,3, Jie Wang1,2,3, Liqin Qian1,2,3, Qiaolei Sun1,2,3, Hong Zhang1,2,3, Yiliu Tu1,2,3
1School of Mechanical Engineering, Yangtze University, Jingzhou Hubei2Oil and Gas Drilling and Well Completion Tools Research Center, Jingzhou Hubei3Hubei Collaborative Innovation Center of Unconventional Oil and Gas (Yangtze University), Wuhan Hubei

The calculation precision of pipe string’s fraction was directly related to the quality of well completion. Domestic and foreign scholars have established a lot of models to calculate the friction of pipe string, of which the “rigid rod model” was more frequently used, but the static pressure without liquid at ends of micro-unit was not taken into account when the buoyancy of pipe string on the unit is calculated, thus the calculation of axial force was the effective axial force. For the pipe string unit that only side is contacted with liquid, if the displaced fluid gravity is used as its buoyancy, additional axial force would be generated at the ends of the unit, the real axial force of pipe string is calculated based on the study above, a new calculation formula is established for improving the accuracy of calculation of pipe string friction. To verify the accuracy of the model, the existing rigid rod model and the model established in this paper are used to solve the stress of water injection string when it is lifted in a actual well, and Matlab program is used to solve it. By comparing the results of the two models, the results of the model of this paper show that the pipe string exists neutral point, the pipe string above the neutral point is subjected to tension and the pipe string below the neutral point is subjected to pressure, this result is closer to the actual stress state of pipe string.

Rigid Model, Effective Axial Force, Real Axial Force, Additional Axial Force, Neutral Point

冯定(1963-)，男，教授，博士生导师，主要从事油气装备及井下工具的设计、诊断及动态仿真，方面的教学与研究工作。

Email: fend0861@163.com

2016年3月10日；录用日期：2016年4月15日；发布日期：2016年9月15日

文章引用: 冯定, 王杰, 钱利勤, 孙巧雷, 张红, 涂亿柳. 井下管柱的真实轴向力计算与应用[J]. 石油天然气学报, 2016, 38(3): 67-78. http://dx.doi.org/10.12677/jogt.2016.383027