裂缝性致密砂岩储层声波测井物理模型试验

龚 丹，章成广油气资源与勘探技术教育部重点实验室(长江大学)，湖北 武汉长江大学期刊社，湖北 荆州

裂缝性致密砂岩储层声波测井物理模型试验

龚 丹1,2，章成广1
1油气资源与勘探技术教育部重点实验室(长江大学)，湖北 武汉2长江大学期刊社，湖北 荆州

http://dx.doi.org/10.12677/jogt.2016.383024

Received: Apr. 12th, 2016; accepted: Jun. 11th, 2016; published: Sep. 15th, 2016

Copyright © 2016 by authors, Yangtze University and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

低孔、低渗致密砂岩油气藏等复杂油气藏是当前及今后相当长时间内油气勘探的主体。因此，低孔、低渗致密砂岩的精细评价成为测井专业的发展趋势和核心任务。为此，开展了裂缝性致密砂岩储层声波测井物理模型试验研究。该次研究包括模型井试验和小岩心试验两部分：模型井试验用100倍带光源读数显微镜(刻度1DIV/0.02 mm)来刻度裂缝宽度(100 µm～14 mm)，再用声波测井换能器来测量不同裂缝宽度时的波形；小岩心试验针对不同孔隙度(3.7%～7.5%)、不同裂缝宽度(30～500 µm)下，纵波、横波同一时刻的波峰幅度进行纵向对比，得到声波幅度的变化趋势。试验结果表明：随着裂缝宽度的增加，纵波和横波幅度都呈明显的衰减趋势；与纵波幅度的变化情况相比，横波的衰减情况更严重；裂缝宽度越大，纵波、横波衰减系数越大。综合物理模型试验测量结果及已研究的数值模拟计算结果认为，当裂缝宽度小于100 μm时，波形幅度随裂缝宽度的变化非常敏感，递减幅度非常快，不能定量确定裂缝宽度。

声波测井，裂缝性致密砂岩，物理模型，测井响应特征

1. 引言

近年来，中国油气探明储量构成及未来剩余油气资源预测研究表明，低孔、低渗致密砂岩油气藏等复杂油气藏是当前以及今后相当长时间内油气勘探开发的主体。因此，低孔、低渗致密砂岩的精细评价成为测井专业的发展趋势和核心任务。通过物理模型试验，对含有裂缝的致密储层的井孔声场进行研究，掌握裂缝对井内声场的影响规律，对于声波测井数据处理及解释具有的重要意义。

由于试验条件及技术的限制，国内外学者的研究相对较少。Hornby等[1]基于平板状裂缝模型，利用低频解析公式研究了斯通利波通过单一裂缝时的传播及反射特性。Tang等[2]-[8]对水平及垂直裂缝与斯通利波之间的响应关系进行了理论分析和试验研究。Chen [9] [10]在20世纪80年代在小模型井中对声波全波列进行过试验观测，后来又在小模型井中针对模拟的硬地层和软地层分别开展了多极子横波测井试验研究。Winkler等[11]在小模型井中观测了斯通利波衰减与裂缝渗透性的关系，并与理论数值分析结果作了对比。李长文等[12] [13]在人造砂岩模型井中进行过全波列观测试验和数据处理分析，以及储层渗透性变化及裂缝大小对声波波列及其频谱特征参数影响的研究。但是，上述试验研究的裂缝宽度几乎都停留在毫米级，对微米级裂缝宽度的试验研究很少。为此，笔者对致密砂岩中微米级的裂缝展开了声波物理模型试验研究，该次研究包括模型井和小岩心两部分。

2. 模型井试验

2.1. 模型井设计及裂缝刻度

该次试验模拟井外为无限大的硬地层，主要遵循以下几个设计原则：①模型参数(井径、声源主频)按一定比例与实际测井情况相类比；②制作的模型井能够与数值模型的计算结果进行对比，并保证模型介质的各向异性；③采用的模型井材料，其横波速度必须大于井液的纵波速度，以满足井外介质为硬地层的假设；④模型井尺寸必须足够大，能够忽略其边界效应，即经边界发射回来的波必须晚于有用信号的到达，模型的高度必须大于临界距离。在该次物理模型试验研究中，根据相似理论将井孔和换能器的尺寸缩小10倍、声源频率提高10倍的方法来模拟实际井中弹性波的传播。与声系尺寸相比，实际井的深度可以看作是无限的，井壁地层厚度也可视为无限的。

该次试验涉及到研究不同源距时的斯通利波波形变化，以及不同源距时斯通利波与裂缝的响应关系，因此需要改变声波测井声系的源距。试验声系采用一发一收，在试验过程中，需要给声系安装扶正器，以保证声系在井眼中时刻居中。

模型井井壁厚度的设计主要取决于声波探测深度的大小。在单极子声波测井中，纵波的探测深度与声系源距有关，当源距为3～4 in时，声波速度的探测深度约为10 cm左右。因此可以近似地认为，在井壁层厚度至少为15 cm的模型井中，在短源距的条件下能够测得斯通利波的传播速度。根据上述分析，设定模型井高为40 cm，直径为40 cm，井孔直径为25 mm，井壁厚18.75 cm。

将制作好的石英砂岩岩心放入实验室水槽中进行测量(图1，图2)。模型井的裂缝依靠人工控制，即将两块模型井的截面磨平、磨光滑，然后紧紧贴在一起，再用100倍带光源读数显微镜(刻度1DIV/0.02 mm)来刻度裂缝宽度(图3)。通过人工和机器调整裂缝宽度用以测量不同裂缝宽度时的波形。该次模型井试验中，最小裂缝宽度控制为100 μm。

Figure 1. Model wells in laboratory flume图1. 水槽中的模型井

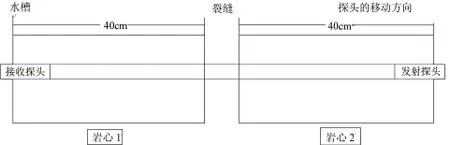
Figure 2. Schematic of model well for flume experimental图2. 模型井水槽试验示意图

Figure 3. The crack photographs of model well图3. 模型井的人工裂缝刻度

2.2. 试验结果与分析

图4、图5分别是砂岩模型井3号探头(频率50 kHz)变源距波形图和固定源距14 cm波形图，裂缝宽度300 μm。可以看出，当源距变长时，横波(S)、斯通利波(ST)波至时间变长、波形幅度变小；当声探头穿过裂缝时，横波、斯通利波波形幅度明显变小。其他探头(频率100、150 k Hz)所测波形图与3号探头所测波形图的规律一致。

3. 小岩心试验

3.1. 试验材料及裂缝刻度

试验所采用的天然岩心是取自新疆塔里木盆地大北克深地区各井中的岩心。选取孔隙度和渗透率相仿的两块岩心为一组，共5组10块，岩心长度采用游标卡尺直接测量。

该次试验主要是通过测量并记录模型在不同裂缝宽度时的波形，计算出纵波、横波的到达时间，通过记录同一时刻的纵波、横波的波峰幅度来研究纵波、横波幅度与裂缝宽度之间的关系。表1是5组岩心的实际测量长度及纵波、横波到达时间。

试验的难点在于需要将裂缝宽度控制到微米级，采用“人造缝技术”，即用岩心加持器将两块物性相同或相近的岩心夹在一起，中间夹塑料薄膜，通过加减塑料薄膜的厚度来精确控制裂缝宽度。图6是人造缝技术示意图。该次小岩心试验的裂缝宽度最小控制为30 μm。

3.2. 试验结果与分析

3.2.1. 时域图

该次试验使用TST3206动态测试分析仪获得全波列图形。图7是孔隙度3.7%岩心组的全波波形，可以看出，随着裂缝宽度的增加，纵波(P)、横波(S)幅度明显减小。其他4组岩心的波形特征与孔隙度3.7%岩心组的全波波形特征一致，都随裂缝宽度的增加，波形幅度有明显减小趋势。

3.2.2. 纵波幅度及衰减系数

图8是5组岩心纵波幅度与裂缝宽度关系汇总图，可以看出，裂缝宽度较小(裂缝宽度＜100 μm)时，波形幅度递减较快，波形衰减更明显；裂缝宽度较大时，波形幅度趋于平稳；孔隙度越大，纵波幅值越小。

图9是3组岩心纵波衰减系数与裂缝宽度关系汇总图，可以看出，孔隙度越大，纵波衰减系数越大。

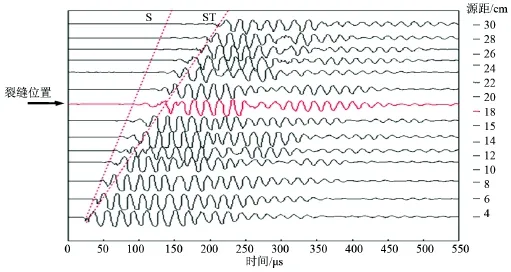
Figure 4. The simulation results of full waveform array received on the borehole axis of sandstone 3 probe with different sources图4. 砂岩3号探头变源距波形图

Figure 5. The simulation results of full waveform array received on the borehole axis of sandstone 3 probe, stationary sources is 14 cm图5. 砂岩3号探头固定源距14 cm波形图

Figure 6. Artificial crack technology图6. 人造缝技术

Figure 7. Array waveform of the core group what porosity is 3.7%图7. 孔隙度3.7%岩心组时域图

Figure 8. Summary relationship between longitudinal wave amplitude and crack width with different porosity of the five core group图8. 5组不同孔隙度岩心纵波幅度与裂缝宽度关系汇总图

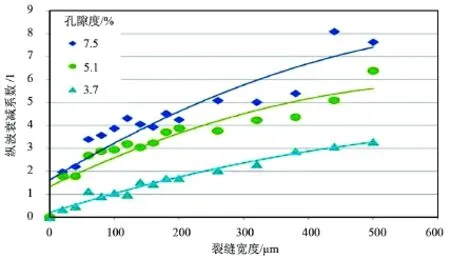
Figure 9. Summary relationship between longitudinal wave attenuation coefficient and crack width with different porosity of the three core group图9. 3组岩心纵波衰减系数与裂缝宽度关系汇总图

3.2.3. 横波幅度及衰减系数

图10是3组岩心横波幅度与裂缝宽度关系汇总图，可以看出，孔隙度越大，横波幅度越小；裂缝宽度较大时，波形幅度趋于平稳。与纵波幅度的变化趋势相比，横波的衰减更严重一些。

图11是3组岩心横波衰减系数与裂缝宽度关系汇总图，可以看出，孔隙度越大，横波衰减系数越大。

4. 数值模拟结果与物理模型结果对比

将变网格孔隙介质地层井孔声场数值模拟结果[14]与小岩心的实际测量结果(图12)进行对比，可以看出，孔隙介质数值模拟结果与小岩心的实际测量结果符合度较高。

Figure 10. Summary relationship between shear wave amplitude and crack width with different porosity of the three core group图10. 3组不同孔隙度岩心横波幅度与裂缝宽度关系汇总图

Figure 11. Summary relationship between shear wave attenuation coefficient and crack width with different porosity of the three core group图11. 3组岩心横波衰减系数与裂缝宽度关系汇总图

Table 1. Parameter list of five groups of core表1. 试验岩心纵波、横波到达时间

通过孔隙介质数值模拟研究结果[14]与小岩心试验模拟结果对比(图 13)可以看出，当裂缝宽度小于100 μm时，波形幅度随裂缝宽度的变化非常敏感，幅度减小非常快。综合分析认为，当裂缝宽度小于100 μm时，不能定量确定裂缝宽度。

5. 结论

通过物理模型手段，对微米级(模型井裂缝宽度最低100 μm，小岩心裂缝宽度最低30 μm)的单条水平裂缝进行了测试分析，得到了波形幅度、衰减系数与裂缝宽度、孔隙度的关系，取得了如下认识。

1) 当声探头穿过裂缝时，波形幅度变小；声探头穿过不同裂缝宽度的裂缝时，缝宽越大，波形幅度越小；当裂缝宽度较小时(裂缝宽度 ＜ 100 μm)，波形幅度递减很快，即波形幅度随裂缝宽度的变化非常敏感。

2) 裂缝宽度越大，纵波、横波幅度均减小，衰减系数均增大；在其他参数不变的情况下，孔隙度越大，纵波、横波衰减系数越大。

3) 根据数值模拟计算结果和物理模型试验结果综合认为，由于裂缝宽度小于100 μm时，波形幅度随裂缝宽度的变化非常敏感，幅度减小非常快。因此，当裂缝宽度小于100 μm时，不能定量确定裂缝宽度。

Figure 12. Contrast between the results of numerical simulation in pore medium and the results of experimental measurement图12. 孔隙介质数值模拟结果(孔隙度6%)与小岩心试验测量结果(孔隙度6.3%)对比图

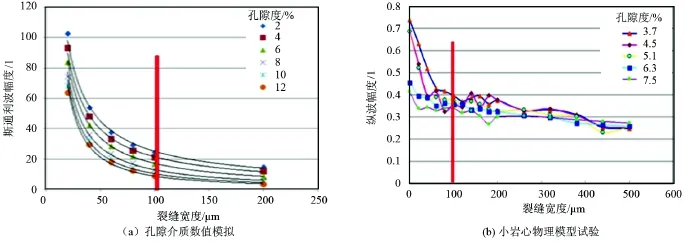
Figure 13. Relationship between sandstone crack width and wave amplitude图13. 砂岩裂缝宽度与波形幅度关系图

基金项目

国家科技重大专项(2011ZX0502-008)。

References)

[1] Hornby, B., Johnson, D. and Winkler, K. (1989) Fracture Evaluation Using Reflected Stoneley-Wave Arrivals. Geophysics, 54, 1274-1288. http://dx.doi.org/10.1190/1.1442587

[2] Tang, X.M. and Cheng, C.H. (1993) Borehole Stoneley Wave Propagation across Permeable Structures. Geophysical Prospecting, 41, 165-187. http://dx.doi.org/10.1111/j.1365-2478.1993.tb00864.x

[3] Tang, X.M. (1991) Dynamic Peameability and Borehole Stoneley Waves: A Simplified Biot-Rosenbaum Model. The Journal of the Acoustical Society of America, 90, 1632-1646. http://dx.doi.org/10.1121/1.401904

[4] Tang, X.M. and Cheng, C.H. (1996) Fast Inversion of Formation Permeability from Stoneley Wave Logs Using a Simplified Biot-Rosenbaum Model. Geophysics, 61, 639-645. http://dx.doi.org/10.1190/1.1443993

[5] Tang, X.M. (1991) Dynamic Peameability and Borehole Stoneley Waves: A Simplified Biot-Rosenbaum Model. The Journal of the Acoustical Society of America, 90, 1632-1646. http://dx.doi.org/10.1121/1.401904

[6] Tang, X.M. and Cheng, C.H. (1993) Borehole Stoneley Wave Propagation across Permeable Structures. Geophysical Prospecting, 41, 165-187. http://dx.doi.org/10.1111/j.1365-2478.1993.tb00864.x

[7] Tang, X.M. and Cheng, C.H. (1996) Fast Inversion of Formation Permeability from Stoneley Wave Logs Using a Simplified Biot-Rosenbaum Model. Geophysics, 61, 639-645. http://dx.doi.org/10.1190/1.1443993

[8] Tang, X.M. (1990) Acoustic Logging in Crackd and Porous Formations. Ph.D. Thesis, Massachusetts Institute of Technology, Boston.

[9] Chen, S.T. (1982) The Full Acoustic Wave Train in a Laboratory Model of a Borehole. Geophysics, 47, 1512-1520. http://dx.doi.org/10.1190/1.1441301

[10] Chen, S.T. (1989) Shear Wave Logging with Muhi-Pole Sources. Geophysics, 54, 590-597. http://dx.doi.org/10.1190/1.1442686

[11] Winkler, K.W. (1989) Permeability and Borehole Stoneley Waves: Comparison between Experiment and Theory. Geophysics, 54, 66-75. http://dx.doi.org/10.1190/1.1442578

[12] 李长文. 水平渗透性裂缝对并孔斯通利波传播的影响[J]. 测井技术, 1996, 20(3): 162-168.

[13] 余春昊, 李长文. 利用斯通利波信息进行裂缝评价[J]. 测井技术, 1998, 22(3): 273-277.

[14] 龚丹, 章成广. 裂缝性致密砂岩储层声波测井数值模型研究[J]. 石油天然气学报, 2016, 38(2): 29-35.

The Physical Model Experiment of Sonic Logging in Fractured Tight Sandstone Reservoirs

Dan Gong1,2, Chengguang Zhang1
1Key Laboratory of Exploration Technologies for Oil and Gas Resources (Yangtze University), Ministry of Education, Wuhan Hubei2Periodical Agency of Yangtze University, Jingzhou Hubei

Tight sandstone reservoir with low porosity and low permeability has been the major location for oil and gas exploration at present and in the years to come. Therefore, the fine evaluation of tight sandstone reservoirs with low porosity and low permeability was a development trend and core task for well logging. For this purpose, the research and experiment of sonic logging physical model were carried out in fractured tight sandstone reservoirs. The research included modeling wells and small core experiments. The modeling wells experiment was carried out by using 100 time light readout microscope (scale 1DIV/0.02 mm) to scale the fracture width (100 µm - 14 mm), and acoustic logging transducer was applied to measure the waveforms at different fracture widths. In the small core experiment, different porosities (3.7% - 7.5%) and different fissure widths (30 - 500 µm) were taken into consideration, the P-wave and S-wave amplitudes were longitudinally compared in the experiment at the same time and the variation trend of wave amplitude was obtained from the experiment. The experiment results showed that diminishing trend of P-wave and S-wave amplitude attenuation was more obvious with the increase of fracture width. Compared with the changes of the P-wave amplitude, attenuation of S-wave was more obvious. The greater the fracture width was, the larger the attenuation coefficient of P-wave and S-wave was. The results of physical model and numerical simulation show that waveform amplitude is very sensitive and diminishes rapidly with the change of fracture width when the fracture width is less than 100 μm. Therefore fracture width cannot be determined quantitatively.

Acoustic Logging, Fractured Tight Sandstone, Physical Model, Logging Response Characteristics

龚丹(1981-)，女，博士，讲师，主要从事石油天然气勘探的研究及编辑工作。

Email: 332486030@qq.com

2016年4月12日；录用日期：2016年6月11日；发布日期：2016年9月15日

文章引用: 龚丹, 章成广. 裂缝性致密砂岩储层声波测井物理模型试验[J]. 石油天然气学报, 2016, 38(3): 41-49.

http://dx.doi.org/10.12677/jogt.2016.383024