一道课本习题的“变脸”

□陈德前



一道课本习题的“变脸”

□陈德前

人教版八年级《数学》下册第69页第14题（以下简称“原题”）是：

如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F.求证：AE＝EF.（提示：取AB的中点G，连结EG）

根据题目中的提示，本题的证明并不困难，请同学们自己完成.这是一道知识内涵丰富，思想方法独特，具有较高的拓展价值的典型习题.以它为基础，可以演变出许多新颖的试题.

例1数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点.∠AEF＝90°，且EF交正方形外角∠DCG的平分线CF于点F，求证：AE＝EF.

经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM＝EC，易证△AME≌△ECF，所以AE＝EF.

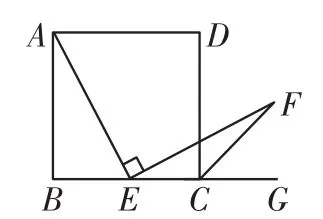
图1

在此基础上，同学们作了进一步的研究：

（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其他条件不变，那么结论“AE＝EF”仍然成立.你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由.

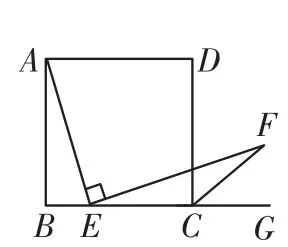
图2

图3

（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE＝EF”仍然成立.你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由.

分析：题目中给出的基础题就是上述原题，小明展示的解题思路具有一般性，是探索和证明后续问题的基础，即在∠BAE＝∠FEG的条件下，只要构造AM＝EC就可以得到∠AME＝∠ECF＝135°，进而有△AME≌△ECF，这样即可得到结论.

解：（1）正确.证明：在AB上取一点M，使AM=EC，连接ME，如图4，则BM＝BE.

∴∠BME＝45°，

∴∠AME＝135°.

∵CF是外角平分线，

∴∠DCF＝45°，

∴∠ECF＝135°，

∴∠AME＝∠ECF.

∵∠AEB＋∠BAE＝90°，

∠AEB＋∠CEF＝90°，

∴∠BAE＝∠CEF.

∴△AME≌△ECF（ASA），

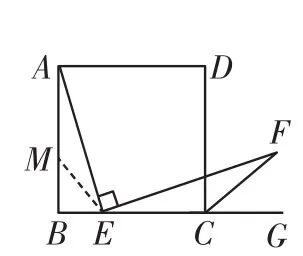
图4

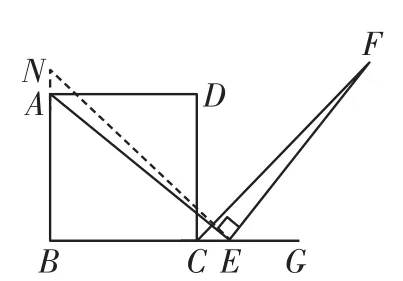
图5

∴AE＝EF.

（2）正确.证明：在BA的延长线上取一点N，使AN＝CE，连接NE，如图5，则BN＝BE.

∴∠N＝∠FCE＝45°.

∵四边形ABCD是正方形，

∴AD∥BE，

∴∠DAE＝∠BEA.

又∵∠NAD＝∠AEF＝90°，

∴∠NAE＝∠CEF.

∴△ANE≌△ECF（ASA），

∴AE＝EF.

例2如图6，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过E点作EF⊥AE交∠DCE的平分线于F点，试探究线段AE与EF的数量关系，并说明理由.

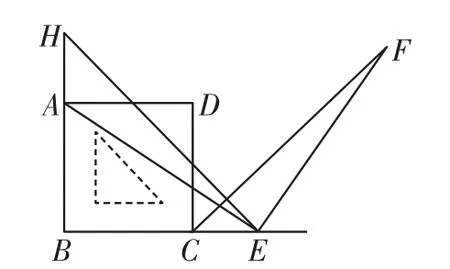
图6

分析：本题将原题中的条件“点E是边BC的中点”弱化为E为直线BC上的一点，但题目中增加了条件“一个含45°的三角板HBE”，可以得到HA＝CE，为解决问题提供了便利.

简证：由∠H＝∠FCE，AH＝CE，∠HAE＝∠CEF可证△HAE≌△CEF，从而得到AE＝EF.

例3（1）如图7，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点.若∠AMN＝90°，求证：AM＝MN.

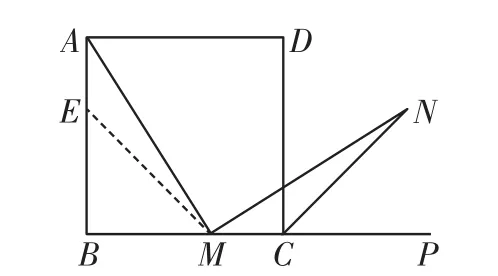
图7

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明.

证明：在边AB上截取AE＝MC，连接ME.在正方形ABCD中，∠B＝∠BCD＝90°，AB＝BC.

∴∠NMC＝180°－∠AMN－∠AMB

＝180°－∠B－∠AMB＝∠MAE.

（下面请你完成余下的证明过程）

（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图8），N是∠ACP的平分线上一点，则当∠AMN＝60°时，结论AM＝MN是否还成立？请说明理由.

图8

（3）若将（1）中的“正方形ABCD”改为“正n边形ABCD…X”，请你作出猜想：当∠AMN＝_______时，结论AM＝MN仍然成立.（直接写出答案，不需要证明）

分析：本题第（1）题给出了原题的解题思路，第（2）、（3）题将正方形变为正三角形、正n边形，结论仍然成立，其分析思考过程渗透了猜想、类比、归纳等数学思想方法.

（2）仍然成立.在边AB上截取AE＝MC，连接ME，如图8.

∵△ABC是等边三角形，

∴AB＝BC，∠B＝∠ACB＝60°，

∴∠ACP＝120°.

∵AE＝MC，∴BE＝BM，

∴△BEM是等边三角形，

∴∠BEM＝60°，

∴∠AEM＝120°.

∵CN平分∠ACP，

∴∠PCN＝60°，

∴∠MCN＝120°.

∵∠CMN＝180°－∠AMN－∠AMB

＝180°－∠B－∠AMB＝∠BAM，

∴△AEM≌△MCN，

∴AM＝MN.

许多中考题都是由课本习题演变而来的，所以我们要重视对课本习题的学习、研究、变化、引申，这样我们才能以不变应万变，提高我们的应变能力.