车道被占对道路通行能力影响的定量分析

袁则奕，朱家明

（1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

车道被占对道路通行能力影响的定量分析

袁则奕1，朱家明2*

（1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

针对车道被占对城市道路通行能力影响的问题，以差异检验、排队论、车流波动论为基础，求得了事故横断面实际通行能力的变化过程.利用队列分析模型，分析对占道不同的实际通行能力，建立基于车流波动理论的排队长度模型，求解出了排队长度与通行能力、持续时间、上游车流量的关系.

车道占用；通行能力；排队论；车流波动理论；SPSS

车道被占用是指因交通事故、路边停车、占道施工等因素，导致车道或道路横断面通行能力在单位时间内降低的现象.由于城市道路具有交通流密度大、连续性强等特点，一条车道被占用，也可能降低路段所有车道的通行能力，即使时间短，也可能引起车辆排队，出现交通阻塞.如处理不当，甚至出现区域性拥堵.车道被占用的情况种类繁多、复杂，正确估算车道被占用对城市道路通行能力的影响程度，将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据.

1 数据的获取与假设

1.1 数据获取

数据来源于2012全国大学生数学建模A题.

1.1.1 缺失数据的处理

对于所给视频帧数缺失导致数据统计结果，可以应用删除法、插补法，结合SPSS软件，利用插补法处理缺失值.

1.1.2 标准车当量数的计算

通行能力的求解是以要求的车辆数为标准车辆，将实际的各种车型按一定的折算系数［1］换算成某种标准车型的当量交通数.我国的标准车型为小客车，相关转换系数（见表1）.标准车当量数值为第i种车的折算系数，pi为第i种车的数目.

表1 标准车型转换系数Tab.1Standard model conversion factor

1.2 模型假设

为便于分析，提出以下假设：1）假设三个车道的车速相同，均为60 km/h；2）假设一辆标准车通过横断面的时间、换道的时间、等待的实际相同；3）假设上游路段交通需求量大于事发路段现有通行能力；4）假设整个路段为封闭系统，车流到达的规律不受外界影响.

2 事故处实际交通能力的变化过程

2.1 研究思路

根据视频一进行了车型数据的采集，并统一化为了标准车当量数，再求得理想通行状态下的通行能力，并进一步增加修正系数，建立实际通行能力评估模型.

2.2 研究方法

2.2.1 实际通行能力评估模型

2.2.1.1 数据采集

根据所给数据，求得每分钟的车型数目，并转换为了标准车当量数，限于篇幅只给出事故发生后前三分钟的车辆数目.

表2 事故发生后前三分钟的车辆数目Tab.2 The number of vehicles in the first three minutes after the accident

2.2.1.2 基本（理想）通行能力［2］

基本通行能力是指交通为理想状况时，单位时间内可能通过某一断面的当量小客车量最大值.理想的交通状况，即道路满足：车道宽度≤4.5m，侧向净宽≥1.75m，车辆的型号均为标准车型（小客车），驾驶员技术熟练，以相同的速度与车距，连续不断地向相同方向行驶.

在这种情况下，横断面的通行能力即最大车流量：

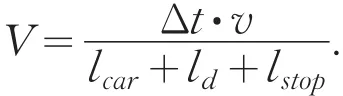
lcar为标准车型的平均长度，取4m；ld为车辆之间的车距，取5m；lstop为车辆之间的制动距离，取25m；Δt为单位时间，取为1h=3600s；v为车辆的平均速度，取

求得理想状况下的基本通行能力V理想=1764.7 pcu/h.

2.2.1.3 确定修正系数

影响通行能力的因素很多，选主要的影响因素进行修正：

交通条件：即标准车当量数的计算，将不同类型的车量数换算为标准车当量数，在模型的准备部分有详细解说.

道路条件：查阅相关文献［3］，得到车速修正系数fv为0.91；方向修正系数fd为0.94；车道宽度与侧向净宽修正系数fW=0.92；（4）驾驶员条件修正系数fp：一般在0.9～1.0范围内取值，取0.95；（5）横向干扰修正系数ff取 0.91；（6）大型车修正系数为大型车交通量所占百分比，EHV为大型车换算成标准小客车型的换算系数.结合模型准备的标准车当量数的计算，得到大型车修正系数随着时间变化的值（见表3）.

表3 不同时间的大型车修正系数Tab.3 Correction factor for large vehicle at different time

2.3 通行能力变化过程的分析

根据以上分析，得到实际通行能力公式：

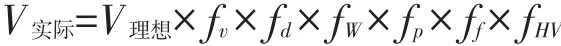
V理想为横断面的基本通行能力，fx为各项修正系数.

根据以上公式得到交通事故发生至撤离期间每分钟的实际通行能力数值的折线图（见图1）.

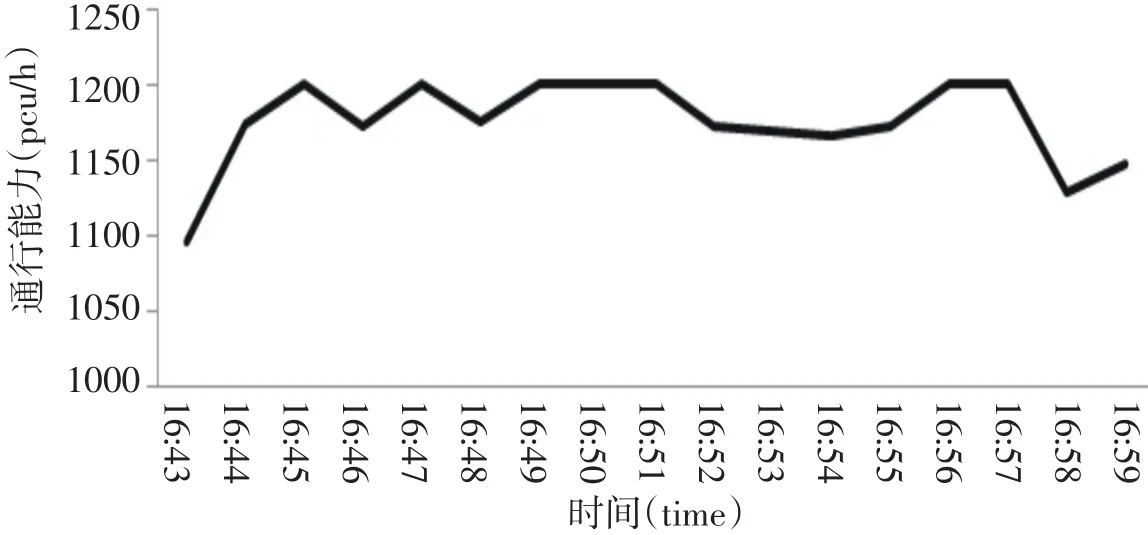
图1 每分钟实际通行能力变化图Fig.1 Actual traffic change per minute

交通事故发生至撤离期间，事故横断面的实际通行能力呈现波动的变化趋势，大车数目多的时段，V的值相应变低，这是由于体型较大的车换道也耗费更长时间；此外，交通灯的前半分钟为通行相位，后半分钟红灯阻行，导致了折线峰值的重复出现.

3 障碍车道差异对实际通行能力影响

3.1 研究思路

要分析同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异，首先可以在部分2的求解结果基础上利用SPSS进行正态检验，结合F检验与T检验对通行能力进行显著性差异分析，再建立基于排队论的单服务多队列分析模型，并判断不同车道障碍对实际通行能力的影响.

3.2 显著性差异分析［4］

正态性检验：利用SPSS对视频一与视频二的通行能力数据进行正态性检验，得到sig1=0.228，sig2=0.781，两组数据均符合正态分布.

方差齐性F检验在显著性水平α=0.05的条件下，F=0.159＜F表（16，27）=2.06，认为两组通行能力数据具有方差齐性.

显著性差异T检验：在显著性水平α=0.05的条件下，查阅t分布表，没有拒绝原假设，说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响无显著的差异.

出现上述结果的原因可能是由于车道1与车道3的通行能力差别不明显，建立基于排队论的单服务多队列模型进行深入的分析.

3.3 基于排队论的单服务多队列［5］模型

这是一个M/M/1排队问题，横断面的可通行路口认为是一个“服务台”，三条车道的车辆认为是三列排队的“顾客”.“服务台”一次只可服务一位“顾客”，其他队列的“顾客”进行队列的转换后，才可在“服务台”当列排队等候服务.

考虑到要分析车道不同对该横断面实际通行能力影响的差异，通过单样本的非参数检验，车辆的到达服从参数λ的负指数分布，车辆通行时间均服从参数μ的泊松分布.

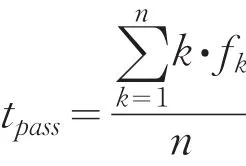
得到衡量两断口通行能力的平均服务率［6］辆/min）

3.4 差异分析

视频一占2、3车道，视频二占1、2车道，位于可通行车道的车辆通过端口前只经历排队，位于事故所占车道的车辆经历换道再排队的过程.

图2 车道1Fig.2Vehicle Lane 1

图3 车道2Fig.3Vehicle Lane 2

车道1的平均到达率λ≈3.9辆/s，车道2的λ2=8.18，车道3的λ3=6.5，可见车道2的总体车流量最多，车道1与车道3的通行能力差别不明显，解释了显著性差异不明显的原因.根据公式求出平均通过时间tpass≈5s，排队时间twait=8s，车道1的换道时间tchange=0s，车道2、3从车道i到允许通行的车道1需要进行i-1次换道，换道的时间tchange=（i-1）·2s，视频一的服务设备的利用率ρ≈0.85，这表明横断面路口有85%的时间是繁忙的，15%的时间为空闲的，而对于视频二的设备利用率ρ2≈0.79，这说明占据中内车道的实际通行能力要高于占据中外车道的实际通行能力.

做出占用不同车道时每分钟的通行能力折线图对模型加以验证.

分析得知发生车祸之后的1～3 min内，两视频的通行能力都处于较低的水平1100 pcu/h，由于另一条未发生车祸的车道仍能通行，随着交通的疏导，致使车祸后1～3 min时段的通行能力有所上升，上升至1200 pcu/h之后，由于红绿灯通行相位的间隔性，导致通行能力呈现以分钟为周期的波动趋势，视频二的平均通行能力低于视频一的，这说明事故后，可通行的道路越靠近内车道3，总体通行能力越高.

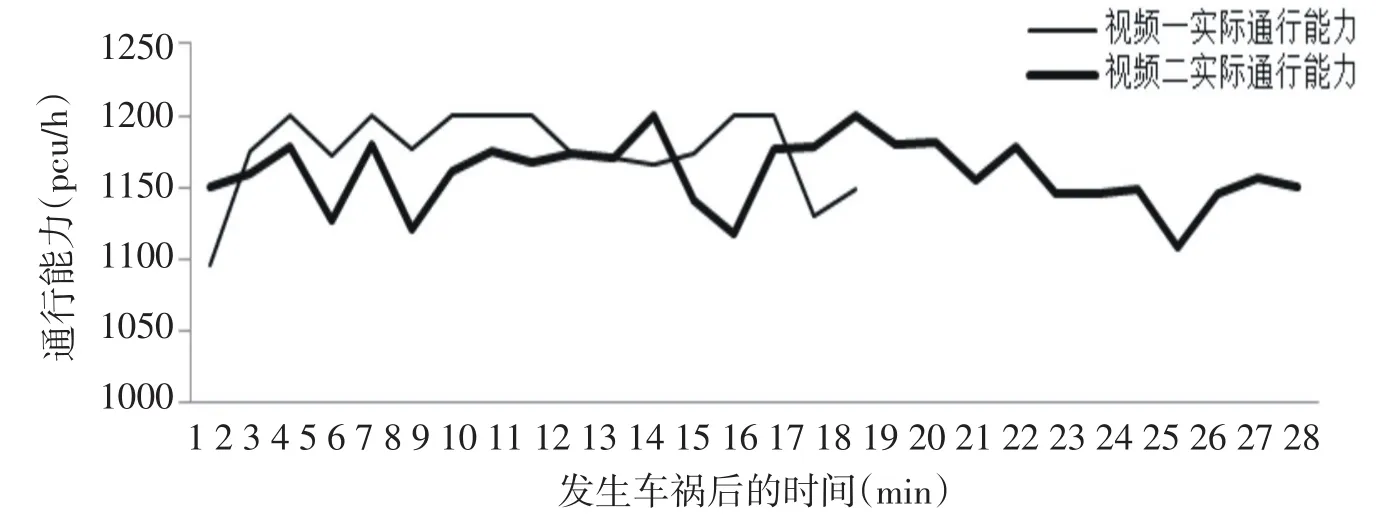
图4 占用不同车道时每分钟的通行能力折线图Fig.4 Traffic capacity of taking different lanes per minute

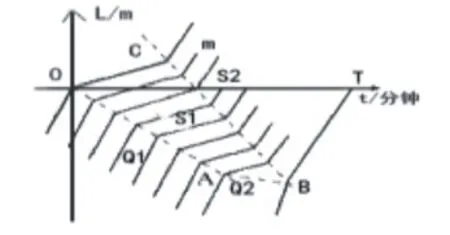
图5 车流波动传播图Fig.5 Traffic flow fluctuation

4 车辆排队长度研究

4.1 研究思路

车流波动理论：车流中不同密度的分界面向车队后部传播的现象，称为车流波动.根据假设3，上游交通需求量大于事发路段现有通行能力，车流会在横断面形成队列，形成集结波，波面以一定的速度向车队的后方传播；事故解除后，集结波继续向车队后方传播，在车队的前方同时形成消散波，排队车辆恢复为具有适当密度的车流，当消散波的速度大于集结波的速度时排队消散完成.

4.2 研究方法

由车流波动理论［7］可知，波速的公式：

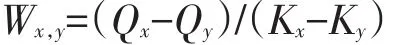
其中Wx，y为集散波的波速，km/h；Qx，Qy分别为前后两种车流状态的流量，辆/h；Kx，Ky为前后两种车流状态的密度，辆/km.

根据交通流理论［8］和Green-shields的速度-密度线性关系模型，有Q=v×K，其中Q为交通量，v为行车速度，K为车流密度；v=vf（1-K/Kj）其中vf为畅行速度，Kj为阻塞密度，所以波速与密度的关系为Wx，y=vf［1-（Kx-Ky）/Kj］.

图5中每条曲线表示一辆车运行的时间-空间轨迹.横轴表示时间，纵轴表示与事故点的相对位置，原点O表示事故发生点，纵轴的负半轴表示事故点的上游，正半轴表示事故点的下游.虚线OA，OB表示集结波，CB表示消散波，其斜率的绝对值表示波速，斜率的正负号表示波传播的方向.两波相遇的时间为T，当集结波与消散波在T＞0的时间内有交点时，表示车队可以在有限的时间内消散.假设两波相遇前该路段需求量始终为Q1，与相交处表示排队向上延伸到达的最远处，设两波相遇的时间为T，集结波的速度为W1，消散波的速度为Wx，根据两波相遇时传播距离一样有下列关系：

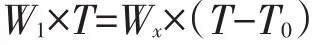
其中

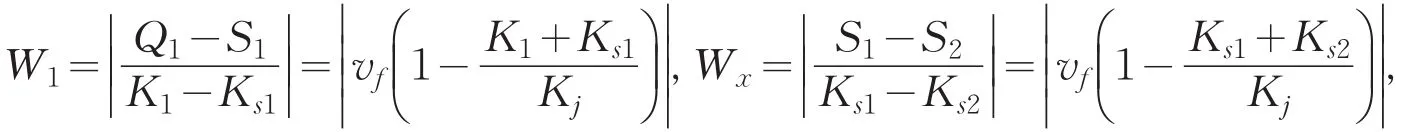
则：

若T＞T1（T1为Q1车流量持续的时间），则说明在车队消散之前该路段上游需求量发生了变化，需求量变为Q2，相应的密度变为K2，所以得到等式

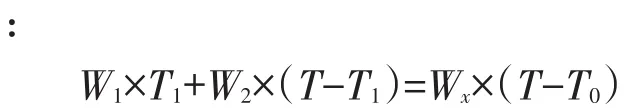
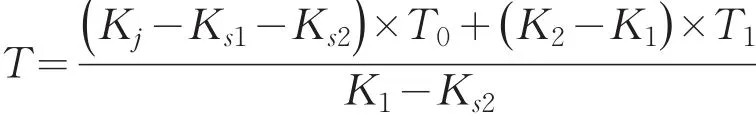
对于此问，上游车流量是随时间发生变化的周期函数，即每分钟发生一次变化，从Q1变为Q2，再变为Q1，再变为Q2，依次循环.所以，可得下列等式：

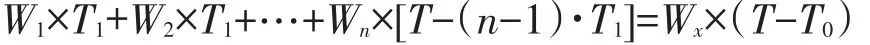
其中T1=1min，以此求出排队时间T的表达式，得到关于事故横断面实际通行能力、事故持续时间、路段上游车流量三者间的排队长度公式：

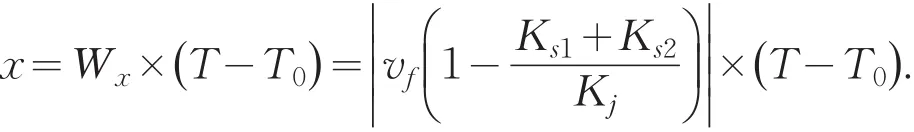
4.3 结果分析

通过对求解阻塞密度、估算车速和车流密度，求得排队的持续时间：

因此根据排队长度

将代入，求得排队长度x表达式为

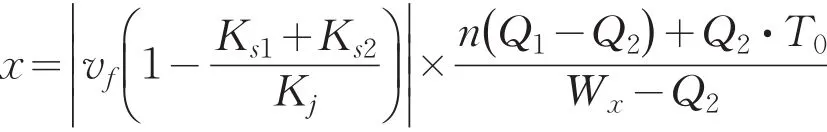
至此，求出了排队长度x和事故横断面实际通行能力S1、事故持续时间T0、路段上游车流量Q之间的关系，分析可知，当实际通行能力S1增大时，排队长度x会变短，一般事故疏散前的实际通行能力小于事故疏散后的实际通行能力，当事故疏散之后，排队的车辆可以通过被拥堵的车道，交通状况恢复正常，排队长度降低；当事故持续时间T0增大时，排队长度x会变长；当上游车流量Q1和Q2的差值增大，即在绿灯时来自上游路口直行的车辆增多时，排队长度会变长.

［1］王进.车辆折算系数研究［J］.土木工程学报，2014，37（12）：98-99.

［2］李磊.城市道路车辆缩减区通行能力研究［J］.公路与汽运，2013（2）：30-33.

［3］刘磊.基于元胞自动机的高速公路作业区通行能力分析研究［D］.西安：长安大学，2012.

［4］盛骤.概率论与数理统计［M］.北京：高等教育出版社，2008.

［5］保利勇，赵东风，洪伟.多队列单服务台式限定服务排队系统性分析［J］.云南大学学报：自然科学版，1992，31（s1）：1-4.

［6］周强.同时具有可变输入率与可变服务率以及一类差错服务率可变的M/M/1排队模型［D］.重庆：重庆师范大学，2010.

［7］张恺鸽，许妮妮，杨希媚，等.交通事故对城市道路通行能力的影响——基于车流波动理论分析［J］.科技创新与生产力，2014（4）：102-106.

［8］姚荣涵，王殿海，曲昭伟.基于二流理论的拥挤交通流当量排队长度模型［J］.东南大学学报：自然科学版，2007，37（3）：521-526.

责任编辑：刘 红

Quantitative Analysis of the Impact of Lane Occupancy on Urban Traffic Capacity

YUAN Zeyi1，ZHU Jiaming2*

（1.School of Finance，Anhui University of Finance and Economics，Bengbu 233030，China 2.School of Statistics and Applied Mathematics，Anhui University of Finance and Economics，Bengbu 233030，China）

Focusing on the impact of lane occupancy on urban traffic capacity，we obtained the change process of the actual capacity of the accident cross section relying on differences testing，queuing theory and traffic flow wave theory.By means ofqueue analysis model，we analyzed the actual traffic capacity of the lanes.And then by establishinga queue length model depending on the traffic flow wave theory，we found the relation between queuing length，the traffic capacity，duration and upstream traffic.

Lane occupancy；traffic capacity；queuing theory；traffic flow wave theory；SPSS

U 491.31

A

1674-4942（2016）02-0137-06

2016-02-27

国家自然科学基金资助项目（11301001）；安徽财经大学教研项目（acjyzd201429）

*通讯作者