含氟聚合物/多壁碳纳米管复合材料的导热性能

林聪妹, 曾贵玉, 刘佳辉, 黄 忠, 巩飞艳, 张建虎, 刘世俊

(中国工程物理研究院化工材料研究所, 四川 绵阳 621999)

1 引 言

作为一种新型的准一维功能材料,碳纳米管具有高模量、高强度、良好的导电性和导热性,在复合材料、电化学器材、储氢材料、场发射装置、传感器、催化剂载体等方面获得广泛应用[1-2]。碳纳米管是迄今为止人们所知最好的导热材料。根据理论预测,多壁碳纳米管的导热系数可达3000 W·m-1·K-1[3],而单壁碳纳米管的导热系数更高,可达6000 W·m-1·K-1[4]。试验结果显示,添加少量的碳纳米管可以显著改善有机流体或者高聚物的导热性[5-6]。Biercuk等人[5]制备了单壁碳纳米管/环氧树脂复合材料,40 K和室温下导热性能比环氧树脂分别提高70%和125%。Hong等人[7]通过添加1.0%单壁碳纳米管和4.0%多壁碳纳米管将聚甲基丙烯酸甲酯(PMMA)的导热系数从0.24 W·m-1·K-1分别提高至2.43 W·m-1·K-1和3.44 W·m-1·K-1。

复合材料的导热系数不仅取决于材料本身导热性质,还与界面热阻有重要关系。由于碳纳米管与高聚物基体间的界面热阻大[8],即使添加导热系数很高的碳纳米管,复合材料的导热系数增幅也较小。Cahill团队[9]首次测试了碳纳米管悬浮液中碳纳米管与基体界面处的界面热阻,指出较大的界面热阻限制了复合材料的热传导。据报道,碳纳米管与基体界面处的界面热阻为8 3× 10-8m2·K·W-1[10]。可见,界面热阻对碳纳米管复合材料的导热系数具有显著的影响。因此,降低碳纳米管与高聚物间界面热阻成为复合材料领域的研究热点。赵瑾朝等[11]采用二氧化硅(SiO2)包覆层作为过渡层,降低聚氨酯(PU)与MWCNTs间的模量失配,减少声子的界面散射,提高PU/SiO2-MWCNT复合材料的导热性能。当SiO2-MWCNTs的质量分数为0.5%和1.0%时,PU/SiO2-MWCNT复合材料的热导率比纯PU分别提高了53.7%和63.8%。

近年来,随着纳米科学技术的发展,碳纳米管在含能材料领域的研究和应用引起了国内外学者的广泛关注[12]。但是关于碳纳米管对粘结剂体系导热性能影响的研究报道较少。本研究采用密炼混合方式制备了含氟聚合物F2314/多壁碳纳米管(MWCNTs)复合材料,利用激光脉冲法测试了复合材料的导热行为,考察了碳纳米管含量和温度对复合材料导热行为的影响,分析了F2314/MWCNTs复合材料的导热机理,应用有效介质方法修正模型从理论上计算了复合材料的有效导热系数,并模拟了复合材料的导热行为,以期为碳纳米管导热复合材料在PBX中的应用提供理论和试验依据。

2 试验部分

2.1 原料

氟聚物F2314(氯含量为26.3%,重均分子量为2.74×105g·mol-1,多分散系数为3.37)由中昊晨光化工研究院生产; 多壁碳纳米管(MWCNTs),外径约为20 nm,长度约为5 μm,深圳纳米港公司提供。

2.2 F2314/MWCNTs复合材料的制备

将质量比为2∶98、5∶95、10∶90、20∶80和30∶70的MWCNTs与F2314进行密炼混合,然后微注塑制成Φ12.7 mm×2 mm试样,用于热物理性能测试,分别记作FC-1、FC-2、FC-3、FC-4和FC-5,其成型密度分别为2.023,2.028,2.031,2.038 g·cm-3和2.049 g·cm-3。

2.3 微观形貌结构分析

利用CamScan Apollo 300型扫描电子显微镜(SEM)观察F2314/MWCNTs复合材料的形貌结构,试验电压为10 kV,高真空模式。

2.4 热物理性能测试

参照GJB772A-1997(406.2)《比热容、导热率和热扩散率激光脉冲法》,采用耐驰公司LFA 447NanoflashTM型闪光导热仪,在温度范围为30～70 ℃的条件下,对微注塑成型、尺寸为Ф12.7 mm×2 mm的F2314/MWCNTs复合材料进行导热系数测试。

3 结果与讨论

3.1 微观形貌结构分析

图1是不同MWCNTs含量的F2314/MWCNTs复合材料的SEM图。从图1可以看出,MWCNTs加入量为2%时,MWCNTs在基体中分散较为均匀,只存在少量的团聚体。当MWCNTs含量达到5%以上,F2314基体中存在明显的MWCNTs团聚现象。

a. FC-1 b. FC-2 c. FC-3

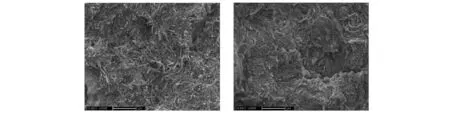
d. FC-4 e. FC-5

图1 F2314/MWCNTs复合材料的微观形貌结构

Fig.1 The micro morphology structure of F2314/MWCNTs composites

3.2 碳纳米管含量对F2314/MWCNTs复合材料导热性能的影响

图2是30 ℃下不同MWCNTs含量F2314/MWCNTs复合材料的导热系数。从图2可以看出,随着碳纳米管含量增加,F2314/MWCNTs复合材料的导热系数明显提高。30 ℃时,纯F2314的导热系数为0.146 W·m-1·K-1。在F2314中加入质量分数为2%的MWCNTs,复合材料FC-1的导热系数提高至0.183 W·m-1·K-1。当碳纳米管质量分数提高至30%时,FC-5的导热系数为0.647 W·m-1·K-1,比纯F2314导热系数提高3.43倍。MWCNTs在F2314基体中随机分布且相互搭接,由于MWCNTs具有较大的长径比,可以形成骨架结构,并在热流方向上形成导热链。随着MWCNTs含量增加,搭接点数目增加,MWCNTs在基体中形成互穿网络结构,从而提高了复合材料的导热性能。但是,与纯F2314相比,F2314/MWCNTs复合材料的导热系数增幅不大。这与文献报道的其它聚合物/碳纳米管体系的情况一致[7]。这主要是因为碳纳米管与F2314基体间的界面热阻大,热量在传递过程中急剧下降,因此添加高导热的MWCNTs后, F2314/MWCNTs复合材料的导热系数不是很高,远小于F2314和MWCNTs导热系数的线性加和(FC-1、FC-2、FC-3、FC-4和FC-5复合材料的线性加和值分别为54.14,135.44,272.23,550.02,833.81 W·m-1·K-1)。

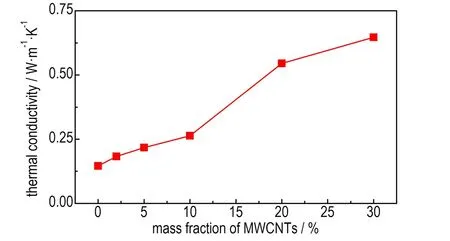
图2 30 ℃下F2314/MWCNTs复合材料的导热系数与MWCNTs含量的关系

Fig.2 A plot of thermal conductivity of F2314/MWCNTs composites at 30 ℃ vs. MWCNTs content

3.3 温度对F2314/MWCNTs复合材料导热性能的影响

图3是F2314/MWCNTs复合材料的导热系数随温度的变化曲线。从图3可以看出,F2314/MWCNTs复合材料的导热系数随温度的变化呈现相同的规律,即导热系数先随着温度升高而增大,然后达到最大值,接着逐渐下降。F2314/MWCNTs复合材料的导热性能对温度的依赖性主要与F2314的相态转变密切相关。导热系数的最大值出现在50 ℃附近,对应于F2314/MWCNTs复合材料的玻璃化转变温度(～48 ℃)[13]。在其它导热粒子填充复合材料的导热系数与温度关系研究中也发现了类似的现象。例如,Agarwal等[14]制备了纤维/苯酚甲醛复合材料,发现复合材料的导热系数在玻璃化转变温度时达到最大值或者峰值。当温度低于玻璃化转变温度时(<50 ℃),随着温度升高,聚合物分子链逐渐伸展,导致声子平均自由程增加,因此材料的热阻降低,热导率提高。当温度高于F2314/MWCNTs复合材料的玻璃化转变温度时(>50 ℃),随着温度升高,分子链段运动产生的微孔数量和尺寸增大,导致复合材料导热系数随温度升高而降低[14]。

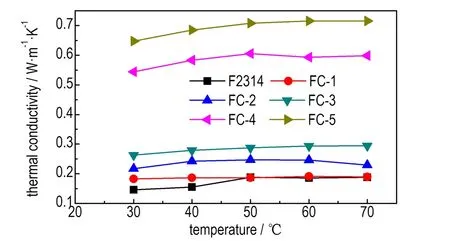
图3 F2314/MWCNTs复合材料的导热系数与温度的关系图

Fig.3 A plot of thermal conductivity of F2314/MWCNTs composites vs temperature

3.4 F2314/多壁碳纳米管复合材料的导热模型

当碳纳米管含量很低(f<0.02)时,Maxwell-Garnett型有效介质方法(EMA)[15]可以用于计算碳纳米管复合材料的有效导热系数。在碳纳米管复合材料中,碳纳米管的导热系数远高于高聚物基体的导热系数,且碳纳米管的长径比很大。根据有效介质方法,当碳纳米管随机分散在基体中时,碳纳米管复合材料的有效导热系数为[10]:

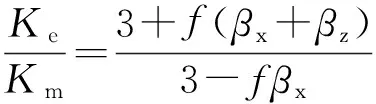
(1)

式中,Ke为碳纳米管复合材料的有效导热系数,W·m-1·K-1;Km为高聚物基体的导热系数,W·m-1·K-1;f为碳纳米管的体积分数,参数βx和βz可以用下式计算[10]:

(2)

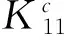
(3)

式中,Kc为碳纳米管的导热系数,W·m-1·K-1;d和L分别为碳纳米管的直径和长度,m;aK为Kapitza半径,m。通过高聚物基体的导热系数和界面热阻可以计算得到aK[10]:

aK=RKKm

(4)

式中,RK为界面热阻,又称为Kapitza热阻,m2·K·W-1; 与界面处的热流和温度梯度有关[10]:

Q≈ΔT/RK

(5)

式中,Q为界面处热流,W·m-2; ΔT为界面处温度梯度,K。

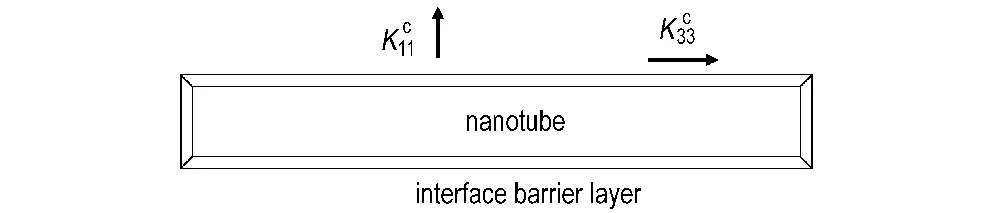
图4 复合材料晶胞的示意图[10]

Fig.4 Schematic illustration of a composite unit cell

式(1)为碳纳米管复合材料导热系数的EMA计算公式。该公式考虑了碳纳米管直径、长径比和体积分数、界面热阻、导热系数比Kc/Km对碳纳米管复合材料有效导热系数的影响。采用EMA公式可以计算得到不同碳纳米管含量的F2314/MWCNTs复合材料有效导热系数Ke,结果见表1。从表1可以看出,EMA公式计算得到的有效导热系数Ke的理论值比试验值略大。这一方面是因为EMA公式主要适用于碳纳米管含量为非常少(f<0.02)的复合材料。另一方面,碳纳米管之间存在较强的范德华引力,并且碳纳米管具有巨大的比表面积和很高的长径比,在加工过程中碳纳米管容易团聚、难以分散。

表1 30 ℃下不同含量碳纳米管的F2314/MWCNTs复合材料的导热系数

Table 1 The thermal conductivity of F2314/MWCNTs composites with different MWCNTs content at 30 ℃

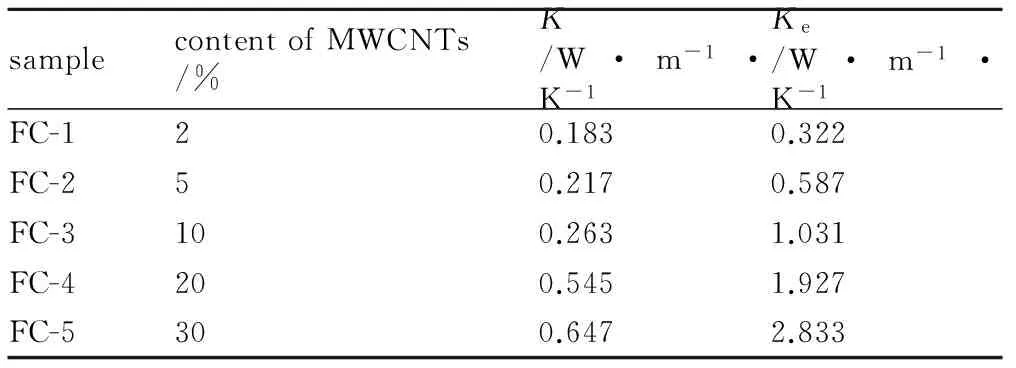
samplecontentofMWCNTs/%K/W·m-1·K-1Ke/W·m-1·K-1FC-120.1830.322FC-250.2170.587FC-3100.2631.031FC-4200.5451.927FC-5300.6472.833

Note:Kis thermal conductivity by test,Keis effective thermal conductivity with interface thermal resistance.

图5揭示了F2314/MWCNTs复合材料有效导热系数Ke的理论计算值与试验值的关系。从图5可以看出,有效导热系数Ke的理论计算值与试验值之间呈线性关系。

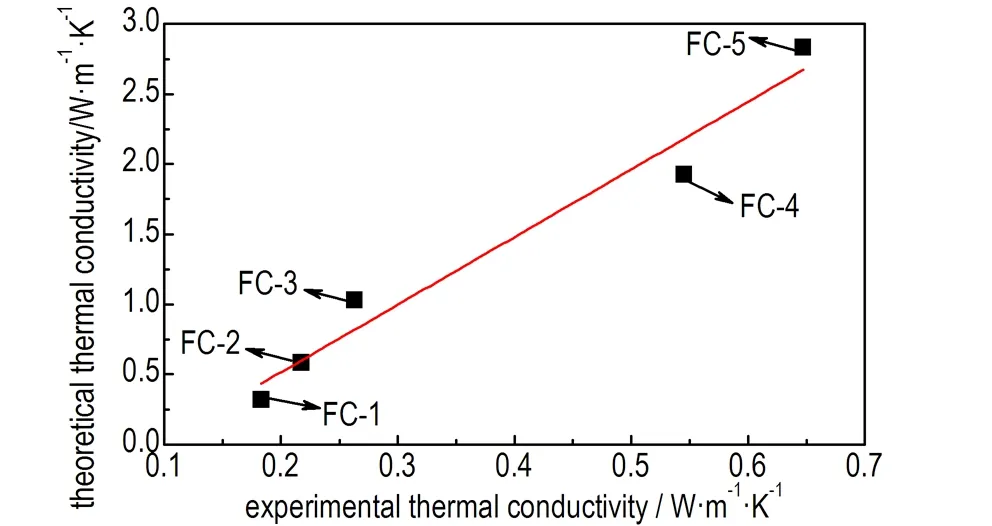
图5 30 ℃下F2314/MWCNTs复合材料的导热系数的计算值与试验值的关系

Fig.5 Relationship between the calculated values and experimental ones of thermal conductivity for F2314/MWCNTs composites at 30 ℃

因此,为了更加准确地描述高碳纳米管含量的F2314/MWCNTs复合材料有效导热系数Ke,引入两个常数C1和C2修正EMA公式:

(6)

通过图5有效导热系数Ke的理论计算值与试验值的线性拟合可以得到C1和C2分别为4.8241和0.6383。EMA修正公式的计算结果与试验值基本吻合,如图6所示。可见,采用EMA修正模型可以较好地模拟F2314/MWCNTs复合材料的导热系数测试结果,理论模型与试验结果的相对误差为0.95%～16.7%。

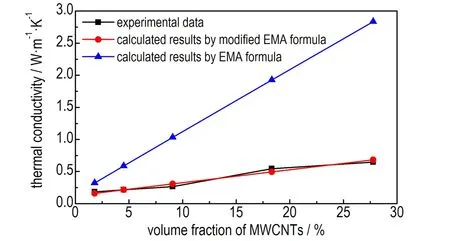
图6 30 ℃下F2314/MWCNTs复合材料导热系数的EMA公式及其修正公式的计算值与实验值的对比

Fig.6 Comparison of the calculated values by EMA formula and its modified formula and the experimental ones of thermal conductivity for F2314/MWCNTs composites at 30 ℃

4 结 论

(1)F2314/MWCNTs复合材料的导热系数随MWCNTs含量的增加而增大,当MWCNTs质量含量从2%提高至30%时,复合材料的导热系数从0.183 W·m-1·K-1增加到0.647 W·m-1·K-1。

(2)F2314/MWCNTs复合材料的导热系数对温度的依赖性与F2314的相态转变有关。当温度低于玻璃化转变温度时,复合材料导热系数随温度升高而增大。当温度高于玻璃化转变温度时,复合材料导热系数随温度升高而降低。

(3)有效介质方法(EMA)修正模型可以较好地模拟F2314/MWCNTs复合材料的导热性能,理论模型与试验结果的相对误差为0.95%～16.7%。

参考文献:

[1] Iijima A. Helical microtubes of graphitic carbon[J].Nature, 1991, 354(6348): 56-58.

[2] 陈利魁, 盛涤伦, 杨斌, 等. 碳纳米管及碳黑对BNCP感度性能的影响[J]. 含能材料, 2013, 21(1): 35-38.

CHEN Li-kui, SHENG Di-lun, YANG Bin, et al. Effects ofcarbon nanotubes and carbon black on sensitivity performances of BNCP[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2013, 21(1): 35-38.

[3] Kim P, Shi L, Majumdar A, et al. Thermal transport measurements of individual multiwalled nanotubes[J].PhysicalReviewLetters, 2001, 87(21): 215502.

[4] Berber S, Kwon Y, Tomanek D. Unusually high thermal conductivity of carbon nanotubes[J].PhysicalReviewLetters, 2000, 84(20): 4613-4616.

[5] Biercuk M J, Llaguno M C, Radosavljevic M, et al. Carbon nanotube composites for thermal management[J].AppliedPhysicsLetters, 2002, 80(15): 2767-2770.

[6] Choi S U S, Zhang Z G, Yu W, et al. Anomalous thermal conductivity enhancement in nanotube suspensions[J].AppliedPhysicsLetters, 2001, 79(14): 2252-2254.

[7] Hong W T, Tai N H. Investigations on the thermal conductivity of composites reinforced with carbon nanotubes[J].Diamond&RelatedMaterials, 2008, 17(7-10): 1577-1581.

[8] Nan C W, Birringer R. Determining the Kapitza resistance and the thermal conductivity of polycrystals: A simple model[J].PhysicalReviewB(CondensedMatterandMaterialsPhysics), 1998, 57(14): 8264-8268.

[9] Huxtable S, Cahill D G, Shenogin S, et al. Interfacial heat flow in carbon nanotube suspensions[J].NatureMaterials, 2003, 2(11): 731-734.

[10] Nan C W, Liu G, Lin Y H, et al. Interface effect on thermal conductivity of carbon nanotube composites[J].AppliedPhysicsLetters, 2004, 85(16): 3549-3551.

[11] 赵瑾朝, 杜飞鹏, 崔伟, 等. 聚氨酯/二氧化硅包覆多壁碳纳米管复合材料的导热与电绝缘性能[J]. 高分子材料科学与工程, 2012, 28(3): 104-106.

ZHAO Jin-chao, DU Fei-peng, CUI Wei, et al. Thermal conductivity and electrical insulation of polyurethane/silica-coated multi-walled carbon nanotube composites[J].PolymerMaterialsScienceandEngineering, 2012, 28(3): 104-106.

[12] 曾贵玉,林聪妹,周建华, 等. 碳纳米管对HMX热分解行为的影响[J]. 火炸药学报, 2012, 35(6): 55-57.

ZENG Gui-yu, LIN Cong-mei,ZHOU Jian-hua, et al. Influences of carbon nanotubes on the thermal decomposition behavior of HMX[J].ChineseJournalofExplosives&Propellants, 2012, 35(6): 55-57.

[13] 林聪妹, 刘佳辉, 刘世俊, 等. DMA方法研究多壁碳纳米管/F2314复合材料的粘弹性能[J]. 含能材料, 2015, 23(2): 140-145.

LIN Cong-mei, LIU Jia-hui, LIU Shi-jun, et al.Characterization viscoelastic properties of multi-walled carbon nanotubes/F2314 composites using DMA method[J].ChineseJournalofEnergeticMaterials(HannengCailiao) , 2015, 23(2): 140-145.

[14] Agarwal R, Saxena N S, Sharma K B, et al. Temperature dependence of effective thermal conductivity and thermal diffusivity of treated and untreated polymer composites[J].JournalofAppliedPolymerScience, 2003, 89(6): 1708-1714.

[15] Nan C W, Shi Z, Lin Y. A simple model for thermal conductivity of carbon nanotube-based composites[J].ChemicalPhysicsLetters, 2003, 375(5-6): 666-669.