一种新的炸药感度判据: 键非键耦合分子刚柔度
2016-05-11谭碧生李金山龙新平
谭碧生, 黄 明, 李金山, 龙新平,2
(1. 中国工程物理研究院化工材料研究所, 四川 绵阳 621999; 2. 中国工程物理研究院, 四川 绵阳 621999)
1 引 言
炸药研究工作者对感度的认识是与时俱进的。在炸药的研究和实践中,一些学者提出了炸药感度的判据[1-2],如最易跃迁法(能隙最小)[3]、最小键级法[4]、最弱X—NO2(XC, N, O)键离解能[5-6]、硝基电荷法[7]等,这些方法对我们理解炸药的感度起到了很重要的作用。随着炸药研究科学技术水平的发展,人们对感度的认识会越来越深刻,越来越接近炸药感度的本质。虽然影响炸药的感度因素很多,需要从多尺度的角度出发来认识,但影响炸药感度的因素不外乎三种: 分子、晶体和环境[8]。环境的因素主要是考虑炸药在不同的刺激下的反应,在力、热、声、光、电、磁等各种物理刺激下,它们表现出不同的反应性,可以将它们分为热感度、光感度、静电火花感度、撞击感度、冲击波感度和摩擦感度等[9]。如在研究炸药的热感度时,炸药的熔点、比热,以及导热、传热等性能会受到关注,导热、传热性能优良,则其感度会较低; 研究静电火花感度时,炸药的介电极化性能可能起着关键作用,如果在电场作用下其易被极化,则其感度会较高[10-11]; 研究其光感度时(如激光感度),应该考虑光子与电子的耦合,当光的波长(或频率)和强度与炸药分子的某些易导致分解的振动模式相匹配,甚至激光的相位与炸药分子的相位相匹配时,容易导致引发反应而表现出高的感度[12-14]; 研究炸药的撞击感度、冲击波感度和摩擦感度等机械感度时,其能量形式被认为是声子作用,声子的频率一般低于200 cm-1,而导致炸药分子分解的相关的振动的频率一般都在1000 cm-1以上,因此,必须考虑声子与电子的耦合,才能将其能量转移到炸药分子上,有学者提出了“多声子泵浦”理论 (multiphonon up-pumping)[15-16]。因此,不管是何种形态的炸药,在何种刺激下,其引发反应最终都会落在其分子结构上。
在实际操作中,炸药的机械感度可能更多地受到关注,因此本文中选择了11种典型单质炸药,研究撞击感度与其分子结构的关系。比较了这些炸药的特性落高与几种判据之间的相关性,包括最弱键的键级判据、最易跃迁判据、硝基电荷判据、最弱键的离解能判据。作者在近几年的工作中[17-29],总结出了评价炸药分子感度的“键非键耦合分子刚柔度法”,即,从炸药分子的电子离域性的大小来衡量分子的“刚”与“柔”,分子越“刚”,其感度越高,分子越“柔”,其感度越低。本文中对此方法的内涵予以了描述。
将炸药分子的刚柔度加入感度评价体系,重新对几种感度判据进行了比较,发现它们与感度的相关性的差异较大,其中与分子刚柔度相关的判据具有最好的相关性。前四种主要从分子的局部(硝基)来判断感度,这对X—NO2作为引发键的炸药分子是有效的,而“键非键耦合分子刚柔度法”则从分子的整体稳定性来判断,尤其是对于分子骨架断裂引发反应更为有效。对于那些不含硝基的炸药,如BTF(苯并三氧化呋咱)、全氮化合物以及含硼硅等杂原子的炸药,前面四种方法已经不适用。在撞击、冲击以及摩擦等外界机械力的作用下,炸药分子本身的变形而引起的张力的改变也是最显著的,以TNAZ的晶体为例,模拟在5 GPa(以此压力代表高压作用下的一种情形) 的静水压下,以上五种感度参数的变化,说明了这一点。
如果综合考虑炸药的整体和局部,即将这些感度参数综合考虑,建立感度的多参数模型,可以大大提高感度与分子结构的相关性。在本文结果与讨论的最后一部分,用遗传函数近似方法建立了感度与这些判据之间的联系,可以获得理想的预测结果。
与分子刚柔度相关的张力能既是一个感度判据指标,同时也是高能化合物储能的一种重要方式。以高能化合物CL-20、八硝基立方烷(ONC)和全氮化合物N8为例,本理论计算发现,张力能对其生成焓和爆热的贡献很大。
物理学上对硬度的定义: 物体抵抗外来的机械作用下发生塑性变形的难易程度,晶体的硬度是由它们的化学键决定的。对于同一种晶体,不同的晶面的硬度因其原子密度的不同而有差别。化学上的硬度的定义: 电负性差驱动着电子从电负性低的原子向电负性高的原子的流动,两个原子的硬度则对抗这种移动。电子在体系中易流动,则认为其分子结构“柔”,反之,则“刚”。 为此,本文提出了以电子的流动难易为基础的“键非键耦合分子刚柔度法”。
为了描述分子结构“柔”与“刚”,我们建立了基于等键和超等键设计的体系稳定化能“共振能”,以及去稳定化能“(环、网、笼)张力能”。共振能越负,分子越“柔”,其结构越稳定,炸药的感度则可能更低; 反之,张力能越正,分子越“刚”,其结构越不稳定,炸药的感度则可能更高。
张力能的产生,主要来源于两个方面。一方面,是由于在成键过程中成键的角度远离了中心原子杂化的自然轨道的角度而产生的张力,叫小角张力[30],可以从键的角度予以描述: 即键的伸缩、角的面内弯曲和面外弯曲、二面角扭曲可以产生张力; 另一方面,在高氮化合物或全氮化合物中,由于相邻氮原子上的孤电子对之间的相互排斥而产生的张力,叫非键相互作用张力[30],可以从非键相互作用进行描述: 主要包含相邻与邻近的原子和基团之间的范德华力和静电作用力,包含排斥和吸引。分子的张力能是两种作用,即键与非键作用耦合的结果。张力能是一个目前还不能实验确定的量,只能用理论研究方法,加上一些经验校正,如将椅式环己烷(环状)的张力能和金刚烷(笼状)的张力能最小作为参照。张力能其数值越正,张力能越大,结构越不稳定。因此,张力能是从环的稳定性角度出发评价化合物稳定性的特征指标,同时也是反应化合物储能的重要参数。
张力能究竟是一种物理能还是化学能的问题,引起人们的思考。从小角张力到非键相互作用看,这是由于力、力矩以及吸引和排斥产生,应为物理能; 但其表现为开环或开笼会释放出额外的这部分能量来看,似应为与化学键相关的化学能。
理论上采用等键反应设计[31-34]量化分子的刚柔度。根据等键反应方程(1)~(16)对一些典型炸药的刚柔度进行了理论分析,选择的炸药包含了芳香苯环、杂环、苯环与杂环互联及稠合结构、刚性杂环、笼型氮杂结构以及笼型全氮结构,具有一定的普遍意义。理论计算中,等键反应中所有的分子结构都采用杂化密度泛函B3LYP/6-31g(d,p)[35-36]来优化,用微扰理论MP2/6-311g(d,p)[37]计算单点能,由Gaussian 09[38]程序执行。利用公式(i)计算共振能(或张力能)[22]。

(i)
式中,ES为张力能(数值>0);E0i,ZPEi为分别为等键反应式中反应物(R)i组分的0 K时的总能量和零点振动能;E0j,ZPEj为分别为等键反应式中生成物(P)的0 K时的总能量和零点振动能;ni和nj分别为等键反应式中反应物和生产物的系数。共振能(<0)的计算也采用相同的方法。
下面对TNB、TNT、PCTA (2-苦基-1,2,3-三唑)、NPCTA (4-硝基-2-苦基-1,2,3-三唑)、LLM-105(2,6-二氨基-3,5-二硝基吡啶-1-氧化物)、DNBF(4,6-二硝基苯并呋咱)、DADNBF(5,7-二氨基-4,6-二硝基苯并呋咱)、TNAZ、RDX、K6、CL-20、ONC、N8(cube)、C6H6、N6、N6O3等化合物进行了等键反应设计,依照等键反应方程和公式计算它们的的刚柔度(共振能或张力能)。等键反应(1)~ (16)中由MP2/6-311g(d,p)计算的各种分子在0K下的能量以及零点能结果见表1,由公式(i)计算的各种炸药的共振能和张力能以及分子刚柔度结果见表2。虽然这些反应涉及离域键和定域键的转变,既有张力的变化,也有离域程度的变化,这些变化都包含在反应能量中。本文中没有明确区分这些变化,粗略地将负值认定为共振能,正值认定为张力能。

显然,TNB、TNT、PCTA (2-picryl-1,2,3-triazole)、NPCTA(4-nitro-2-picryl-1,2,3-triazole)、LLM-105、DNBF(4,6-dinitrobenzofuroxan)、DADNBF(5,7-diamino-4,6-dinitrobenzofuroxan)都是柔性化合物,TNAZ、RDX、K6、CL-20、ONC、N8(cube) 都是刚性化合物。苯是典型的芳香性分子,其共振能为-180.6 kJ·mol-1,其等电子体N6(见表2)似应为柔性结构,如果也能稳定存在或顺利实验合成,可能是一种理想的含能材料。计算结果表明,N6有较大的张力能(123.6 kJ·mol-1),不难理解,N6为什么至今难以实验合成[39]。如果将部分N6氧化(氧配位)成N6O3(见表2),则其张力能显著降低,甚至转化为共振能(-61.8 kJ·mol-1),这为全氮化合物的合成和稳定化提供了一条新的途径。
不能忽视的是,张力能是炸药分子的一种重要储能方式,张力能越大,其爆热、爆速或爆压可能越高。在表3中,以笼型的CL-20及其线型异构体为例,计算(MP2/6-311 g(d,p))其生成焓,与基团贡献法结果相比,发现线型异构体的基团贡献值[40-41](383.80 kJ·mol-1)与MP2(388.81 kJ·mol-1)计算值十分接近,而笼型异构体的基团贡献值加上笼张力能(372.7 kJ·mol-1),相对偏差达-46.2%,经热相关校正后,结果才能相比(相对偏差变为5.7%)。这也说明,张力能是生成焓的重要组成部分,或者说是炸药分子的一种重要储能方式。从表2 还可知,ONC 、N8(cube)等分子的张力能很大,如ONC分解产生CO2和N2,释放3475 kJ·mol-1的热量,其中包含张力能979.1 kJ·mol-1[42]。有趣的是,硝基立方烷可能是一类潜在的抗癌药物(抗癌炸弹),其药理竟然是利用立方烷释放出的张力能摧毁癌细胞[43]。
表1 根据等键反应(1)~ (16),在MP2/6-311g(d,p) 水平上计算的各种分子在0K下的总能量(E0)以及零点振动能(ZPE)
Table 1 The total energies(E0) at 0K and zero point vibrational energies (ZPE)of all kinds of molecules calculated at the level of MP2/6-311g(d,p) in terms of isodesmic reactions (1)~ (16)

compoundE0/hartreeZPE/hartreecompoundE0/hartreeZPE/hartreecompoundE0/hartreeZPE/hartreeTNB-843.8473440.107761-79.5708570.074935-247.8149590.100859TNT-883.0410140.135681-95.5833700.063593-526.9543700.109035PCTA-1084.2887440.146861-111.5836870.053304-338.8546690.095416NPCTA-1288.3695880.149074-131.4092060.039888-134.7861180.092992LLM-105-857.2847540.119276-360.8386570.111438-150.8108150.082326DNBF-897.8085010.101029-400.0338610.139456-224.7366850.061892DADNBF-1008.2818220.135893-416.0735870.128649-190.0127160.110311TNAZ-785.008240.106971-188.7746540.085839-156.7403150.108251RDX-895.4281560.142819-205.9628300.098116-220.7776040.060692K6-969.3086050.122560-392.8676770.088551-295.7816500.064656ONC-1941.2784380.149903-376.8586240.099287-221.9731240.087116CL-20-1787.32320020.220294-303.0167070.118921-231.5778420.100617N6-327.5339590.022129-448.1071190.102844-186.5755650.056507N6O3-552.6229310.039537-322.8333610.105016-436.4168090.034355
表2 根据等键反应(1)~ (16) 按照各种炸药的共振能(ER)和张力能(ES)所确定的刚柔度
Table 2 Rigid or flexible, determined according to resonance energies(ER) and strain energies (ES) of all kinds of explosives based on isodesmic reactions (1)~ (16)

compoundER/kJ·mol-1ES/kJ·mol-1“rigid”or“flexible”TNB-120.0-flexibleTNT-116.2-flexiblePCTA-169.1-flexibleNPCTA-138.4-flexibleLLM-105-103.8-flexibleDNBF-36.4-flexibleDADNBF-44.3-flexibleBenzene-180.6-flexibleN6O3-61.85-flexibleTNAZ-152.7rigidRDX-155.5rigidK6-275.2rigidCL-20-372.7rigidN6-123.6rigidONC-979.1rigidN8(cube)-895.3rigid
3 对几种感度判据的评价
最易跃迁法中的能隙(Eg)、硝基电荷法的QNO2、最弱键级法中BO及X—NO2最弱X—NO2(XN或O)键的离解能都在B3LYP/6-31g(d,p)的水平上进行计算,共振能或张力能的计算在前面进行了说明。计算结果见表4。表4可见,炸药分子的张力能越大,其感度可能越高。
(ii)
式中,Ωx,y,两数组的相关系数; CovX,Y,两数组的协方差;σx,σy分别为x和y数组的标准偏差。
共振能(或张力能)的相关系数最高,或者说与分子的刚柔度相关性最高。以TNAZ为例,模拟研究其晶体[45]中TNAZ在0 GPa 和5 GPa静水压作用下的上述参数的变化,结果见表5。
结果表明,在外界机械力的作用下,其能隙变窄,硝基电荷变负,键级减小,张力能显著增加。这进一步说明了TNAZ分子的刚度显著增加了,这预示着可能开环反应优先了。
图1~图5列出了11种典型炸药的特性落高与不同的判据之间的关系及其相关性。可以看出,虽然像硝基电荷以及分子的刚柔度等判据与其特性落高之间的相关性较高,但还是不够理想(图1~图5,线性相关系数为分别为0.5570,0.7260,0.6595,0.1927,0.7641),如果将这些判据组合起来,有可能获得满意的结果(图6,线性相关系数为0.9996)。
遗传算法(GA)[46-47],按照类似活的有机体的遗传(heredity)、突变(mutation)、自然选择(selection)和杂交(crossover)等的自然进化(natural evolution)方式编制的能够解决复杂的优化问题的计算机程序。
表3 按照基团贡献法(GAV)和MP2/6-311g(d,p) 法计算的CL-20及其线型异构体的气相生成焓的比较
Table 3 Comparison of gaseous enthalpies of formation of CL-20 and its linear isomer calculated according to groups additivity values′method (GAV) and MP2/6-311g(d,p) method
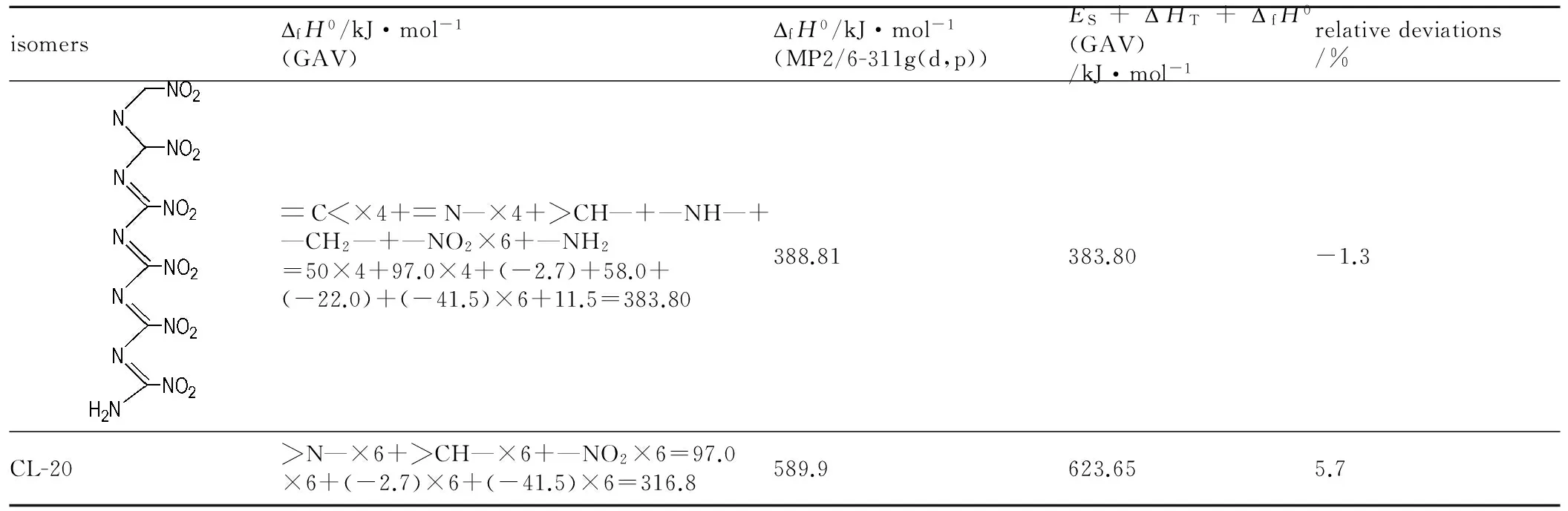
isomersDfH0/kJ·mol-1(GAV)DfH0/kJ·mol-1(MP2/6-311g(d,p))ES+DHT+DfH0(GAV)/kJ·mol-1relativedeviations/%C×4+N—×4+CH—+—NH—+—CH2—+—NO2×6+—NH2=50×4+97.0×4+(-2.7)+58.0+(-22.0)+(-41.5)×6+11.5=383.80388.81383.80-1.3CL-20N—×6+CH—×6+—NO2×6=97.0×6+(-2.7)×6+(-41.5)×6=316.8589.9623.655.7
Note: 623.65 is the calculated value obtained byES+HT+GAV method.
表4 典型炸药的特性落高及5种感度判据的结果

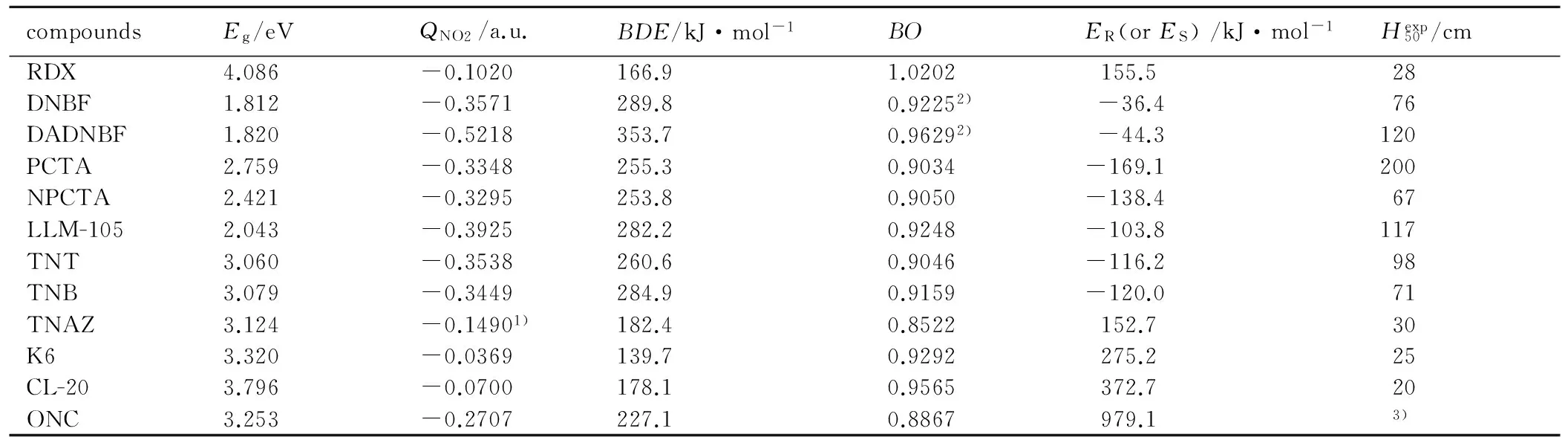
compoundsEg/eVQNO2/a.u.BDE/kJ·mol-1BOER(orES)/kJ·mol-1Hexp50/cmRDX4.086-0.1020166.91.0202155.528DNBF1.812-0.3571289.80.92252)-36.476DADNBF1.820-0.5218353.70.96292)-44.3120PCTA2.759-0.3348255.30.9034-169.1200NPCTA2.421-0.3295253.80.9050-138.467LLM-1052.043-0.3925282.20.9248-103.8117TNT3.060-0.3538260.60.9046-116.298TNB3.079-0.3449284.90.9159-120.071TNAZ3.124-0.14901)182.40.8522152.730K63.320-0.0369139.70.9292275.225CL-203.796-0.0700178.10.9565372.720ONC3.253-0.2707227.10.8867979.13)

表5 模拟TNAZ晶体在0 GPa和5 GPa静水压作用下的几种判据的变化值
Table 5 Changes of several criteria of modeling the TNAZ crystal under the hydrostatic pressure of 0 and 5 GPa

p/GPaEg/eVQNO2/a.u.BOER(orES)/kJ·mol-103.124-0.14900.8522152.752.022-0.20370.37488077.8relativedeviation/%-35.336.7-56.05190.0







图3 11种炸药的X—NO2(XN or O)键离解能与值之间的关系
Fig.3 Relationship between bond dissociation energies of X—NO2(XN or O) andvalues for 11 explosives



GA是模拟自然界生物进化过程的高度并行、随机和自适应的全局随机优化算法,是一种进化算法。它借助生物界自然选择和进化的规律,根据“优胜劣汰”和“适者生存”的原则,对自然界中生物群体由低级到高级、简单到复杂的生物进化过程进行模拟[48],借助复制、交换、突变等算子的操作,使目标函数值较优的变量被保留,而较差的变量被淘汰,随着不断的遗传迭代,最终使所要解决的问题从初始解逐渐逼近最优解[49]。计算的结果如下:

(iii)










compoundsHexp50/cmHcal50/cmRDX 28.0 26.8DNBF 76.0 75.8DADNBF 120.0 120.1PCTA 200.0 200.0NPCTA 67.0 66.3LLM-105 117.0 115.8TNT 98.0 99.2TNB 71.0 71.6TNAZ 30.0 30.4K6 25.0 26.8CL-20 20.0 19.1
由表6及图6可见,预测值与实验值非常吻合。一方面,说明此法预测能力强; 另一方面,说明采用多参数预测感度比单一参数具有更高的可靠性。此模型虽还未用更多的测试集进行修正,但是它已经为我们开辟了感度预测的一条新途径,随着测试集的逐步完善,预测方程可以得到更好的修正,预测的可靠性会更高。
4 结 论
对几种炸药感度判据,包括最易跃迁法(能隙)、最小键级、最弱键离解能、硝基电荷等几种方法进行了重新计算和评述,提出了基于分炸药子整体稳定性的“键非键耦合分子刚柔度法”的感度衡量方法。以11种典型炸药为例,包括RDX、DNBF、DADNBF、PCTA、NPCTA、LLM-105、TNT、TNB、TNAZ、K6和CL-20,比较了它们感度及其判据之间的相关性,结果表明,其高低顺序为: 分子刚柔度法>硝基电荷法>键离解能法>最易跃迁法。模拟TNAZ晶体也发现,在机械力作用下,分子的刚柔度表现得最显著。采用遗传函数近似的方法将几种判据组合,虽然失去了原来判据的物理意义,但能够显著提高其预测能力。张力能,包括环、网和笼张力能,是炸药分子中键非键耦合的一种炸药的能量形式,它不仅能够用于衡量炸药的感度,尤其是不含硝基炸药的感度,同时还能用来量度炸药的储能水平,通过对CL-20、ONC、N8等化合物的分析,发现张力能在其能量释放中扮演了相当重要的角色。在设计新型炸药分子时,必须充分考虑张力能的作用,根据不同的需求,如主炸药、起爆药、传爆药的具体要求,设计出合适的炸药分子。因此,分子刚柔度的思想对新型炸药的设计和评价具有重要意义。
致谢: 感谢中国工程物理研究院仿真中心对部分理论计算的支持。
参考文献:
[1] 肖继军, 李金山. 单体炸药撞击感度的理论判别——从热力学判据到动力学判据[J]. 含能材料, 2002, 10(4): 178-181.
XIAO Ji-jun, LI Jin-shan. The theoretical criteria of impact sensitivity of explosive compounds[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2002, 10(4): 178-181.
[2] 胡庆贤. 炸药感度评价方法的探讨[J]. 含能材料, 2000, 8(3): 127-129.
HU Qing-xian. The exploration of the evaluations of impact sensitivity of explosives[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2000, 8(3): 127-129.
[3] 宋华菊. 炸药感度的量子化学研究[D]. 南京: 南京理工大学[D]. 2004.
SONG Hua-ju. Quantum chemistry of impact sensitivity of explosives [D],Nanjing: Nanjing University of Science and technology[D]. 2004.
[4] 肖鹤鸣. 硝基化合物的分子轨道理论[M]. 北京: 国防工业出版社,1993: 365.
XIAO He-ming. Theory of molecular orbitals of nitro compounds [M].Beijing: China National Industry Press, 1993: 365.
[5] Politzer P, Murray J S. Relationships between dissociation energies and electrostatic potentials of C-NO2bonds: applications to impact sensitivities[J].JMolStruct, 1996, 376(1): 419-424.
[6] Rice B M, Sahu S, Owens F J. Density functional calculations of bond dissociation energies for NO2scission in some nitroaromatic molecules[J].JMolStruct(TheoChem), 2002, 583(5): 69-72.
[7] Zhang C, Shu Y, Huang Y. Investigation of correlation between impact sensitivities and nitro group charges in nitro compounds[J].JPhysChemB, 2005, 109(18): 8978-8982.
[8] Sharma J, Bread B C, Chaykovsky. Coorelation of impact sensitivity with electronic levels and structure of molecules[J].JPhysChem, 1991, 95(3): 1209-1213.
[9] Zeman S. Sensitivities of high energy compounds[J].StructBond, 2007, 125: 195-271.
[10] Maycock J N, Grabenstein D E. Piezoelectricity in secondary explosives[J].Science, 1966, 152(3721): 508-509.
[11] Raha K, Chhabra J S. Static charge development on explosives[J].DefSciJ, 1991, 41: 21-25.
[12] Wakeham G P, Chung D D, Nelson K A. Femtosecond time-resolved spectroscopy of energetic materials [J].ThermochimicaActa, 2002, 384: 7-21.
[13] Aluker E D, Krechetov A G, Mitrofanov A Y, Zverev A S, Kuklja M M. Understanding limits of the thermal mechanism of laser initiation of energetic materials [J].JPhysChemC, 2012, 116(46): 24482-24486.
[14] Gordon R J, Zhu L. Coherent control of chemical reactions [J].AccChemRes, 1999, 32(12): 1007-1016.
[15] Pkoff A T, Fayer M D, Dlott D D. Chemical reaction initiation and hot-spot formation in shocked energetic molecular materials[J].JPhysChem, 1993, 97: 1901-1913.
[16] Dlott D D, Fayer M D. Shocked molecular solids: vibrational up pumping, defect hot spot formation, and the onset of chemistry[J].JChemPhys, 1990, 92(6): 3798-812.
[17] Tan B, Long X, Peng R, et al. Two important factors influencing shock sensitivity of nitro compounds: Bond Dissociation Energy of X—NO2(XC, N, O) and Mulliken Charges of Nitro Group[J].JHazardMater, 2010, 183(1-3): 908-912.
[18] Tan B, Long X, Peng R,et al. Theoretical investigation of an energetic fullerene derivative[J].JComputChem, 2010, 31(12): 2233-2237.
[19] Tan B, Long X, Peng R, et al. Molecular design and properties prediction of cyclotetramethylene tetranitramine (HMX) derivatives with amido groups[J].JStructChem, 2010, 51(4): 616-621.
[20] Tan B, Long X, Peng R, et al. The Study on the aromaticity of fullerenes and their holmium endohedral compounds[J].JMolMod, 2011, 17(2): 275-279.
[21] Tan B, Long X, Peng R, et al. An important factor in relation to shock-induced chemistry: resonance energy[J].JMolMod, 2012, 18(2): 583-589.
[22] Tan B, Long X, Peng R, Jet al. On the shock sensitivity of explosive compounds with small scale gap test[J].JPhysChemA, 2011, 115(38): 10610-10616.
[23] 谭碧生, 龙新平, 彭汝芳, 等. 从共振能的角度研究四种苦基三唑衍生物的撞击感度[J]. 西南科技大学学报, 2011, 26(3): 1-5.
TAN Bi-sheng, LONG Xin-ping, PENG Ru-fang, et al. Studies of the impact sensitivity of four picryl-triazole explosives from the perspective of resonance energy[J].TheJournalofSouth-WestUniversityofScienceandTechnology, 2011, 26(3): 1-5.
[24] Tan B, Huang M, Long X, et al. Insight into shock-induced chemical reaction from the perspective of ring strain and rotation of chemical bonds[J].JMolMod, 2012, 18(12): 5127-5132.
[25] Tan B, Huang M, Long X, Li J. Theoretical investigation of several 1,2,3,4-tetrazine-based high-energy compounds[J].PropellantsExplosPyrotech, 2013, 38(3): 372-378.
[26] Tan B, Huang M, Long X, et al. Computational screening of several silicon-based high-energy hexanitrohexaazaisowurtzitane-like derivatives[J].JFluorChem, 2014, 158: 29-37.
[27] Tan B, Huang M, Long X, et al. Insight into a series of cage-like nitrogen oxides[J].Polyhedron, 2014, 79: 124-128.
[28] Tan B, Huang H, Huang M, et al. From planes to cluster: the design of polynitrogen molecules[J].IntJQuantumChem, 2015, 115(2): 84-89.
[29] Huang M, Tan B. Some strategies on the stabilization of explosives[J].ChinJEnergMater, 2014, 22(2): 134-135.
[30] Smith M B, March J. March′s advanced organic chemistry, reaction, mechanism, and structure[M]. 5thed, John Wiley & Sons, 2011.
[31] Wiberg K B. The concept of strain in organic chemistry[J].AngewChemIntEdEngl, 1986, 25(4): 312-322.
[32] Wheeler S E, Houk K N, Schleyer P R, et al. A hierarchy of homodesmotic reactions for thermochemistry[J].JAmChemSoc, 2009, 131(7): 2547-2560.
[33] Gimarc B M, Zhao M. Strain and resonance energies in main-group homoatomic rings and clusters[J].CoordChemRev, 1997, 158: 385-412.
[34] Bach R D, Dmitrenko O. The effect of substitutents on the strain energies of small ring compounds[J].JOrgChem, 2002, 67(8): 2588-2599.
[35] Becke A D. Density functional thermochemistry. III. The role of exact exchange[J].JChemPhys, 1993, 98(7): 5648-5652.
[36] Lee C, Yang W, Parr R G. Development of the colle-salvetti correction-energy formula into a functional of the electron density[J].PhysRevB, 1988, 37: 785-789.
[37] Moller C, Plesset M S. Note on an approximation treatment for many-electron systems[J].PhysRev, 1934, 46(7): 618-622.
[38] Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian 09[CP], Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
[39] Noyman M, Zilberg S, Haas Y. Stability of Polynitrogen Compounds: The importance of separating the σ and π electron systems[J].JPhysChemA, 2009, 113(26):7376-7382.
[40] Krevelen D W, Nijenhuis K. Properties of polymers [M].Beijing: Science Press, 2010.
[41] Cohen N, Benson S W. Estimation of heats of formation of organic compounds by additivity methods[J].ChemRev, 1993, 93: 2419-2438.
[42] Eaton P E, Zhang M X. Octanitrocubane: a new nitrocarbon[J].PropellantsExplosPyrotech, 2002, 27(1): 1-6.
[43] Agrawal J P. High energy materials, propellants, explosives and pyrotechnics [M]. Wiley-Vch Verlag GmbHCo. KGaA, 2010.
[44] Dobratz B M, Crawford P C. LLNL Explosives Handbook: Properties of Chemical Explosives and Explosive Simulants: LLNL [M]. 1985: 187-188 (UCRL-5299j-chg.2).
[45] Archibald T G. Synthesis and X-ray crystal structure of 1,3,3-trinitroazetridine[J].JOrgChem, 1990, 55(9): 2920-2924.
[46] Holland J H. Genetic algorithm[J].Science, 1992,11: 24-31.
[47] Holland J H. Adaption in natural and atificial systems [M]. The University of Michigan Press, 1sted, 2nded. Cambridge, MA: NIT Press, 1992: 102.
[48] 周荣敏, 雷延峰. 管网最优化理论与技术: 遗传算法与神经网络[M]. 郑州: 黄河水利出版社, 2002: 23.
ZHOU Rong-min, LEI Yan-feng. Theory and technology of the optimal tubes and nets: Genetic and algorithm and neural networks[M]. Zhengzhou: Huanghe Irrigation Press, 2002: 23.
[49] 卢小泉, 陈晶, 周喜斌. 化学计量学研究方法[M]. 北京: 科学出版社, 2013: 218.
LU Xiao-quan, CHEN Jing, ZHOU Xi-bin. Chemometrics Methods[M]. Beijing: Science Press, 2013: 218.
