高度线性增加的多米诺依次倾倒后能量的传递

白海峰，唐永成，黄志斌，李文波，林爽拿，钱 静，薛 迅

（华东师范大学物理系，上海200241）



高度线性增加的多米诺依次倾倒后能量的传递

白海峰，唐永成，黄志斌，李文波，林爽拿，钱 静，薛 迅

（华东师范大学物理系，上海200241）

摘 要：近似认为多米诺之间相互碰撞系统的角动量守恒，并且在各多米诺倒下的过程中，由于每块多米诺绕其支点转过的角度很小，因此而忽略在此过程中相互的作用力所做的功.由于能量传递与各多米诺的转动角速度相关，故可以推出高度线性增加的多米诺倾倒后能量的传递情况.多次实验角速度的实验值都大于理论值，但是实验值与理论值随多米诺的序数增加下降趋势与幅度大致相同.

关键词：多米诺；能量传递；倾倒；线性

本文所研究的问题由2011年国际青年物理学家锦标赛（International Young Physicists’Tournament，简称IYPT）的比赛题目给出：

8.Domino amplifier

A row of dominoes falling in sequence after the first is displaced is a well known phenomenon.If a row of“dominoes”gradually increases in height，investigate how the energy transfer takes place and determine any limitations to the size of the dominoes.

多米诺骨牌是一种风靡一时的游戏，受到国内外广大游戏爱好者的欢迎.它是一款集趣味性、智慧性、实践性于一体的游戏.在倾倒的多米诺相互联系的系统中，很小的初始能量就产生一连串的连锁反应，人们把这种效应称为多米诺骨牌效应或多米诺效应（Domino effect）.

我们注意到，国内外有关多米诺倾倒后能量传递问题的研究成果很多，但是有关高度逐渐增加的多米诺倾倒的研究成果较少.因此，我们认为这是一个很好的研究课题.

2011年国际青年物理学家锦标赛的这道题目中，“gradually increases in height”并未说明多米诺的高度是否随着多米诺的序数线性增加，另外也可能被理解成图1（a）和（b）的2种情形.

由于多米诺高度增加有多种情形，考虑到各种情形能量传递并不完全相同，在这里只讨论多米诺高度随序数线性增加的情况.

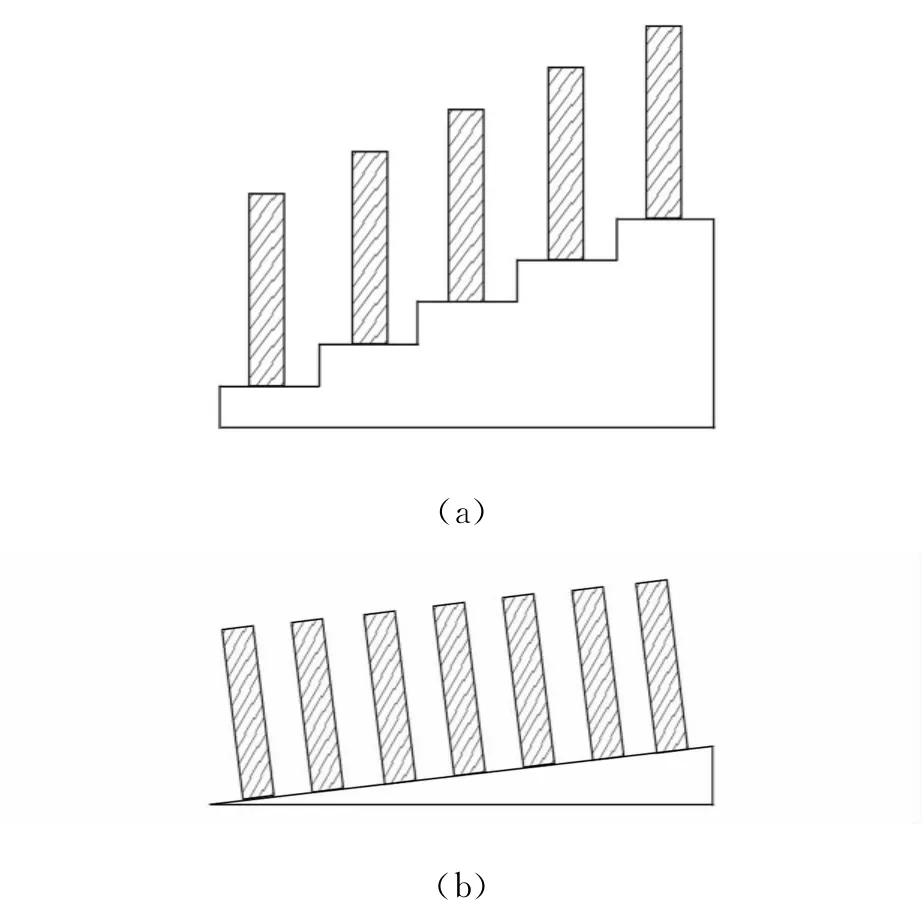
图1 多米诺的高度增加形式

第一块多米诺在受到微小的力的作用后，撞击下一块多米诺并使其倾倒，这样循环往复，对于等高的多米诺而言，其倾倒的速度会与其所用多米诺的几何尺寸、各多米诺之间的距离以及倾倒角度有关.在研究中建立了新的理论模型，并进行了大量实验对理论模型进行了验证，得出了较为满意的结果.

1 理论模型

为了使计算简单，考虑多米诺高度与其序数成正比的情形.设第1块多米诺的高度为h，质量为m，多米诺的序数为i（i＝1，2，3…），多米诺厚均为d，宽均为w，多米诺之间的距离均为s，则第i块多米诺的高度为

质量为

做出如下假设：

1）假设每块多米诺与地面间的摩擦力足够大，以至于它们和地面间都不会发生相对滑动.

2）忽略倾倒过程中多米诺相互间的摩擦.

3）近似认为整个多米诺系统在碰撞过程中角动量守恒.认为在多米诺相互碰撞的过程中相互间的作用力产生的力矩要远大于外力（比如重力）的力矩，因此忽略系统外力力矩.

对于已经相互接触的第N－1块与第N块多米诺之间，有几何关系（图2）如下：

对（3）式两边全微分有

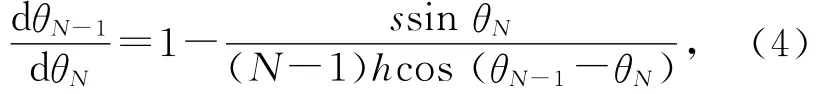
即

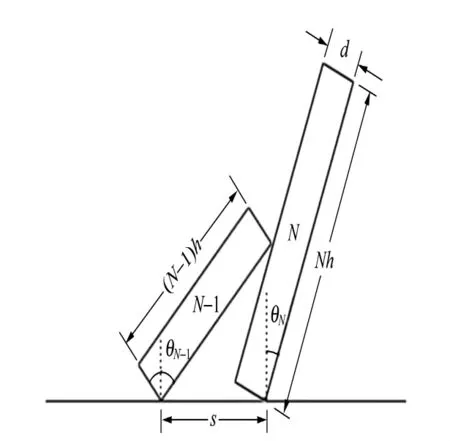
图2 第N－1与第N块多米诺间的几何关系

由（3）式和（5）式可得

令

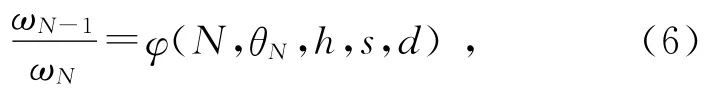
易知φ（N，0，h，s，d）＝1.则此时所有已经倒下的多米诺的动能总和为

对于第N－1块与第N块多米诺之间的碰撞过程，角动量守恒，则有

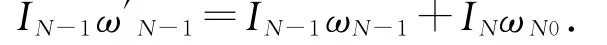
联立（5）式有

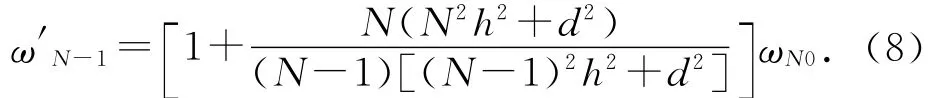
令

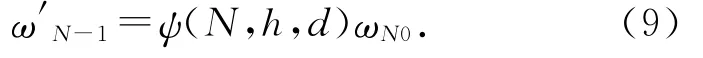
注意（9）式中ω′N－1为2块多米诺碰撞前瞬间第N－1块的角速度，前面所说的ωN－1为碰撞后的角速度.

由此，在这次碰撞中损失的能量为

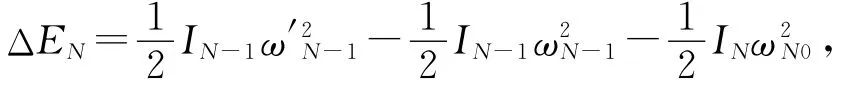
即

令

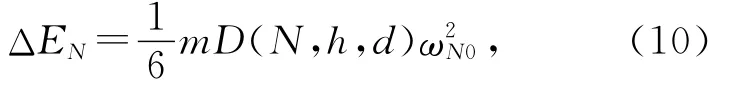
倾倒的全部N块多米诺由于碰撞损失的能量为

第N－1块多米诺倾倒过程中机械能守恒，则有

得

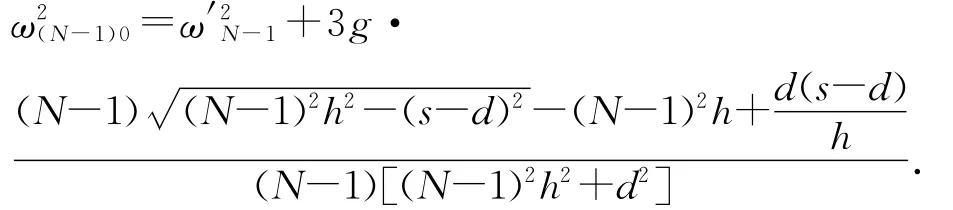
这就是倾倒初角速度的递推公式，其中有ω10＝0.

由此，各块多米诺倾倒的初角速度只与N，h，s，d有关，于是有

倾倒的全部N块多米诺由于碰撞损失的能量可以重新写成更为简洁的形式：

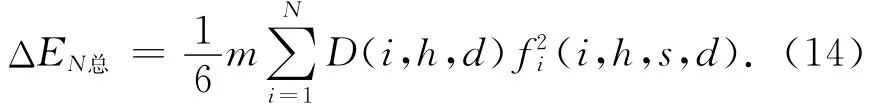
另外，从第N－1块多米诺碰撞第N块多米诺（称t1时刻），到第N块多米诺碰撞第N＋1块多米诺（称t2时刻）的过程中，θN－1从

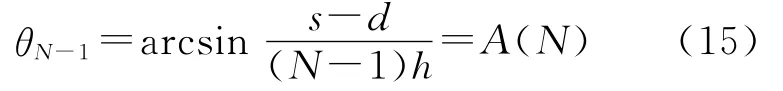
变化到

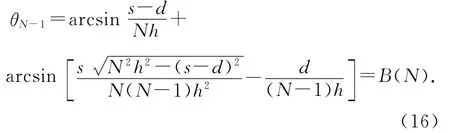
将后续实验中的参量代入绘出A（N）与B（N）的散点图，如图3所示，图中所用参量：h＝6cm，s＝4cm，d＝0.8cm.

图3 A（N）与B（N）的散点图

由图3可以看出，从t1时刻到t2时刻，在实验所给定的参量下θN－1的相对变化极小，因此认为在这个过程中，第N－1块多米诺对第N块多米诺所做的功可忽略不计.

由此还可以看出，在实验所给定参量的条件下，两者间的相对滑动所消耗的能量也很小，所以忽略摩擦力的影响.

再来看对多米诺大小的限制.容易得到：

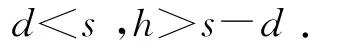
要使多米诺的连续碰撞不会中止，那么第N－1块多米诺对第N块多米诺的碰撞传递给第N块的能量，应至少能使第N块的重心到达和其支点的同一竖直平面内，情形如图4所示.则有

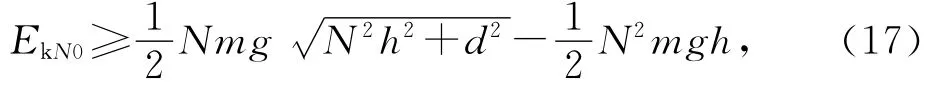
即

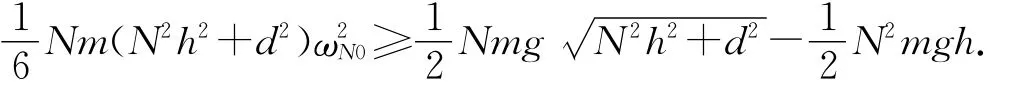
由（13）式则有

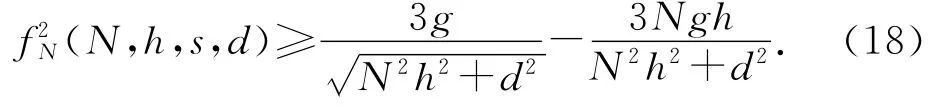
图4 多米诺的碰撞能量传递

2 实验验证

可以看出，（12）式的导出，既包括了第N－1块多米诺与第N块的碰撞过程，又包括了第N－1块多米诺的倾倒过程，并且ωN0在实验中较容易测量，所以可以利用实验来验证（12）式递推关系.

利用市售的玩具多米诺骨牌进行加工后，成为符合实验要求的多米诺.用不同规格的多米诺做了多次实验.

用Us－1011型DES光电门传感器测多米诺刚开始倒下时的挡光时间，进而计算出所求ωN0.表1为其中1次测量的实验数据和理论值的比较.第1块多米诺大小为：3.20cm×0.80cm× 6.00cm，多米诺之间的距离为4.00cm.

根据表1数据绘出的实验值和理论值的对比图如图5所示.

表1 实验值与理论值的对比

图5 实验值与理论值的对比图

多次实验的实验值都要比理论值要大，但是实验值与理论值随N下降趋势与幅度大致相同.我们认为造成该现象的原因可能是对于第N－1块向第N块所做的功估计不足，导致理论的初角速度小于实际的初角速度.另外，实验中用光电门传感器来测多米诺刚开始倒的挡光时间，进而估算其倒下的初角速度，该方法容易产生误差.综上所述，理论计算和实验方法都使实验值大于理论值.但是我们认为实验结果已经能够很好地验证了理论模型.

3 结 论

近似认为多米诺之间相互碰撞系统的角动量守恒，并且在各多米诺倒下的过程中，由于每个多米诺绕其支点转过的角度很小，因此忽略在此过程中相互的作用力所做的功.由于能量传递与各多米诺的转动角速度相关，故容易知道高度线性增加的多米诺倾倒后能量的传递情况.理论和实验符合得并不是非常好，我们认为造成这一现象的主要原因是对上述两点的近似处理.

参考文献：

［1］ van Leeuwen J M J.The Domino effect［J］.Am.J.Phys.，2010：78（7）：721－727.

［2］ Stronge W J.The domino effect：a wave of destabilizing collisions in a periodic array［J］.Proc.R.Soc.Lond.A，1987，409：199－208.

［3］ Stronge W J，Shu D.The domino effect：successive destabilisation by cooperative neighbours［J］.Proc.R.Soc.Lond.A，1988，418：155－163.

Energy transfer of toppling dominos whose heights increased linearly

BAI Hai－feng，TANG Yong－cheng，HUANG Zhi－bin，LI Wen－bo，LIN Shuang－na，QIAN Jing，XUE Xun
（Department of Physics，East China Normal University，Shanghai 200241，China）

Abstract：The angular momentum of domino collision system was conserved approximately.In the falling process of the dominoes，the turn angle of each domino around the pivot was small，the work of the interaction force could be ignored.The energy transfer among the dominoes whose height increased linearly could be obtained because the energy transfer could be associated with the rotation velocity of the dominos.Experimental results indicated that the angular velocity was greater than the theoretical value，but the trend and range were roughly the same.

Key words：domino；energy transfer；toppling；linearly

通讯作者：薛 迅（1963－），男，山东青岛人，华东师范大学物理系教授，博士，研究方向为粒子物理与场论.

作者简介：白海峰（1990－），男，山西忻州人，华东师范大学物理系2009级本科生.

收稿日期：2015－12－28

中图分类号：O313

文献标识码：A

文章编号：1005－4642（2016）03－0024－04

［责任编辑：任德香］