考虑动态损耗的超磁致伸缩换能器的多场耦合模型

黄文美　薛胤龙　王　莉　翁　玲　王博文

(电磁场与电器可靠性省部共建重点实验室(河北工业大学)　天津　300130)



考虑动态损耗的超磁致伸缩换能器的多场耦合模型

黄文美薛胤龙王莉翁玲王博文

(电磁场与电器可靠性省部共建重点实验室(河北工业大学)天津300130)

摘要在热力学理论、Jiles-Atherton模型、能量守恒定律和换能器结构动力学原理的基础上，考虑动态损耗带来的影响，建立了包含磁-机-热的耦合项的超磁致伸缩换能器的多场耦合模型。运用数值计算方法对所建立的模型进行了计算，计算结果与实验结果吻合较好，说明所建立的多场耦合动态模型能够描述驱动磁场和换能器的输出应变之间的关系，能很好地描述换能器的实际工作状态，为超磁致伸缩换能器设计研发提供理论指导。

关键词：超磁致伸缩换能器多场耦合模型动态损耗温度效应

0引言

超磁致伸缩材料(Giant Magnetostrictive Material，GMM)是一种新型智能材料，Terfenol-D作为其中的一种，具有磁致伸缩应变大、机电转换效率高和能量耦合系数大等性能。超磁致伸缩换能器是以此材料为核心元件构成的一种将电能转化成机械能的装置，结构紧凑，能量密度大，可广泛用于微位移控制、机械精密加工、金属探伤、水下物体探测等领域。

超磁致伸缩换能器在工作中表现出强非线性的磁-机-热多物理场耦合特性，多场耦合对换能器的作用异常复杂，这就使得考虑动态损耗的同时，建立能反映其换能器系统层次的多场耦合特性、频率相关的磁化过程以及动态磁滞非线性的模型更为复杂。为了能够有效模拟换能器的真实工作状态，为换能器的广泛应用提供理论基础，有必要建立换能器的非线性动态模型。文献[1，2]分别提出了基于能量的磁致伸缩材料的静态和动态磁滞模型，模型和实验结果吻合较好，但它们都只是磁致伸缩材料层次的模型，没有考虑换能器系统的整体层次。文献[3]基于热力学原理，建立了超磁致伸缩材料磁-机-热耦合本构模型，展现了强非线性特性，描述了温度对于磁致伸缩应变和磁化强度的影响，但没有考虑涡流及异常损耗，仅适用于低频阶段，且仍没有结合换能器层次进行考虑。文献[4，5]建立了超磁致伸缩换能器动态磁-机耦合模型，结合了换能器结构动力学原理，是建立在系统层次的模型，考虑了动态损耗的影响，然而这些模型忽略了温度效应的影响。文献[6]建立了考虑应力变化的换能器动态模型，并对温升对换能器的影响做了实验，表明温度是不可忽略的因素。文献[7]以磁致伸缩材料多场耦合为基础，建立了磁-机双向耦合的动态模型，但没有考虑负载引起的棒内应力和磁场变化，没有真正实现系统层次的耦合。文献中很少有模型从磁致伸缩换能器系统层次来描述其多场耦合特性。本课题组建立了超磁致伸缩材料的磁-弹-热多场耦合本构关系，建立了考虑动态损耗的磁-机-热多场耦合磁致伸缩换能器模型，并通过数值计算方法对其求解。

本文从弹性Gibbs自由能角度出发，在热力学关系、Jiles-Atherton模型、能量守恒定律、换能器结构动力学原理的基础上，考虑交流驱动时的动态损耗，建立了超磁致伸缩换能器的磁-弹-热多场耦合动态模型，利用此模型模拟换能器的输出应变在温度和动态损耗影响下的实际工作状态。

1超磁致伸缩换能器结构和工作原理

超磁致伸缩换能器的结构示意如图1所示。其工作原理为：在换能器的励磁线圈中通入交流电流，会有交变磁场产生，此时Terfenol-D棒在驱动磁场作用下发生沿棒方向的伸缩变化，从而完成将电磁能转换成机械能，以振动的形式来推动尾质量运动，实现位移和力的输出。图1中，配重的作用是确保Terfenol-D棒有单方向的位移输出；预紧螺栓和蝶簧的作用是向Terfenol-D棒提供适当大小的轴向预压应力，因为Terfenol-D棒在压应力的作用下会有更大的磁致伸缩应变；永久磁铁向Terfenol-D棒提供适当的偏置磁场，使Terfenol-D棒的机械频率等于驱动磁场的频率，从而避免“倍频”现象。

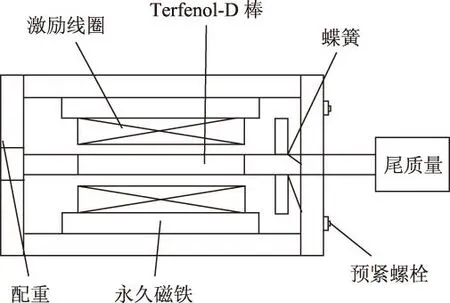
图1　超磁致伸缩换能器结构示意图Fig.1　Schematic diagram of magnetostrictive transducer

2考虑动态损耗的多场耦合模型

2.1磁致伸缩材料整体应变模型

Terfenol-D棒通常被等效为一个热力学系统来分析磁致伸缩材料复杂的磁-弹-热多场耦合关系，根据弹性Gibbs自由能以及对其物理意义和实验现象的分析，可以认为超磁致伸缩材料的应变可以写成三部分[8]，即

ε=εσ+εT+λ

(1)

式中，第一部分为仅由应力产生的应变，第二部分为仅由温度变化产生的热膨胀应变，第三部分是磁致伸缩应变，是超磁致伸缩换能器设计及模型研究的核心问题。D.C.Jiles[9]描述磁化强度与磁致伸缩之间的关系式为

(2)

式中，γi(σ)是和应力有关的参数，σ表示应力；M为磁化强度。式(2)体现了磁-机耦合的关系，但并未考虑温度的影响。基于式(2)，本文提出一个考虑温度效应的磁化强度与磁致伸缩之间关系的拓展模型，即

(3)

式中，ΔT为温度差值，ΔT=Ta-Tr，Ta为实际的环境温度，Tr为自旋再取向温度(对Terfenol-D来说，Tr=0 ℃)；γi(σ，ΔT)是与应力和温度有关的系数。为了方便实际应用，取i=2。其中常数项仅为应力温度系数，对多场耦合效应影响很小，从实用性角度出发，可以忽略，从而得到磁致伸缩表达式为

λ(M,σ,ΔT)=γ1(σ,ΔT)M2+γ2(σ,ΔT)M4

(4)

式中，γi(σ， ΔT)可用泰勒级数将其展开成关于应力温度的多项式，即

(5)

式中，γix是当ΔT=0时的关于应力的偏导数；γiy是当σ=0时的关于温度的偏导数，分别仅保留关于应力温度的线性部分，可得

γ1(σ,ΔT)=γ11+γ12σ+γ13ΔT

(6)

γ2(σ,ΔT)=γ21+γ22σ+γ23ΔT

(7)

式中，γ11、γ12、γ13、γ21、γ22及γ23为材料的磁致伸缩系数，结合实验曲线，在边界给定的情况下，可通过测量不同应力温度(如：σ=0 MPa；ΔT=20 ℃、40 ℃、60 ℃和ΔT=20 ℃；σ=5 MPa、10 MPa、15 MPa)下饱和磁化强度与饱和磁致伸缩获得一组齐次方程，求解结果见表1。

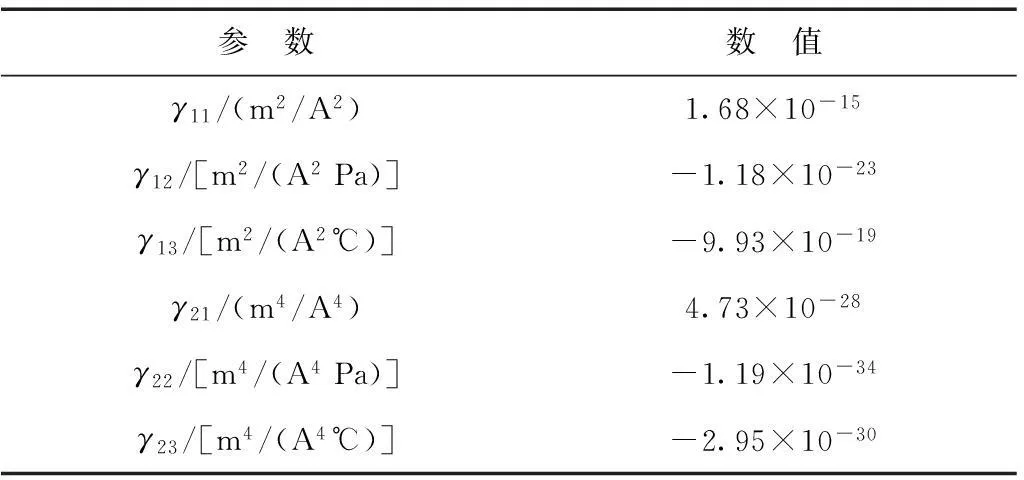
表1　磁致伸缩模型参数取值

因此，结合式(4)～式(7)，整理化简便可得磁致伸缩λ(M，σ，ΔT)的表达式为

λ(M,σ,ΔT)=γ11M2+γ21M4+σ(γ12M2+γ22M4)+

ΔT(γ13M2+γ23M4)

(8)

式中，前两项是仅与磁化强度有关的磁致伸缩，第三项是磁化强度和应力耦合引起的磁致伸缩，第四项是磁化强度和温度耦合引起的磁致伸缩。式(8)能清晰地体现换能器的多场耦合特性。从式(8)看出，式中的每一项都和磁化强度有关，由于磁致伸缩的六个系数确定，只要确定磁化强度，就能算出磁致伸缩应变的大小。

2.2磁化强度模型

有效磁场He将磁致伸缩模型和磁化强度耦合在一起来构成多场耦合的非线性模型。从自由能密度函数角度出发，可得到有效磁场标准形式为

(9)

式中，H为外加磁场强度；μ0为真空磁导率；α为畴壁相互作用系数。将式(8)代入到式(9)中得

σ(3γ12M+6γ22M3)+ΔT(3γ13M+6γ23M3)]

(10)

可将式(10)简写成

He=H+qM

(11)

这里

ΔT(3γ13+6γ23M2)]

(12)

为了使模型能够运用在动态加载的情况下，因此考虑了动态损耗对磁化过程的影响。根据微磁学理论，材料或多或少会存在缺陷，使得畴壁停在材料内不动，形成钉扎效应，无论静态还是动态，都会有钉扎损耗ΔLm，文献[10]给出了动态加载条件下铁磁材料中存在涡流损耗ΔLe和附加损耗ΔLa。

基于能量守恒关系，有

ΔWw=ΔWq+ΔLm+ΔLe+ΔLa

(13)式中，ΔWw为外加驱动磁场产生的能量；ΔWq为磁化过程中单位体积中的静磁能。分别代入各能量表达式有

-μ0∫MdHe=-μ0∫MandHe-μ0∫ξKB(1-cB)dMirr+

(14)

式中，Mirr为不可磁化强度；D为棒的直径；Sc为棒的横截面积；β为材料的几何因子，对于圆柱体，β=16；无量纲常数G0=0.135 6；H0是和材料畴壁相关的参数；ρ为材料的电阻率；ξ用来保证计算结果和其物理特性一致，在文献[11]中有注明；KB和cB分别为考虑温度T影响的钉扎系数和可逆因子，表达式分别为[12，13]

(15)

(16)

式中，K0为钉扎系数的初始值；c0为可逆系数的初始值。文献[3]中给出的可逆磁化强度Man表达式为

(17)

等式两边同除μ0以后再进行微分，则式(14)变为

(18)

基于Jiles和Atherton的假设[14]，有

(19)

这里，δ是用来保证理论计算和Terfenol-D物理特性一致的参数。

式(19)两边乘上dH/dt，可得

(20)

再结合复合函数求导法则，可得

(21)

将式(11)对t求导并代入式(21)，可得

(22)

结合式(18)～式(22)，整理可得磁化方程为

(23)

运用牛顿迭代法可求解磁化强度变化率dM/dt，从而能够计算出磁化强度，利用式(1)及式(8)求得Terfenol-D材料层次的应变，再结合下文的换能器的结构动力学原理来求解器件层次的换能器系统输出应变。

2.3换能器结构动力学模型

从换能器系统层次上看，换能器模型还必须考虑加负载的情况，同时要考虑动态应力σ对磁化过程及整体应变的影响，文献[15]简洁地给出了下一时刻动态应力的公式，即

(24)

式中，ΔL为磁致伸缩棒的长度变化量；KL为等效刚度矩阵，相比文献[16]中的动态应力复杂计算方法，其减少了计算时间，提高了效率，但未考虑棒本身阻尼的影响。基于结构动力学原理，文献[17]只是将磁致伸缩作为了换能器输出应变，给出了二阶暂态动力学模型，本部分基于这些已有模型对换能器系统的结构动力学模型进行了推导。

对式(4)Terfenol-D应变的简化表达为

(25)

式中

(26)

将文献[17]换能器的结构动力学模型中磁致伸缩λ(t)替换成ω(t)，得到改进的模型为

(27)

式中，u(t)为位移矢量；ML、CL分别为等效质量和负载等效阻尼系数矩阵；F[ω(t)]为激励矢量，各单元激励源表达式为

(28)

式中，φ′(x)为数值计算的过程量，在文献[17]中有说明。

通过对二阶暂态动力学方程(式(27))的求解，可以得到换能器末端t时刻的位移矢量u(t)，从而求得换能器的整体输出应变

(29)

式中，L为磁致伸缩棒的长度。

计算出t时刻的输出应变，完成对换能器输出的一次求解，再根据式(24)求解t+Δt时刻的动态应力，重新结合式(25)～式(29)，完成t+Δt时刻的计算，以此循环求解任意时刻的输出应变。

3计算结果与分析

利用本课题组的实验测试结果[8]及文献[16]中的部分数据，对所建立的磁致伸缩换能器系统的动态模型进行了数值计算。用Matlab编程，模型计算时间2 min左右。

图2为不同温度下的λ-M关系曲线。从图2可以看出，当环境温度一定时，随着磁化强度的增加，磁致伸缩增加。而当磁化强度为定值时，磁致伸缩随着温度的升高而减小。出现这种情况是因为温度升高，热扰动对磁畴内磁矩的有序排列增加，而磁化强度的增加不会削弱热扰动带来的影响。为了得到相同的磁致伸缩，100 ℃时需要的磁化强度要比0 ℃时大，因此磁致伸缩棒磁化过程中不能忽略温度带来的影响。

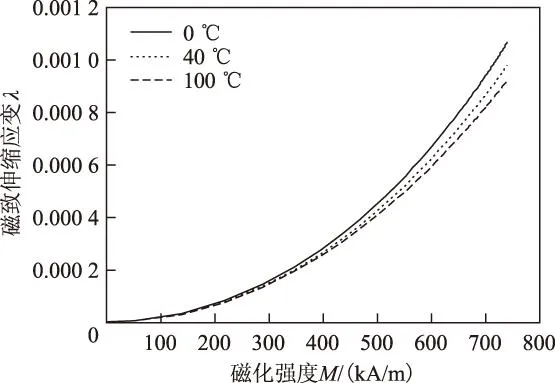
图2　不同温度下磁致伸缩-磁化强度关系Fig.2　Magnetostriction vs.magnetization at different temperatures

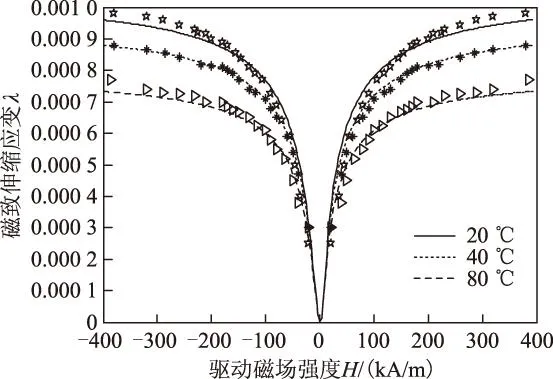
图3　不同温度的磁致伸缩-驱动磁场关系Fig.3　Magnetization vs.magnetic-field at different temperatures

图3是预应力为-10 MPa下、不同温度(20 ℃、40 ℃和80 ℃)的磁致伸缩曲线。图中符号为实验数据，连线为模型的计算结果。从曲线上可以看出，在中低磁场时，磁致伸缩随着驱动磁场增加得很快；当磁场增加到一定值时，大部分的磁畴已经转向了平行于驱动磁场的方向，磁致伸缩增加的幅度减弱，并逐渐趋向饱和。由于热扰动的存在，阻碍磁畴的旋转，使得温度高时，磁致伸缩值较低，温度对磁致伸缩饱和值的影响更为明显。所以，温度效应会影响磁致伸缩应变的大小，从而会影响换能器整体应变的输出。

利用所建立的模型，在驱动磁场为20 kA/m且没有偏置磁场、激励频率为1 kHz、环境温度20 ℃、预应力-10 MPa的情况下，对驱动磁场和磁化强度的关系进行了模拟。从图4可以看出，模型有效地描述了磁致伸缩棒的动态磁滞特性，理论计算结果和实验结果[8]吻合较好，偏差量不超过3.86%。由于动态能量损耗的影响使得产生的磁滞损耗相比于静态磁滞损耗要大得多。图5描述了换能器的整体应变和驱动磁场之间的关系[16]，可以看出，在动态加载的情形下，忽略动态损耗的理论预测结果明显高于换能器输出应变的实验值，同时磁滞回线的能量损耗也变小，而仿真和实验数据吻合较好，输出应变最大偏移量不超过4.21%，说明了所建立的考虑温度变化和动态损耗影响的模型能够准确描述超磁致伸缩换能器动态运行的特性，能够描述在加载情况下换能器的真实运行情况。

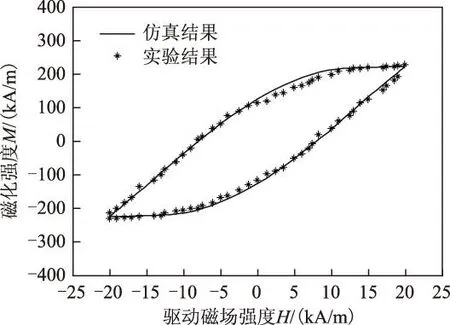
图4　频率为1 000 Hz的磁化强度-驱动磁场关系Fig.4　Magnetization vs.magnetic field at 1 000 Hz

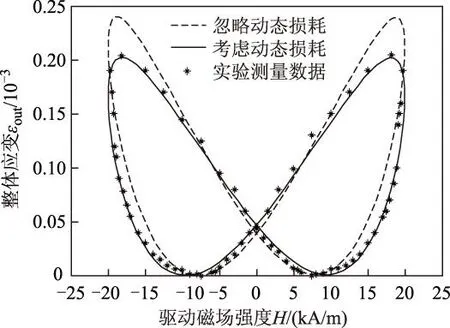
图5　换能器输出应变-驱动磁场的关系Fig.5　Output strain vs.magnetic field

4结论

为了反映超磁致伸缩换能器在实际动态加载下的工作情况，本文基于热力学理论、Jiles-Atherton模型、能量守恒定律、换能器结构动力学原理建立了考虑动态损耗的电磁-机械-热多场耦合模型，通过数值计算的方法模拟了换能器输出应变和驱动磁场的关系，模型数值计算结果和实验结果吻合较好，说明该模型能够准确反映换能器系统层次的多场耦合效应与频率相关的磁化过程和超磁致伸缩换能器的动态磁滞非线性特性。

参考文献

[1]Calkins F T，Smith R C，Flatau A B.Energy-based hysteresis model for magnetostrictive transducers[J].IEEE Transactions on Magnectics，2000，36(2)：429-439.

[2]Xu H，Pei Y，Fang D，et al.An energy-based dynamic loss hysteresis model for giant magnetostrictive materials[J].International Journal of Solids and Structures，2013，50(5)：672-679.

[3]Jin K，Kou Y，Zheng X J.A nonlinear magneto-thermo-elastic coupled hysteretic constitutive model for magnetostrictive alloys[J].Journal of Magnetism and Magnetic Materials，2012(324)：1954-1961.

[4]Huang W M，Wang B W，Cao S Y，et al.Dynamic strain model with eddy current effects for giant magnetostrictive transducer[J].IEEE Transactions on Magnectics，2007，43 (4)：1381-1384.

[5]翁玲，王博文，孙英，等.磁场和应力作用下的超磁致伸缩换能器的动态模型[J].电工技术学报，2008，23(12)：18-22.

Weng Ling，Wang Bowen，Sun Ying，et al.Dynamic model of giant magnetostrictive transducer under magnetic field and stress[J].Transactions of China Electrotechnical Society，2008，23(12)：18-22.

[6]曾建斌，白保东，曾庚鑫，等.考虑压力变化的超磁致伸缩超声换能器动态模型[J].电工技术学报，2012，27(10)：216-219.

Zeng Jianbin，Bai Baodong，Zeng Gengxin，et al.dynamic models of giant magnetostrictive ultrasonic transducer taking account into variable pressure[J].Transactions of China Electrotechnical Society，2012，27(10)：216-219.

[7]Jin K，Kou Y，Liang Y，et al.Effects of hysteresis losses on dynamic behavior of magnetostrictive actuators[J].Journal of Applied Physics，2011，110(9)：

093908(1-7).

[8]Wang Li，Wang Bowen，Wang Z H，et al.Magneto-thermo-mechanical characterization of giant magnetostrictive materials[J].Rare Metals，2013，32(5)：486- 489.

[9]Jiles D C.Theory of the magnetomechanical effect[J].Journal of Physics D：Applied Physics，1995，28(8)：1537-1546.

[10]Jiles D C.Modelling the effects of eddy current losses on frequency dependent hysteresis in electrically conducting media[J].IEEE Transactions on Magnetics，1994，30(6)：4326-4328.

[11]张纳，王博文，王莉，等.磁致伸缩、压电层状复合磁电传感器非线性动态有限元模型[J].电工技术学报，2012，27(7)：146-152.

Zhang Na，Wang Bowen，Wang Li，et al.Nonlinear dynamic finite element model for magnetostrictive/piezoelectric laminated composite magnetoelectric sensors[J].Transactions of China Electrotechnical Society，2012，27(7)：146-152.

[12]Wilson P R，Ross J N，Brown A D.Optimizing the jiles-atherton model of hysteresis by a genetic algorithm[J].IEEE Transactions on Magnetics，2001，37(2)：989-993.

[13]Raghunathan A，Melikhov Y A，Snyder J E，et al.Theoretieal model of temperature dependence of hysteresis based on mean field theory[J].IEEE Transactions on Magnetics，2010，46(6)：1507-1510.

[14]Iyer R V，Krishnaprasad P S.On a low-dimensional model for ferromagnetism[J].Nonlinear Analysis：Theory，Methods & Applications，2005，61(8)：1447-1482.

[15]Bottauscio O，Roccato P E，Zucca M.Modeling the dynamic behavior of magnetostrictive actuators[J].IEEE Transactions on Magnetics，2010，46(8)：3022-3028.

[16]Slaughter J C，Dapino M J，Smith R C，et al.Modeling of a Terfenol-D ultrasonic transducer[C]//SPIE’s 7th Annual International Symposium on Smart Structures and Materials，International Society for Optics and Photonics，2000，3985：366-377.

[17]Dapino M J，Smith R C，Flatau A B.Structural magnetic strain model for magnetostrictive transducers[J].IEEE Transactions on Magnetics，2000，36(3)：545-556.

黄文美女，1969年生，博士，教授，研究方向为磁性材料与器件、电机电器及其控制。

E-mail：huzwm@hebut.edu.cn(通信作者)

薛胤龙男，1989年生，硕士研究生，研究方向为磁性材料与器件、电机电器及其控制。

E-mail：984871361@qq.com

Multi-Field Coupling Model Considering Dynamic Losses for Giant Magnetostrictive Transducers

HuangWenmeiXueYinlongWangLiWengLingWangBowen

(Key Laboratory of Electro-Magnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of TechnologyTianjin300130China)

AbstractBased on the thermodynamic theory, the Jiles-Atherton model, the energy balance principle, and the structural dynamics principle of the transducer system, a multi-field coupling model of the giant magnetostrictive transducer is founded, which includes the magnetic-mechanical-thermal coupling terms and takes the dynamic losses into account. According to the proposed model, the relation between the magnet field and the output strain of the transducer is calculated using the numerical algorithm. Simulation results are in good agreement with the experimental ones, which indicates that the multi-fields coupling model considering the dynamic losses can well describe the actual working conditions of the transducer and provide theoretical guidance for design and development of the transducer in future.

Keywords：Giant magnetostrictive transducer, multi-field coupling model, dynamic losses, temperature effect

作者简介

中图分类号：TM153

收稿日期2014-06-19改稿日期2015-09-18

国家自然科学基金(51171057、51201055)，河北省自然科学基金(E2014202246)和河北省高等学校科学技术研究重点项目(ZD2015085)资助。