带变量核奇异积分算子与分数次微分算子在Morrey空间的加权有界性

薛 超（北京科技大学数理学院，北京 100086）



带变量核奇异积分算子与分数次微分算子在Morrey空间的加权有界性

薛 超
（北京科技大学数理学院，北京 100086）

摘要：研究了带变量核奇异积分算子T和分数次微分算子D(γ)在Morrey空间上的加权有界性．

关 键 词：加权的Morrey空间；带变量核奇异积分算子；分数次微分算子

1 主要结果

记Sn－1为瓗n（n≥2）上的单位球，dσ表示Sn－1上的Lebesgue测度，变量核奇异积分算子定义如下

其中，Ω（x，z）满足如下条件：

令m∈N，定义Hm为在Sn－1上的m阶球面调和函数空间，并记为Hm中的标准正交基，我们有

分别记T＊和T＃为T的伴随和T的拟伴值，我们定义为

再设T1T2为T1和T2的乘积，为T1和T2拟乘积［1］，其中

Iγ为γ阶Riesz位势算子空间Iγ（BMO）是空间在Iγ下的像，等价的说，一个局部可积函数b属于Iγ（BMO）当且仅当文献［3］证明了带变量核奇异积分算子与分数次微分算子Dγ在Lp（ω）的有界性．

对1＜p＜∞，称ω为Ap权（或者记为，如果有

其中，Q为边平行于坐标轴的方体．

经典的Morrey空间Lp，λ由Morrey于1938年提出［4］，Komori和Shirai［5］定义了加权Morrey空间Lp，κ（ω），并且研究了一些经典算子在其上的有界性问题．对于任意一个权函数ω，我们定义为Q的 Lebesgue测度，定义的权测度．

定义1［5］设1≤p＜∞，0＜κ＜1和ω为一个权函数，则加权Morrey空间定义为

则存在一个常数C＞0，使得

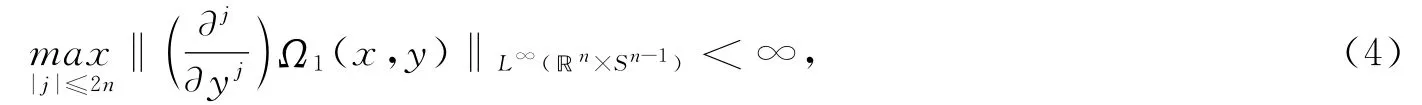
则存在一个常数C＞0，使得

2 一些引理

引理1［5］设1＜p＜∞，0＜κ＜1和ω∈Ap，如果T是一个Calderón－Zygmund奇异积分算子，则T在Lp，κ（ω）中有界．

给出一个权ω，对任意的方体Q，存在一个常数C，使得ω（2Q）≤Dω（Q），则ω满足倍增条件．当ω满足如上条件，我们定义ω∈Δ2．因此，当ω∈Ap，则有ω∈Δ2．由此引出引理2．

引理2［5］当ω∈Δ2，则存在一个常数D1＞1使得ω（2Q）≤D1ω（Q）．

引理4 设h（x）是－n－1阶齐次函数，且当｜x｜＞0时局部可积．当时有

设k（x，y）＝h（x－y）（b（x）－b（y）），根据文献［3］我们有

证明过程与文献［5］定理3．3与3．4证明类似．

应用引理4，证明过程与文献［3］类似．

引理6 令1＜p＜∞，0＜κ＜1和ω∈Ap．设Rk为Rizse变换，且

3 定理的证明

定理1的证明．

对于任意x，有

再根据式（3），对于k＝1，…，n，

再来看I2，根据引理5以及式（6），则

结合I1I2最终得到

根据引理5，式（6）和式（7），有

结合两式，则

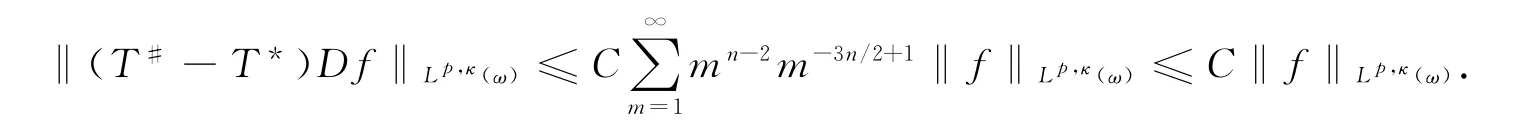
定理2的证明，记

如果Ω1（x，y）满足式（4）则，

如果Ω2（x，y′）满足式（3）则，

再根据引理5，则

则根据式（7）、式（8）及式（9）以及引理3，则

则

定理3的证明，不失一般性，只需证明（ⅱ）和（ⅲ）．由于Ω1（x，y）和Ω2（x，y′）满足式（4），可得

对于（ⅱ），如定理1的证明，可得

根据式（10），则

对于（ⅲ），记

参考文献：

［1］ A Calderón，A Zygmund．Singular integral operators and differential equations［J］．Amer．J．Math，1957（79）：901－921．

［2］ A Calderón，A Zygmund．On aproblem of Mihlin［J］．Trans．Amer．Math．Soc．，1995（78）：209－224．

［3］ Y Chen，K Zhu．Weighted norm inequality for the singular integral with variable kernel and fractional differentiation［J］．J．Math．Anal．Appl．，2015（423）：1 610－1 629．

［4］ C B Morrey．On the solution of quasi－linear elliptic partial differential equations［J］．Trans．Amer．Math．Soc．，1938（43）：126－166．

［5］ Y Komori，S Shirai．Weighted Morrey spaces and asingular integral operator［J］．Math．Nachr．，2009（282）：219－231．

［6］ G Di Fazio，M Ragusa．Interior estimates in Morrey spaces for strong solutions to nondivergence form equations with discontinuous coefficients［J］．J．Funct．Anal．，1993（112）：241－256．

Boundedness for the singular integral with variable kernel and fractional differentiation operator on weighted Morrey space

XUE Chao
（School of Mathematics and Physics，University of Science and Technology Beijing，Beijing 100086，China）

Abstract：This paper established the boundedness for the singular integral with variable kernel Tand the fractional differentiation operator D(γ)on the weighted Morrey space

Key words：weighted morrey spaces；singular integral operators；fractional differentiation operator

作者简介：薛 超（1991－），男，山西大同人，硕士研究生．

收稿日期：2015－08－10

文章编号：1672－2477（2016）01－0071－05

中图分类号：O174．2

文献标识码：A