小波分析在装裁机变速箱滚动轴承故障诊断中的应用探讨

谭世红

(贵州省遵义公路管理局，贵州 遵义 563000)

小波分析在装裁机变速箱滚动轴承故障诊断中的应用探讨

谭世红

(贵州省遵义公路管理局，贵州 遵义 563000)

主要讨论了小波分析在装裁机变速箱滚动轴承故障诊断中的应用，以求为未来装裁机变速箱滚动轴承故障诊断提供新的方法。

小波分析；装裁机变速箱滚动轴承；故障诊断

1 小波分析法基本理论

小波分析法属于一种有效的非平稳信号分析法，已经被广泛的应用在故障诊断中。其主要通过1组函数去表示逼近1个信号，而这组函数就被称为展缩小波函数系。在转换过程中，信号f(t)与展缩小波信号ψ(t)实现卷积分，并将特定的信号划分为多个用于表达不同频率带的数据。其基本计算公式为

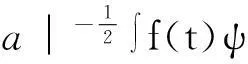
在上述公式中，ψ(t)代表震旦衰减且具有相应数值集的函数，称为基本小波函数，其中a是尺度函数，b是定位函数。

在计算函数f(t)时，可通过展开小波级数，并应用下列公式进行计算

在上述公式中，Cjk代表小波容许条件，属于一种有限的数值；ψjk通过小波函数平移、收缩而得到。

通常在小波分解中在，主要通过Mallat完成计算，这种计算方法可清晰表示不同计算条件下的小波分析问题，其主要表示方法为

在上述公式中，K代表特定的数值，包括1，2，3……N-1；fk代表信号采集过程中所形成的时域波形数据；N代表采样点数；j代表分解层数；h(n)、g(n)代表共轭镜像滤波器H点与G点的脉冲响应。

通过Mallat算法，将信号进行逐层分解，每层分解结果应该是上层分解所得到的低频信号分解成低频和高频2部分。每一次分解的数据量减半，因此分解后得到的低频成分和高频成分的时域分辨率比分解前信号降低一半。

在Mallat计算之后，信号可通过重构算法进行重构，其计算公式为

在上述公式中，K代表特定的数值，包括1，2，3……N-1。

重构算法的实质就是分解算法的逆过程，在每层重构之后，信号数量就会根据检测层数的增加而增加，因此，采用重构算法有利于进一步提高信号视频分辨效果。多数实践表明，小波分析的信号重构能力良好，基本上可以实现完全重构原有信号。

2 小波分析在装裁机变速箱滚动轴承故障诊断中的实例分析

2.1 诊断原理分析

在装裁机变速箱运转中，内部齿轮、滚动轴等均在工作，其所产生的振动信号会通过多种途径传递到箱体表面。此时，箱表面振动信号是所有信号叠加的效果。因此，需要从变速箱箱体表面测量变速箱的振动信号，在这个过程中，齿轮振动信号、轴不平衡信号等所产生误差均会等引起宽带随机响应都可以看作是平稳的随机过程，能量集中在低频区段，只有滚动轴承局部故障引起的高频瞬态响应是非平稳的，且能量集中在高频段。所以对滚动轴承故障信号分析来看，其他类型的振动信号均属于噪音。

2.2 数值计算

采用频谱分析法，诊断装裁机变速箱滚动轴承故障。在此之前，需要全方位了解滚动轴承的故障特征频率。就滚动轴承信号的实质而言，其频率分布较为广泛，当某一元件存在缺陷时，轴承在运行过程中出现不规律震荡。在分析该震荡的实际数据时刻按照下列公式进行计算

在上述公式中，fc代表外圈故障特征频率；D代表轴承节径；d代表滚动体直接；α接触角。

根据子算得出，信号采集频率为8 000 Hz。

通过对不同阶段的小波分解结果进行分析，建立各层细节重构图；再对不同层的细节进行FFT转化，得到不同层频谱的细节数据，并从各层细节频谱中我们发现装载机变速箱滚动轴承的外圈故障频率包含在小波第7层分解的细节中。最后统计计算结果，发现第7层的最大振幅频率为62.5 Hz，与上述公式中60.50 Hz的结果相似，说明其诊断效果具有科学性。

2.3 基于第二代小波方法的理论分析

(1)基本理论

在当前小波分析技术中，第二代小波方法的应用范围正在逐步扩大。在实际故障测量中，被分析的信号具有局部相关特点，在相邻样本相关性处理中，相关样本之间具备良好的相关性。因此在应用过程中，可以将所测的信号划分为奇数、偶数两个序列，并保证两个序列之间具备较高的关联程度(在特定的精度下，可以通过任意一组序列来计算另一个序列的全部数值)。例如，可以通过偶数样本序列的若干个样本，预测奇数序列中相同位置的数据，再统计数据间的细节系数。若奇数样本中的数据与实测值一致，且两者之间的值差是理想的，就可以判定细节系数取零。

在第二代小波方法处理中，会发现部分预测结果的差与预测流程，不能保留奇数序列与偶数序列之间的性质。此时可发现，第二代小波变换与经典小波分析具有一致性，都是要将传统的序列转化为更加精炼的表述方式。

(2)第二代小波的轴承故障定量识别

若轴承的某一部位出现损伤，那么轴承在运转过程中，可能会多次的向损伤位置施加力，这种施加行为所持续的时间虽然短暂，但依然能够出现构件变形现象，并且出现自由衰减振动。随着轴承运转的不断深入，这种振动会重复出现，最终出现振动信号幅值调制的现象。Hilbert变换包能快速的提取轴承损伤过程中所产生的特征频率信息。

Hilbert变换包的基本工作原理为：(1)能计算信号的Hilbert变换；(2)以信号为实部，Hilbert变换对为虚部，分析信号构成；(3)通过分析信号模，获取采样信号包络。

3 结 论

(1)装裁机变速箱滚动轴承出现故障时，振动信号不平稳，此时如果采取传统的傅里叶法，难以获得良好效果。此时，需要采取小波分析法，全方位分析变速箱轴承振动的信号与频域。(2)装裁机变速箱滚动轴承中的滚动表面出现疲劳剥落磨损的现象时，所产生的振动信号会包含上述现象。因此，需要正确认识到不同冲击成分对变速箱滚动轴的影响，并正确认识到其他冲击所产生的振动现象。(3)采用Matlab的小波分析工具与信号处理工具箱，能正确认识到装裁机变速箱滚动轴承的故障，并通过频谱分析及时解决这一故障。(4)采用小波分析法在装裁机变速箱滚动轴承故障诊断中的作用明显，在故障信号未经过任何处理的情况下，能有效解决故障诊断问题，值得在生产实践中做进一步推广。

[1] 卜伶俐，郭建英，蒋凤林.小波分析与Hilbert分析在滚动轴承故障诊断中的应用[J].哈尔滨理工大学学报，2008，13(2)：82-86.

[2] 杨柳松.基于小波分析与神经网络滚动轴承故障诊断方法的研究[D].东北林业大学博士学位论文，2013.

[3] 朱益军，李晓东，李臻.小波分析在煤矿胶带机滚动轴承故障诊断中的应用[J].电子世界，2014，(12)：47-49.

Discussion on the application of wavelet analysis in the fault diagnosis of loader gearbox rolling bearing

TAN Shi-hong

(Zunyi Highway Administration Bureau of Guizhou Province, Zunyi，Guizhou 563000,China)

Mainly discuss the application of wavelet analysis in the fault diagnosis of loader gearbox rolling bearing, aiming to provide a new way to solve this problem. This paper introduces the way of wavelet analysis at first, and analyzes its foundation by using the basic principle and computing method. Combined with example, discuss if it can be used in loader gearbox rolling bearing.

wavelet analysis; loader gearbox rolling bearing; fault diagnosis

2015-10-12

谭世红(1964-)，男，贵州湄潭人，中级，主要从事公路管理方面研究。

U472.6

C

1008-3383(2016)02-0122-02