机非混行条件下路内停车带设置规模研究

刘 聪，牟振华

(北京工业大学交通工程北京市重点实验室，北京 100124)

机非混行条件下路内停车带设置规模研究

刘 聪，牟振华

(北京工业大学交通工程北京市重点实验室，北京 100124)

根据机动车流量及非机动车流量只提出了Ⅲ级次干路在机非混行条件下路内停车二要素的推荐值，未来需对其他类型道路机非混行条件下路内停车二要素作进一步的分析研究。

路内停车；机非混行；停车带长度；避让带长度；仿真评价

1 机非混行条件下路内停车带设置规模模型

1.1 研究情况及假设

由于机非混行条件下的路内停车只发生在不设机非分隔带的道路上，所以根据表1可知，不设分隔带的城市道路有次干路和支路，这里我们只研究设2条双向机动车道的次干路，即本文研究Ⅲ级次干路在机非混行条件下设置间隔排列式停车带的情况。

本文所要建立的机非混行条件下路内停车模型受很多因素的干扰，譬如车辆的类型及停车带内车辆的驶入/驶离等都会对道路的实际通行能力产生影响。下面为了简化分析，对路内停车提出以下假设。

(1)停放车辆均为小型车，并以平行式停放。

(2)停放车辆只能占用最靠近路缘石的一条车道。

(3)模型中，始终把路内停车看成静态地停在路段上，不考虑停放车辆的到达驶离对动态交通的影响。

1.2 机非混行条件下路内停车二要素推荐值的确定

相同道路条件下，道路的实际流量对停车带长度及避让带长度的确定影响最大，所以我们根据V/C值(如表1所示)，针对Ⅲ级次干路确定设置间隔排列式路内停车的停车带长度及避让带长度，提出一个推荐值。其中V/C是实际交通量与通行能力之比，III级次干路通行能力为1 600 pcu/h。

表1 占用非机动车道设置停车泊位的V/C比值要求

非机动车单侧道路高峰小时V/C泊位设置0≤V/C<0.7可设置0.7≤V/C<0.9有条件的可设置V/C≥0.9不可设置

表2 城市道路路段一条车道的通行能力

杨晓光等人提出一个计算公式

d=D-L1-L2

式中：D为两交叉口间距离；L1为前方交叉口进口道最大排队长度加15～20 m；L2为上游交叉口对向进口道最大排队长度加15～20 m；d为允许设置路边停车区段长度。

一般，如果d<20 m，则不宜设置路边停车车位。

次干路交叉口间距一般为350～500 m，计算时取最大值500 m。由于设置城市路内停车泊位不可避免要影响道路的通行能力，因此设置时应考虑规模效应的要求。一般一组停车泊位长度不宜低于20 m，即当需要设置的停车泊位在 3个以上时才考虑设置。但连续设置的路内停车泊位长度过长，将对出入周边建筑造成不便，并且有可能影响到邻近交叉口的交通秩序。因此，在标准中应规定单组路内停车泊位长度不应超过80 m，最小不宜低于20 m。

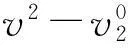
考虑到非机动车要减速进入避让带及机动车与非机动车之间的摩擦干扰等其他因素会使机动车并不能按期望加速度加速，这里L取30 m。确定避让带长度后，再根据非机动车流量的大小确定每100 m中避让带出现的个数。最后根据V/C值提出机非混行条件下路内停车二要素推荐值，其中机动车道一条车道设计通行能力为1 600 pcu/h。根据道路通行能力理论,非机动车道设计通行能力为900 veh/h。推荐值见表3。

表3 机非混行条件下III级次干路路内停车二要素推荐值

机动车V/C机动车V/(pcu/h)非机动车V/C非机动车V/(veh/h)停车泊位数n1/个停车带长度l1/m每一百米避让带个数n2/个0.22200127210.152000.44400106010.6660084820.22200116610.34000.4440095420.6660074220.22200106010.456000.4440084820.6660063620.2220095420.68000.4440074220.6660053020.2220084820.7510000.4440063620.666004243

2 基于VISSIM的路内停车仿真评价

用VISSIM软件对Ⅲ级次干路机非混行条件下路内停车模型进行仿真，分别得到小汽车、公交车和非机动车在相应机动车流量及非机动车流量下的500 m路段上的延误，其中不同流量对应着不同的设置情况，具体如模型中提出的推荐值所示。其延误值如表4、表5、表6所示。VISSIM3.7中流量单位均为veh/h。

由于仿真时测延误所选取路段长度存在一定的误差，所以得到的数据难免会有一些微小的波动，我们只按总体方向来分析。

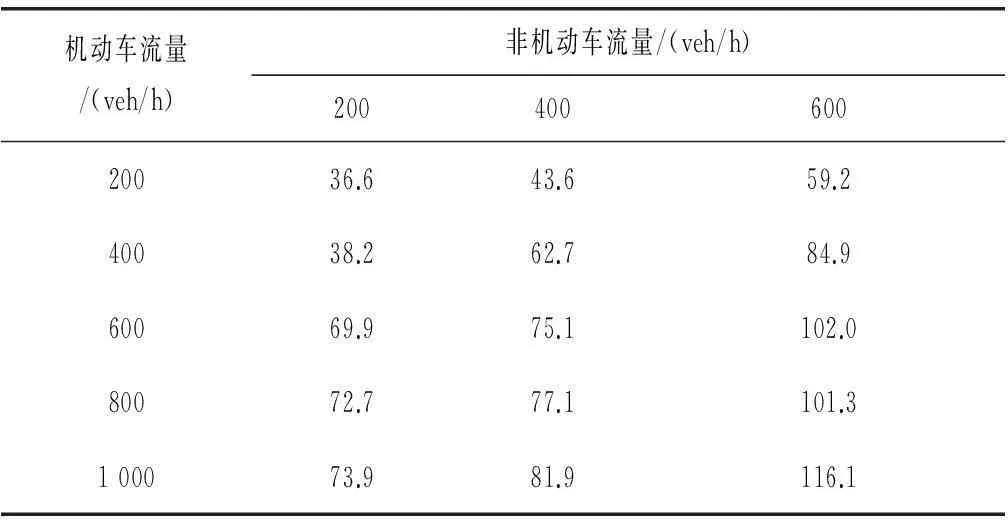
表4 小汽车延误 /s

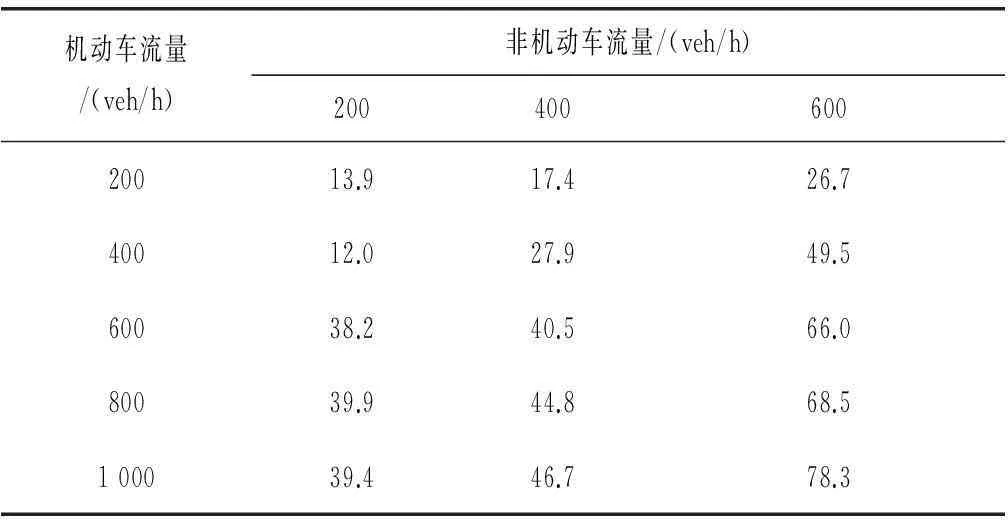
表5 公交车延误 /s

表6 非机动车延误 /s

由仿真后得到的延误可知：小汽车延误、公交车延误及非机动车延误随机动车流量和非机动车流量的增加而增加，当非机动车流量为200 veh/h，机动车流量为200 veh/h时，小汽车延误、公交车延误及非机动车延误分别为36.6 s、13.9 s、0.9 s，对于Ⅲ级次干路来说均较小。但当非机动车流量为600 veh/h，机动车流量为1 000 veh/h时，小汽车延

误、公交车延误及非机动车延误分别激增为116.1 s、78.3 s、17.3 s。

(1)当机动车流量小于600 veh/h且非机动车流量小于400 veh/h时，路边停车对机非混行系统影响不大，机非干扰程度属轻度。

(2)当机动车流量大于800 veh/h且非机动车流量大于600 veh/h时，路边停车对机非混行系统影响很大，机非干扰程度属重度。

(3)其他组合场景下，机非混行系统受路边停车影响变化平缓，机非干扰程度属中度。

(4)由表4、5、6可知，机动车比非机动车更易受到机非干扰冲突的影响，路边停车导致的机非冲突对机动车运行的影响最大。

当机动车流量为1 000 veh/h且非机动车流量为600 veh/h时，小汽车延误、公交车延误及非机动车延误均达到最大，其中小汽车延误为116.1 s，不到120 s，在可接受的范围内。由于Ⅲ级次干路条件有限，所以当机动车流量大于1 000 veh/h接近设计通行能力时就不宜设置路内停车了。因此机非混行条件下路内停车二要素推荐值是合理的。

3 结 语

本文建立了机非混行条件下路内停车模型，根据机动车及非机动车流量提出了适合我国的Ⅲ级次干路在机非混行条件下路内停车二要素的推荐值。基于VISSIM对机非混行条件下路内停车模型进行仿真，得出机动车及非机动车延误，发现机动车、非机动车和机非混行系统的平均延误随着机动车和非机动车流量增加而增加。当机动车流量为1 000 veh/h且非机动车流量为600 veh/h时小汽车延误最大，基本上接近可接受延误的上限。

[1] 魏岗. 路内停车泊位设置规模研究[J]. 西安: 长安大学, 2009.

[2] 陈竣，梅振宇，王炜.混合交通流条件下基于路内停车设置的路段车速阻滞模型[J].土木工程学报, 2007.

[3] 陈竣，王炜，梅振宇.路边停车带设置对混合车流速度影响分析[J].交通运输系统工程与信息,2005.

Scale study of curb parking in mixed condition

LIU Cong, MOU Zhen-hua

(Beijing Transportation Engineering Key Laboratory, Beijing University of Technology，Beijing 100124,China)

Flow according to the motor vehicle and non-motor vehicle traffic Ⅲ grades distributor roads are brought forward in the machine not only human conditions inside road parking motorised recommended value of two elements, the future need to other types of road machine of human under the condition of motorised parking within two elements for further analysis and research.

curb parking; mixed condition;parking-strip length;avoiding-belt length;simulation evaluation

2015-11-22

刘聪(1989-)，女，山东人，硕士研究生，研究方向：交通运输规划与管理。

U491 文献标识码：C 文章编号：1008-3383(2016)02-0141-02