考虑可交易路票策略的随机用户均衡模型及算法
2016-05-09韩飞程琳
韩 飞 程 琳
(东南大学交通学院,南京 210096)
考虑可交易路票策略的随机用户均衡模型及算法
韩飞程琳
(东南大学交通学院,南京210096)
摘要:为了弥补以往路票均衡模型中假设出行者知道准确路径费用的不足,对可交易路票策略下的随机用户均衡(SUE)分配问题进行了研究.首先,明确了在给定路票策略下交通网络达到均衡状态时的网络流量均衡和路票市场均衡条件;然后利用2个构造函数的相关数学性质建立了等价的通用型路票SUE模型,在出行者感知误差服从Gumbel分布假设下,将该模型化简为Logit型路票SUE模型,并给出了路票均衡价格唯一性的充分条件.由于传统MSA算法无法求解路票SUE模型,因此提出一种高效收敛的拉格朗日对偶算法.算例结果表明,该算法在不同步长序列和离散参数水平下均具有较好的收敛性,而且步长序列对算法收敛速度的影响比离散参数的影响更加显著.
关键词:可交易路票策略;随机用户均衡;路票价格;拉格朗日对偶算法
引用本文:韩飞,程琳.考虑可交易路票策略的随机用户均衡模型及算法[J].东南大学学报(自然科学版),2016,46(1) : 215-220.DOI: 10.3969/j.issn.1001-0505.2016.01.035.
拥挤收费在理论上被多次证明可以有效缓解城市交通拥堵,但在实际应用中却由于社会公平性、税收中性等问题而难以得到广泛应用.为了设计出既能有效治堵又能被公众接受的治堵策略,许多学者开始研究一种新颖的交通需求管理手段——可交易路票策略,或可交易行驶权证策略(tradable credit scheme).由于该行驶权证的调控作用类似于我国计划经济时期中的粮票,因此本文称为路票.该策略的主要思想是:首先交通部门在特定时间段(如每季度)初始时向所有具备资格的出行者免费发放相同数量的路票,然后出行者使用各路段时交纳相应数量的路票,路票可以在市场中自由交易,路票价格完全由市场供求关系决定,路票到期后自动失效以避免路票囤积.交通部门只作为监管部门,通过调控路票初始发放量和每个路段的路票收取量,从而实现交通系统的最优化目标.为了定量描述可交易路票策略对交通网络中出行需求的调控作用,Yang等[1]建立了基于可交易路票策略的用户均衡(user equilibrium,UE)模型(简称路票UE模型),并讨论了实现系统最优(system optimal,SO)的路票策略以及pareto-improving SO路票策略,并拓展到弹性需求情形,由此验证了该策略解决交通拥堵问题的有效性和可行性.Wang等[2]、Zhu等[3]在该研究基础上进一步考虑了不同出行者的时间价值异质性,并利用变分不等式建立了多用户类的路票UE模型.Nie[4]研究了在两类路票市场中交易成本对于SO路票策略调控能力的影响,发现在拍卖市场中该策略可以实现路网系统最优,而在议价市场中不可能实现路网系统最优.另外,其他关于可交易路票策略下的网络均衡模型有混合出行行为下的路票均衡模型[5]、考虑出行者损失厌恶行为下的路票均衡模型[6]等.
尽管上述文献从不同角度对可交易路票策略治理交通拥堵的有效性展开了研究,但其理论建模基础都是UE模型.UE模型假设出行者对于出行费用具有准确的认知,显然这与实际情况并不相符,受现实中出行者认知能力局限性和出行时间不确定性等因素影响,出行者不可能准确知道各条路径的出行费用,因而只能根据其感知的路径费用来选择路径.另一方面,SUE模型可以明确考虑出行者对于出行费用的感知误差及其所服从的概率分布,如Gumbel分布、正态分布等,相比UE模型来说,采用SUE模型来研究可交易路票策略显然更加合理,也更加符合实际.由于考虑可交易路票策略的SUE模型(简称路票SUE模型)无法像路票UE模型那样,通过简单地添加一个线性路票约束条件来建立,因此,本文首先建立了2个新的构造函数,通过运用这2个构造函数与原始对应函数之间的数学转换关系建立了一个极小值模型,并证明了该模型即为等价的路票SUE模型;其次,由于传统的MSA(method of successive averaging)算法无法求解路票SUE模型,本文进一步设计了高效且收敛的拉格朗日对偶算法,并利用算例验证了该算法的有效性.
1 模型
1. 1网络均衡条件
假设有向图G = (N,A)表示一个强连通交通网络,其中,N为节点集合,A为路段集合.W为所有OD对集合,qw表示OD对w∈W之间的出行需求.R = (Rw,w∈W)为所有工作路径集合,其中Rw表示OD对w∈W之间所有工作路径集合.(K,ka)表示一个给定的路票策略,K表示交通部门向出行者发放的总路票数量,即,其中表示每个出行者所获得的初始路票数量,ka表示路段a∈A上的路票收取数量.此外,分别表示路径r∈Rw上的流量和总广义费用,va和ta分别表示路段a∈A上的流量和旅行时间.由此,可以得到给定路票策略(K,ka)下的可行的网络流形态集合Φ(假设非空),其表达式为

由于现实生活中出行者对于实际出行费用会存在感知误差,因此假设在给定路票策略为(K, ka),则出行者感知的路径广义费用等于真实的路径广义费用加上感知误差,即


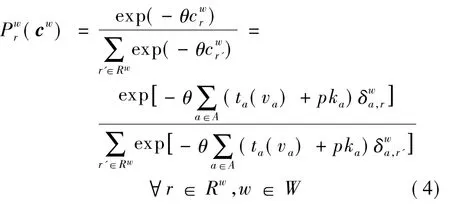
式中,θ>0为描述出行者对路网熟悉程度的离散参数.至此,可以知道在路票策略(K,ka)下交通网络达到均衡状态时,网络流量(frw,va)∈Φ和路票价格p必然满足如下网络均衡条件:

网络均衡条件式(5a)表示当交通网络达到均衡状态时,网络流量满足SUE配流原则;式(5b)表示路票市场均衡条件,即只有当所有发放的路票都被完全使用时,路票均衡价格才为正数,此时路票策略可以有效调控出行需求.
1. 2等价的路票SUE模型
传统无约束SUE模型的特殊性使得相应的路票SUE模型的建立无法采用路票UE模型的建立方法,即在传统SUE模型中添加一个线性路票约束所得到的最小化模型,其Kuhn-Tucker一阶最优性条件(KKT条件)不等价于网络均衡条件(5).为了建立相应的等价最小化问题,本文针对路段旅行时间函数ta(x),a∈A定义如下构造函数[7]:∈Φ,均存在连续可微的向量函数
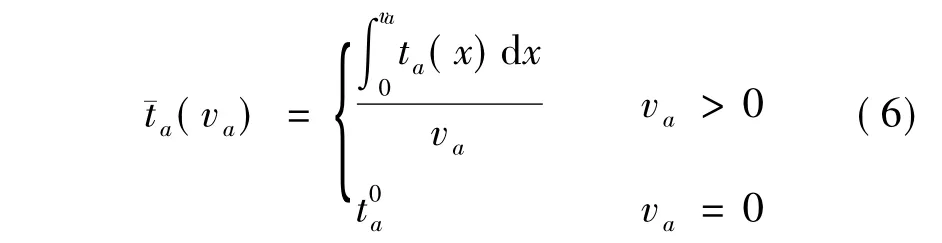
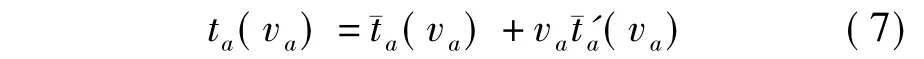
同时,根据文献[8]可知,对于任意正的可行路径流量形态(,满足如下条件:
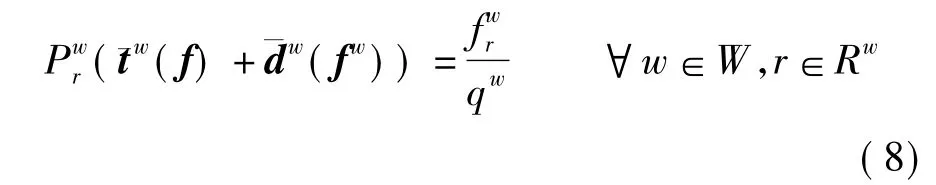
通过分析以上相关数学式的数学特性,可以为网络均衡条件式(5)建立如下等价的最小化数学模型(即路票SUE模型P1) :

定理1模型P1与路票策略(K,ka)下的SUE分配问题等价.
证明模型P1的拉格朗日函数为

式中,μw,ρ为相应约束条件的对偶变量.由KKT条件有
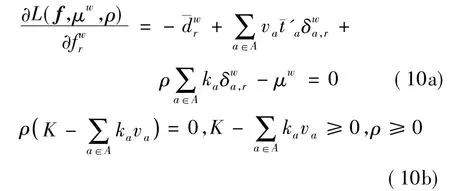
将式(10a)、(7)代入式(8),可以得到
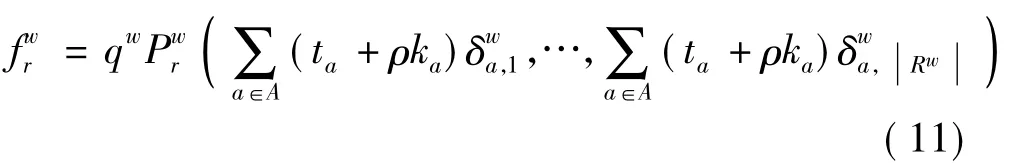
显然,由式(10b)、(11)可知,上述所建立模型P1的KKT条件正好是路票策略(K,ka)下的网络均衡条件,且对偶变量ρ即为路票均衡价格,故定理1得证.
模型P1是一个通用的路票SUE模型,当假设出行者感知误差服从正态分布时,可以得到Probit型的路票SUE模型;而假设感知误差服从Gumbel分布时,可以得到Logit型的路票SUE模型,此时由文献[8]可知

将式(12)、(13)代入模型P1,经过简单推导可以得到如下Logit型路票SUE模型(模型P2)的解析表达式:
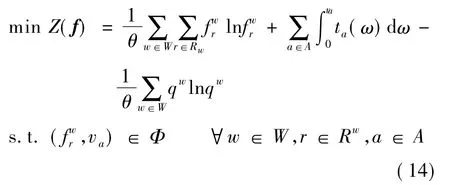
可以看出,模型P2和传统Logit型SUE模型[9]非常类似,除了目标函数中多了一个常数项外,唯一的区别就在于模型P2多了一个线性的路票约束条件.由于传统的Logit型SUE模型是一个凸规划问题,具有唯一最优解,因此,模型P2显然也是凸规划问题[9],同样也具有唯一最优解.
相对于模型P1来说,模型P2具有明确的解析表达式,同时大幅减少了计算量.因此,下面本文在模型P2的基础上进一步展开研究.
尽管在网络均衡状态时SUE网络流量解唯一,但是路票价格并不一定唯一,下面给出路票价格p唯一性的充分条件.
定理2当交通网络在路票策略(K,ka)下达到网络均衡状态时,如果至少存在一个OD对有2条路径上的路票收取总量不同,那么均衡路票价格p必定唯一.
证明当路票总量发放过多时,路票会有剩余,即路票总量约束为非活性约束,此时路票价格唯一,且p = 0.当所有路票被完全使用时,路票总量约束为活性约束,此时p>0.不失一般性,假设OD对w之间存在2条路票收取量不同的路径r1,r2∈Rw,根据Logit型SUE配流原则,可以得到

从而可以进一步得到均衡路票价格p的表达式:

显然,此时路票均衡价格p由式(16)唯一确定.故定理2得证.
在实际交通网络中,由于备选路径的多样性,定理2通常都是成立的.另外,路票价格p =0意味着对应的路票策略没有起到调控交通需求的作用,即是一个无效的路票策略,因此需要尽量避免.本文假设所给定的路票策略均有效,即可用如下有效路票策略集合Ψ来界定:

确认发生鸡痘的情况下,首先要对鸡痘的类型进行辨别。如果发生的是皮肤型鸡痘,在病情不严重的情况下可以不予管理,病情较重的可以通过对痘痂进行消毒和剥离,并涂抹紫药水的方式进行治疗。
2 算法
由于路票SUE模型P1和P2都带有额外的线性约束,因此求解传统SUE模型的MSA算法无法适用,为了设计一种通用的高效收敛的求解算法,本文提出如下拉格朗日对偶算法.
①初始化.令初始路票价格p0>0,令迭代次数n =1,容忍误差ε=10-4.
②计算路段旅行时间修正后的SUE解.将原始路段旅行时间函数{ ta(va),a∈A}修正为{ ta(va) +kap(n),a∈A},然后调用一次MSA算法,得到相应的SUE路段流量解{ va(p(n)),a∈A}.
④更新当前路票价格p(n).按照下式更新当前路票价格p(n):
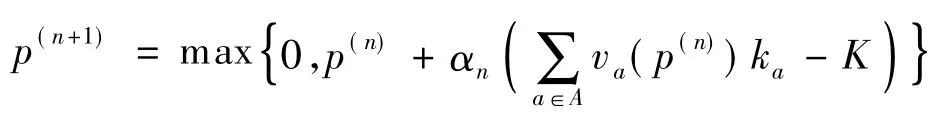
式中,{αn,n = 1,2,…}为预设的步长序列,且满足条件0<αn<1,<∞,本文取αn= 1/n.
⑤进行下一次迭代.令n = n +1,然后返回步骤②.
上述算法中,P+[p(n)+αnL'(p)]为非负投影,L(p)为模型P1的拉格朗日对偶函数,即L(p),其对p求导可得,因此将其代入后可得到非负投影表达式.由文献[10]中定理
2. 7关于次梯度投影法的收敛性可知,上述拉格朗日对偶算法必然会收敛到最优解.
3 算例
本文选择经典的Nguyen-Dupuis网络[11]作为算例,该网络有13个节点、19条边和4个OD对,如图1所示.路段阻抗函数为标准的BPR函数,即
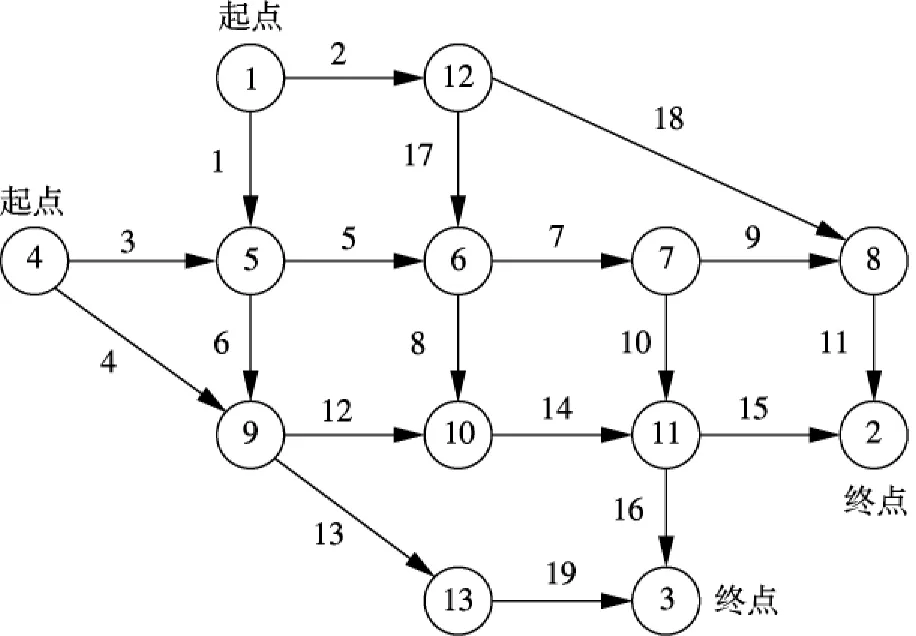
图1 Nguyen-Dupuis网络及路段属性参数

表1 Nguyen-Dupuis网络各路段自由旅行时间及容量
为了说明可交易路票策略对交通网络拥挤状况的改善作用,本文将路票策略实施前后的SUE路段流量进行对比,结果见表2.从表中可以看出,给定的路票策略可以有效缓解网络中部分路段的拥堵状况,如路段9,10的交通饱和度分别由1. 31,1. 20降为1. 17,1. 09.同时,路网总出行时间由77 227. 66减少为76 145. 72,由此可以说明设计合理的可交易路票策略不仅能够改善路网中部分瓶颈路段的拥堵状况,还能提高整个交通系统的出行效率.
为了说明拉格朗日对偶算法的收敛特性,本文分别对不同步长序列和不同离散参数水平下的算法收敛趋势进行对比(见图2和图3).由图2可以看出,当固定θ=1时,在不同步长序列{αn}下,算法均可以收敛到相同的稳定点p = 0. 987 8,其中αn= 0. 5/n时收敛速度最快;由图3可以看出,当固定αn=1/n时,算法在不同离散参数θ水平下均可以收敛到相应的稳定点,说明出行者对路网的熟悉程度并不会影响算法的收敛性.另外,对比图2和图3还可以看出,步长序列对于算法收敛性的影响要比离散参数的影响更加显著,选取合适的步长序列可以减少计算的迭代次数.
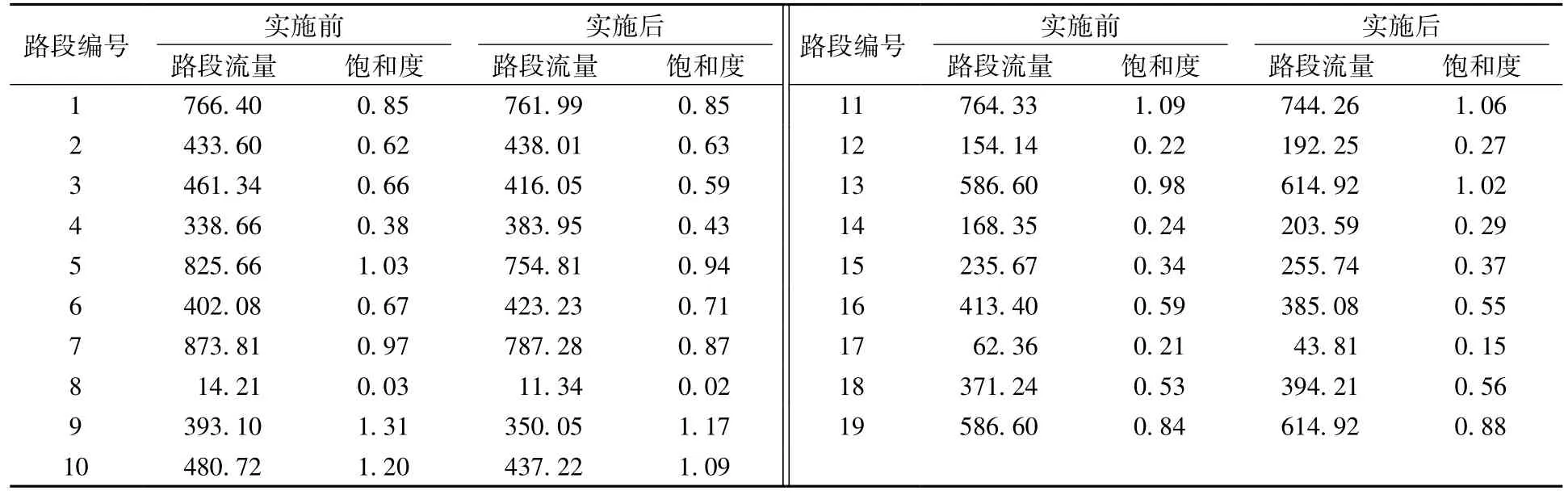
表2 路票策略实施前后的SUE路段流量对比

图2 不同步长序列{αn}下的收敛趋势

图3 不同离散参数θ下的收敛趋势
4 结语
本文主要研究了可交易路票策略下的随机用户均衡分配模型和算法.首先运用2个构造函数的相关性质建立了一个等价的通用型路票SUE模型,在Gumbel分布的感知误差假设下可得到Logit型路票SUE模型,并给出了路票价格唯一性的充分条件.其次提出一种高效且收敛的拉格朗日对偶算法,并通过算例说明该算法在不同情况下均具有较好收敛性.由于本文路票SUE模型明确考虑了出行者的随机感知误差,因此相对于路票UE模型来说可以更合理更准确地刻画出行者在给定路票策略下的路径选择行为.本文研究工作为城市交通拥堵治理提供一种新的思路和手段,并为可交易路票策略的定量评价和优化设计提供了理论基础.
参考文献(References)
[1]Yang H,Wang X L.Managing network mobility with tradable credits[J].Transportation Research Part B: Methodological,2011,45 (3 ) : 580-594.DOI: 10. 1016/j.trb.2010. 10. 002.
[2]Wang X L,Yang H,Zhu D L,et al.Tradable travel credits for congestion management with heterogeneous users[J].Transportation Research Part E: Logistics and Transportation Review,2012,48(2) : 426-437. DOI: 10. 1016/j.tre.2011. 10. 007.
[3]Zhu D L,Yang H,Li C M,et al.Properties of the multiclass traffic network equilibria under a tradable credit scheme[J].Transportation Science,2015,49 (3) : 519-534.
[4]Nie Y.Transaction costs and tradable mobility credits [J].Transportation Research Part B: Methodological,2012,46 (1 ) : 189-203.DOI: 10. 1016/j.trb.2011. 10. 002.
[5]He F,Yin Y F,Shirmohammadi N,et al.Tradable credit schemes on networks with mixed equilibrium behaviors[J].Transportation Research Part B: Methodological,2013,57(5) : 47-65.DOI: 10. 1016/j.trb.2013. 08. 016.
[6]Bao Y,Gao Z Y,Xu M,et al.Tradable credit scheme for mobility management considering travelers' loss aversion[J].Transportation Research Part E: Logistics and Transportation Review,2014,68: 138-154.DOI: 10. 1016/j.tre.2014. 05. 007.
[7]Meng Q,Lam W H K,Yang L.General stochastic user equilibrium traffic assignment problem with link capacity constraints[J].Journal of Advanced Transportation,2008,42(4) : 429-465.
[8]Maher M,Stewart K,Rosa A.Stochastic social optimum traffic assignment[J].Transportation Research Part B: Methodological,2005,39 (8) : 753-767.DOI: 10. 1016/j.trb.2004. 10. 001.
[9]Fisk C.Some developments in equilibrium traffic assignment[J].Transportation Research Part B: Methodological,1980,14(3) : 243-255.
[10]Larsson T,Patriksson M,Strömberg A B.Conditional subgradient optimization—theory and applications[J].European Journal of Operations Research,1996,88: 382-403.
[11]Sang N,Dupuis C.An efficient method for computing traffic equilibria in networks with asymmetric transportation costs[J].Transportation Science,1984,18 (2) : 185-202.
Stochastic user equilibrium model and its algorithm considering tradable credit scheme
Han Fei Cheng Lin
(School of Transportation,Southeast University,Nanjing 210096,China)
Abstract:In order to compensate the deficiency that the travelers are assumed to know the accurate route costs in previous credit equilibrium models,the stochastic user equilibrium (SUE) assignment with tradable credit scheme (TCS) was investigated.First,the equilibrium conditions of network flows and the credit market were presented to describe the equilibrium state of transportation network on a given TCS.Then an equivalent general SUE model with TCS was established based on the mathematical properties of two constructed functions.Under the assumption that travelers' perception errors are Gumbel distributed,the general SUE model with TCS was simplified to the Logit-based SUE model with TCS,and a sufficient condition for unique equilibrium credit price was provided.Since the traditional method of successive averaging (MSA) was not feasible,an efficiently convergent Lagrangian dual method (LDM) was proposed to solve the models.The numerical example results show that the LDM has good convergence on different step size sequences and dispersion parameters,and the step size sequences have a significant impact at the convergence speed than the dispersion parameters.
Key words:tradable credit scheme; stochastic user equilibrium; credit price;Lagrangian dual method
基金项目:国家自然科学基金资助项目(51178110,51378119)、江苏省研究生创新基金资助项目(KYLX 0178).
收稿日期:2015-07-05.
作者简介:韩飞(1986—),男,博士生;程琳(联系人),男,博士,教授,博士生导师,gist@ seu.edu.cn.
DOI:10.3969/j.issn.1001-0505.2016.01.035
中图分类号:U491
文献标志码:A
文章编号:1001-0505(2016) 01-0215-06
