重载铁路桥上反向曲线地段列车运行引起的动力响应分析及参数设置研究

时 瑾， 龙许友， 王英杰

(1. 北京交通大学 土木建筑工程学院， 北京 100044; 2.轨道工程北京市重点实验室， 北京 100044;3. 铁道第三勘察设计院集团有限公司，天津 300142)

近年来，我国相继建设的山西中南部、蒙西至华中地区铁路煤运通道设计初期即开行大轴重万吨及以上重载列车。重载铁路线路在山区线位受控因素增多，线路不得不在高架桥上设置曲线及反向曲线以适应地形，大轴重列车在桥上反向曲线上运行时可能对运行安全和桥梁结构产生不利影响。文献[1]规定，困难条件下，桥上反向曲线夹直线长度不能满足一个列车长度时，必须进行充分的技术经济论证并采取必要的技术措施，确保行车安全。

国内外学者对曲线地段重载列车与线路动力相互作用问题开展了大量研究。李伟等[2]采用NUCARS软件分析了曲线轨道参数对轮轨磨耗的影响；朱勇战[3]采用UM和ANSYS软件建立了列车与桥梁空间振动模型，检算了不同车辆通过反向曲线时动力学指标变化情况；宋郁民等[4]采用车桥耦合动力模型分析了小半径曲线上桥梁振动规律，据此研究了桥上曲线合理运行速度。现有研究主要集中在25 t及以下轴重货车与桥梁动力性能方面，桥上曲线设置对桥梁动力性能和大轴重货车运行安全性影响方面的关注较少。

本文以大轴重货车与桥梁动力模型为基础，对列车在桥上连续反向曲线地段运行时的动力响应进行检算，评估桥梁结构性能和运行安全性，讨论桥上曲线参数设置原则。

1 大轴重货车-曲线桥动力分析模型

1.1 动力分析模型建立

目前我国重载运输采用车型主要有C64、C70 、C80等[5]，轴重23 t或25 t。常用车辆一般采用转K6型转向架系铸钢三大件式货车结构。近年来，我国最新研制开发了30 t轴重C96型运煤专用敞车，其采用的DZ4型低动力交叉支撑转向架为下交叉支撑装置铸钢三大件货车转向架，轴箱一系弹性悬挂采用八字型弹性垫，二系为变摩擦减振装置弹簧悬挂系统，摇枕弹簧为两级刚度。

本文以三大件式货车结构为基础，结合大轴重货车特点建模。车辆各部件均视为刚体，车体和轮对均考虑沉浮、点头、横移、摇头和侧滚运动，侧架考虑沉浮、点头、横移、摇头和纵向运动，摇枕考虑摇头运动，一节货车总计51个自由度。各部件之间悬挂均考虑为线性弹簧阻尼元件。本文重点分析低频范围内车桥动力问题，理论模型忽略车辆非线性悬挂元件。

根据货车结构，对各部件进行受力分析[6]，见图1。图1中，Fzwl(r)i、Fywl(r)i、Fxwl(r)i分别为第i个轮对左(右)侧轮轨力的垂向、横向和纵向分量，Fzfl(r)i、Fyfl(r)i、Fxfl(r)i分别为第i个轮对左(右)侧一系悬挂垂向、横向和纵向力，Fztl(r)i、Fytl(r)i、Fxtl(r)i分别为第i个转向架左(右)侧二系悬挂垂向、横向和纵向力，Mztl(r)i为第i个摇枕左(右)侧摇头力矩。

结合受力分析结果，推导建立货车运动方程。将第i节车辆运动方程转换成矩阵形式

( 1 )

运动方程中荷载向量由两部分组成

( 2 )

式中：Fce、Fte、Fwe分别为作用于车体、转向架及轮对的重力、曲线引起的离心力；Fwn为由轮轨作用导致的法向力和蠕滑力。

曲线离心力对车辆部件的影响主要体现在沉浮、横移和摇头运动方程中，车体沉浮、横移和摇头运动方程中对应的曲线离心力分量表达式为

( 3 )

式中：mci为车体质量；Ici为车体摇头惯量；v为运行速度；Rc为车体中心处曲线半径；θs为车体中心处超高角。

桥梁建模采用模态综合技术，用ANSYS建立精细化有限元模型，求出结构自由振动的频率和振型，利用振型正交性，把互相耦联的数百个节点运动方程解耦，使其转化成为互相独立的模态方程[7]。

梁体任意横截面在3个方向的运动由振型函数的叠加表示为

( 4 )

第n阶桥梁模态方程成为

( 5 )

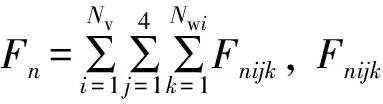
轮轨接触关系包括轮轨接触几何关系及轮轨相互作用力。将LM型车轮踏面与75 kg/m型钢轨断面匹配，组成一对轮轨关系，以轮对的横移量和摇头角为变量，计算轮轨空间接触迹线，得到相应轮轨接触几何参数。为方便使用，将计算结果列成数表存入计算机，进行计算时根据求得的轮对横移和摇头角，进行线性插值，得到计算不同时刻接触几何参数[8]。

采用经典的Kalker滚动接触理论计算蠕滑力。由于轮轨蠕滑力和法向力相互影响，求解时需迭代。由法向力确定接触斑参数，确定蠕滑系数和蠕滑力；由新得到的蠕滑力，结合轮对运动方程调整法向力；对比每次计算法向力增量，确定本时间步实际法向力[8]。

1.2 计算参数

车辆参数参考我国既有大轴重货车[9]，轴重按30 t考虑，货车轴距排列参考C96运煤敞车参数，见图2。

根据我国新建煤运通道设计速度，正线列车行车速度选取为120 km/h[10]。匀速运行条件下车钩不发生纵向冲动作用，编组数量对车辆安全性指标影响很小，可不考虑车间连接作用。根据车桥动力作用原理，当列车长度大于简支梁跨长时，编组数量对车桥横垂向动力响应影响不大，本计算列车长度选取6节编组，约84 m。

不同曲线半径对应不同超高值，根据重载曲线参数研究成果，为防止曲线磨耗，实设超高比均衡超高低10%～20%[11]。在我国重载既有线日常维护中，已实践证明采用欠超高设置能减轻轮轨磨耗。

轨道方向及高低不平顺均采用美国六级谱。计算长度根据线路方案确定，如线路长度4.536 km，计算时可设置140 孔32.4 m跨度桥梁。

以蒙西—华中铁路(简称蒙华铁路)32 m跨度桥梁设计方案为例，桥梁采用后张法预应力混凝土多片式T梁，单线采用两片梁，采用桥面板及横隔板连接成整体，梁横截面见图3。

根据截面尺寸建立梁有限元模型，进行自振分析，得到各阶频率及振型，表1为前10阶自振频率，图4为前4阶振型。计算可得一阶竖向频率4.57 Hz，二阶横向频率4.66 Hz，满足文献[12]竖向自振频率23.58L-0.592 8=3.03 Hz(L为跨度)、横向自振频率60/L0.8=3.75 Hz的控制下限值。本设计梁横向频率高于目前既有重载铁路相同类型桥梁(朔黄铁路32 m梁横向自振频率约4.08 Hz)，横向刚度提高对改善车桥横向振动性能有利。

表1 32 m跨度梁前10阶模态

模态阶数固有频率/Hz振型特征模态阶数固有频率/Hz振型特征14．5742竖向弯曲，半波24．6602横向弯曲，半波39．4265局部变形412．0910扭转变形，半波514．3460竖向弯曲，整波618．8870扭转，半波720．9100竖向弯曲，整波823．2000扭转，整波928．6190扭转，2个整波1032．3380局部变形

选取模态分析得到的前10阶振型和频率，为式( 4 )桥梁振动方程提供模态信息。根据文献[7]建议，对跨度大于20 m的预应力混凝土梁，阻尼比选取0.01。

1.3 程序编制及结果验证

结合上述理论，开发重载桥上曲线动力学检算程序HHRDYNA(Dynamic Analysis Program of Train and Bridge on Heavy Haul Railway Curve)，程序总体设计框架见图5。

程序中对列车-曲线桥系统振动方程联立求解，采用以轮轨力为纽带的交叉迭代数值算法，对列车和桥梁2个子系统方程通过Newmark-β积分格式求解，在每一时间步利用轮轨力实现列车系统与桥梁系统之间交叉迭代，通过构造梁体变形收敛性准则控制迭代逼近程度，实现每一时间步动力响应求解。

2014年12月，笔者在山西中南部铁路试验段(长子南-平顺)进行了30 t大轴重列车运行试验，以其测试结果为基础进行模型验证。测试工点位于K587+851处，桥上曲线半径800 m，圆曲线长1 238.88 m，缓和曲线长200 m，实设超高90 mm。试验列车编组为HXD1机车(1台)+WX检测车(1辆) + C96货车(66辆)+ HXD2机车(1台)，牵引质量80 000 kg，运行速度87 km/h，其中C96货车满载轴重为30 t。

在圆曲线中点布置测点，分别测试轨道横向力、垂向力和桥梁跨中横向振动加速度、横向振幅、垂向加速度、垂向振幅等。

结合桥梁振动响应测试结果，采用余振法求得32 m跨度桥梁一阶垂向自振频率为5.31 Hz，一阶横向自振频率5.47 Hz。

表2为试验列车中C96货车通过时各项动力学指标实测最大值和计算最大值，图6为内外轨横向力实测值与计算值上下限的偏离程度。对比可见，计算结果和测试结果总体上吻合良好。造成对比结果差异的原因主要是计算中轨道不平顺不是现场实测数据及动力学模型忽略了道砟体系参振。本文理论模型能够较好反映重载列车在桥上曲线地段运行时的车桥动力相互作用特性，能够满足工程应用要求。

表2 C96货车通过时动力学指标实测值和计算值对比

指标实测值计算值外轨脱轨系数0．1120．176内轨脱轨系数0．1210．162外轨横向力/kN28．24528．121内轨横向力/kN25．35925．238外轨轮重减载率0．1090．123内轨轮重减载率0．2650．100桥梁跨中横向振幅/mm0．1710．202

2 重载铁路曲线参数设置要求

夹直线长度的设置主要考虑线路养护要求和行车平稳要求。根据文献[13]，一般路基地段圆曲线间夹直线最小长度取0.6v；对于桥上曲线设置问题，列车曲线通过时的离心力作用会加剧车桥振动，有可能会对运行安全和线路稳定造成不利影响，因此桥上不宜设置反向曲线，如果不得已而设置反向曲线时，应尽可能选取较长的夹直线。

对于最小曲线半径选取，文献[13]基于轮轨磨耗、安全性综合考虑确定。对重载铁路，最小曲线半径采用欠超高不大于容许值和磨耗条件确定，满足最高行车速度要求的最小曲线半径计算式为

( 6 )

式中：hmax为实设超高最大值;hqy为欠超高容许值。

对于按120 km/h速度设计的重载铁路，按实设超高最大值150 mm，欠超高容许值取70 mm(一般)和90 mm(困难)，计算得到最小曲线半径为772 m(一般)和708 m(困难)。

内外轨均磨条件的曲线半径计算式

( 7 )

式中：vj为均磨速度，取0.8vmax。

求得最小曲线半径为724 m。

综上，确定重载铁路最小曲线半径为800 m。从实际观测看，进一步降低曲线半径将导致钢轨磨耗量快速增长，如大秦线800 m半径曲线钢轨每年换轨1次，500 m半径曲线钢轨每季度换轨1次。

文献[13]中夹直线和最小曲线半径的确定未考虑具体线路结构。重载铁路通过困难山区时不得不在桥上采用连续曲线以满足线位控制要求。大轴重条件下桥上连续设置曲线或采用曲线参数下限值是否会对运行安全性和结构服役性能造成不利影响，需进一步通过车桥动力分析确定。

3 典型区段动力响应分析

以蒙西至华中铁路浩勒报吉至三门峡段新家坪跨牡丹川1号大桥反向曲线为计算对象。该段曲线由1 000 m和800 m半径曲线组成，见图7。其中，1 000 m半径曲线实设超高140 mm，800 m 半径曲线实设超高150 mm。

对这段曲线进行动力学检算，列车运行方向及轨道左右侧关系见图8，系统动力性能控制指标见表。为典型动力响应时程曲线，动力学指标最大值统计结果见表3所示。

表3 动力性能控制指标

表4 动力学指标峰值

评价指标曲线1夹直线曲线2左侧右侧左侧右侧左侧右侧车体垂向加速度/(m·s-2)1．2850．7311．273车体横向加速度/(m·s-2)0．5560．4060．863轮轨横向力/kN27．45222．45824．70023．59221．55629．990轮轴横向力/kN16．9289．53820．809轮轨垂向力/kN164．102158．674158．894159．716152．761174．264轮重减载率0．0690．1350．0760．0880．1550．061脱轨系数0．1740．1500．1280．1240．1450．182梁跨中垂向位移/mm17．8717．5118．24梁跨中垂向加速度/(m·s-2)0．8160．4691．324梁跨中横向位移/mm0．4100．2340．967梁跨中横向加速度/(m·s-2)0．1580．2030．228

计算表明：

(1) 列车通过2个反向曲线时，车体最大垂向加速度1.29 m/s2，未被平衡的最大横向加速度0.86 m/s2，满足列车运行舒适性标准要求；

(2) 反向曲线地段轮轨横向力最大值30 kN，轮轴横向力最大值20.8 kN，脱轨系数最大值0.18，轮轨垂向力最大值174.3 kN，轮重减载率最大值0.16，各项安全性指标均小于安全限值；

(3) 曲线上桥梁横向位移明显增大，特别是800 m半径曲线上梁的跨中横向位移达到最大值。桥梁跨中最大垂向加速度1.32 m/s2，桥梁跨中横向最大振动加速度0.23 m/s2，各项指标满足桥梁动力性能控制限值。

(4) 800 m半径曲线上安全性指标显著提高，如轮重减载率比1 000 m半径曲线提高约15%，梁跨中横向变形增加约135%。

4 桥上曲线参数设置分析

4.1 反向曲线夹直线长度分析

为突出重载铁路桥上曲线线形对行车性能影响，本节不考虑轨道不平顺，分析桥上夹直线长度设置问题。

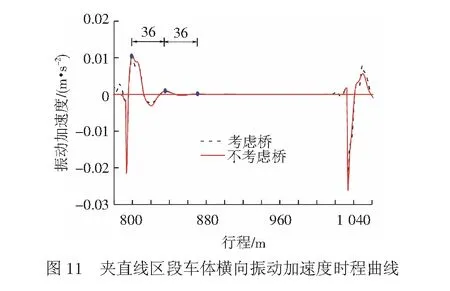
文献[13]中夹直线长度是根据振动衰减来确定的，本节在2个800 m反向曲线间设置240 m长夹直线。图10为考虑桥和不考虑桥条件下反向曲线地段车体横向振动加速度变化情况。由图10可见，由于曲线离心力作用引起车桥横向动力作用加剧，在桥上曲线运行时车辆横向加速度不会出现明显衰减；在夹直线段由于离心力消失，车辆横向加速度迅速衰减。图11为考虑桥和不考虑桥情况下夹直线地段车辆横向振动加速度峰值衰减情况。由图11可见，桥梁结构性能对夹直线上车辆横向振动影响很小，缓直点引起的冲击响应在2个振动周期(约72 m)内基本可衰减完成，无论反向曲线设置在桥上还是一般路基地段，夹直线长度均可按0.6v的长度设计。

4.2 不同工况桥上反向曲线设置统计分析

浩勒报吉至三门峡段位于蒙华铁路北段，全长约645 km。该区段地形复杂，有15处地段桥上设置了反向曲线，部分地段曲线用到了文献[12]推荐的800 m最小半径，大部分夹直线设置受地形影响，长度均短于一列车长，具体曲线参数设置见表5。

对各线路条件下车桥动力响应进行计算，统计得到不同半径下关键动力学指标变化规律，总体评估桥上曲线设置合理性。图12为设计速度120 km/h条件下不同半径曲线轮轴横向力、桥梁跨中横向位移、轮重减载率和脱轨系数变化曲线。由图12可见，曲线半径大于1 000 m时，各项动力学指标变化平缓，基本维持在较低水平；800 m半径曲线上动力学指标较1 000 m半径时有所提高，总体上都能较好满足车桥动力性能控制标准。

表5 蒙华铁路15个典型桥上连续反向曲线工况

工况曲线半径/m超高/mm夹直线长/m缓和曲线长/m112001200120120240．0614012021200160012090224．4812012031200160012090344．63120120410001400140100214．80160905100080014015083．6316018068001200150120299．21180140712001000120140155．881401108100012001200140120120115．13102．2716012012091200140012010092．58100110101200160012090172．311201201112001300800120110150413．91399．62120140180128008001400150150100165．91683．00200180100138001400150100316．43200701412002000800120012070150120955．31321．28153．3214070200120151000100014014093．48140160

5 结论

本文结合大轴重货车-曲线动力分析模型，对30 t轴重列车通过桥上连续反向曲线时列车与桥梁结构的安全性及动力性能进行了研究，对设计速度目标值120 km/h重载铁路桥上曲线设置问题得出以下主要结论：

(1) 夹直线长度不是影响行车动力学指标的主要因素。列车行径夹直线区段时，缓直点引起的车体振动响应在2个振动周期(约72 m)内基本可衰减完成，桥上反向曲线间夹直线长度可按0.6v的长度设计。

(2) 曲线半径是影响桥上反向曲线地段运行安全性和结构动力性能的主要因素。当曲线半径大于800 m时，各项动力学指标均能满足车桥动力性能控制标准。曲线半径大于1 000 m时，各项动力学指标变化趋缓。设计中推荐桥上采用1 000 m以上曲线半径，困难条件下桥上最小曲线半径可采用800 m。

参考文献：

[1] 中国铁路总公司. TB 10002.1—2005《铁路桥涵设计基本规范》局部修订条文[Z].北京：中国铁路总公司，2013.

[2] 李伟，马战国，司道林. 重载铁路曲线几何参数对钢轨磨耗影响的研究[J]. 铁道建筑，2013(6):130-134.

LI Wei, MA Zhanguo,SI Daolin. Study on the Influence of Curve Geometric Parameters of Heavy Haul Railway on Rail Wear [J]. Railway Engineering，2013(6):130-134.

[3] 朱勇战. 反曲线铁路桥梁空间车桥耦合动力分析[J]. 重庆理工大学学报(自然科学版)，2013,27(6): 17-22.

ZHUYongzhan.Studies on Space Coupling Dynamic Responses of Vehicle and Anti-curve Bridge System[J].Journal of Chongqing Institute of Technology ：Natural Science，2013，27(6): 17-22.

[4] 宋郁民，吴定俊，侯永姣. 列车通过小半径反向曲线桥梁的动力相互作用分析[J]. 工程力学，2012，29(S1): 185-189.

SONG Yumin,WU Dingjun,HOU Yongjiao. Analysis of Dynamics Interaction about Train Curving Bridge on Small Radius and Reverse Curve[J]. Engineering Mechanics，2012，29(S1): 185-189.

[5] 耿志修. 大秦铁路重载运输技术[J]. 铁道知识，2009(3): 4-9.

[6] 翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2014.

[7] 夏禾，张楠. 车辆与结构动力相互作用[M]. 北京：科学出版社, 2005.

[8] 龙许友，时瑾，王英杰，等. 高速铁路线路线形动力仿真及乘坐舒适度评价[J]. 铁道科学与工程学报，2012, 9(3): 26-33.

LONG Xuyou,SHI Jin,WANG Yingjie. Dynamic Simulation and Ride Comfort Evaluation of Track Alignment for High Speed Railway[J].Journal of Railway Science and Engineering，2012,9(3): 26-33.

[9] 薛继连. 朔黄重载铁路轮轨关系[M].北京：中国铁道出版社, 2013.

[10] 李洪斌. 张唐重载铁路主要技术标准研究[J]. 铁道标准设计，2011(7): 5-9.

LI Hongbin.Discussion on Main Technical Standards for Zhangjiakou-Tangshan Heavy Haul Railway[J]. Railway Standard Design， 2011(7): 5-9.

[11] 孟宪洪. 重载铁路小半径曲线钢轨减磨措施试验研究[J]. 中国铁路，2013(5): 37-41.

MENG Xianhong.Experimental Study on the Reduction of Heavy Haul Railway Wear of the Small Radius Curve [J]. Chinese Railways， 2013(5): 37-41.

[12] 中华人民共和国铁道部. 重载铁路设计规范(送审稿)[Z]. 北京：中国铁道出版社，2011.

[13] 中华人民共和国铁道部. GB50090—2006 铁路线路设计规范[S]. 北京：中国计划出版社，2006.

[14] 中华人民共和国铁道部. GB5599—85 铁道车辆动力学性能评定和试验鉴定规范[S]. 北京: 中国铁道出版社, 1985.

[15] 铁道部科学研究院机车车辆研究所. 95J01-L 高速试验列车动力车强度及动力学性能规范[Z]. 北京: 中国铁道出版社, 1995.

[16] 中华人民共和国铁道部. 铁运函[2004]120 铁路桥梁检定规范[S]. 北京: 中国铁道出版社, 2004.