高速列车锻钢制动盘多裂纹间作用机制研究
2016-05-09石晓玲赵方伟
石晓玲, 李 强, 薛 海, 赵方伟
(北京交通大学 机械与电子控制工程学院, 北京 100044)
热疲劳作为高速列车制动盘失效的关键因素之一,直接影响高速列车的运行安全。观察大量失效制动盘的裂纹发现,制动盘表面存在多条裂纹,且错综复杂,见图1。通常裂纹间的相互作用影响裂纹尖端的应力场分布和裂纹扩展规律,但目前对制动盘裂纹的研究多以单条裂纹为主[1-3],对多裂纹的扩展规律研究较少。因此,开展高速列车锻钢制动盘多裂纹间的作用机制研究具有实际的工程意义和学术价值。
针对多裂纹间相互作用问题,国内外学者采用数值模拟和试验等方法进行了相关研究。Nicolas Malesys等[4]提出了热疲劳载荷下裂纹网形成和扩展的概率模型,为裂纹网屏蔽效应的研究提供了参考;K C Wu等[5]采用位错理论研究了多条平行裂纹在非平面动态载荷下的屏蔽规律;Li等[6]利用修正的Kachanov模型研究了不同裂纹系之间的相互作用;Basista等[7]结合Kachanov模型分析了脆性材料在均布压应力作用下二维裂纹间的相互作用;Fletcher等[8]研究了相邻长裂纹(几十毫米)在弯曲载荷下的相互作用,结合单条裂纹的应力强度因子(ΔK)预测了裂纹的扩展;黄明利等[9]通过对有机玻璃材料进行单轴加载试验,研究发现裂纹间的相互作用主要通过空间位置对裂纹扩展起促进和抑制作用;闫明等[10]人研究了热疲劳裂纹网的屏蔽规律,并利用该屏蔽规律提出了裂纹网中主裂纹应力强度因子的计算方法;李伟等[11]人研究发现钢轨上裂纹数量大于5 条时可以反应多裂纹扩展特性的影响。
虽然目前对多裂纹间作用机制的研究已取得了较多成果,但这些研究主要以二维裂纹为主。本文通过对高速列车锻钢制动盘进行1∶1台架试验,分析了盘面三维裂纹的长度变化,并基于有限元法研究了不同深长比、裂纹空间位置及裂纹数量下,盘面裂纹间的作用机制,研究成果可以为盘面裂纹的剩余寿命和裂纹容限的制定提供参考。

1 制动盘热疲劳试验
文献[12-13]指出裂纹萌生寿命大约占总扩展寿命的2/3,为缩短试验时间,节省试验经费,取正在服役中且盘面已存在裂纹的制动盘为试验对象。在铁道部工务器材厂进行1∶1制动台架试验。为确保试验结果可以真实的反映制动盘的实际工作性能,试验参数与实际运行过程中基本相同[14]。
目前1∶1台架试验的最高速度为220 km/h,所以本次试验初速度取200 km/h,制动时间为44 s,初始制动压力为18.39 kN,并随着速度的减小不断增大,制动结束时的压力为34.63 kN。试验前对制动盘进行118 km/h的低速磨合。制动工况为3次连续200 km/h紧急制动,每次制动结束后冷却到50 ℃左右,人工跟踪测量裂纹长度变化。试验过程中共进行849 次紧急制动,试验结束后盘面裂纹有明显扩展。



在制动盘盘面选取15条较长裂纹,分别用A1~A15表示,见图2。图3(a)、图3(b)分别为不同制动次数后,A4、A8裂纹的长度变化(A4和A8在图中用箭头标注)。图4为裂纹长度随制动次数的变化曲线。考虑到盘面裂纹比较复杂,每次制动结束后测量值存在一定的人工误差,因此,图4中裂纹长度曲线在制动过程中有一定的波动。观察图3、图4发现,制动盘盘面裂纹主要以径向裂纹为主;A3、A4、A7、A8、A11、A15裂纹长度变化比较明显,主要是由于制动过程中伴随着裂纹的自身扩展,2条相近裂纹连通成为一条长裂纹形成的;A1、A2、A5、A6、A9、A10、A12、A14裂纹长度略有增加,但并不明显;由于A13测量数据较少,图4中未列出该裂纹的长度曲线;随着制动次数的不断增加,盘面未跟踪记录的裂纹也稍有扩展。
2 数值计算模型
2.1 制动盘载荷分析
在制动过程中,制动盘所受的力主要有惯性力、闸片对制动盘摩擦面的垂直压力、闸片对制动盘摩擦面的切向摩擦力、摩擦产生的热应力等。文献[12]证明制动过程中的热应力是制动盘产生疲劳裂纹的主要因素,因此本文主要研究热应力下裂纹间的作用机制。
列车制动过程是通过闸片和制动盘摩擦将列车的动能转化为热能的过程。但闸片导热性较差,制动过程中的能量主要被制动盘吸收,为了简化计算,采用摩擦功率法[12]计算摩擦面上的热流密度
q(r,t)=ηfsp0ω(t)r
( 1 )

2.2 有限元模型
本文仿真工况与1∶1台架试验工况完全相同,采用ANSYS有限元软件模拟3 次200 km/h连续紧急制动下的瞬态温度场和应力场分布。为了研究热应力作用下盘面裂纹间的作用机制,基于子模型法和三维裂纹扩展软件FRANC3D[15]建立含裂纹的有限元模型,见图5。

为了适应裂纹尖端应力场的奇异性,裂纹前缘采用8 个15 节点楔形单元,楔形单元周围生成2 层20 节点的六面体单元环,其余区域使用10节点的四面体单元组成,四面体单元和六面体单元之间采用13节点的金字塔形单元过渡。裂纹尖端的单元关于裂纹面对称和反对称,不仅消除了裂纹面带来的离散误差,而且提高了计算精度。
制动盘裂纹剖面的形状特征表明,盘面裂纹为表面半椭圆型裂纹[16]。裂纹扩展过程中深长比a/2c是变化的,因此分别研究深长比为0.1、0.2、0.5时,裂纹间的相互作用。为了简化计算,模型中主裂纹设为径向裂纹,长度为20 mm,副裂纹设为径向或周向裂纹,长度为5 mm。
3 有限元结果分析
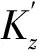
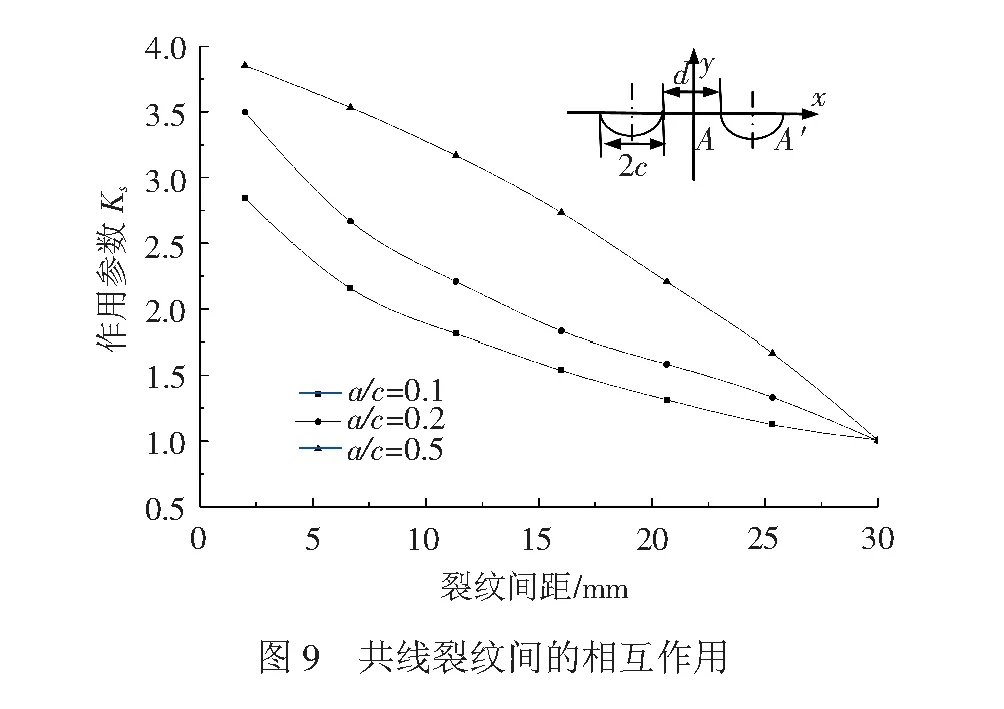
( 2 )
式中:Ks=1表示裂纹间不存在相互作用;Ks<1表示裂纹之间的屏蔽作用较强,可有效抑制裂纹的扩展;Ks>1表示裂纹之间的增强作用较强,可有效促进裂纹的扩展。
研究制动盘盘面裂纹的分布形式发现,裂纹之间的空间位置有3 种基本形式:平行裂纹、共线裂纹和交叉裂纹。分析中设定长裂纹为主裂纹,沿制动盘径向方向,其他短裂纹设定为副裂纹,分别研究这3 种形式下裂纹间的作用机制。
3.1 平行裂纹的作用机制

为研究多条平行裂纹间的作用机制,分别计算多条径向裂纹相互作用时的应力强度因子。图6为深长比a/2c为0.2,副裂纹数N从0~8时主裂纹前缘的应力强度因子。横轴的“0”和“1”分别表示裂纹尖端的2 个表面点,“0.5”为裂纹的中心位置(下同)。由图6可知,副裂纹数N为2、4、6、8条时主裂纹的应力强度因子减小率分别为2.7%、7%、14.3%、46.6%,由此可见副裂纹数越多,主裂纹的应力强度因子越小,裂纹扩展速率越低,该结论与1∶1台架试验中裂纹A1、A2、A5、A6、A9、A10、A12、A14的扩展规律基本一致。当N=8时,主裂纹前缘的应力强度因子逐渐接近于裂纹扩展的门槛值,因此副裂纹数大于8 条时可以反映多条平行裂纹的扩展特性。
图7为副裂纹数N=6时,不同深长比下主、副裂纹间距d与主裂纹尖端表面A点的作用参数变化规律。研究发现,裂纹间距越小,深长比越小,主、副裂纹的相互作用越明显。当a/2c=0.1或0.2时,作用参数Ks<1,裂纹间相互抑制。当a/2c=0.5时,作用参数Ks>1,裂纹间相互促进。

3.2 共线裂纹的作用机制
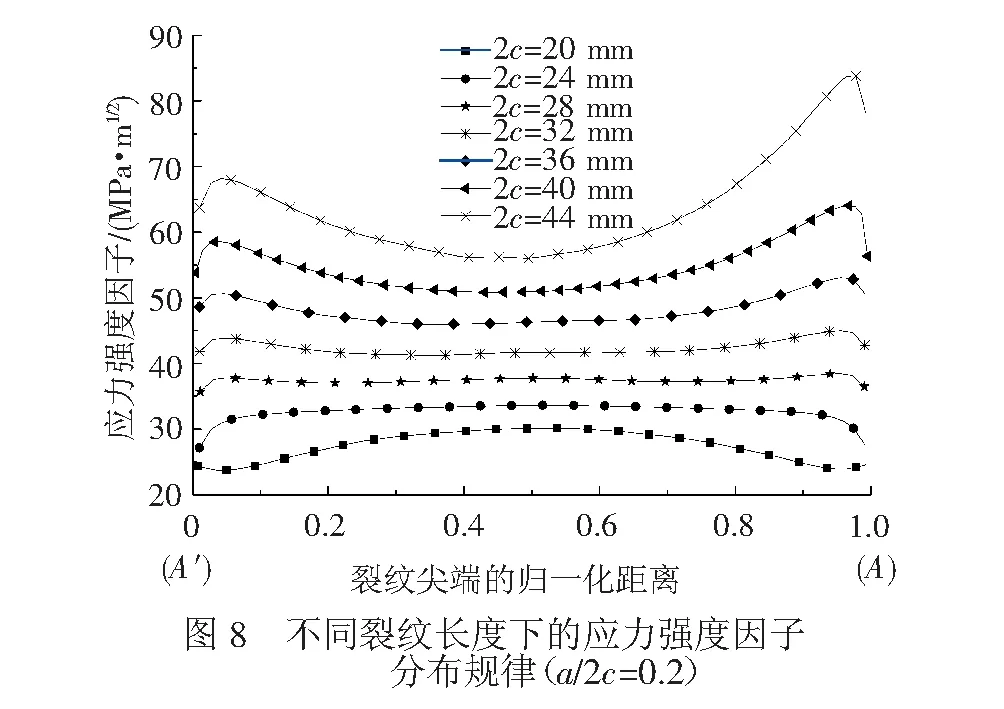
图8为初始裂纹长度2c=20 mm,初始间距d=30 mm,深长比a/2c=0.2时,同一截面上2 条长度相等、共线径向裂纹的应力强度因子分布规律。由图可知,随着裂纹长度的不断增加,相邻裂纹间距逐渐减小,裂纹尖端的应力强度因子逐渐增大,但A点的应力强度因子增加速度明显高于A′点,故裂纹扩展过程中随着d的不断减小,2共线裂纹容易连通成一条长裂纹,在一定程度上加速了疲劳破坏问题,该结论与1∶1台架试验中裂纹A3、A4、A7、A8、A11、A15的扩展规律基本一致。当d=2 mm时,A点的应力强度因子逐渐接近于制动盘材料的断裂韧性,进入失稳扩展阶段。
图9为不同深长比下,裂纹尖端距离d与裂纹前缘表面A点作用参数的变化规律。由图可知,共线裂纹间的相互作用会促进裂纹的扩展;裂纹间距d不变时,a/2c越大,作用参数Ks越大,裂纹间的相互促进作用越强;裂纹间距d越小,作用参数Ks也越强。
3.3 交叉裂纹的作用机制
空间交叉裂纹中主裂纹设为径向裂纹、副裂纹设为周向裂纹,计算深长比a/2c=0.2,裂纹间夹角θ=90°的应力强度因子。计算结果表明主裂纹前缘的应力强度因子基本不变,副裂纹前缘的应力强度因子变化比较明显,见图10。由图10可知,随着裂纹间距d不断减小,副裂纹前缘表面B点的应力强度因子先增大后减小,B′的应力强度因子不断增大。当d=10 mm时,副裂纹前缘表面B点的应力强度因子逐渐接近于0 MPa·m1/2,因此周向裂纹基本不会影响径向裂纹的扩展特性。

图11为不同裂纹深长比下,裂纹间作用参数随裂纹间距d的变化规律。由图可知,主裂纹表面A点的作用参数Ks基本不随裂纹间距d的变化而变化。但副裂纹表面B点的作用参数Ks与裂纹间距d密切相关。裂纹深长比越大,裂纹间的作用参数Ks越大。裂纹间距d<12 mm时,作用参数Ks<1,裂纹间的相互作用抑制了副裂纹的扩展;当裂纹间距12 mm

4 结论
制动盘裂纹属于典型的热疲劳裂纹,本文通过1∶1台架试验和有限元计算相结合的方法,研究了多条裂纹不同形状比下的应力强度因子和裂纹间作用机制规律。具体结论如下:
(1) 1∶1台架试验结果表明盘面以径向裂纹为主。裂纹扩展有2 种途径:裂纹自身扩展和多条裂纹连通扩展。裂纹数量越多,盘面裂纹扩展越慢,有效的延缓了制动盘的疲劳破坏。
(2) 平行径向裂纹数量越多,主裂纹的应力强度因子越小,裂纹扩展速率越低。主、副裂纹的相互作用随裂纹间距和深长比的变化而变化。
(3) 共线径向裂纹间距越小,深长比越大,裂纹前缘的应力强度因子越大,裂纹间越容易连通成一条长裂纹,在一定程度上促进了裂纹的扩展。
(4) 径向裂纹对周向裂纹扩展的影响较小,但周向裂纹表面点的作用参数随裂纹间距和深长比的变化而变化。
参考文献:
[1] HOAI N L, GARDIN C. Analytical Prediction of Crack Propagation Under Thermal Cyclic Loading Inducing a Thermal Gradient in the Specimen Thickness-comparison With Experiments and Numerical Approach[J].Engineering Fracture Mechanics, 2011,78(4):638-652.
[2] MAHMUT U, OGUZHAN D, ALI O, et al. Surface Cracks in Finite Thickness Plates Under Thermal and Displacement-controlled Loads—Parts 1: Stress Intensity Factors[J]. Engineering Fracture Mechnics,2014,115:284-295.
[3] MAHMUT U, OGUZHAN D, ALI O, et al. Surface Cracks in Finite Thickness Plates Under Thermal and Displacement-controlled Loads—Parts 2: Crack Propagation[J]. Engineering Fracture Mechnics,2014,115:255-269.
[4] Nicolas Malésys, Ludovic Vincent, Francois Hild. A Probabilistic Model to Formation and Propagation of Crack Networks in Thermal Fatigue[J]. International Journal of Fatigue,2009,31(3):565-574.
[5] WU K C, HOU Y L, HUANG S M. Transient Analysis of Multiple Parallel Cracks Under Anti-plane Dynamic Loading[J].Mechanics of Materials, 2015,81:56-61.
[6] LI Y P, THAM L G, WANG Y H, et al. A Modified Kachanov Method for Analysis of Solids with Multiple Cracks[J]. Engineering Fracture Mechnaics,2003,70(9):1 115-1 129.
[7] BASISTA M, GROSS D. A Note on Crack Interactions Under Compression[J]. International Journal of Fracture,2000,102(3): 67-72.
[8] FLETCHER D I, HYDE P, KAPOOR A. Growth of Multiple Rolling Contact Fatigue Cracks Driven by Rail Bending Modeled Using a Boundary Element Technique[J]. Proceedings of Institution of Mechanical Engineers Part F: Journal of Rail and Rapid Transit, 2004,218(3):243-253.
[9] 黄明利,黄凯珠.三维表面裂纹相互作用扩展贯通机制试验研究[J].岩石力学与工程学报,2007,26(9):1 794-1 799.
HUANG Mingli, HUANG Kaizhu. Experimental Study on Propagation and Coalescence Mechanisms of 3D Surface Cracks[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(9):1 794-1 799.
[10] 闫明,王世杰,孙淑霞,等. 热疲劳裂纹网的屏蔽规律及主裂纹应力强度因子的计算方法[J].机械工程学报,2009,45(12):279-283.
YAN Ming, WANG Shijie, SUN Shuxia, et al. Shielding Effect Rule of Thermal Fatigue Crack Net and Calculating Method of Stress Intensity Factor of Main Crack[J]. Journal of Mechanical Engineering,2009,45(12):279-283.
[11] 李伟,温泽峰,金学松,等. 轮轨摩擦接触下钢轨多裂纹相互作用研究[J].工程力学,2012,29(11):295-301.
LI Wei, WEN Zefeng, JIN Xuesong, et al. A Study of Multiple Crack Interaction of Rail Under Wheel-rail Friction Contact[J]. Engineering Mechanics,2012,29(11):295-301.
[12] 杨月.高速列车SiCp/A356复合材料制动盘热疲劳评价方法研究[D]. 北京:北京交通大学,2008:34-37.
[13] 周素霞,谢基龙. 高速客车空心车轴裂纹扩展特性研究[J].工程力学,2009,26(7):232-237.
ZHOU Suxia, XIE Jilong. Research of the Fatigue Crack Propagation Characteristic on Railway Hollow Axles[J]. Engineering Mechanics,2009,26(7): 232-237.
[14] 李森林. 1∶1列车制动试验台测控系统的设计开发[D]. 成都:西南交通大学,2009:10-12.
[15] YAN Xiangqiao, LIU Baoliang. A Numerical Analysis for Cracks Emanating from a Surface Semispherical Cavity in an Infinite Elastic Body by FRANC3D[J].Engineering Failure Analysis,2008,15(1-2):188-192.
[16] YANG Zhiyong, HAN Jianming, LI Weijing, et al. Analyzing the Mechanisms of Fatigue Crack Initiation and Propagation in CRH EMU Brake Discs[J].Engineering Failure Analysis, 2013,34:121-128.
