动车所通过能力计算模型与方法研究

陈 韬， 吕红霞， 潘金山， 赵敬勇

(1. 西南交通大学 交通运输与物流学院， 四川 成都 610031；2. 西南交通大学 全国铁路列车运行图编制研发培训中心， 四川 成都 610031；3. 西南交通大学 综合交通运输智能化国家地方工程联合实验室， 四川 成都 610031；4. 济南铁路局 济西站，山东 济南 250117)

动车所承担动车组除高级检修以外的全部维修工作以及动车组存车作业，一般设置在高铁线路始发站、终到站、枢纽站附近，是保证动车组具有安全正常运用状态的维修整备场所。相对于不断出入的动车组，动车运用所的检修设备能力相对稀缺。因此，限制了给定时段内动车所通过或接发的动车组数量。动车所在给定时段内，一定设备条件和作业方式下，能整备的最大动车数量即为动车所通过能力。正确计算动车所通过能力对挖掘动车所作业能力、协调高铁路网点线能力有重要意义。

目前，动车所通过能力计算的相关研究较少，大部分研究主要集中在普速车站客车整备所通过能力计算、高铁客运站通过能力计算、动车所调车作业计划编制问题上。普速车站客车整备所通过能力目前仍然采用传统的利用率法进行计算，限于各种参数取值的影响，计算结果准确度不高[1]；高铁客运站需要准确计算不同时段的通过能力，国内外学者都致力于运用基于各种智能算法的模拟仿真法进行计算，得到较好的效果，但动车所作业组织复杂性、灵活性比高铁客运站高，这些理论方法可以借鉴但还不能直接运用[2-3]；李波[4]给出单个环节的动车所检修设备能力测试公式，并给定反应检修效果的系数范围，但是没有考虑检修作业间相互影响下的检修能力；耿敬春等[5]以北京动车段为例，通过比较分析列车运行图不同时段下出入段动车组数与最小追踪间隔下出入段动车组数的关系，提出出入段能力的适应性和加强措施，但没有探讨动车所能力的计算方法；林伯梁[6]、李建等[7]研究动车组一级检修调车作业计划自动编制问题，根据人工编图经验设计启发式规则，开发相关信息系统；王忠凯等[8]对动车组调车作业计划编制问题建立以核心作业时间延误最小为目标的数学模型，并运用最大最小蚁群算法进行模型求解，没有涉及动车所通过能力计算。

模拟仿真法已被证明是计算通过能力的有效方法，通过多次模拟动车所作业过程可以较为精确的确定动车组整备的最大数量[2-3]。而模拟仿真的关键是要确定有效的智能搜索算法，确保在可接受资源消耗内找到理想解。本文在前人研究基础上，分析动车所通过能力的影响因素，建立动车所通过能力计算的0-1规划模型，并运用启发式排序规则与基于最长活动链的混合邻域禁忌搜索算法进行求解，为模拟仿真计算动车所通过能力提供可行的思路。

1 问题分析

动车所通过能力影响因素主要可分为3类:

(1) 动车所各类检修设备、各场库股道设备以及连接各场库的咽喉道岔设备，包括站型、股道、咽喉、信号、检修库、洗车库、吸污设备等。因此，动车所通过能力从设备上又可分为检修设备能力、场库股道通过能力及咽喉道岔通过能力3种，动车所通过能力不能简单的等同于某一类设备的通过能力，而应该是这几类设备协调配合所体现出的整体通过能力。

(2) 保证行车安全和作业质量的各种作业规则和标准，包括行车间隔标准(列车到达追踪间隔、出发追踪间隔、不同时到发间隔等)、动车组检修作业时间标准(洗车作业时间、卸污作业时间、检修库检修作业时间等)、动车组走行作业时间标准(动车组在各场库间的转线作业时间)，动车组检修作业流程(存车作业流程、一级检修作业流程、二级检修作业流程等)、动车组调车作业流程等。这些作业规则和标准规定动车所设备使用的时间和频率，从效率上影响动车所通过能力。

(3) 动车所技术作业方案。动车所技术作业是对动车所能力的直接利用，包括动车组检修计划、动车组运用计划和动车组调车作业计划。其中，动车组检修和运用计划是根据动车交路计划及动车组使用状态确定的本动车所配属动车组的日常检修及分配计划，也就是动车所的整备作业任务，包括不同检修动车组的数量、比例、出入动车所先后顺序及时间等。动车组调车作业计划是根据动车组检修和运用计划编制的动车组在动车所内各场库的股道停留和转线计划，涵盖动车组的进所、检修、存车和出所的全过程，是保证动车所整备作业任务能够完成的设备运用计划，包括动车组在动车所的出入所进路、各场库股道运用顺序、占用起止时间，转线进路及时间等方案[8]。

动车组调车作业计划是动车组检修作业任务与车站设备能力相适应的关键环节，方案的优劣对动车所能力的利用程度有直接影响。相同的检修和运用计划，动车组调车作业计划方案较优时，给定时段内对动车所设备能力占用少，可安排更多的检修任务。图1、图2为某动车所8:00～13:00间的2个不同调车作业方案，图1只能安排整备4列动车组，图2将图1中U3的最后1项存车线上的整备作业更换1条股道(如图2上虚横线所示)则可以安排整备5列动车组。由此可知，假设给定时段内检修和运用计划的动车组数为Z，如果按最优方案安排其调车作业后，无法再增加动车组，则Z为该时段内动车组最大整备数，也就是该时段动车所的通过能力。

因此，通过确定给定时段内满足动车所设备、作业规则和标准等时空资源的整备动车组数最多的动车所技术作业方案，即确定出给定时段内动车所时空资源利用率最大的动车所技术作业方案，即可得到动车所通过能力。

2 数学模型

整备动车组最多的动车所技术作业方案的确定需对动车组的接发顺序、接发进路、作业占用的股道、占用股道的起止时刻及作业间的转线进路等变量进行决策。下面基于这些决策变量，以整备动车组数最多为目标，给出满足各种约束的动车所通过能力计算模型。

2.1 优化目标

设动车所通过能力计算时段的开始时刻为TPs和结束时刻为TPe，本文模型的优化目标为在计算时段[TPs,TPe]内尽可能多的整备各种作业流程的动车组，实现动车组通过能力的最大化，即

( 1 )

式中:Z为处在各不同检修流程的动车组数量之和，列；ni为动车所办理的检修流程i的动车组数，列；M为动车组检修流程种类数(日常存车、一级检修、二级检修等)。

2.2 约束条件

(1) 动车所检修的动车组需要满足动车组检修流程类型比例约束

( 2 )

(2) 股道作业安排约束条件

每列动车组须满足场库股道时空占用的唯一性约束，即任意1条股道在任意时间内只允许1列动车组占用，表示为

( 3 )

( 4 )

( 5 )

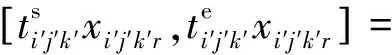
( 6 )

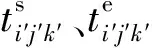
( 7 )

式( 3 )表示只能给每列动车组的每项作业安排1条股道；式( 4 )表示每列动车组被安排的股道数应不小于其检修流程所规定的作业数；式( 5 )表示每列动车组的每项作业在动车所股道上实际停留的时间应能够满足规定的最小作业检修时间；式( 6 )表示相继在同一条股道上到发的任意两列动车组，占用该股道的时间不允许冲突，即当某条股道已被某动车组占用时，不允许该股道再到发其他动车组；式( 7 )表示仅考虑作业时间在计算时段的动车组。

(3) 动车组检修作业顺序约束条件

每列动车组每项检修作业的开始、结束时刻必须满足其前项、后项作业时间的约束

( 8 )

( 9 )

式( 8 )中，当k=1时，表示第1项作业的开始时刻等于动车组入所时刻；当k≠1时，表示除第1项作业外，每项作业时间开始时刻都大于前一项作业结束时刻；当k=Di时，表示最后一项作业结束时刻必须等于动车组出所时刻；式( 9 )仅考虑出入所时刻在计算时段的动车组。

(4) 每列动车组每项检修作业的股道安排必须检修作业场库约束，即每项检修作业必须在特定的场库股道上完成，即

(10)

式中:Cijkr为检修流程为i的第j列动车组的第k个任务被安排在场库的股道r上进行作业的效益。当动车组按照动车所工作组织规定的安排在不能或不允许使用的股道r上时，Cijkr=0，否则Cijkr=1。

(5) 动车组进路安排约束条件

动车组须满足进路时空占用的唯一性约束，即任何1条进路在任意时间内只允许被1列动车组占用，为

(11)

(12)

式中:Iaa为检修流程为i的第j列动车组与前面检修流程为i′的第j′列动车组之间的最小到达间隔时间；Iad为检修流程为i的第j列动车组与前面检修流程为i′的第j′列动车组之间的最小到发间隔时间；Idd为检修流程为i的第j列动车组与前面检修流程为i′的第j′列动车组之间的最小出发间隔时间；Ida为检修流程为i的第j列动车组与前面检修流程为i′的第j′列动车组之间的最小发到间隔时间；pll′为0-1变量，如果进路l与l′存在冲突，则pll′=1，否则pll′=0。

(13)

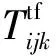
k≠1∪Dik′≠1∪Dipll′=1

(14)

式(11)表示只允许给每一动车组每项任务所在股道的转入、转出安排1条进路；式(12)表示不同动车组接发车进路占用冲突时必须要满足规定的最小间隔时间标准；式(13)表示动车组转线进路占用时间等于前后任务股道占用起止时间之差；式(14)表示不同动车组转线进路冲突时，要满足调车最小间隔时间标准。

3 算法设计

动车所通过能力计算中的决策变量和约束条件很多，技术作业方案数随着动车所设备规模、动车组数量的增加而呈现爆炸性增长，是NP难组合问题。若把动车组看作加工工件，动车组在动车所的每项检修或转线作业看作加工工序，每项检修或转线作业可选的股道或进路看作每道加工工序可以选择的多个平行机器，则动车所技术作业安排就是1个每个工件加工路径确定的多阶段混合流水车间调度问题[9-10]，而禁忌搜索算法是解决多阶段混合流水车间调度问题的有效算法之一。因此，针对动车所通过能力问题的特点，本文设计启发式排序规则[9]与基于最长活动链的混合邻域禁忌搜索算法[10]HNS-TS:Hybrid(Neighborhood Structure and Tabu Search)相结合的优化算法，进行模型的求解。由于直接求解动车所最大整备动车组数较为困难，算法中引入最晚动车组出所时刻这一优化指标。

3.1 优化指标设计

最晚动车组出所时刻是指某给定技术作业方案中最后1列出所动车的出发时刻。运用该指标可以方便的比较给定时间段内、检修运用任务相同的多个调车作业方案的优劣，该指标越小，表明对应的调车作业方案越好。因可以节省出更多的时空资源安排动车组作业，从而提高通过能力。

本文算法的思路为按检修类型比例生成1组动车组检修运用计划，然后在给定时段内为该计划生成最晚动车组出所时刻最小的调车作业方案，如果动车所通过能力有富裕，继续增加检修动车组并继续优化调车作业方案，直到通过能力用尽为止。

3.2 设计启发式排序规则生成初始方案

禁忌搜索算法对初始解依赖性较大，本文中通过设计启发式排序规则生成初始方案。启发式排序规则是根据动车所调车作业的长期实践经验、偏好性目标构建的一组动车组调车作业安排优先级的决策规则。遵循这些规则，逐个安排每列动车组的调车作业，可以构造出1个确定性的可行解。

(1) 动车组出入所时刻确定规则

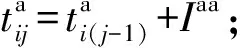
(2) 动车组出入所进路安排规则

遵循最大平行进路的规则为动车组安排到发进路。

(3) 动车组股道安排规则

由于动车组的某些设备资源具有稀缺性，如检修库、洗车库、不落轮镟轮临修等，应当减少动车组占用这些关键设备的无效时间。因此，遵循先到先排、关键设备所在股道紧凑使用、股道均衡使用规则安排动车组每项检修作业所在的股道。

(4) 动车组转线调车进路安排规则

遵循出场库调车进路优先入场库调车进路、最大平行进路优先的规则安排进路。

(5) 动车组股道占用时间规则

遵循最小作业时间标准规则。

(6) 动车组作业冲突解决规则

当动车组根据作业流程进行股道安排发生作业冲突时，需要调整作业起止时刻化解冲突。分为两种情况进行不同的操作:

① 动车组出入所发生接发进路冲突或存车线冲突时，需要比较所有与安排动车组进路冲突的列车，分别计算它们冲突化解需要满足的最小时间调整量，以其中最小值调整动车组的出入所时刻；

② 除出入所以外的其他作业发生转线进路或股道冲突时，需要延后该项作业的开始时刻，同时延长前一项作业的终止时刻，即在前一项作业中发生等待时间，该时间等于所有可用股道中腾空后能被利用的最小时间调整量。

图3的U3调车作业方案，从临修线转入检修线时通过设置等待时间，化解作业冲突。

生成动车所调车作业初始方案步骤:

Step1初始化动车所设备参数

各场库的股道、道岔及其联通关系，生成动车组进路联通表；初始化不同检修流程类型的动车组比例；初始化动车所不同检修流程所需的股道占用时间标准、到发间隔时间标准、转线进路时间标准；确定动车所通过能力计算的起止时间段等等；

Step2赋初值动车组总数n=0；

Step3生成1组符合不同作业流程类型的动车组比例的最小集合；

Step4是否集合中所有动车组均已安排计划，是则转Step3；否则，从现在的集合中随机选取一没有安排计划的动车组；

Step5根据“动车组出入所时刻确定规则”确定该动车组的出入所时刻；

Step6根据“动车组到发进路安排规则”、“动车组股道安排规则”，“动车组股道占用时间规则”、“动车组转线调车进路安排规则”，为该动车组安排作业所需的场库作业股道、到发进路、转线进路；如果该项作业找不到空闲的股道或进路，说明该动车组的作业安排与其他动车组发生冲突，转Step7，否则转Step8；

Step7根据“动车组作业冲突解决规则”调整该动车组作业起止时刻以及进路占用起止时刻，转Step6；

Step8若该动车组该项作业的终止时刻大于TPe，则将该项作业的终止时刻设为TPe，并转Step9；否则判断该动车组的所有作业项目是否都被安排了计划，是则记录该动车组，转Step4，否则转Step6；

Step9输出动车组总数，该值即为最大通过能力初始值，算法终止。

3.3 基于最长活动链的混合邻域禁忌搜索算法

运用启发式排序规则可以高效生成大规模调度问题的初始可行解，但不一定是最优解。由于每列动车组有多道作业工序，而加工工序的机器有限，因此将出现机器上工序排队现象，即每列动车组的工序间出现非生产等待时间，见图3，文献[10]已经证明工序加工整体作业时间是由最长关键加工路径时间决定的，如果要优化某调车作业方案的最晚动车组出所时刻，必须减少最长关键加工路径上的非生产等待时间，最长关键加工路径又称为最长活动链。

(1) 最长活动链的构造

为确定最长活动链，参考文献[10]给出相关概念：

① 工件的前沿工序:假设工序u和v是工件J的两个工序，在作业流程中，u需要在v前加工，则u就是v同一个工件的前沿工序，如果该两个工序恰好相邻，则u是v同一个工件的直接前沿工序；

② 机器上的前沿工序:设工序u和v是机器F上加工的两个工序，如果u的开始加工时间比v早，则称u是v的同一台机器的前沿工序，如果这两个工序恰好相邻，则u是v同1台机器的直接前沿工序；

③ 活动链:工序u1条活动链是1组工序的集合，开始于1个没有前沿工序的工序(即开始于第1道工序)，结束于工序u，活动链上的每个工序都是剩余工序中某块的工件直接前沿工序或机器直接前沿工序；

④ 活动链长度:活动链中第1个加工工序开始时刻至最后1个加工工序结束时刻的长度；

⑤ 最长活动链:所有活动链中，最晚加工完成的1个工序的活动链；

⑥ 活动块:最长活动链中，同1个机器加工的1组直接相邻工序的集合。

图3中，作业2是作业3的工件直接前沿工序、是作业5的工件前沿工序；作业3是作业4在洗车线上的直接前沿工序；作业1～3、作业5～9构成最长活动链，其时间是这7项作业时间之和；作业3、4和作业6、7都是最长活动链中的活动块。

最长活动链构造方法:

① 找到所有动车组中最后的作业工序RiF；

② 确定RiF的机器直接前沿工序和工件直接前沿工序，比较两个工序，选择结束时刻等于RiF的开始时刻的工序作为RiF的活动链直接前沿工序Ri(M-1)，继续查找Ri(M-1)的直接前沿工序，直到第1道作业Ri1为止，可得最长活动链；

③ 如果RiF的机器直接前沿工序和工件直接前沿工序的结束时刻相同，则可以任意选择或者指定选择其中之一为直接前沿工序。

(2) 基于最长活动链的混合邻域禁忌搜索算法

禁忌搜索算法的关键之一是在当前解的基础上构造出邻域解，然后通过优化指标、禁忌表、评价函数、终止条件等逐步搜索到最优解。

在本阶段算法中，通过确定当前调车作业方案中的最长活动链，然后移动或交换最长活动链上活动块内直接前沿工具有缓冲时间的作业，可形成1个新的可行调车作业方案，从而构造出邻域解。该方法能最大概率的减小最晚动车组出所时刻，有利于尽快搜索到最优解或满意解，见图3。作业7的直接前沿工序具有缓冲时间，因此可以交换作业6和作业7的检修顺序，得到1个新的安排计划，而交换作业3和作业4则不成立。

对禁忌搜索算法的主要参数进行设计:

① 初始解。运用启发式排序规则生成调车作业初始方案；

② 邻域结构。通过移动或交换当前最长活动链上的活动块上的动车作业产生邻域解；

③ 评价函数。最晚动车组出所时刻为邻域解的评价函数；

④ 禁忌表。针对发生的作业移动或交换进行禁忌，保证后面的迭代搜索不出现相同的移动情况。根据文献[10]的结论，HNS-TS算法采用所有工序数量的1/7为禁忌表长度是比较理想的，本文采用初始方案中的动车组总工序数量的1/7为禁忌长度；

⑤ 特赦条件。为避免丢失最优解，规定在找不到领域解及迭代一定次数后，特赦禁忌表中最优值为当前解继续进行迭代搜索；

⑥ 终止条件。设置最大迭代次数作为终止条件，或者最长活动链的活动块上以不能发生交换、移动等作业，则算法停止。

禁忌搜索算法优化方案具体步骤为:

Step1设迭代次数为1，将启发式排序算法初始方案置为当前方案；

Step3判断候选集解中对象是否满足藐视准则，选择邻域解中未被禁忌的对象或者满足藐视准则的禁忌对象为当前解，更新禁忌表；

Step4迭代次数增加1，若迭代次数为最大迭代次数或者解无法改进时，算法终止，输出最优方案，否则转Step2。

如果得到的优化方案中最晚动车组出发时刻小于终止时刻TPe，则继续按照3.2节算法增加动车组，直到最晚动车组出发时刻大于或等于终止时刻TPe时止，由此得到动车所通过能力。

4 算例验证

某动车所站场情况见图4。其中21G1～25G1、21G2～25G2暂时不开通使用。规定的最小车站间隔时间分别为列车到达追踪间隔4 min、列车出发追踪间隔3 min、列车不同时发到间隔时间8 min、列车不同时到发间隔时间3 min。动车组在动车所内各作业项目的最小时间标准见表1。日常主要有存车作业流程和一级检修流程2种，分别为到达动车所到发场—到发场存放动车组—发车；到达动车所到发场—洗车库洗车—库前场吸污、待检—检修库技检作业—到发场出库待发(存放)—发车。

假设动车所需要一级检修的动车组与存车作业的动车组的比例分别为40%、60%，动车组均为16辆编组，根据动车所历年数据统计，一级检修动车组到达或发车作业时间平均为30 min，存车整备作业动车组在动车所的整备作业时间平均为5 h。计算23:00～7:00之间的动车所通过能力。

表1 动车所各项作业时间标准

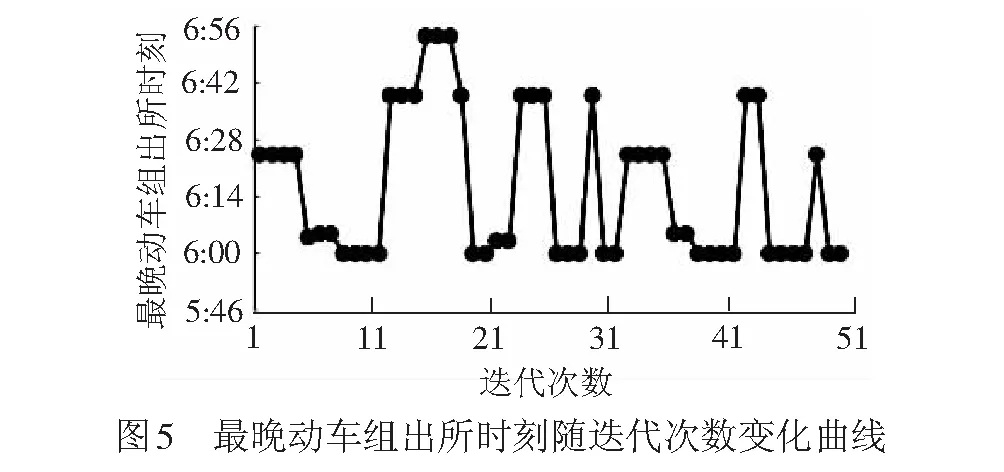
首先根据40%、60%的作业流程类型比例要求生成1组动车组集合。根据启发式排序规则安排每组动车组的作业计划，得到1个满足所有约束条件的动车调车作业初始方案，该初始方案的动车组数为14列，其中一级检修作业流程的动车组为6列，存车作业流程的动车组为8列，最晚动车组的出所时刻为6:25。然后构造第2阶段基于最长活动链的禁忌搜索算法对14列的初始方案进行优化，经过迭代50次后，得到优化方案，其中最晚动车组的出所时刻提早到6:00，见图5，表明初始方案给出的通过能力值偏小，可以利用优化方案中节省出来的时间继续增加动车组，最终得到动车组为20列，其中一级检修作业流程的动车组为8列，办理整备作业流程的动车组为12列，最晚动车组的出发时刻为6:30，最终结果见表2。作业安排结果显示，动车所洗车库和检修库是能力瓶颈所在，限制一级检修作业动车组的数量，而动车所到发场能力较为充足，如果不受到40%、60%的作业流程类型比例要求，还可以继续接发2列存车整备作业流程动车组，即通过能力增加到22列。

运用传统的利用率法仅能对一昼夜整备动车组数进行计算得到69列，取平均值则23:00～7:00按8 h计算约为23列，计算结果与上述优化算法相当，利用率法仅给出1个能力结果值，无法精确给出每组动车组设备利用和安排情况，而本优化算法生成最大通过能力下的调车作业计划，因此精确性及实用性更好。此外，有丰富经验的工作人员运用图解法安排并估计8 h内动车所最大通过能力值也为22列，也验证优化算法结果的正确性，但速度不及本优化算法。

5 结论

本文在建立满足各种约束条件的动车所通过能力整数规划模型后，提出启发式排序规则与基于最长活动链的混合邻域禁忌搜索算法相结合的优化算法，为模拟仿真法计算动车所通过能力提供思路，并以某实际动车所23:00～7:00时段通过能力计算为例，验证模型及算法的有效性，结果优于利用率法及图解法。但尚未考虑更多的实际情况，例如：实际作业时间呈现随机性变化，检修设备可以被多列动车组同时使用，动车组隔日开行等，将影响通过能力计算结果的实用性。下一步将对这些情况进行探讨，进一步提高计算方法的适用性。

参考文献：

[1] 杜文.旅客运输组织[M].北京：中国铁道出版社，2012：56-58.

[2] ALEX LANDEX. Capacity Statement for Railways[C]//Annual Transport Conference at Aalborg University. Denmark: Aalborg University ,2007:1-19.

[3] HAMED POURYOUSEF, PASI LAUTALA, THOMAS WHITE. Review of Capacity Measurement Methodologies:Similaritys and Differences in the U.S. and European Railroads[C]// Annual Meeting of the Transportation Research Board.USA: Transportation Research Board, 2013:1-14.

[4] 李波.动车所一、二级检修作业能力优化[J].中国铁路,2008(12):28-30.

LI Bo.Optimization of First-class and Second-class Maintenance Capability at EMU Depot[J].Chinese Railways,2008(12):28-30.

[5] 耿敬春,牛会想,肖春光,等.北京动车段出入段线建设规模及能力适应性分析[J].铁道工程学报,2008(10):74-77.

GENG Jingchun, NIU Huixiang, XIAO Chunguang, et al. Adaptablility Analysis of Scale and Capacity of the Entrance & Exit Depot Line of Beijing Multiple Unit Depot[J].Journal of Railway Engineering Society,2008(10):74-77.

[6] 林伯梁,张伟,王家喜.编制动车组一级修调车作业计划的启发式算法[EB/OL]. 北京:中国科技论文在线 [2013-12-16 ].http://www.paper.edu.cn/releasepaper/content/201312-375.

[7] 李建,林伯梁,王家喜.动车组日常检修计划优化调整决策支持系统[EB/OL]. 北京:中国科技论文在线 [2013-09-12].http://www.paper.edu.cn/releasepaper/content/201309-166.

[8] 王忠凯,史天运,张惟皎,等.动车运用所调车作业计划优化编制模型与算法[J].铁道学报,2013,35(8):1-9.

WANG Zhongkai, SHI Tianyun, ZHANG Weijiao,et al. Model and Algorithm for Optimized Formulation of Scheduled Shunting Operation Plans of Electric Multiple Units Depots[J].Journal of the China Railway Society,2013,35(8):1-9.

[9] 韦秋金.多阶段流水车间调度问题的启发式算法研究[D].沈阳：东北大学，2004:8-12.

[10] 邢德伟.加工车间调度问题中禁忌搜索算法的研究与改进[D].西安：西安电子科技大学，2010:19-32.