高速铁路板式无砟轨道不平顺下路基动应力的概率分布特征

陈仁朋， 江 朋， 段 翔， 蒋建群， 程 翀

(1.湖南大学 土木工程学院， 湖南 长沙 410082； 2. 浙江大学 软弱土与环境土工教育部重点实验室， 浙江 杭州 310058；3.浙江大学 建筑工程学院， 浙江 杭州 310058； 4.安徽省交通规划设计研究总院股份有限公司, 安徽 合肥 230088)

高速铁路路基动应力的分布特性是路基极限状态设计方法的基础[1]。除了列车速度、轴重等因素外，轨道不平顺是影响路基动应力分布特性的重要因素[2]。

目前，多数学者对路基动应力的研究都是基于确定性分析。Chen等[3]通过室内1∶1无砟轨道路基模型试验，对列车荷载作用下的路基动应力进行了研究，发现动应力沿路基深度的衰减曲线可用布氏解进行计算。陈建国等[4]建立车-轨-路基耦合动力学模型，研究了不同列车编组和行车速度条件下路基的动力响应，发现轴重对动应力的影响最为显著，列车速度对动应力也有一定的影响。范生波[5]对武广高速铁路及京津高速铁路开展了大量的现场试验，发现动应力在路基表面横断面呈马鞍状分布，列车轴重对路基动应力的影响最大。

路基动应力受到列车速度、轴重、轨道不平顺性等因素的影响，具有不确定性。刘扬[6]通过动力仿真软件建立了车-轨道结构模型，分客车和货车2种车体共18种工况，统计出轮轨动荷载在轨道不平顺下的变异系数为0.05～0.15，并通过验证发现其沿线路方向服从正态分布。武广高速铁路过渡段路基试验段进行的动态响应测试结果[1,7]表明基床表层面上的动应力幅值的变异系数范围为0.15～0.30。除此以外，路基动应力由于轨道不平顺导致的不确定性研究较少。

由于现场实测只能选取一些特定的位置，很难得到轨道不平顺下路基动应力的分布特性，因此理论研究非常重要。本文利用列车-板式轨道-路基三维动力有限元模型，开展了在德国低干扰谱下路基结构的动力响应分析，重点对高速列车不同运行速度下路基动应力沿线路方向进行概率统计，给出了动应力均值及变异系数沿路基深度方向的变化规律。通过柯尔莫哥洛夫检验方法，对路基动应力的正态性分布进行了检验。本文研究可为基于极限状态法的路基设计方法研究提供支撑。

1 列车-板式轨道-路基耦合作用三维动力有限元模型

采用ABAQUS有限元软件，建立了列车-板式轨道-路基的三维动力有限元模型，对板式轨道路基系统进行数值分析。

1.1 车辆模型

车辆模型主要有移动荷载模型、移动质量模型和移动悬挂质量模型。本文采用整车2系悬挂模型。建模时车体、转向架、轮对均为刚体结构；转向架与轮对之间由一系悬挂弹簧-阻尼系统连接，车体与转向架之间由二系悬挂弹簧-阻尼系统连接。2系悬挂模型能够考虑车身惯性、“点头”效应以及悬挂系统作用，较真实地反映在轨道不平顺情况下的列车动力行为。列车采用CRH3型车，参数值参考文献[8]，见表1。

表1 CRH3列车参数

1.2 轨道路基模型

板式轨道路基结构主要由钢轨、扣件、轨道板、CA砂浆层、混凝土底座、基床和地基组成。建模时，钢轨采用等截面、均质的I型直梁结构进行模拟，截面尺寸取UIC60标准断面尺寸。扣件系统采用弹簧阻尼系统进行模拟，支撑刚度取值为3×107N/m，阻尼取值为2.385×104N·s/m，扣件间距设为0.63 m，通过节点连接钢轨和轨道板。轨道板、CA砂浆层、混凝土底座、基床和地基部分采用8节点的实体单元模拟。由于路基受到的动静荷载相对较小，而路基的强度很高，因此本构模型选用线弹性模型，并根据结构特性设置杨氏模量、密度、泊松比等参数。相关各结构层之间(如轨道板和CA砂浆层之间)均采用绑定约束进行连接。板式轨道路基结构参数见表2。

表2 板式轨道路基结构参数

1.3 轮轨接触模型与轨道不平顺谱

轮轨接触关系是车辆与轨道结构耦合作用的基础，直接影响到轮轨力和计算的准确性。采用Penalty接触算法和有限滑移公式模拟轮轨之间的接触作用，并采用Hard接触[9]模拟轮轨之间的法向作用，可以较好地考虑轨道不平顺的影响。

轨道的垂向不平顺体现在钢轨表面，可使用三角级数法将已有的轨道不平顺谱转化为不平顺的空间分布，添加到钢轨表面的各单元节点坐标处。轮轨接触行为见图1。

轨道不平顺用三角级数法表示为

( 1 )

式中：u(x)为轨道不平顺样本序列；n为不平顺功率谱函数中的第n个取样点；N为总采样点数；wn为采样频率；φn为在[0,2π]上均匀分布的相互独立的随机变量；S(wn)为不平顺功率谱密度函数。

采用目前应用广泛的高速铁路轨道不平顺谱——德国低干扰谱。其高低不平顺密度函数为

( 2 )

式中：Sv(Ω) 为轨道谱，cm2/(rad/m)；Ω为空间角频率，rad/m；Ωr、Ωc为截断频率，rad/m；Av为粗糙度常数，m2·rad/m。

德国低干扰谱密度函数的特征参数[10]见表3。

表3 德国低干扰谱密度函数的特征参数

采用三角级数进行展开[11]，计算的不平顺空间分布见图2。

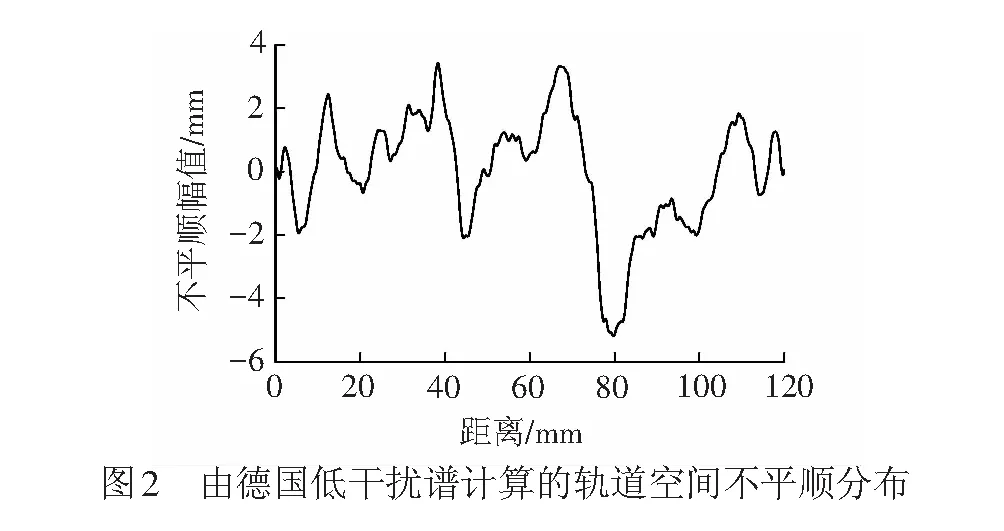
1.4 阻尼和边界设置

材料采用古典阻尼——瑞利阻尼[12]来表示，根据克拉夫的定义

C=a0m+a1k

( 3 )

式中：C、m、k分别为阻尼矩阵、质量矩阵和刚度矩阵；a0为质量比例阻尼；a1为刚度比例阻尼。

通常假设用于控制频率的阻尼比相同，即ξm=ξn=ξ。可以简化为

( 4 )

式中：ωm为系统基频；ωn在对路基系统动力反应有显著贡献的高阶阵型中选取，即可选定材料的阻尼。

对于动力学问题的数值模拟，要使用有限的空间高效地模拟半无限空间，边界选取十分重要。基于传统的边界处理方式上，参考文献[13]的方法建立递减阻尼边界模式，在本体结构外围设置逐层递增的边界，如图3所示，使得波动能量被逐渐吸收而不会在边界处产生反射。

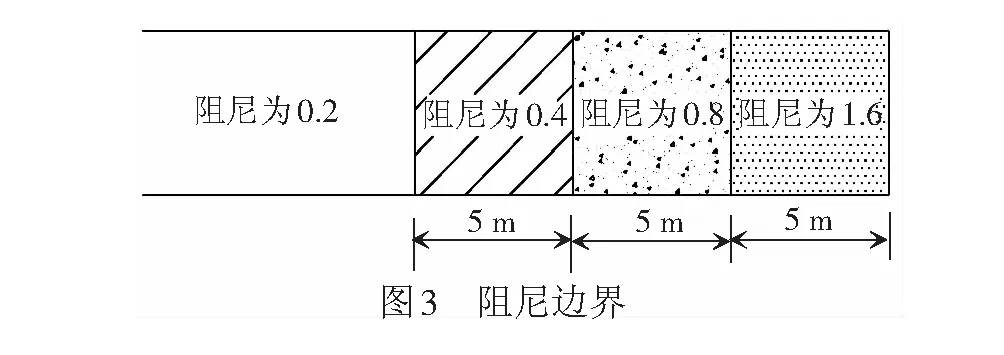
1.5 三维数值模型

为了统计路基动应力在轨道不平顺下沿线路方向的分布，建立无砟轨道路基数值模型，其断面见图4。采用4节车辆，为了提高计算效率初始时列车位于路基之外，路基系统分成3个区域，路基中间区域网格加密。翟婉明[14]提出，移动荷载作用下的车辆-轨道耦合模型中，轨道长度大于100 m之后，轨道结构的振动结果几乎不受影响，因此路基长取150 m。整个模型单元数目253 512个，节点数目为293 261。

2 轨道不平顺下路基动应力的概率统计及正态性检验

路基动应力是受多方面因素影响的，主要包括轨道不平顺、列车运行速度、轴重、轨道刚度等因素。这些因素的变化会导致路基动应力具有一定的随机性。其中，轨道不平顺性是导致路基动应力随机性的主要因素。根据板式轨道路基系统三维数值分析结果，对德国低干扰轨道不平顺谱下的路基动应力幅值进行了概率统计。

2.1 概率统计工况

沿深度方向选择了5个位置进行计算，见图5，分别是路基面中心点以下0.20、0.86、1.32、1.78、2.24 m。列车速度为350、250、150 km/h。分别统计3种列车速度下这5个位置处的路基动应力。

2.2 三维数值分析结果

列车不同速度、德国低干扰谱时，路基面中心下0.2 m处动应力的时程曲线见图6。图中：L为车厢长度，L=25 m;S2为车辆前后转向架中心距，S2=17.5 m;S3为相邻车辆前后转向架中心距，S3=7.5 m。可见，随着列车运行速度增大，轨道振动频率线性增大。当列车分别以速度350、250、150 km/h运行时，动应力幅值分别为21.46、16.62、14.48 kN。因此，列车速度对动应力幅值影响显著。

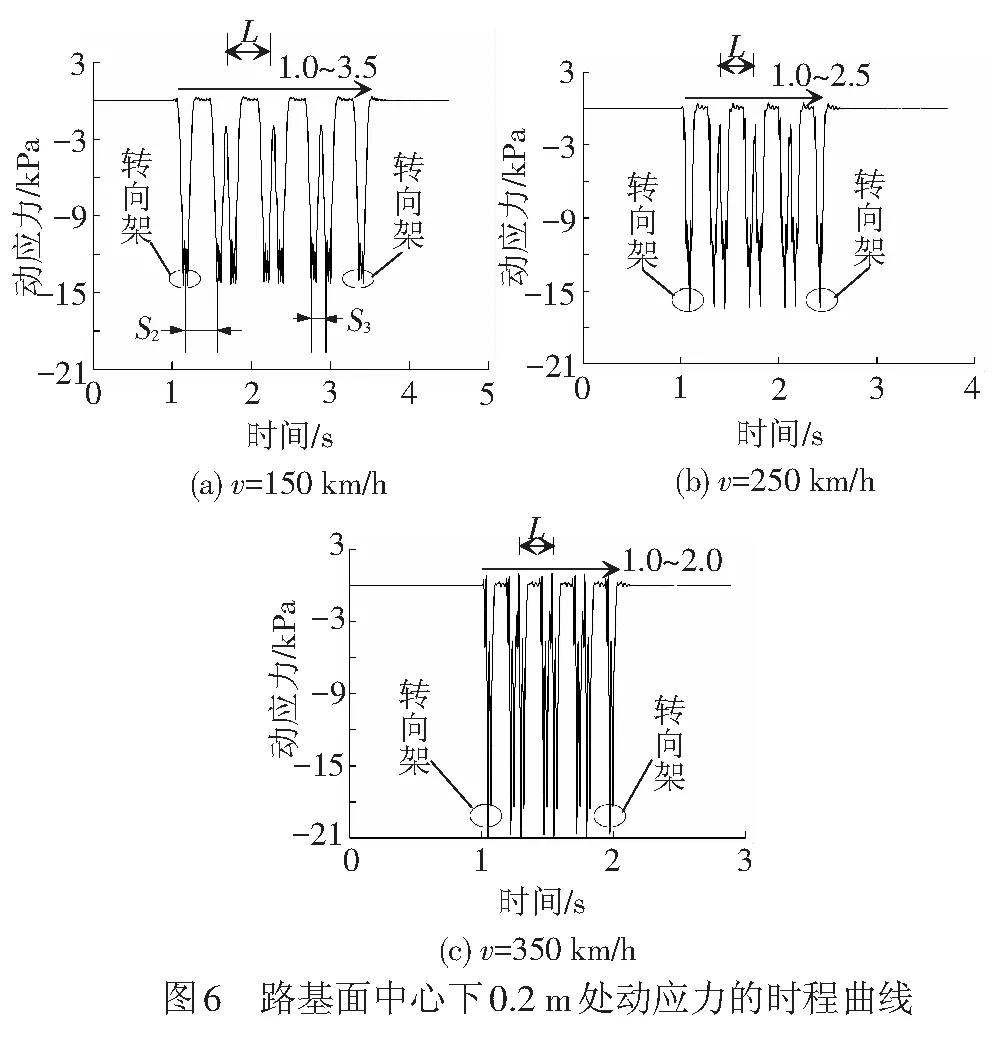
该模型路基面中心下0.2 m沿纵向共有272个节点，由于边界效应，去掉开始与结尾的各6个节点，取剩下260个节点每一个节点处的动应力幅值，得到动应力幅值沿纵向的分布曲线，见图7。明显可以看出，同一深度处的动应力幅值沿线路纵向是随机变化的，具有一定的离散性，且速度越大，离散性越明显。当列车速度为350 km/h时,路基动应力的分布范围达到了12.6～23.5 kPa，具有非常大的离散性。

2.3 路基动应力的概率统计

( 5 )

( 6 )

( 7 )

根据文献[7]，列车速度对路基动应力具有放大作用。为了消除列车速度对路基动应力统计的影响，引入动应力系数η，其表达式为

( 8 )

式中：σd为路基动应力；P0为列车轴重；v为列车运行速度;A为转向架中心距的1/2与轨道板宽度乘积。

根据有限元计算结果及式( 5 )～式( 8 )，得到动应力系数η的均值沿深度方向的分布，见图8。与布氏解结果[7]进行对比,发现在距离路基面0.5 m深度范围内，布氏解的衰减趋势比较快，在0.5 m深度范围外，二者的衰减趋势基本一致，说明了此数值模型的适用性。此外，在3种速度下路基动应力系数的均值沿深度的衰减曲线基本一致，并呈直线衰减。可见列车速度对路基动应力的影响与德国规范里采用的速度放大系数基本一致。此外，动应力系数的均值可用直线η=0.254h+1.106拟合。

由式( 5 )～式( 8 )对η的变异系数进行了统计，得到的结果见图9。可知，在德国低干扰谱下，η具有一定的变异性，且列车运行速度对η的变异系数影响非常明显。当列车分别以350、250、150 km/h运行时，路基动应力的变异系数分别为0.12～0.14、0.06～0.08、0.03～0.05,且沿深度方向都呈现出先增大后减小的趋势，在深度1.2 m处左右达到了最大值。由文献[1,7]可知，武广线过渡段(列车速度达到350 km/h)路基试验段η的变异系数为0.15～0.30。

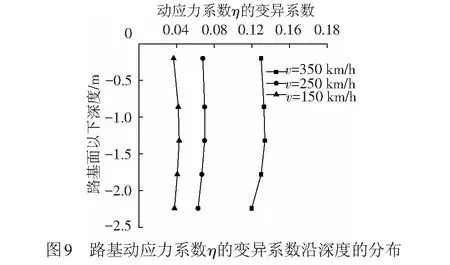
综上对路基动应力的概率统计结果可知，当列车提速时，路基动应力的均值和变异系数显著增加，对轨道路基的要求也会显著提高。

2.4 路基动应力的正态性检验

路基动应力的概率分布函数对路基累积变形的可靠度分析很重要。概率分布函数主要有正态分布函数、对数正态分布函数、Logistic分布指数分布、瑞利(Rayleigh)分布等。路基动应力的分布波形类似于正态分布。因此，需要研究路基动应力的分布特性，进行正态性检验。

正态分布是应用非常广泛的一种分布函数，其概率密度及分布函数分别为

( 9 )

(10)

正态性检验的方法有很多，包括χ2检验、柯尔莫哥洛夫检验和偏度峰值检验。本文采用柯尔莫哥洛夫检验方法[6],具体如下：

假定总体X的分布函数F(x)连续但未知，(X1,…,Xn)是取自这个总体的样本，并假定Fn(x)是F(x)的一种较优的估计，因此，取检验统计量

(11)

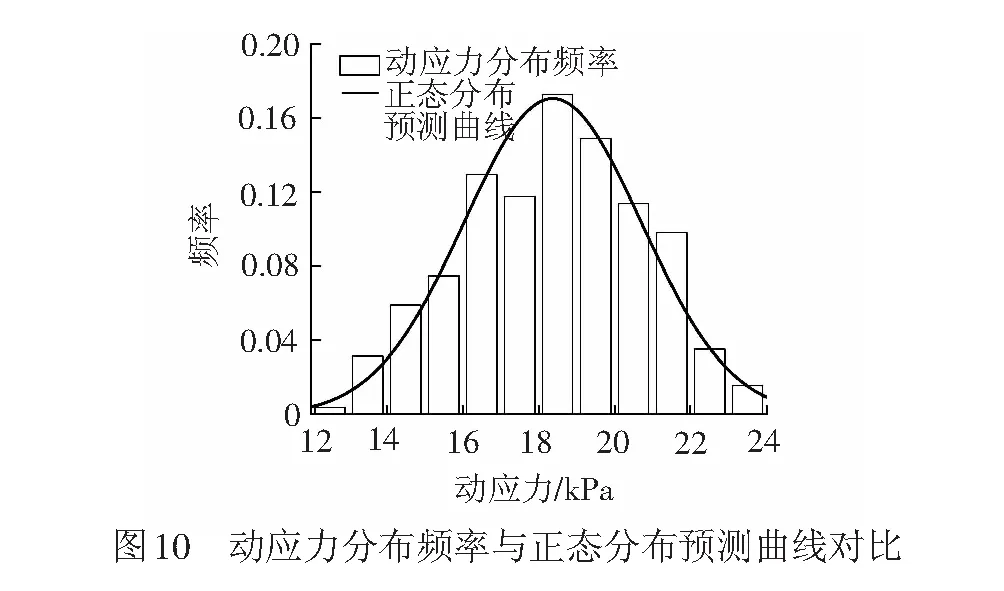
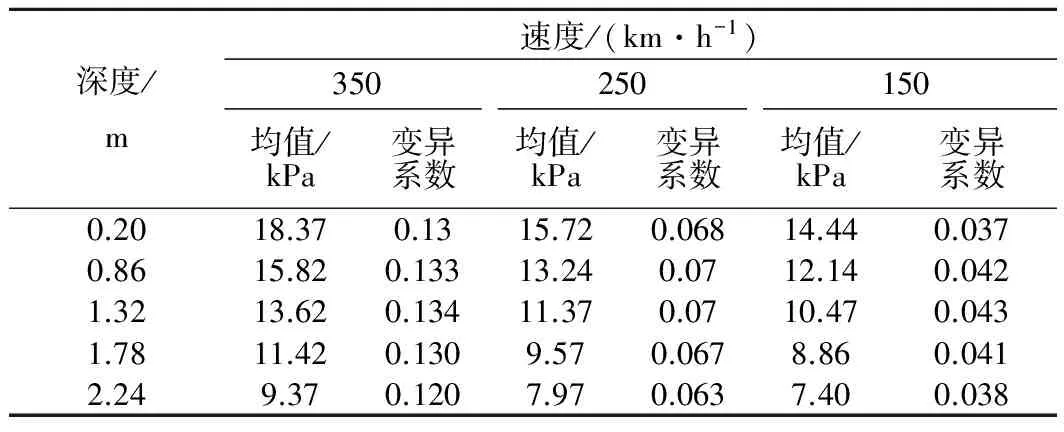
对于显著性水平α，取临界值Dn,α，当Dn

(12)

式中：(x1,…,xn)是次序统计量的观测值，

Fn(xi)=i/n

(13)

接下来检验动应力幅值是否符合正态分布，则

(14)

表4 路基动应力检验的观测值

由表4可以明显看出，在显著性水平α=0.01时，计算结果均小于临界值Dn,α。因此，列车以车速350、250、150 km/h运行时，各个路基深度处的动应力幅值均服从正态分布。列车速度为350 km/h时路基面下0.2 m处的动应力沿纵向的统计频率与正态分布预测曲线的对比见图10。

综上，高速铁路轨道不平顺下路基动应力服从正态分布，其均值和变异系数见表5。因此，可以得到轨道不平顺下路基动应力的概率分布特性。

表5 路基动应力的统计参数

深度/m速度/(km·h-1)350250150均值/kPa变异系数均值/kPa变异系数均值/kPa变异系数0．2018．370．1315．720．06814．440．0370．8615．820．13313．240．0712．140．0421．3213．620．13411．370．0710．470．0431．7811．420．1309．570．0678．860．0412．249．370．1207．970．0637．400．038

3 结论

本文在列车-板式轨道-路基三维有限元动力耦合模型的基础上，建立了高速铁路双线路基模型，对板式轨道路基系统在典型轨道不平顺谱——德国低干扰谱及350、250、150 km/h 3种典型速度工况下路基的动应力沿路基纵向及深度方向的分布进行了分析，统计路基动应力幅值的均值及变异系数，并采用柯尔莫哥洛夫检验方法对路基动应力幅值的正态性进行了验证。得出以下结论:

(1) 列车在3种速度下，路基动应力的均值沿路基深度方向基本都呈现直线衰减，随着列车速度的增加，动应力的均值会明显增加。

(2) 在德国低干扰不平顺谱下，路基动应力沿纵向具有一定的变异性，车速越高变异性越大；当车速为350 km/h时动应力的变异系数达到0.13～0.14。

(3) 列车以3种典型速度运行时，各个路基深度处的动应力均服从正态分布。

参考文献：

[1] CHEN Renpeng, JIANG Peng, YE Xiaowei, et al. Probabilistic Analytical Model for Settlement Risk Assessment of High-speed Railway Subgrade[J]. Journal of Performance of Constructed Facilities, ASCE, 2016，30(3):1-10.

[2] 陈仁朋, 王作洲, 蒋红光, 等. Ⅰ型轨道-路基系统动力荷载放大系数模型试验研究[J]. 岩土力学, 2013, 34(4): 4-8.

CHEN Renpeng, WANG Zuozhou, JIANG Hongguang, et al. Experimental Study of Dynamic Load Magnification Factor for Type Ⅰ Track-subgrade System[J]. Rock and Soil Mechanics, 2013, 34(4):4-8.

[3] CHEN Renpeng, CHEN Jinmiao, ZHAO Xing, et al. Cumulative Settlement of Track Subgrade in High-speed Railway Under Varying Water Levels[J]. International Journal of Rail Transportation, 2014,2(4): 205-220.

[4] 陈建国, 肖军华， 李前进， 等.提速列车荷载作用下铁路路基动力特性的研究[J].岩土力学, 2009,30(7): 1 944-1 950.

CHEN Jianguo, XIAO Junhua, LI Qianjin, et al.Dynamic Responses of Existing-railway Subgrade with Train Speed Increasing[J]. Rock and Soil Mechanics, 2009,30(7): 1 944-1 950.

[5] 范生波. 高速铁路无砟轨道动响应测试分析[D]. 成都：西南交通大学,2010.

[6] 刘扬. 有砟轨道沉降的概率预测模型[D]. 上海：同济大学，2007.

[7] 陈仁朋, 江朋, 叶肖伟, 等. 高铁单线路基循环累积变形分析方法及其可靠度分析[J]. 岩石力学与工程学报,2016,35(1):141-149.

CHEN Renpeng, JIANG Peng, YE Xiaowei, et al. Analysis Approach and Reliability Analysis of Cyclic Cumulative Deformation of High-speed Railway Single Subgrade[J]. Journal of Rock Mechanics and Engineering, 2016,35(1):141-149.

[8] 刘学毅. 客运专线无砟轨道设计理论与方法[M].成都： 西南交通大学出版社, 2010.

[9] 张斌, 雷晓燕. 基于车辆-轨道单位的无砟轨道动力特性有限元分析[J]. 铁道学报, 2011,33(7): 78-85.

ZHANG Bin, LEI Xiaoyan. Analysis on Dynamic Behavior of Ballastless Track Based on Vehicle Elements with Finite Element Method[J].Journal of the China Railway Society, 2011, 33(7): 78-85.

[10] PARK K C. An Improved Stiffly Stable Method for Direct Integration of Nonlinear Structual Dynamic Equations[J]. Journal of Applied Mechanic, 1975, 42(2): 446-470.

[11] 程翀. 车-轨-路耦合条件下的高速铁路板式轨道路基系统动力分析[D]. 杭州： 浙江大学, 2015.

[12] LEI Xiaoyan, ZHANG Bin. Analysis of Dynamic Behavior for Slab Track of High-speed Railway Based on Vehicle and Track Elements[J]. Journal of Transportation Engineering, 2011,137(4):227-240.

[13] LIU G R, QUEK JERRY S S. A Non-reflecting Boundary for Analyzing Wave Propagation Using the Finite Element Method [J]. Finite Elements in Analysis and Design, 2003, 39(5): 403-417.

[14] 翟婉明. 车辆-轨道耦合动力学[M].北京：科学出版社, 2007.